考慮導線模型與孤立檔計算的架空輸電線路設計

［關鍵詞］架空輸電線路；導線模型；孤立檔；電力系統

架空輸電線路設計的科學性直接關系到整個輸電系統的穩定性與經濟性。受氣象條件、地理環境以及地質等因素的影響，在對架空輸電線路進行設計的過程中必須考慮導線模型的建立與孤立檔的計算。導線模型不僅關系到線路的力學性能和電磁性能，而且對輸電線路的安全性和經濟性有著直接影響。孤立檔計算則涉及導線在不同氣象條件下的動態行為，對于線路能否在極端氣候下安全運行十分重要。

為了提高輸電系統的性能，提出一種基于導線模型和孤立檔計算的架空輸電線路設計方法，期望通過該方法促進電力系統朝著安全、高效的方向發展。

1 基于導線模型的架空輸電線路設計

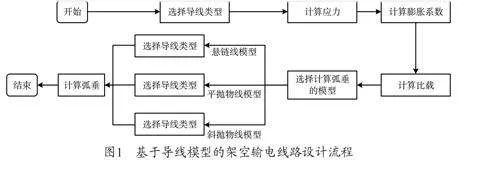
在架空輸電線路設計中，可供選擇的導線類型較多，包括傳統的鍍鋅鋼絞線、鋁包鋼絞線，以及新型的碳纖維復合芯鋁絞線和鋼芯耐熱鋁合金絞線等。不同導線模型的輸電線路設計計算方法不同。鑒于鋼芯耐熱鋁合金絞線在耐高溫、抗腐蝕等方面的優異表現，研究選擇其進行計算。該導線通過兩根不同的單股線絞合而成，電阻較低，且導線整體性能較好。兩根導線絞合后，由于兩者之間聯系緊密，沒有產生相對滑動，則絞線整體的力學參數不變。首先計算出絞線各部分的應變，計算方法如下式所示。

式中，φS為絞合線中鋼芯的應變，TS為鋼芯受到的拉力，ES為鋼芯的彈性系數，AS為鋼芯的面積，φA為絞合線中鋁合金的應變，TA為鋁合金受到的拉力，EA為鋁合金的彈性系數，AA為鋁合金的面積，φD為導線受到的拉力，TD為絞合線中導線的應變，ED為導線的彈性系數，AD為導線的面積。

其中，拉力單位為N，彈性系數的單位為Gpa，膨脹系數的單位為1/℃。由于絞線各部分的參數相等，則能夠計算出絞線的彈性系數，計算方法如下式所示。

在鋼芯耐熱鋁合金絞線中，鋼芯位于絞線內部，而鋁合金位于絞線外部，鋼絲受熱會變長，鋁絲受熱則會變短，從而可以計算出導線的熱膨脹系數，計算方法如下式所示。

式中，αD為導線的熱膨脹系數，αS為鋼絲的熱膨脹系數，αA為鋁合金的熱膨脹系數。

計算導線的應力與比載，應力一般取輸電線路最低點應力。比載即導線受到的機械荷載，主要包括7種，計算方法如下式所示。

式中，η1為導線的自重比載，N/m·mm2；g為重力加速度；m0為單位導線的質量，kg/km；s為導線的橫截面積，mm2；η2為導線的冰重比載，N/m·mm2；ρ為冰的密度；b為覆冰厚度，mm；d為導線的直徑，mm；η3為導線自重與冰重總比載，N/m·mm2；η4為無冰時的風壓比載，N/m·mm2；C為風載體系數；a為風速不均勻系數；η5為覆冰風壓比載；η6為無冰有風總比載；η7為有冰有風總比載。

導線的弧垂也是需要精確計算的重要參數，其值過大或過小都會對導線的應力產生影響，從而影響整個線路。通常采用懸鏈線模型、平拋物線模型以及斜拋物線模型3種模型計算弧垂，其中懸鏈線模型比較復雜，平拋物線模型誤差較大，而斜拋物線模型復雜度低，且計算準確率高。因此，研究使用斜拋物線模型計算弧垂。計算方法如下式所示。

式中，fm為架空線檔中弧垂最大值；η為架空線垂直比載；l為水平檔距；σ0為最低點應力，β代表拋物線與水平軸之間的夾角；f為架空線當中任意一點的弧垂；x為拋物線上任意一點的橫坐標。

基于導線模型的架空輸電線路設計流程如圖1所示。

2 基于孤立檔計算的弧垂與相間距離校準技術

盡管通過導線模型已經能夠計算出架空輸電線路設計中的各項參數，但在架空輸電線路的運行過程中，氣象條件是一直發生變化的。氣象條件的變化會對導線的應力和弧垂產生影響，在計算弧垂時，還需要考慮氣象條件的影響。在實際架空線路設計工程中，普遍遇到的都是連續檔的情況，當氣象條件改變時，連續檔的檔距與應力都會發生變化，計算過程較為復雜。孤立檔的檔距是確定的，僅有應力變化，故研究基于孤立檔控制計算弧垂。首先計算拋物線兩端點的力矩方程，如下式所示。

最后即可計算出不同情況下，導線的檔內最大弧垂，具體計算方法如下式所示。

式中，fm為當一側有絕緣子，沒有集中荷載時的檔內最大弧垂；為當兩側均有絕緣子，沒有集中荷載時的檔內最大弧垂；為當兩側均有絕緣子，有集中荷載時的最大弧垂；ηs為耐張絕緣子串的比載，N/m·mm2；λ0為耐張絕緣子串的長度，mm。

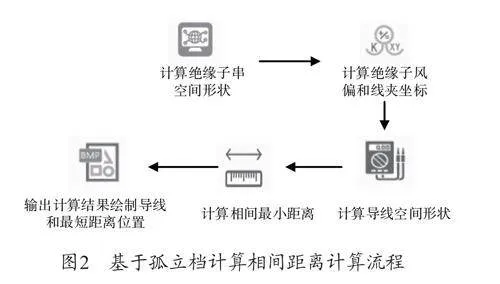
通過孤立檔計算出導線的各項參數后，即可確定導線的形狀。還需計算出孤立檔的相間距離，以確定導線的三維空間形狀。相間距離計算流程圖如圖2所示。

圖2中，首先計算出絕緣子串的空間形狀，在絕緣子串中，由于組成絕緣子串的各個部分均較短，同時，其荷載決定于絕緣子串的長度，因此，可將其看為一個多個部分絞合而成的模型。接著在由絕緣子串構成的架空線進線檔中，假設架空輸電線路的比載呈均勻分布，這時，將導線自重的荷載在水平方向上表示，具體計算方法如下式所示。

式中，p0為導線自重的荷載在水平方向上的集中程度，Q為架空輸電線路導線的總截面積，z為進檔線兩端的連線與水平方向的夾角。

根據架空輸電線路中某一點到端點的水平距離、該點弧垂、比載等參數獲得導線的二維空間形狀，使用的方程式為斜拋物線公式，同時，由于架空輸電線路處于三維空間中，并且在計算時還會受到風偏的影響。因此，研究最后將得到的導線二維空間形狀轉換為三維空間，計算方法如下式所示。

式中，（X1，Y1，Z1）為架空輸電線路中某一點的坐標，（X'，Y'，Z'）為三維空間時該點的坐標，θ為架空輸電線路的風偏角，κ為三維空間中的X與二維空間中高度軸的夾角。

至此，根據獲得的導線的三維空間形狀，即可進行架空輸電線路的設計。

3 架空輸電線路設計方法實例分析

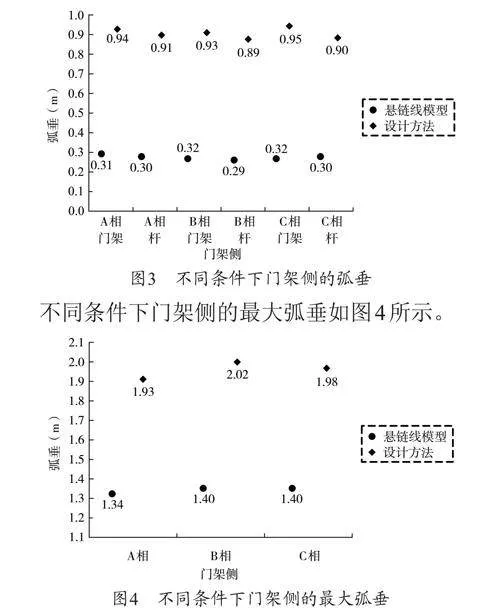
為驗證設計的基于導線模型和孤立檔計算的架空輸電線路設計方法的效果，以某220kV架空線路入地改造工程為例，該工程中，每根導線張力的最大值為10kN，門架上懸掛點之間的距離為4m，耐張絕緣子串的長度均為3.99m。架空輸電線路門架包括A相門架側、B相門架側、C相門架側，A相桿側、B相桿側、C相桿側。首先計算出設計方法與基于懸鏈線模型的方法所有門架側進線檔的弧垂與最大弧垂，不同條件下門架側的弧垂如圖3所示。

綜合圖3和圖4，可以發現，設計的基于導線模型和孤立檔計算的架空輸電線路設計方法的弧垂明顯高于傳統方法的弧垂，證明了該方法能夠有效提升架空輸電線路的安全性。

4 結束語

隨著電力工業的不斷發展，架空輸電線路作為電能傳輸的重要方式，其安全性受到了諸多關注。為了確保架空輸電線路的穩定，設計一種基于導線模型與孤立檔計算的架空輸電線路方法。結果顯示，使用該設計方法后，A相、B相以及C相的進檔線最大弧垂分別為1.93m、2.02m、1.98m，顯著高于使用基于懸鏈線模型的方法，證明了設計方法的有效性。然而，研究還存在未對多種導線進行對比的不足之處，后續會將設計方法應用于多種導線，以提升方法的適用性。