融合差分教學優化的粗糙集屬性約簡算法

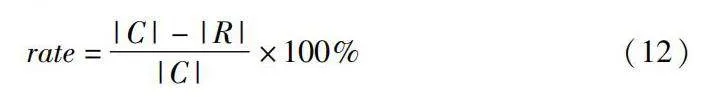
摘 要：針對傳統粗糙集理論在屬性約簡中存在計算復雜度高、易陷入局部最優解等問題，結合差分教學優化算法的全局搜索能力和粗糙集在處理不精確和不確定數據方面的優勢，提出融合差分教學優化的粗糙集屬性約簡算法（rough set attribute reduction algorithm based on differential teaching-learning optimization，AR-DTLBO）。首先，引入自適應教學因子和差分變異策略對教學優化算法進行改進，提高算法的搜索能力和優化性能；其次，通過改進后的教學優化算法“教”和“學”兩個階段對屬性約簡過程進行優化，降低了數據集的維度和復雜性；最后，在UCI數據庫中的8個數據集上將所提算法和其他六種算法進行對比實驗。實驗結果表明，該算法在約簡長度、約簡時間、約簡率和分類精度上均取得了良好的效果，實現了對數據集的有效約簡和優化，能夠有效減少冗余信息并提高決策規則的準確性，為決策分析和數據挖掘等領域提供了有效支撐。

關鍵詞：教學優化算法；教學階段；學習階段；差分變異策略；屬性約簡

中圖分類號：TP18 文獻標志碼：A 文章編號：1001-3695（2024）11-016-3317-06

doi：10.19734/j.issn.1001-3695.2024.04.0102

Rough set attribute reduction algorithm based on differential teaching-learning optimization

Zhou Wanting， Zheng Yingchun^?， Wei Botao

（School of Science， Xi’an University of Science amp; Technology， Xi’an 710054， China）

Abstract：To address the challenges of high computational complexity and the tendency to get stuck in local optima during attribute reduction within traditional rough set theory， this paper proposed an innovative rough set attribute reduction algorithm based on differential teaching-learning optimization （AR-DTLBO）. Leveraging the global search capabilities of the differential teaching-learning optimization algorithm along with the strengths of rough set theory in handling imprecise and uncertain data， the algorithm aimed to optimize the process. Firstly， it enhanced the teaching-learning optimization algorithm by introducing an adaptive teaching factor and a differential mutation strategy， thereby enhancing its search capabilities and optimization perfor-mance. Subsequently， it refined the attribute reduction process through the improved teaching-learning optimization algorithm’s “teaching” and “learning” phases， effectively reducing the dimensionality and complexity of datasets. Finally， it conducted comparative experiments between the proposed AR-DTLBO algorithm and six other algorithms， using eight datasets from the UCI database. The experimental results demonstrate that the proposed algorithm achieves favorable outcomes in terms of reduction length， reduction time， reduction rate， and classification accuracy. This successful reduction and optimization of datasets not only reduces redundant information but also enhances the precision of decision rules. These findings provide valuable support for decision analysis， data mining， and other related fields.

Key words：teaching optimization algorithm; teaching stage; learning stage; differential mutation strategy; attribute reduction

0 引言

粗糙集理論由Pawlak^［1］于1982年提出，用于處理不確定性和不完全數據的數學工具，能夠有效地分析和處理數據中的冗余和噪聲。屬性約簡是粗糙集理論中的一個重要研究方向，通過減少數據集中的屬性數量，簡化數據處理過程，提高處理效率。Muhammad等人^［2］研究了基于粗糙集的屬性約簡算法，提出基于啟發式的依賴算法，提高了約簡速度。Wang等人^［3］針對模糊粗糙集，設計了一種基于貪婪收斂策略的屬性約簡算法。張敏等人^［4］研究了鄰域粗糙集屬性約簡算法，提出了一種基于加權鄰域依賴度的屬性約簡算法。景運革等人^［5］研究了增量式屬性約簡，提出一種基于屬性值和屬性變化的增量式屬性約簡算法。傳統的依賴度和關聯規則方法更側重于統計或規則挖掘的方式來評估屬性的重要性，更適用于靜態或變化較慢的數據集，且隨著數據規模的增大面臨更高的計算復雜度；當決策表的維數不斷增大時，時間復雜度也隨之逐步上升。因此，降低時間復雜度、減少計算量成為研究的重點，旨在提升算法效率。

為提高屬性約簡算法的效率，有學者提出將傳統智能算法與屬性約簡相結合。吳尚智等人^［6］將粗糙集與蟻群算法相結合，使其在信息素更新規則和解決方案構建中快速找到最優解；欒雨雨等人^［7］將混沌離散粒子群與粗糙集相結合，實驗結果表明，該方法能夠約簡更多的條件屬性，提高分類精度；Chen等人^［8］提出基于改進魚群算法的鄰域粗糙集屬性約簡算法，結果表明該方法屬性約簡個數少；白建川等人^［9］將新型灰狼優化算法應用于粗糙集屬性約簡技術，經對比實驗驗證，該方法可行有效，不僅約簡結果精簡，而且識別準確率高，具有重要的理論價值和實踐意義；Mohamed等人^［10］提出改進社會蜘蛛優化算法求解粗糙集的最小屬性約簡問題。雖然傳統智能優化算法與屬性約簡相結合取得了一定的成果，但在處理大規模數據集或復雜問題時，仍面臨計算量大、效率低的挑戰，且在處理數據復雜性方面仍存在局限性。教學優化算法（teaching-learning optimization algorithm， TLBO）由印度學者Rao等人^［11］于2011年提出，該算法的原理是模擬現實班級中的教學現象，該算法具有結構簡單、實現容易、參數設置少、收斂穩定、算法精度高等優點。其成功應用于現實問題中如工業工程的應用問題^［13］、移動機器人路徑規劃問題^［14］、云優化算法的動態資源分配問題^［15］、車間調度問題^［16］。

TLBO算法結合了群體智能和個體學習的特點。將自適應教學因子和差分變異策略引入TLBO算法，能夠更好地適應問題的復雜性和多樣性，動態調整搜索策略和參數，優化搜索路徑，避免陷入局部最優解，使得在處理大規模或復雜數據時更加高效和準確^［17］，增加了種群的多樣性。而在粗糙集屬性約簡問題中，目的是尋找最小條件屬性子集，使得數據系統的分類能力保持不變，需要一種能夠靈活調整、具有較強的全局搜索能力和局部優化能力的算法。差分教學優化算法和粗糙集屬性約簡算法具有目標一致性、搜索策略相似和問題復雜性相似，通過差分策略可以實現屬性的動態調整，從而更好地適應屬性約簡問題，因此本文提出融合差分教學優化的粗糙集屬性約簡算法（AR-DTLBO）。通過UCI數據庫與傳統屬性約簡算法進行仿真對比實驗，AR-DTLBO算法相對于傳統智能優化算法，在處理粗糙集屬性約簡問題時有更好的性能和效果，在效率和速度上具有優勢，且適用于處理大規模或實時性要求較高的數據。

1 粗糙集理論

在粗糙集理論中，知識表達系統定義為S=〈U，R，V，f〉，U為論域，R=C∪D為屬性集合，C為條件屬性集，D為決策屬性集；V=∪r∈RV_r為屬性值集合（V_r為屬性r的值域）；f：U×R→V為一個映射函數，通過f可以確定U中每一個對象x_i的屬性值。

定義1^［1］ 設U是論域，P是U上的一個等價關系。U/P表示P的所有等價類（或U上的分類）構成的集合，［x］_p表示包含元素x∈U的P等價類。一個知識庫就是一個關系系統K={U，P}，其中P是U上的等價關系簇。設論域U上的一個等價關系簇為Q，若Q∈P且Q≠，則∩Q仍是論域U上的一個等價關系，稱為Q上的一個不可分辨關系，記為IND（Q）。

對于信息表I（U，A），若存在屬性集B∈A，且滿足IND（B）=IND（A），則稱B是A的一個約簡。

定義2^［1］ 對于論域U中的每個子集XU，根據不可分辨關系IND（Q），則集合X的下近似Q（X）和上近似Q（X）定義如下：

定義3^［1］ 在信息系統S=〈U，R，V，f〉中，對于每個子集XU，X的Q正域、Q負域、Q邊界域定義如下：

POS_Q（X）=Q（X）

NEG_Q（X）=U－Q（X）

BNG_Q（X）=Q（X）－Q（X）

定義4^［1］ 在信息系統S=〈U，R，V，f〉，（R=C∪D）中，條件屬性子集B∈C和決策屬性子集D之間的依賴度定義如下：

γ_B（D）=|POS_B（D）||U|（1）

若γ_B（D）=0，則D獨立于B；若γ_B（D）=1，則D完全依賴于B；若0lt;γ_B（D）lt;1，則D部分依賴于B。

定義5^［1］ 在一個信息系統S=〈U，R，V，f〉中任意a∈C，γ（C/{a}，D）為C中刪除條件屬性a后，其與決策屬性集D之間的依賴關系將發生變化，定義屬性a的重要度：

SGF（a，C，D）=γ（C，D）－γ（C/{a}，D）γ（C，D）=1－γ（C/{a}，D）γ（C，D）（2）

2 教學優化算法

教學優化算法^［11］是模擬現實班級中的教學現象，分為“教”和“學”，在算法中學生學習的科目代表種群的維度，班級中學生的數量代表種群的規模，教師被定義為班級中成績最優秀的學生，學生的學習成績相當于適應度值。具體分為以下三個步驟。

2.1 初始化班級

假設班級中學生的總數為n，學生學習的科目為d，初始化種群按式（3）生成：

X_M=Min_X+rand（Max_X－Min_X）（3）

其中：M=1，2，…，n；X_M表示班級中第M名學生；rand函數表示取［0，1］的隨機數；Min_X和Max_X分別代表X在解空間中取到的最小值和最大值。

2.2 教學階段

在實際教學過程中，學生根據班級平均水平與教師之間的差異進行學習。第i次迭代過程中，第M名學生在第j門學科與教師之間的差距如下：

Difference_{i， j，M}=rand（X_{i， j，MBest}－T×Mean_{i， j}）（4）

其中：X_{i， j，MBest}表示班級中最優秀的學生；T=round［1+rand（0，1）］表示教學因子；Mean_{i， j}=∑nM=1X_{i， j，M}/n表示班級學生在第i次迭代過程中第j門課程的平均水平；round函數表示四舍五入取整，對班級中第M名學生根據式（5）進行更新：

X¹_{i， j，M}=X⁰_{i， j，M}+Difference_{i， j，M}（5）

其中：X⁰_{i， j，M}和X¹_{i， j，M}表示第i次迭代過程中第M名學生在第j門課程學習前后的知識水平，若f（X¹_{i， j，M}）gt;f（X⁰_{i， j，M}），則更新f（X⁰_{i， j，M}），否則不進行更新。

2.3 學習階段

在現實教學中，學生不僅向教師學習，還可以通過學生之間的相互學習來提高自己的成績。在這一階段中，隨機選擇兩名互異的學生M₁、M₂，在第i次迭代過程中產生新的學生公式如下：

X²_i，M1=

X⁰_i，M1+rand（X⁰_i，M1－X_i，M2）， f（X⁰_i，M1）gt;f（X_i.M2）

X⁰_i，M1+rand（X_i，M2－X⁰_i，M1）， f（X⁰_i，M1）lt;f（X_i.M2）（6）

其中： f（X_i，M）表示每名學生的適應度值。若f（X²_i，M1）優于f（X⁰_i，M1），則進行更新，否則不進行更新。

3 改進后的差分變異教學優化算法

根據實際教學過程，對教學優化算法進行改進。首先更新教學因子，其次將差分進化算法中的變異策略應用到教學階段和學習階段。既保持了原始算法的特點，又增強了全局搜索能力。

3.1 自適應的教學因子

在教學優化算法中，教學因子取值僅限于1或2，這反映了學生從教師那里要么未能學到知識，要么學到了一定程度的知識，或者學到了全部的知識。但在實際教學中學生所學到的知識一般都是介于1和2之間，因此對教學因子進行如下改進：

T_new=T_max－iI_max（7）

其中：T_max表示教學因子的最大值；I_max表示最大迭代次數；i表示當前迭代次數。開始教學因子的取值為2，學習難度較小，學生的接受能力強。隨著迭代次數的增加，教學因子由2逐漸趨近于1，則當學習難度不斷增加，學生的接受能力不斷降低。

3.2 差分變異優化算法

差分進化算法是一種優化算法，它依賴于群體智能來實現，通過模擬自然界的進化過程來解決優化問題。差分進化算法在搜索空間中進行迭代搜索，通過變異、交叉和選擇等操作不斷進化種群，從而找到問題的最優解^［18］。

3.2.1 教學階段的改進

在教學階段，學生根據班級平均水平與教師之間的差異進行學習。第i次迭代過程中，第M名學生在第j門學科的學習水平若高于班級平均水平，則根據自身與教師之間的差異進行學習；第i次迭代過程中，第M名學生在第j門學科的學習水平低于班級平均水平，則根據教師與班級平均水平的差異進行學習。因此對教學階段改進如下：

Difference^new_{i， j，M}=rand（X_{i， j，MBest}-T_newX⁰_{i， j，M}） f （X⁰_{i， j，M}）gt;f（Mean_{i， j}）

rand（X_{i， j，MBest}-T_newMean_{i， j}）f （X⁰_{i， j，M}）lt;f（Mean_{i， j}）（8）

其中：X_{i， j，MBest}表示班級中最優秀的學生；T_new代表改進后的教學因子。對班級中第M名學生根據式（9）進行更新：

X¹_{i， j，M}=X⁰_{i， j，M}+Diffence^new_{i， j，M}（9）

其中：X⁰_{i， j，M}和X¹_{i， j，M}代表第i次迭代過程中第M名學生在第j門課程學習前后的知識水平，若f（X¹_{i， j，M}）gt;f（X⁰_{i， j，M}），則更新f（X⁰_{i， j，M}），否則不進行更新。

3.2.2 學習階段的改進

在學習階段，學生既可以從教師學到知識，又可以通過學生之間的相互學習進行提升。在式（6）中，學習階段的學生只受兩名學生的影響，忽略了教師的影響。所以利用差分進化算法中的變異策略，對學習階段進行了更新：

X^new2_i，M1=

X⁰_i，M1+rand（X_i，MBest－X⁰_i，M1）

f（X⁰_i，M1）gt;f（X_i，M2）

X⁰_i，M1+rand（X_i，MBest－X⁰_i，M1）+rand（X_i，M2－X⁰_i，M1） f（X⁰_i，M1）lt;f（X_i，M2） （10）

其中：X_i，M1和X_i，M2表示在第i次迭代過程中兩名互異的學生。若X⁰_i，M1優于X_i，M2，則X⁰_i，M1向X_i，MBest學習；若X_i，M2優于X⁰_i，M1，則X⁰_i，M1既向X_i，MBest學習又向X_i，M2學習。

利用差分變異策略對教學階段和學習階段進行更新，使算法的全局搜索能力和自適應性增強，根據學生的不同學習水平和需求，通過差分的方式制定個性化的教學計劃和教學策略，以提高教學效果。

4 融合差分教學優化的粗糙集屬性約簡算法

首先將屬性進行離散化處理，采用二進制編碼方式，再結合適應度函數給出融合差分教學優化的粗糙集屬性約簡算法。

4.1 算法描述

1）編碼方式和求核屬性

對連續型數據進行屬性約簡時需要首先對原始數據進行離散化，本文用二進制進行編碼，利用屬性依賴度的方式來求核。在初始化種群時，核屬性位置設為1，其余屬性則通過比較屬性依賴度與隨機數來設定，依賴度大于隨機數則初始化為1，否則為0。

2）適應度函數

f（p）=μ₁×γ_pγ_C+μ₂×card（C）－card（p）card（C）（11）

其中：card（C）表示種群對應二進制字符串長度；card（p）表示二進制串中“1”的個數。適應度函數引導種群進行約簡，μ₁值越大，約簡效果越顯著，越貼近粗糙集的約簡標準，μ₂越大表示刪減掉的屬性數目越多。因此在本文中取μ₁=0.7，μ₂=0.2。

4.2 AR-DTLBO算法流程

本文結合了差分教學優化算法的全局搜索能力和粗糙集理論在處理不精確和不確定數據方面的優勢，提出融合差分教學優化的粗糙集屬性約簡算法（AR-DTLBO），算法具體步驟如下：

算法1 AR-DTLBO算法

輸入：決策表S=〈U，R，V，f〉。

輸出：最小相對約簡。

a）計算各個屬性的依賴度，求出核屬性core（C），若γ_core（C）=γ_C，則core（C）為最小相對種群約簡，終止運行，否則執行步驟b）。

b）初始化種群。

（a）在種群初始化階段，設定核屬性位置為1，對于其他屬性位置，通過比較其屬性依賴度與隨機生成的數值來決定其初始化值：若依賴度高于隨機數，則位置設為1，否則設為0。

（b）根據式（11）計算各種群的適應度值，由式（3）計算初始水平，設置學習科目D，學生數目N，設置最大迭代次數為200次。

c）教學階段：首先根據式（7）對教學因子進行改進，其次根據式（8）和（9）對學生學習水平進行更新，若f（X¹_{i， j，M}）gt;f（X⁰_{i， j，M}），則更新f（X⁰_{i， j，M}），否則不進行更新。

d）學習階段：根據式（10）更新，得到X^new2_i，M1。

e）若全局最優學習水平連續10次保持不變，或算法達到設定的最大迭代次數，則算法終止執行。最優學習水平為最小相對約簡，否則轉步驟b）繼續執行。

4.3 AR-DTLBO算法偽代碼

算法2 AR-DTLBO算法

輸入：決策表。

輸出：最優學習水平。

4.4 算法復雜度分析

AR-DTLBO算法的時間復雜度主要取決于學生總數NP、變量維度D、數據集屬性數量M、樣本數量N。差分變異是算法的核心，在每一次迭代中，算法需要對個體執行變異操作，其時間復雜度為O（NP×D）。教學優化算法在每一代中包括教學和學習兩個主要的階段。在教學階段，算法計算整個種群的平均解，時間復雜度為O（NP×D），學習階段是通過學生之間的相互學習得到解，時間復雜度為O（NP×D）。因此，TLBO算法的總時間復雜度為O（2×NP×D）。粗糙集屬性約簡的時間復雜度為O（2^M×N），但通過TLBO算法可以大大減少搜索空間，從而降低時間復雜度，即AR-DTLBO算法的總體時間復雜度為O（2×NP×D+2^M×N）。

例1 下列信息系統是發表在Popular Science上的CTR（car test results）數據庫，如表1所示。

其中屬性是：

x₁—size，overall length，x₂—number of cylinders，x₃—presence of a turbocharer，x₄—type of fuel system，x₅—engine displacement，x₆—compression ratio，x₇—power，x₈—type of transmission，x₉—weight， y—mileage

屬性值如下：

c—compact，s—subcompact，sm—small，y—yes，n—no，E—EFI，B—2_BBL，m—medium，ma—manual，h—high，he—heavy，l—light，lo—low，a—auto.

根據AR-DTLBO算法約簡過程如下：

a）計算各個屬性的依賴度，得到核屬性為R={x₄，x₇，x₉}；

b）進行初始化，根據式（11）計算各種群的適應度值；

c）根據改進后的教學優化算法進行更新，最優學習水平為最小相對約簡，約簡長度為2，得到約簡結果為R={x₄，x₉}。

根據AR-DTLBO算法得到的約簡，比粗糙集模型的算法所得結果更優，驗證了AR-DTLBO算法的可行性。

5 實驗結果及分析

5.1 實驗設置

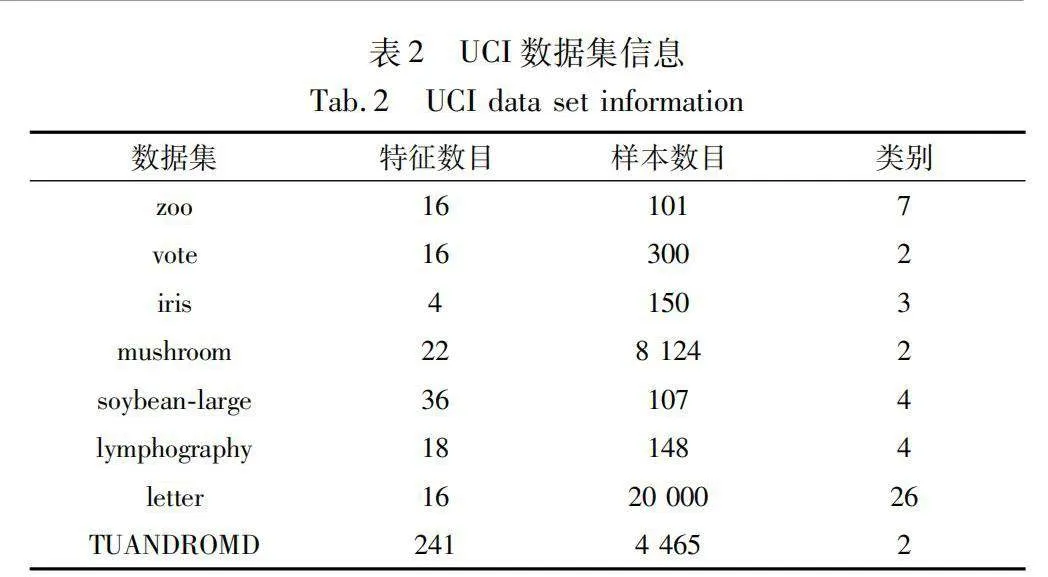
本文選取8組國際通用的UCI數據集進行仿真實驗，并進行對比分析。選取的數據集如表2所示，為減少各屬性量綱不一致對結果的影響，實驗中將所有屬性值歸一化處理。仿真實驗算法性能測試實驗在PC機上進行，實驗的硬件、軟件環境為：IntelCore^TMi7-6300HQ CPU @ 2.30 GHz處理器，12 GB 內存，操作系統為Windows 11（64位）；實驗算法使用Python語言進行編程實現，迭代次數設置為200次。

為了驗證AR-DTLBO算法的有效性，在表2中8個UCI測試數據集上通過與基于蟻群的屬性約簡算法（ACORS）^［6］、基于粒子群的屬性約簡算法（PSORS）^［7］、基于人工魚群的鄰域粗糙集屬性約簡算法（FSANRSR）^［8］、遺傳算法的屬性約簡算法（GARS）^［12］、基于遺傳粒子群的屬性約簡算法（GAPSO-RS）^［19］、基于改進魚群的鄰域粗糙集屬性約簡算法（IFSANRSR）^［20］進行對比。算法參數設置如表3所示，迭代次數都設置為200次，對比實驗分為四組：

第一組實驗：對比不同算法的執行時間和約簡結果的長度。

第二組實驗：探究不同算法在處理不同樣本規模時的性能表現，及樣本規模與算法消耗時間之間的關系。

第三組實驗：根據約簡公式對比不同算法的屬性約簡率；

第四組實驗：采用十折交叉驗證法，對比不同算法獲得的約簡在支持向量機（SVM）、K-最鄰近（KNN，其中K=3）分類器中的平均分類精度^{［21， 22］}。

5.2 實驗結果與分析

在實驗結果中，時間單位采用毫秒，約簡率保留兩位小數，平均分類精度保留一位小數。對于優于其他算法的結果，用加粗形式進行標注。

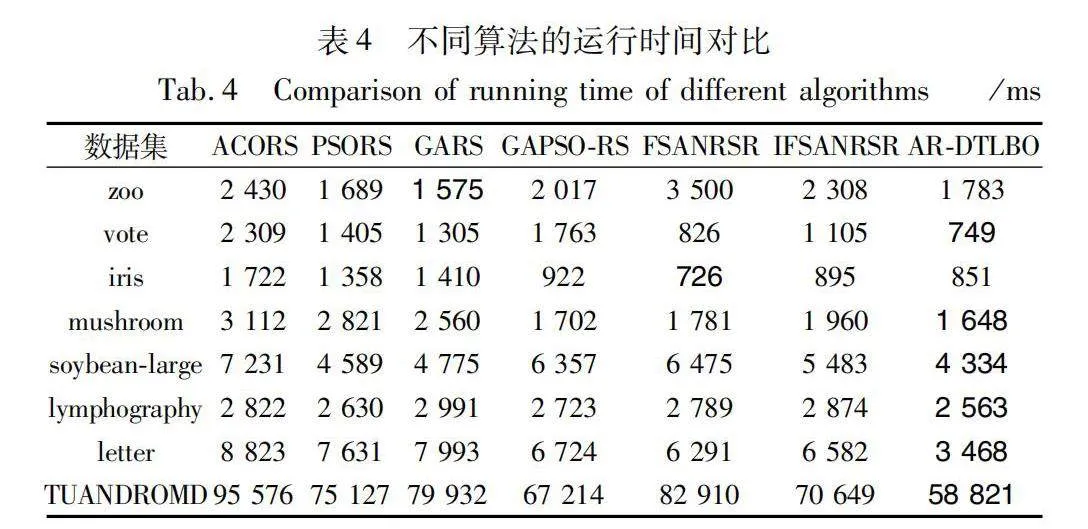
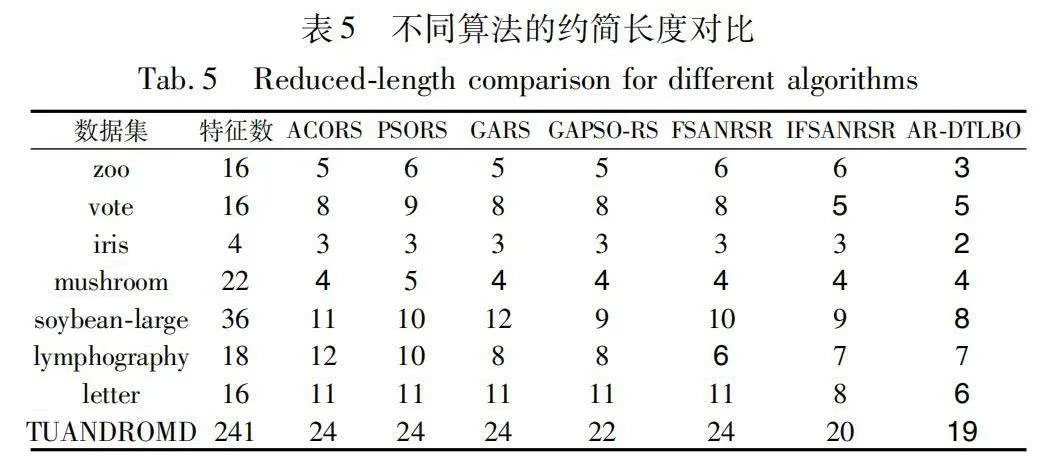
5.2.1 運行時間和約簡長度對比

表4、5展示了七種算法在8組數據集上的運行時間及約簡長度的對比結果。由表4可知，除了在數據集iris上，AR-DTLBO算法僅次于FSANRS算法，在其他數據集中，該算法的運行時間均低于其他六種對比算法。特別是在數據維度最大的數據集TUANDROMD上，ACORS、PSORS、GARS、GAPSO-RS、FSANRSR和IFSANRSR算法的運行時間分別是AR-DTLBO算法的1.62倍、1.28倍、1.36倍、1.14倍、1.41倍和1.20倍。在數據規模最大的數據集letter上，ACORS、PSORS、GARS、GAPSO-RS、FSANRSR和IFSANRSR算法的運行時間分別為AR-DTLBO算法的2.54倍、2.20倍、2.30倍、1.94倍、1.82倍和1.90倍。在數據規模遞增的zoo、soybean-large、lymphography和iris數據集中，AR-DTLBO算法在最小規模的數據集zoo上的運行效率稍遜于GARS算法。但當數據規模增大時，AR-DTLBO算法運行效率較GARS算法具有顯著優勢。

經過計算和分析，AR-DTLBO算法在8組數據集上的運行效率整體優于其他六種算法，尤其在處理大規模和高維數據時表現更佳。

由表5可知，AR-DTLBO算法在數據集zoo、iris、soybean-large、letter和TUANDROMD中的約簡長度相比其他六種算法要短，在vote和mushroom數據集中，七種算法的屬性約簡長度相同；在lymphography數據集中，AR-DTLBO算法的約簡長度僅次于FSANRSR算法。這證明了本文算法的有效性和可行性，能夠剔除冗余屬性，且在絕大多數數據集上都表現出了優越性。

5.2.2 迭代次數和運行時間對比

圖1展示了不同算法運行時間隨迭代次數增加的變化趨勢。各子圖中，橫軸代表迭代次數，縱軸為算法運行時間，每個數據集的迭代次數被均分為10個部分。

根據圖1可知，迭代次數增加時，算法的運行時間逐漸上升。在圖（b）（d）（g）（h）中可觀察到，隨著迭代次數的逐漸增加，AR-DTLBO算法運行時間始終低于其他六種算法。在圖（a）（c）中，GARS、FSANRSR算法的運行時間最短；在圖（e）（f）中迭代次數分別為80次、40次時，FSANRSR和AR-DTLBO算法的運行時間一樣；但當迭代次數逐漸增大時，AR-DTLBO算法的運行時間高于FSANRSR算法。由此更進一步驗證AR-DTLBO算法在大規模、高維數據上具有一定的優勢。

5.2.3 約簡率對比

對七種算法的約簡效果進行分析，采用約簡率來表示約簡結果。約簡率公式^［7］為

rate=|C|－|R||C|×100%（12）

其中：|C|表示數據集的條件屬性數；|R|表示約簡后的屬性個數。

根據表6可得，數據集iris的約簡率總體偏低，而在數據集vote、mushroom中，AR-DTLBO算法的約簡率與IFSANRSR算法相持平，在數據集lymphography中，AR-DTLBO算法的約簡率略遜于FANRSR算法。整體來說，AR-DTLBO算法相比其他算法的約簡率略高，并且能夠得到更好的約簡效果，因此AR-DTLBO算法具有良好的全局尋優能力。

5.2.4 分類精度對比

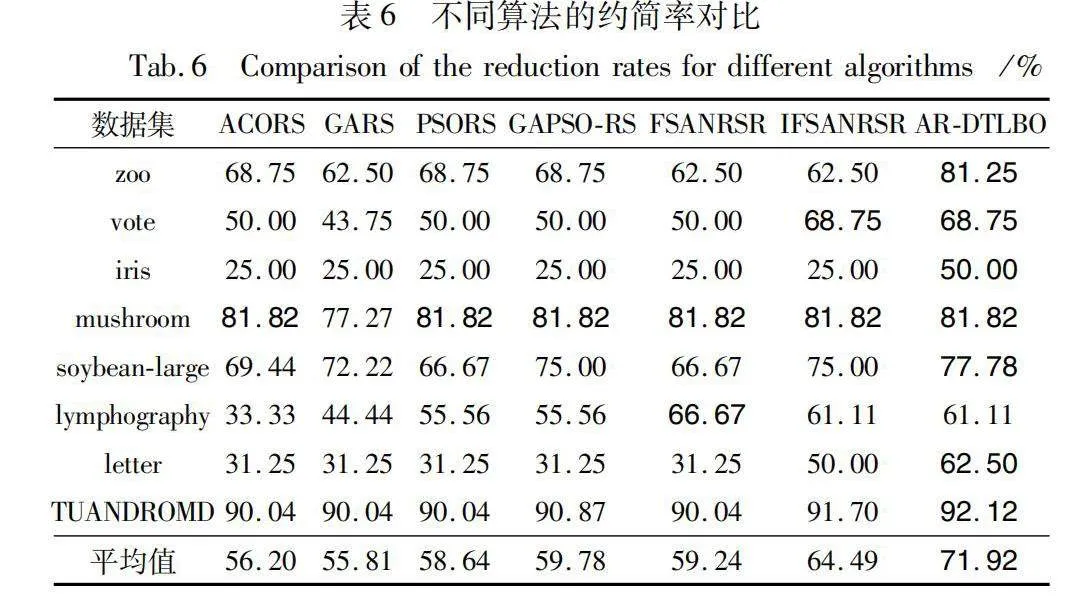
七種算法的約簡結果通過KNN（K=3）和SVM兩種分類模型進行了對比，對比結果詳見表7和8。

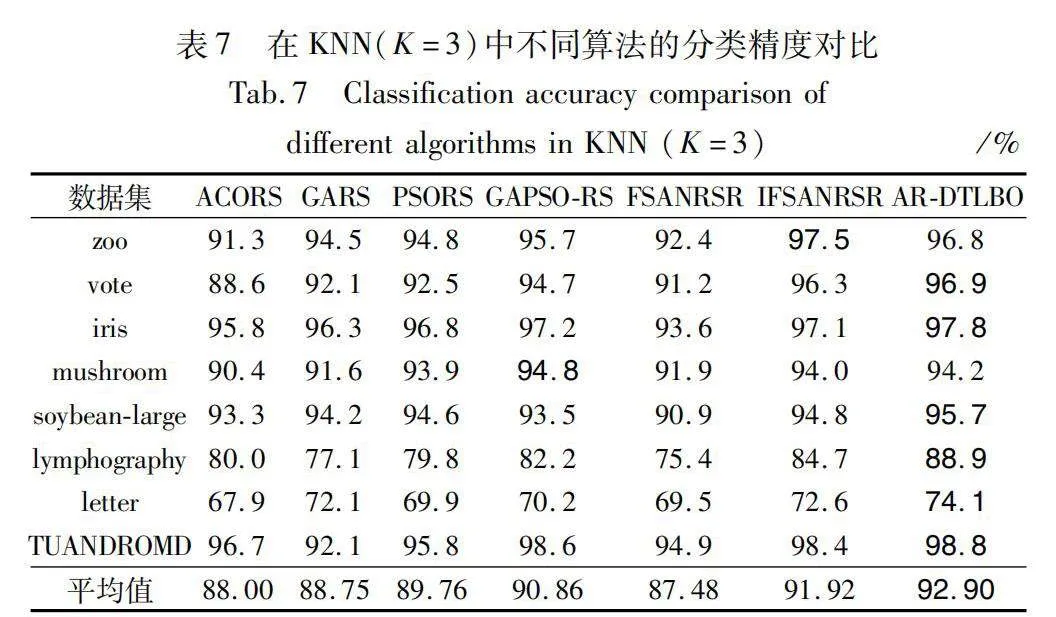
七種算法的平均分類精度差異較小，不同分類器的分類精度不同。由KNN和SVM兩種分類器可知，AR-DTLBO算法在屬性約簡結果是準確的，且具有較好的分類性能。

根據表7所示，在zoo數據集上，AR-DTLBO算法在KNN分類中的精度略遜于IFSANRSR算法；在mushroom數據集上，其精度略遜于GAPSO-RS算法。但在其他數據集上，其分類精度均高于其他六種算法。總體而言，AR-DTLBO算法的平均分類精度相比其他六種算法有顯著提升。

根據表8所示，在數據集zoo、lympho-graphy上，AR-DTLBO算法略遜于PSORS、IFSANRSR算法的精度，在數據集iris上，AR-DTLBO與IFSANRSR算法相持平。在其他數據集上，AR-DTLBO算法的分類精度均高于其他六種算法，AR-DTLBO算法的平均分類精度比其他六種算法分別提高了1.05%、1.02%、1.02%、1.03%、0.98%和1.04%。

根據以上四組實驗結果及其分析可知，AR-DTLBO算法不僅在計算效率上優于ACORS、PSORS、GARS、GAPSO-RS、FSANRSR、IFSANRSR算法，而且在約簡長度、約簡率、兩種分類器中的分類性能都具有顯著優勢。因此提出的融合差分教學優化的粗糙集屬性約簡算法是可行、有效的。

6 結束語

針對屬性約簡提出一種新穎的方法，即融合差分教學優化算法的粗糙集屬性約簡算法。AR-DTLBO算法通過結合差分教學優化算法的全局搜索能力和粗糙集在處理不確定數據方面的優勢，實現了對原始數據集的有效約簡和優化，提高了屬性約簡的效率和準確性。通過在UCI上的實驗表明，AR-DTLBO算法在多個數據集上均取得了顯著的約簡效果，且在處理高維數據集時有明顯的優勢，能夠有效減少屬性集的維度并保持數據信息的完整性。但仍存在參數調整困難、對初始解依賴性強的缺點。未來，考慮將AR-DTLBO算法應用于更廣泛的實際問題中。

參考文獻：

［1］Pawlak Z. Rough sets ［J］. International Journal of Information and Computer Sciences， 1982， 11（5）： 431-356.

［2］Muhammad S R， Usman Q. Feature selection using rough set-based direct dependency calculation by avoiding the positive region ［J］. International Journal of Approximate Reasoning， 2018， 92： 175-197.

［3］Wang Changzhou， Huang Yang， Shao Mingwen， et al. Fuzzy rough set-based attribute reduction using distance measures ［J］. Knowle-dge Based Systems， 2019，164： 205-212.

［4］張敏， 朱啟兵. 基于加權鄰域依賴度的非單調性屬性約簡 ［J］. 計算機仿真， 2023， 40（3）： 395-399. （Zhang Min， Zhu Qibing. Non-monotonicity property reduction based on weighted neighborhood dependence ［J］. Computer Simulation， 2023， 40（3）： 395-399.）

［5］景運革， 景羅希， 王寶麗，等. 屬性值和屬性變化的增量屬性約簡算法 ［J］. 山東大學學報： 理學版， 2020， 55（1）： 62-68. （Jing Yunge， Jing Luoxi， Wang Baoli， et al. Incremental attribute reduction algorithm for attribute value and attribute change ［J］. Journal of Shandong University： Science Edition， 2020， 55（1）： 62-68.）

［6］吳尚智， 張文超， 佘志用，等. 利用蟻群優化算法的粗糙集屬性約簡方法 ［J］. 計算機工程與科學， 2019， 41（3）： 538-544. （Wu Shangzhi， Zhang Wenchao， She Zhiyong， et al. Rough set attribute reduction method using ant colony optimization algorithm ［J］. Computer Engineering and Science， 2019， 41（3）： 538-544.）

［7］欒雨雨， 王錫淮， 肖健梅. 基于粒子群的粗糙集屬性約簡算法 ［J］. 計算機仿真， 2021， 38（7）： 271-275. （Luan Yuyu， Wang Xihuai， Xiao Jianmei. Rough set attribute reduction algorithm based on chaotic discrete particle swarm ［J］. Computer Simulation， 2021， 38（7）： 271-275.）

［8］Chen Yumin， Zeng Zhiqiang， Lu Junwen. Neighborhood rough set reduction with fish swarm algorithm ［J］. Soft Compute， 2017， 21（23）： 6907-6918.

［9］白建川， 夏克文， 牛文佳，等. 新型灰狼算法的粗糙集屬性約簡及應用 ［J］. 計算機工程與應用， 2017， 53（24）： 182-186. （Bai Jianchuan， Xia Kewen， Niu Wenjia， et al. Rough set property reduction and application of the new gray wolf algorithm ［J］. Computer Engineering and Applications， 2017， 53（24）： 182-186.）

［10］Mohamed S R， Hassaning A E. An improved social spider optimization algorithm based on rough sets for solving minimum number attri-bute reduction problem ［J］. Neural Computing and Applications，2018，30（8）：2441-2452.

［11］Rao R V， Savsani V J. Teaching learning based optimization： a novel method for constrained mechanical design optimization problems ［J］. Computer-Aided Design， 2011，43： 303-315.

［12］Cheng Yong， Zheng Zhongen， Wang Jun. Attribute reduction based on genetic algorithm for the coevolution of meteorological data in the industrial Internet of Things ［J］. Wireless Communications amp; Mobile Computing， 2018， 27（13）： 1530-1546.

［13］Chen Zhixiang. Group-individual multi-mode cooperative teaching-learning-based optimization algorithm and an industrial engineering application ［J］. Journal of Intelligent amp; Fuzzy Systems， 2023， 44（3）： 5437-5465.

［14］Lu Shichang， Liu Danyang， Li Dan， et al. Enhanced teaching-learning-based optimization algorithm for the mobile robot path planning problem ［J］. Applied Science， 2023， 13（4）： 2291-2314.

［15］Moazeni A， Khorsang R， Ramezanpour M. Dynamic resourceallocation using an adaptive multi-objective teaching-learning based optimization algorithm in cloud ［J］. IEEE Access， 2023 （11）： 23407-23419.

［16］Tang Hongtao， Fang Bo， Liu Rong， et al. A hybrid teaching and learning-based optimization algorithm for distributed sand casting job-shop scheduling problem ［J］. Applied Soft Computing， 2022 （120）： 108694-108715.

［17］Liang Shaohui， Wei Botao. Improved teaching-learning based optimization algorithm based on fusion difference mutation ［J］. Journal of Intelligent amp; Fuzzy Systems， 2023， 1（1）： 4643-4651.

［18］Wang Minghao， Ma Yongjie. A differential evolution algorithm based on accompanying population and piecewise evolution strategy ［J］. Applied Soft Computing， 2023， 8（143）： 1568-4946.

［19］吳尚智， 羅藝純， 翟敬鵬. 基于遺傳粒子群和粗糙集的最小屬性約簡算法 ［J］. 計算機工程與科學， 2016， 38（5）： 1007-1013. （Wu Shangzhi， Luo Yichun， Zhai Jingpeng. Minimum property reduction algorithm based on genetic particle swarm and rough set ［J］. Computer Engineering and Science， 2016， 38（5）： 1007-1013.）

［20］Li Zou， Li Hongxin， Wei Jiang. An improved fish swarm algorithm for neighborhood rough set reduction and its application ［J］. IEEE Access， 2020， 7（5）： 90277-90288.

［21］王小雪， 殷鋒， 楊雅雯. 基于知識粗糙熵的快速屬性約簡算法 ［J］. 計算機應用研究， 2024， 41（2）： 488-492. （Wang Xiaoxue， Yin Feng， Yang Yawen. Fast attribute reduction algorithm based on knowledge rough entropy ［J］. Application Research of Compu-ters， 2024， 41（2）： 488-492.）

［22］唐鵬飛， 張賢勇， 莫智文. 基于依賴度的區間集決策信息表屬性約簡 ［J］. 計算機應用研究， 2021， 38（11）： 3300-3303， 3309. （Tang Pengfei， Zhang Xianyong， Mo Zhiwen. Attribute reduction based on dependency degree for interval-set decision information tables ［J］. Application Research of Computers， 2021， 38（11）： 3300-3303， 3309.