改進的分布估計鯨魚算法求解區塊鏈DAG任務調度問題

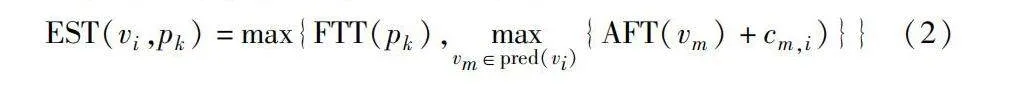
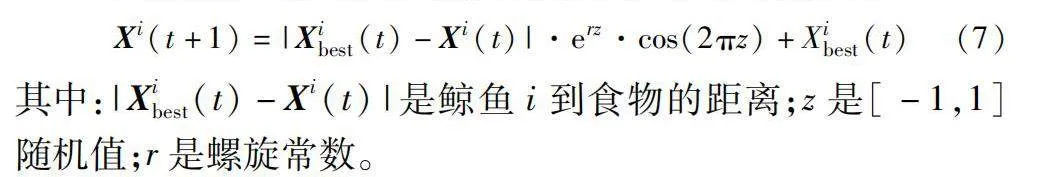
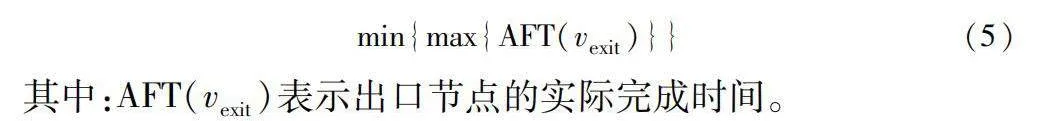
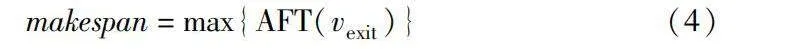
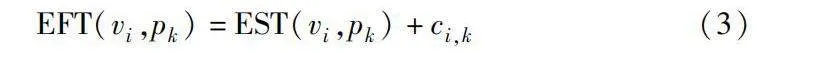
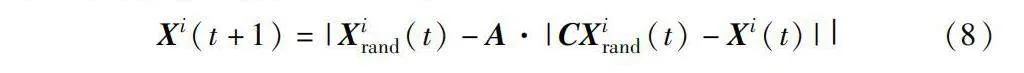
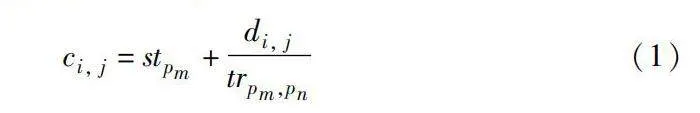
摘 要：為了克服區塊鏈單鏈技術效率低的問題，一種新的范式有向無環圖正在蓬勃發展。針對區塊鏈有向無環圖中考慮代價權重的非獨立任務調度問題，構建了區塊鏈DAG的任務調度數學模型，并為了求解該問題提出了一種基于改進分布估計鯨魚的新任務調度算法。新算法在WOA中引入EDA的空間采樣和統計學習來預測搜索的最佳區域，進而產生優秀的新個體，從而使得新算法具備更強的全局搜索能力和更快的收斂速度。最后通過程序仿真，對比了多種算法在收斂速度和全局尋優能力方面的性能。實驗表明IEWOA比傳統的WOA和EDA在以上參數性能有明顯優勢，相比于改進遺傳算法FPGA，IEWOA同樣在參數性能上有一定的優勢。

關鍵詞：DAG；分布估計；鯨魚算法；任務調度

中圖分類號：TP18 文獻標志碼：A 文章編號：1001-3695（2024）11-023-3364-06

doi：10.19734/j.issn.1001-3695.2024.04.0094

Improved distribution estimation whale algorithm for block chain DAG task scheduling

Xu Jun¹， Peng Junfeng^{1， 2}， Tang Yong²， Wang Jihong¹， Cai Weishan¹

（1.School of Computing， Guangdong University of Education， Guangzhou 510303， China; 2.School of Computing， South China Normal University， Guangzhou 510631， China）

Abstract：In order to overcome the efficiency issues of single chain technology in blockchain， a new paradigm directed acyclic graphs is flourishing. This article focused on the non independent task scheduling problem considering cost weights in blockchain directed acyclic graphs， and constructed a mathematical model for task scheduling in blockchain DAG， and proposed a new task scheduling algorithm based on improved distribution estimation whale to solve this problem. The new algorithm introduced spatial sampling and statistical learning of EDA in the WOA algorithm to predict the optimal search area， thereby gene-rating excellent new individuals， making the new algorithm have stronger global search ability and faster convergence speed. Finally， through program simulation， it compared the performance of multiple algorithms in terms of convergence speed and glo-bal optimization ability. The experiments show that IEWOA has significant advantages over traditional WOA and EDA in the above parameter performance. In addition， comparing with the improved genetic algorithm FPGA， IEWOA also has certain advantages in parameter performance.

Key words：DAG; distribution estimation; whale algorithm; task scheduling

0 引言

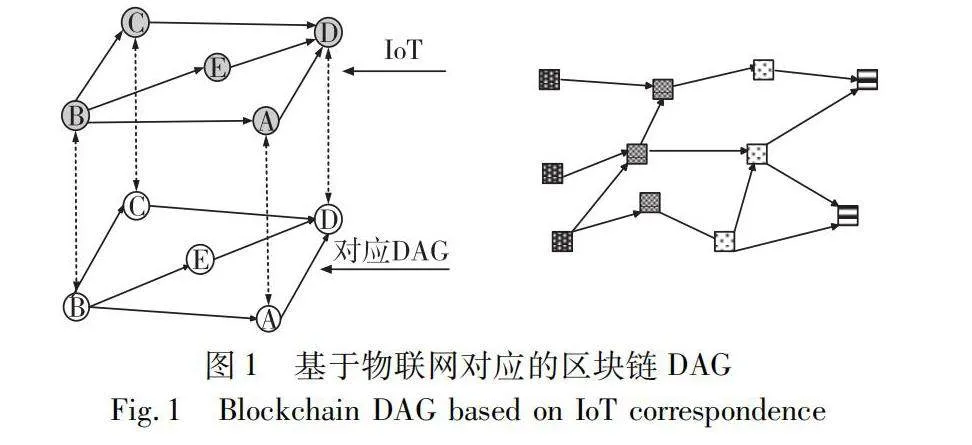
區塊鏈是當今討論最多的技術之一^［1，2］，是由公共或私有網絡組成的交易數字賬本，每隔一段時間的一組交易被連續打包在區塊中。區塊鏈以前被設計為一種加密貨幣^［3，4］，并被認為是分類賬或分布式數據庫的一種創新方法，其中非理性數據也可以保存在交易的元數據中。區塊鏈數據庫或分類賬包含交易和區塊兩個級別的記錄。區塊中包含一個或多個事務的列表，每個塊帶有時間戳并鏈接到上一個塊。為確保區塊鏈數據的安全，塊中的數據以加密形式存儲。由于每個塊包含前一個塊的哈希，所以每個塊將與前一個塊鏈接，形成類似鏈表的數據結構。然而第一個塊卻沒有先前鏈接的塊，因此其先前的哈希值設置為NULL，稱為創世塊。這種單鏈區塊鏈技術在可擴展性、成本和效率方面存在一定的局限性，這阻礙了其在需要高效微交易的應用中的發展，如單鏈技術無法支持高并發的需求、鏈與鏈之間不能互通互聯、無法適應不同的應用場景等，這些缺點對其在新興物聯網（IoT）應用中的適應性有重大影響^［5～10］。有向無環圖（DAG）如圖1所示，因其在物聯網中的特殊含義而徹底改變了區塊鏈技術^{［11～14］}，由于其優化驗證、高可擴展性、高效來源、物聯網支持和多方參與等特點，導致這種區塊鏈DAG技術正在迅速發展^{［15～17］}，而其中DAG（有向無環圖）任務調度問題也成為研究熱點之一。

DAG任務調度一般目標是最小化任務執行時間 （make-span），該問題是一個完全NP問題^［18］，因此大多數研究都是基于啟發式算法。例如文獻［19］提出了一種使用強化學習的蒙特卡羅樹搜索（MCTS）信任感知自適應DAG任務調度算法，該方法使用強化學習模型進行定義，確定在可信和不可信實體中同時執行DAG任務時的實際調度策略。文獻［20］提出一種最短剩余時間優先 （distributed shortest remaining time first， D-SRTF），在搶占式調度中，能夠優先執行剩余執行時間最短的任務，適用于動態變化的任務執行時間，需要頻繁地進行任務切換，可能增加調度開銷，不適用于任務切換開銷較大的情況。文獻［21］提出了最早截止時間優先 （earliest deadline first，EDF），可能導致長任務長期等待，影響任務的響應時間，不適用于短任務密集型的場景。以上這些任務調度算法都不考慮異構復雜環境下的通信開銷， 而區塊鏈DAG任務調度卻是在復雜異構網絡環境下進行的， 因此以上算法不適用。為解決復雜異構網絡環境下區塊鏈DAG任務調度問題，文獻［22］提出了一種改進FPGA遺傳算法，具有較好的全局搜索能力，適用于復雜的任務調度問題，但也需要較長的計算時間和資源。同樣針對復雜異構網絡環境下區塊鏈DAG任務調度問題，本文提出了改進分布估計鯨魚任務調度算法（IEWOA）。該算法是一種用于優化區塊鏈DAG網絡中任務調度的算法，其目標是通過合理分配任務和資源，充分滿足區塊鏈DAG任務調度問題。通過對比了文獻［22］的FPGA、WOA和EDA，IEWOA在參數性能上有一定的優勢。

1 區塊鏈DAG的任務調度問題建模

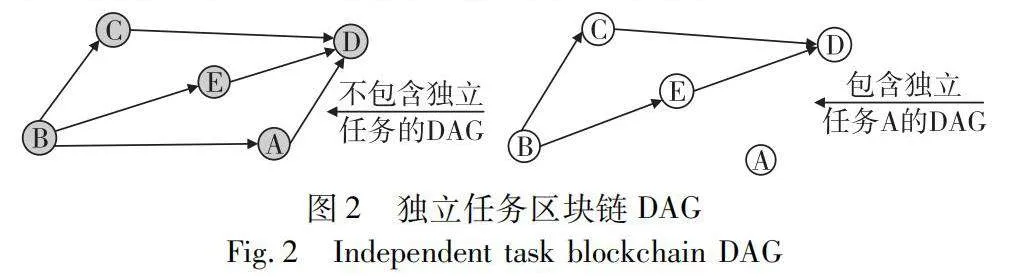
區塊鏈DAG任務調度是在區塊鏈網絡中，根據任務之間的依賴關系和執行時間，合理地安排任務的執行順序，以最小化整體任務的執行時間。在區塊鏈中，任務可以是智能合約的執行、交易的確認和數據的處理等。另外這些任務可以是獨立的，也可以是非獨立的。獨立任務是指彼此之間沒有依賴關系，可以獨立執行的任務。非獨立任務則是指彼此之間存在依賴關系，需要按照一定的順序或條件進行執行的任務。獨立任務可以同時進行，而非獨立任務需要滿足其依賴關系才能執行。例如，一個任務可能需要等待前一個任務的結果才能開始執行，或者多個任務之間存在數據共享或交互的依賴關系。因此，區塊鏈的DAG中既包含獨立任務，也包含非獨立任務如圖2所示，本文研究的任務調度算法需要考慮任務之間的依賴關系和執行順序，以實現有效的任務調度和優化。

1.1 數學符號定義

在圖2中，節點的權值表示任務的執行時間，有向邊表示任務間的依賴關系即后繼任務必須在它的前驅任務處理完畢后才能開始執行，邊的權值表示任務間的通信開銷。為了準確描述DAG的區塊鏈任務調度問題的數學模型，假定區塊鏈的DAG拓撲為G，給出下列符號定義：

V為有向無環圖G所有任務的集合，n為任務數；

P為有向無環圖G所有處理器節點的集合，m為任務數；

E為有向無環圖G所有任務之間依賴關系的邊集合；

D={d_{i， j}|v_i，v_j∈V}為n×n二維矩陣，d_{i， j}表示v_i任務與依賴的v_j之間數據通信開銷；

VP={vp_{i， j}|v_i∈N，p_j∈M}為n×m二維矩陣，vp_{i， j}表示v_i任務在處理節點p_i的執行時間；

ST是處理節點啟動通信的一維時間矩陣，st_pi是處理節點p_i的通信啟動時間；

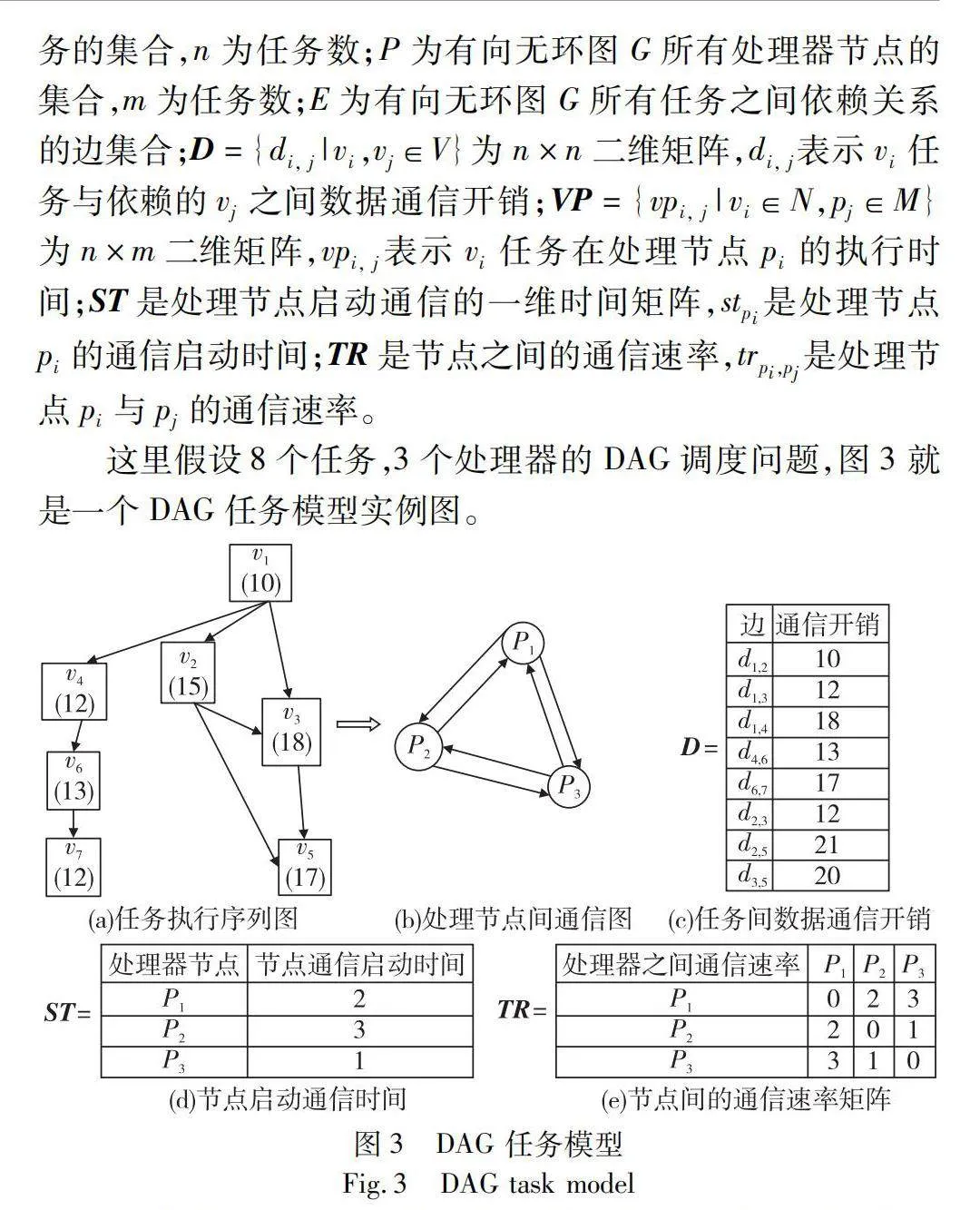
TR是節點之間的通信速率，tr_pi，pj是處理節點p_i與p_j的通信速率。

這里假設8個任務，3個處理器的DAG調度問題，圖3就是一個DAG任務模型實例圖。

假設任務v_i是v_j的前繼任務，并且被分別分配到節點p_k和p_q上執行時，通信代價數學計算公式為

c_{i， j}=st_pm+d_{i， j}tr_pm，pn（1）

如果p_m=p_n就是這兩個任務剛好分配到同一個處理節點，那么這里就把通信成本設置為0。

1.2 區塊鏈DAG任務調度目標函數

DAG的makespan是指在一個有向無環圖中完成所有任務所需的最長時間。在一個DAG中，每個任務都有一個預計的執行時間。每個任務的執行時間可能不同，且任務之間存在依賴關系。例如，任務B可能依賴于任務A的完成，只有在任務A完成后才能開始執行任務B。DAG的makespan是指在滿足所有任務依賴關系的前提下，完成所有任務所需要的最長時間。假設每個任務的執行時間已知，并且所有任務的依賴關系已經確定，可以使用拓撲排序算法來計算DAG的makespan。通過拓撲排序算法，可以有效地計算DAG的makespan，并找到最優的任務執行順序，以最小化完成所有任務所需的時間。

為了準確地描述目標函數的意義，下面給出異構網絡環境下DAG 任務調度問題中常見的定義及公式。

定義1 最早開始時間（earliest start time，EST）。

任務v_i在p_k上的最早開始時間為

EST（v_i，p_k）=max{FTT（p_k），maxv_m∈pred（v_i）{AFT（v_m）+c_m，i）}}（2）

其中：FTT（p_k）代表p_k完成最后一個任務的時間；AFT（v_m）代表v_m完成最后一個任務的時間。

定義2 最早完成時間（earliest finish time，EFT）。

EFT（v_i，p_k）=EST（v_i，p_k）+c_i，k（3）

定義3 調度長度（makespan）。

makespan=max{AFT（v_exit）}（4）

有序DAG是一個有向無環圖，為NP問題^［18］。本文目標為最小化并行應用程序的最早完成時間［makespan］，參照文獻［1］，目標函數的公式為

min{max{AFT（v_exit）}}（5）

其中：AFT（v_exit）表示出口節點的實際完成時間。

跨度是一個主要、常見的目標，指的是調度的長度，也就是從第一個任務開始運行到最后一個任務運行完畢所經歷的時間。跨度越小說明調度策略越好。當用戶向網格系統提交任務后，最大的愿望是網格系統盡快完成自己的任務。

以上構建的區塊鏈DAG任務調度數學模型正是考慮異構復雜環境下的通信開銷， 為解決復雜異構網絡環境下區塊鏈DAG任務調度問題，文獻［22］提出了一種改進FPGA遺傳算法，具有較好的全局搜索能力，適用于復雜的任務調度問題，但也需要較長的計算時間和資源。而本文同樣針對復雜異構網絡環境下的區塊鏈DAG任務調度問題，提出了一種改進分布估計鯨魚任務調度算法。該算法融合分布估計的搜索空間采樣和統計學習來預測搜索的最佳區域， 進而產生優秀的新個體，從而提升算法的全局搜索能力和收斂性。另外本文之所以選用鯨魚算法進行改進優化，是因為WOA的三個種群更新機制相互獨立，使得算法在尋優階段能夠分別運行及控制全局探索和局部開發過程。與其他群體智能優化算法相比，WOA不需要人為設置各種控制參數值，簡化了算法的使用并降低了應用難度，在多種測試中WOA展現出了優于蟻群算法和粒子群算法等其他智能優化算法的尋優性能^{［23，24］}。

2 算法描述

2.1 鯨魚優化算法

鯨魚優化算法（whale optimization algorithm，WOA）是一種基于自然界鯨魚狩獵行為的元啟發式算法。該算法模擬了鯨魚的社會行為和狩獵策略，用于解決優化問題。鯨魚優化算法的基本思想是通過模擬鯨魚的追蹤行為和呼叫行為來搜索最優解。算法中的個體被稱為鯨魚，它們在搜索空間中移動并調整自身位置和速度。每個鯨魚根據自身的適應度值和全局最優解來更新自己的位置和速度，以尋找更優的解。鯨魚優化算法的主要步驟包括初始化種群、計算適應度值、更新位置和速度、調整搜索范圍等。通過多次迭代和交互，鯨魚優化算法逐漸收斂到最優解。鯨魚優化算法具有以下特點：

a）算法簡單易實現，不需要過多的參數設置；

b）可以應用于各種優化問題，包括連續優化和離散優化；

c）具有較好的全局搜索能力和收斂性能；

d）算法具有自適應性，能夠自動調整搜索范圍。

鯨魚優化算法已經在工程優化、機器學習、圖像處理等多個領域得到應用。它在解決復雜優化問題方面具有一定的優勢，并且在一些實際問題中取得了較好的效果。

鯨魚優化算法包括的這三個核心算子，如下所示。

a）包圍獵物。該行為數學模型等式表示為

Xⁱ（t+1）=|Xⁱ_best（t）－A·|CXⁱ_best（t）－Xⁱ（t）||（6）

其中：t表示當前迭代次數；A和C表示相關系數；Xⁱ（t）表示當前位置向量；Xⁱ_best（t）表示現有最優解。

b）氣泡網攻擊方式。該行為數學模型等式表示為

Xⁱ（t+1）=|Xⁱ_best（t）－Xⁱ（t）|·e^rz·cos（2πz）+Xⁱ_best（t）（7）

其中：|Xⁱ_best（t）－Xⁱ（t）|是鯨魚i到食物的距離；z是［-1，1］隨機值；r是螺旋常數。

c）尋找獵物。當Agt;1時，鯨魚根據自身位置隨機搜索獵物。該行為數學模型等式表示為

Xⁱ（t+1）=|Xⁱ_rand（t）－A·|CXⁱ_rand（t）－Xⁱ（t）||（8）

其中：Xⁱ_rand（t）是隨機鯨魚在種群中的位置；控制參數向量A=2rand·a－a和C=2rand，a隨著迭代次數的增加從2線性減小到0，rand是分布于［0，1］的隨機向量。

2.2 分布估計算法

分布估計算法 （EDA）^{［25～27］}是一種新興的基于統計學原理的隨機優化算法。EDA與遺傳算法（GA）、鯨魚算法等優化算法有著明顯的區別。GA 采用交叉和變異等操作產生新個體， EDA 則通過對搜索空間采樣和統計學習來預測搜索的最佳區域， 進而產生優秀的新個體。相比于GA 基于基因的微觀層面的進化方式， EDA采用基于搜索空間的宏觀層面的進化方法， 具備更強的全局搜索能力和更快的收斂速度。EDA是一類用于估計未知概率分布的方法，通過從已有數據中學習概率分布的參數或者通過擬合一個合適的概率分布函數來近似未知分布。常見的分布估計算法包括最大似然估計（maximum likelihood estimation，MLE）、貝葉斯估計（Bayesian estimation）、核密度估計（kernel density estimation，KDE）等。分布估算法的核心算子是概率模型的建立。在分布估計算法中，表示解空間分布的概率模型是一個概率向量p（x）=（p（x₁），p（x₂），…，p（x_n）），其中p（x_i）表示位置i上取某數值的概率。概率模型的計算公式如下：

p_j+1（x）=（1－a）p_j（x）+a1N∑Nj=1x^j_i（9）

其中：p_j（x）表示第j次種群解空間的概率向量；x¹_i，x²_i，…，x^N_i表示N個優質解；x^j_i表示位置i上的取值；a表示學習因子。

2.3 改進的分布估計鯨魚DAG任務調度分配優化算法

1）編碼

采用十進制整數編碼。每一位置代表一種可行的任務調度分配方案。每一位置有2×n個維數（n表示需要分配的任務數）。其中每一維是1～n的十進制數。前面n維代表任務的序列，后面n維代表分配給任務的相應處理器，如表1所示。任務V₁提供給P₂處理器，任務V₂提供給P₁處理器，由此類推。

2）算法主要參數

a）種群數（PopSize），一般取30～50。 其實對于大部分的問題20個種群規模已經足夠可以取得好的結果， 不過對于比較難的問題或者特定類別的問題， 種群數可以取到100 或 200。可以通過仿真的結果而定。

b）單個種群每一維取值（TaskNum），前半段由算法設定的任務數數決定，后半段由給定的處理節點數決定。

3） 算法流程

WOA的主要優點是簡單性和速度。然而，WOA缺乏堅實的數學基礎，容易收斂到局部最優解。為了克服這些問題，本文嘗試在WOA中通過對搜索空間采樣和統計學習來預測搜索的最佳區域， 進而產生優秀的新個體。相比于FPGA 基于基因和WOA基于個體的微觀層面的進化方式， EDA采用基于搜索空間的宏觀層面的進化方法， 具備更強的全局搜索能力和更快的收斂速度，進而快速找到最優解。以下是整個IEWOA算法的具體步驟：

a）初始化迭代計數器、種群規模、最大迭代次數等初始參數，并隨機產生初始種群。

b）通過式（5）計算每個鯨魚的最佳目標函數值。

c）進入算法的主循環。如果plt;0.5且|A|lt;1，則每頭鯨魚將根據式（6）更新當前位置，否則plt;0.5且|A|≥1根據式（8）更新鯨魚個體位置。如果p≥0.5，每只鯨魚都根據式（7）更新其位置。

d）根據式（9）建立種群的概率模型，并進行隨機采樣產生新的群體。

e）排序。對新的鯨魚種群計算評估，以找到全局最優的鯨魚個體及其位置，并更新最優解。

f）如果滿足算法的終止條件（最大迭代次數），則結束并輸出最優解；否則，轉到步驟b）并繼續算法迭代。

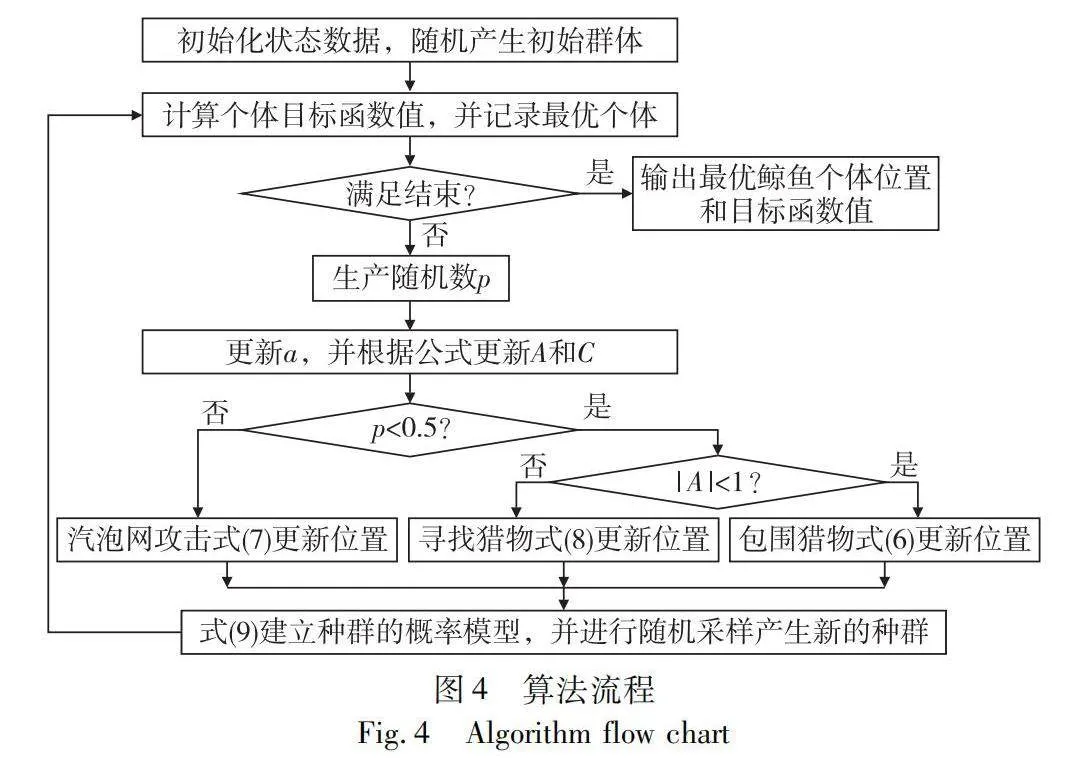
整個算法的流程如圖4所示。

3 模擬實驗與數據分析

模擬實驗平臺在由十臺機器組成的一組機器上進行測試。每臺機器的配置如下：操作系統為Cent OS 5.4系統；CPU為Intel Core i5-4590；內存為8 GB。實驗的區塊鏈DAG任務圖采用隨機產生，除了把 IEWOA 與傳統的 EDA 算法和WOA進行比較，還將IEWOA與文獻［24］的FPGA進行了比較，分別測試它們的收斂速度和尋優能力等方面性能。在隨機區塊鏈DAG任務圖中，任務處理節點個數從 10變化到 100，每次增加 10，每個任務的后繼任務個數取均值為 v/10的隨機數，任務在各處理機上的執行時間為［1，40］的任意數，任務間的數據傳輸量為［100，500］的隨機數；隨機生成處理機的通信啟動時間為［1，10］的整數，處理機間的傳輸率為［1，10］的任意數。

1）尋優性能

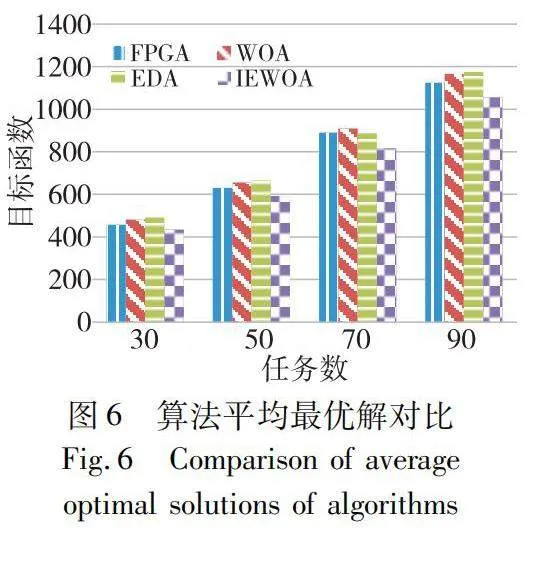
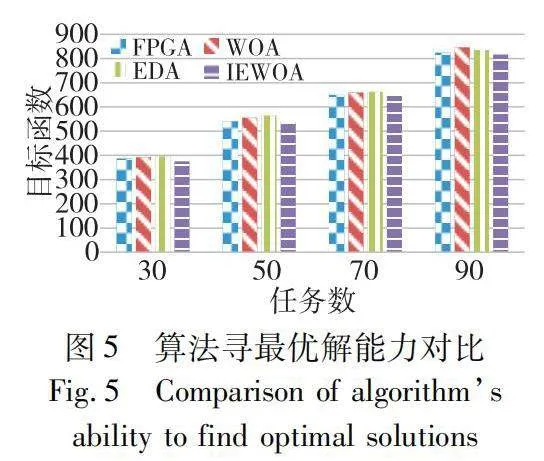
參數設置處理節點數為3，種群數為20，算法的迭代次數為100。尋優性能主要比較算法的尋最優解的能力和平均最優解的能力，圖5是不同任務數（30，50，70，90）情況下的算法尋最優解能力對比，圖6是各算法平均最優解（實驗重復20次取平均）的能力對比。

從圖5可以觀察到IEWOA對比其他三個算法，在任務數分別為30、50、70、90的分配要求下，每次都能獲取更優的目標函數值。雖然任務數為70和90 的情況下四種算法所獲得最優目標函數值相近，但任務數在30和50時IEWOA所獲得目標函數值優勢較為明顯。說明在任務分配和計算消耗資源較少的情況下，IEWOA具有更強的全局尋優的能力。

從圖6不難發現IEWOA尋找平均目標函數值的優勢更為明顯，而且更能體現算法的全局尋優能力和算法收斂性能。不僅對比傳統的WOA，還是相比于FPGA（基于基因）和WOA（基于個體）的微觀層面的進化方式， 融合EDA采用基于搜索空間的宏觀層面的IEWOA明顯具有更強全局搜索能力和更快的收斂速度。

2）改變種群規模

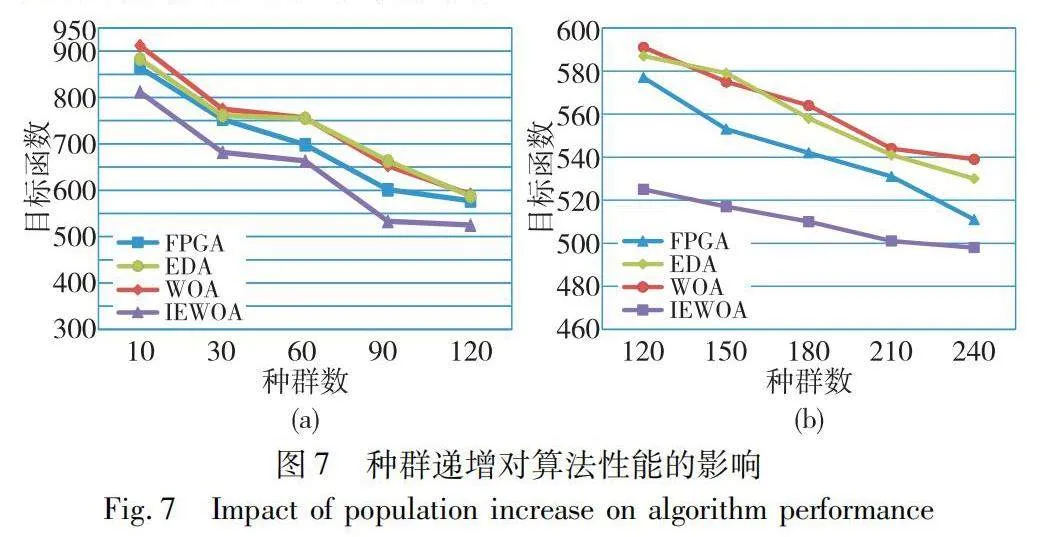
參數設置任務數為60，處理節點數為3，算法的迭代次數為300。圖7（a）是種群數分別為10、30、60、90、120的情況下，四種算法的尋優能力比較。很顯然隨著種群數的遞增，四個算法都能隨著種群數的增加而獲得更好的目標函數值。WOA、EDA和FPGA隨著種群數擴大所獲得的最優目標函數值趨近，而很明顯IEWOA較其他三種算法始終能獲得更優的目標函數值，而且隨著種群數的增加IEWOA優勢更加明顯。

為進一步驗證大種群規模對算法的影響及體現各算法的性能，參數設置同圖（a），而種群數分別為120、150、180、210、240的情況下，驗證四種算法的獲得的最優目標函數值的能力，實驗結果如圖7（b）所示。

從圖7（b）能發現當種群數從120遞增到240時，四種算法都隨著種群數的遞增所獲得最優目標函數值也逐漸變小。說明種群數的增加確實能增加算法全體多樣性從而影響算法的全局尋優能力，但同時可發現IEWOA始終都比其他三種算法所獲得最優解更好一點，而且隨種群數的增加這種優勢一直保持。隨著種群數的增加，其他三種算法也逐漸能尋找到更好的最優解，同時也發現改進FPGA比傳統EDA和WOA尋優能力要更強一些。最終這次實驗發現隨著種群數的增加四種算法都能不斷逼近全局最優解并且最終所獲得最終目標函數值都越來越接近，但IEWOA始終能比其他算法找到更優的解。這是由于IEWOA在傳統WOA中建立概率模型有利地保證了算法平穩地向最優解空間靠近，指導了算法的進化方向，使得IEWOA較其他算法具有更好的尋優能力。

3）改變迭代次數

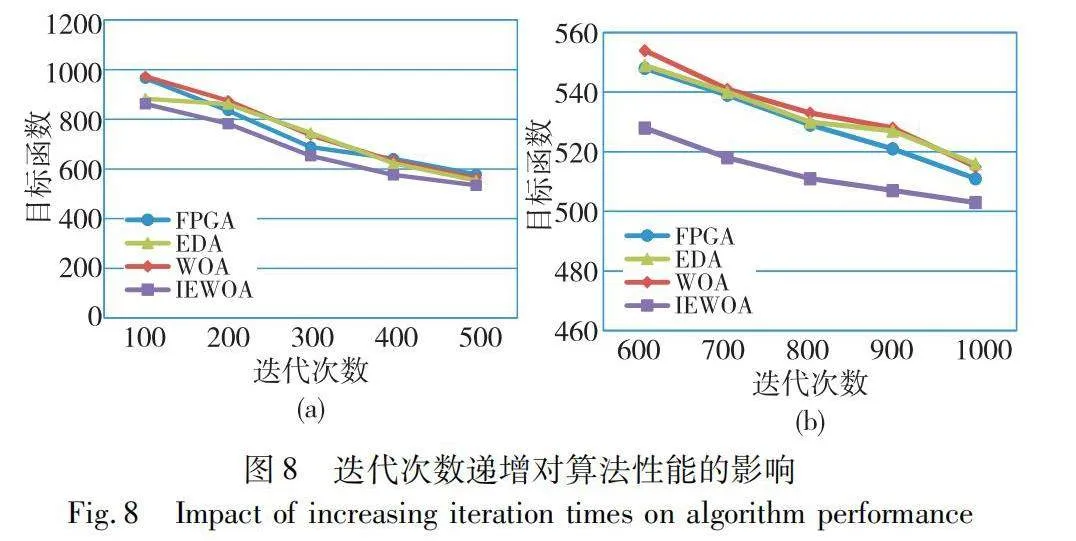
為驗證算法的迭代次數對各算法性能的影響，在處理節點數為3，種群數為10，任務數為60的情況下，改變迭代次數依次100、200、300、400、500情況下各算法的尋優能力對比，具體實驗結果如圖8（a）所示。

初始種群的產生由于隨機性，質量不會隨著迭代次數的改變而發生變化。圖8（a）展示迭代次數對調度結果的影響，IEWOA在迭代次數為100時與EDA尋優能力近似，但隨著迭代次數增加IEWOA較EDA、WOA和FPGA都略勝一籌，并且迭代次數達到500時，四種算法所獲得最優目標函數值非常接近。為進一步驗證迭代對四種算法性能的影響，再一次將迭代次數依次從600每次遞加100直到1 000，具體的實驗結果如圖8（b）所示。

從圖8（b）可以發現，算法的迭代次數600時，FPGA、WOA和EDA三算法所獲得最優目標函數值近似，而IEWOA所獲得最優目標函數值要小于前三種算法。但隨著迭代次數逐漸遞增到1 000時，雖然IEWOA全局尋優的能力都略強于前三種算法，但四種算法都在不斷收斂到全局最優解，而且迭代次數越多四種算法所獲得最優解越近似趨近于全局最優解。這也說明當算法迭代次數足夠時四種算法都會無限逼近全局最優解，但是由于計算資源的有限必然需要限制迭代次數，這樣IEWOA在同等情況下就具有更好的實用價值。

4）算法的執行時間

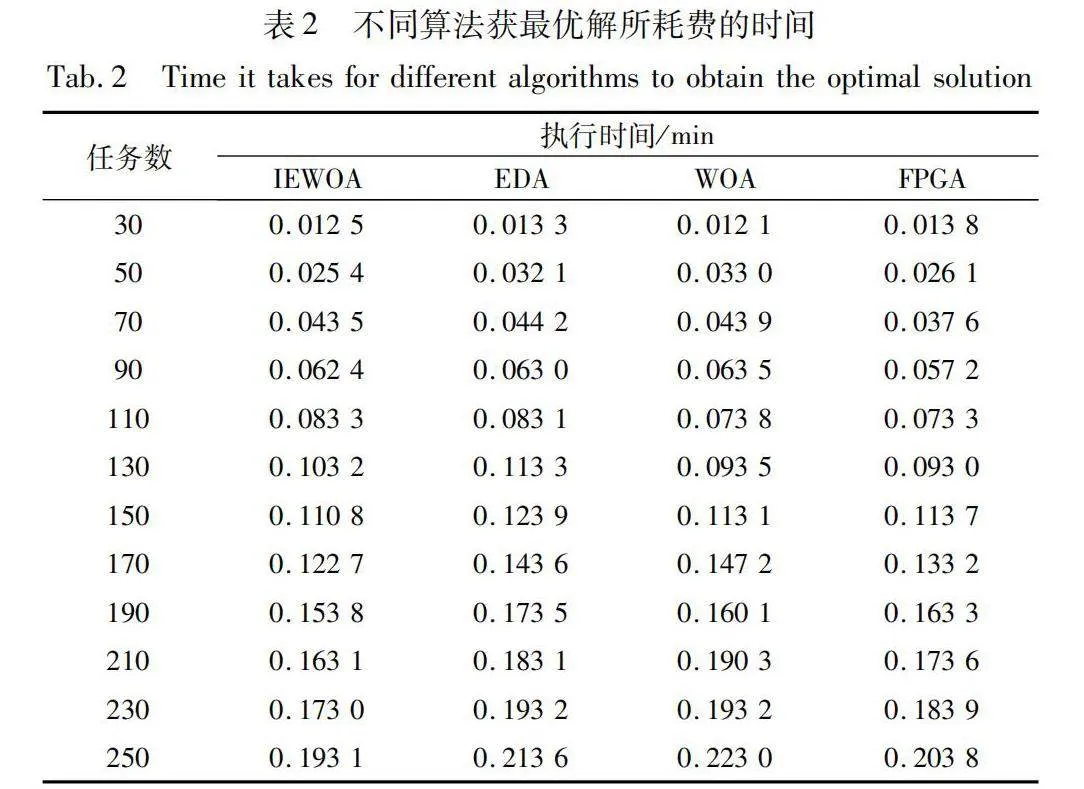
參數設置為處理節點數為3，種群數為10和算法的迭代次數為1 000，比較了IEWOA、EDA、WOA和FPGA四種算法在任務數分別為30、50、70、90、110、130、150、170、190、210、230、250時，獲的最優解所耗費的時間，如表2所示。

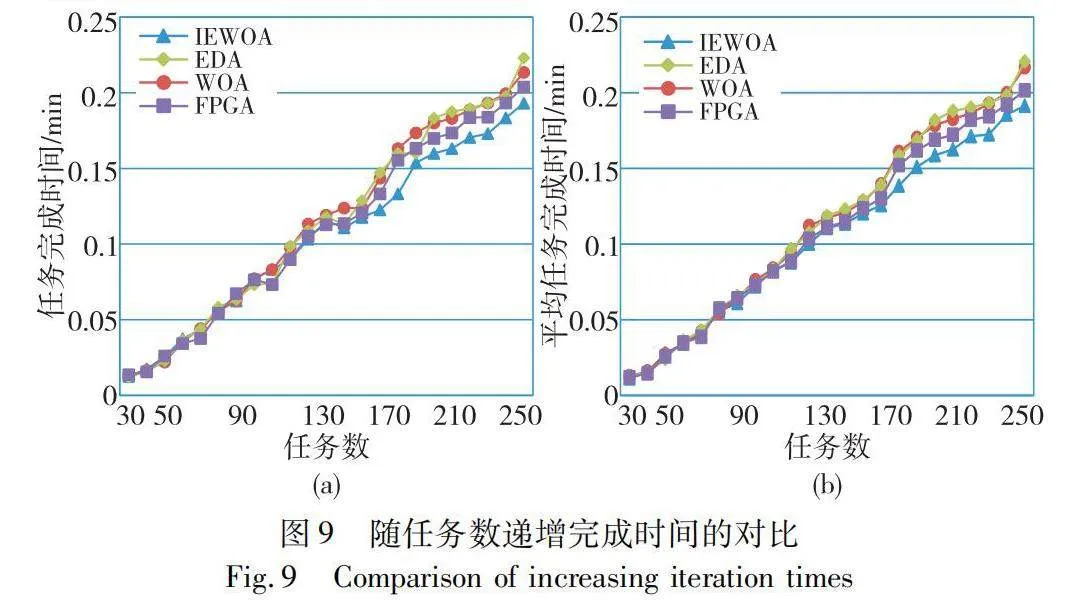
從表2發現在任務數從30遞增到130時，FPGA獲得最優解所耗費的時間要少于IEWOA、WOA和EDA三算法。這說明在任務數較少的情況下，FPGA由于算法變異因子特性獲得不容易陷入局部最優解而能更快地找到全局最優解，而IEWOA、WOA和EDA三種算法耗費時間近似。但是當任務數從150遞增到250時，IEWOA隨著任務數的增大獲最優解所耗費時間較其他三算法都要少，而且隨著任務數的增大這種優勢越明顯，同時FPGA對比傳統EDA和WOA表現又要好一些。通過比較可以發現，IEWOA在前期任務數不多的情況下，算法在尋優方面的性能并不是太明顯而且有時會顯得落后于FPGA，但是隨著任務數和計算量的增加，IEWOA的全局尋優能力和性能優勢就比較突顯。為更全面驗證算法的整體尋優能力和以上分析結果，把實驗設定任務數從30每次遞增10直到250為止，四種算法獲最優解所耗費的時間如圖9（a）所示。

圖9（a）進一步驗證在任務數隨30遞增到100時，四種算法在獲最優解所耗費的時間比較接近，任務數從100到130時，四種算法任務完成獲最優解所耗費的時間開始有所分化，但分化不算明顯，尤其IEWOA、WOA和FPGA三種算法此時性能還比較近似。隨著任務數從130到150再到250，四種算法的性能開始明顯分化，傳統EDA和WOA比FPGA和IEWOA該方面的性能就明顯落后，同時IEWOA的較其他三種算法優勢也逐漸明顯。為避免由于一兩次算法運行可能產生隨機性導致算法驗證不可靠，下面進一步對任務數30到250的實驗反復進行10次，最后總結出四種算法的平均任務完成時間如圖9（b）所示。

圖9（b）驗證任務數從30遞增到110時，在計算平均完成時間下四種算法在獲最優解所耗費的時間非常接近，并且隨任務數的遞增較平穩遞增，此時能避免由于算法隨機初始化數據導致算法性能波動等不良因素。說明計算平均完成時間時四種算法在任務數30～110時性能都比較接近，然后隨著任務數130～250，四種算法的性能開始分化，FPGA和IEWOA的性能優勢開始顯現，傳統EDA和WOA隨著任務數的遞增性能一直比較接近。同時也發現FPGA和IEWOA在任務數130～170的遞增過程中性能近似，IEWOA略優于FPGA。在任務數170～250兩算法的性能優勢開始分化，這時IEWOA明顯開始優于FPGA，充分說明IWEOA具有更好的尋優能力。

4 結束語

總之IEWOA對于解決區塊鏈有向無環圖中的非獨立任務調度問題具有較好的性能，可以為該領域的研究和應用提供有力支持。最后通過仿真實驗，從設置特定參數、改變種群規模、改變迭代次數三方面依次對比了IEWOA與EDA、FPGA、WOA的尋優能力，從而充分地展示了IEWOA的優勢，也說明IEWOA相比于FPGA和WOA的微觀層面的進化方式， 其融入EDA采用基于搜索空間的宏觀層面的進化方式， 從而獲得比其他三種算法更強的全局搜索能力和更快的收斂速度。

參考文獻：

［1］Alladi T， Chamola V， Parizi R M， et al. Blockchain applications for industry 4.0 and industrial IoT： a review［J］. IEEE Access， 2019， 7（1）： 176935-176951.

［2］Hsiao S J， Sung W T. Blockchain-based supply chain information sharing mechanism［J］. IEEE Access， 2022， 10（1）： 78875-78886.

［3］Li Zhi， Barenji A V， Huang G Q. Toward a blockchain cloud manufacturing system as a peer to peer distributed network platform［J］. Robotics and Computer Integrated Manufacturing， 2018， 54（1）： 133-144.

［4］Giungato P， Rana R， Tarabella A， et al. Current trends in sustainability of bitcoins and related blockchain technology［J］. Sustainability， 2016， 9（12）： 1-11.

［5］Elsayeh M， Ezzat K A， El-Nashar H， et al. Cybersecurity architecture for the internet of medical things and connected devices using blockchain［J］. Biomedical Engineering Applications Basis and Communications， 2021， 33（2）： 2150013.

［6］Dorri A， Kanhere S S， Jurdak R， et al. LSB： a lightweight scalable blockchain for IoT security and anonymity［J］. Journal of Parallel and Distributed Computing， 2019， 134（1）： 180-197.

［7］Ravishankar R， Daniel C. Perspectives on emerging directions in using IoT devices in blockchain applications［J］. Internet of Things， 2020， 10（1）： 100079.

［8］Biswas S， Sharif K， Li F， et al. PoBT： a lightweight consensus algorithm for scalable IoT business blockchain［J］. Internet of Things， 2019， 7（3）： 2343-2355.

［9］Mohanty S N， Ramya K C， Rani， S S， et al. An efficient lightweight integrated blockchain（ELIB） model for IoT security and privacy［J］. Future Generation Computer Systems， 2020， 102（1）： 1027-1037.

［10］Huang Junqin， Kong Linghe， Chen Guihai， et al. Towards secure industrial IoT： blockchain system with credit-based consensus mechanism［J］. IEEE Trans on Industrial Informatics， 2019， 15（6）： 3680-3689.

［11］Cui Laizhong， Yang Shu， Chen Ziteng， et al. An efficient and compacted DAG-based blockchain protocol for Industrial Internet of Things［J］. IEEE Trans on Industrial Informatics， 2020， 16（6）： 4134-4145.

［12］Zhou Tong， Li Xiaofeng， Zhao He. DLattice： a permission-less blockchain based on DPoS-BA-DAG consensus for data tokenization［J］. IEEE Access， 2019， 7（1）： 39273-39287.

［13］Yuan Yong， Wang Yuefei. Blockchain and cryptocurrencies： model， techniques， and applications［J］. IEEE Trans on Systems Man amp; Cybernetics Systems， 2018， 48（9）： 1421-1428.

［14］Novo O. Blockchain meets IoT： an architecture for scalable access management in IoT［J］. IEEE Internet of Things Journal， 2018， 5（2）： 1184-1195.

［15］Makhdoom I， Abolhasan M， Abbas H， et al. Blockchain’s adoption in IoT： the challenges， and a way forward［J］. Journal of Network amp; Computer Applications， 2019， 125（1）： 251-279.

［16］Andoni M， Robu V， Flynn D， et al. Blockchain technology in the energy sector： a systematic review of challenges and opportunities［J］. Renewable amp; Sustainable Energy Reviews， 2019， 100（1）： 143-174.

［17］Kotilevets D， Ivanova A， Romanov O， et al. Implementation of directed acyclic graph in blockchain network to improve security and speed of transactions［J］. IFAC-PapersOnLine， 2018， 51（30）： 693-696.

［18］陳紅華， 崔翛龍， 王耀杰. 基于多種云環境的任務調度算法綜述［J］. 計算機應用研究， 2023， 40（10）： 2889-2895. （Chen Honghua， Cui Xiaolong， Wang Yaojie. Summary of task scheduling algorithms based on multiple cloud environments［J］. Application Research of Computers， 2023， 40（10）： 2889-2895.）

［19］Cheng Yuxia， Wu Zhiwei， Liu Kui， et al. Smart DAG tasks scheduling between trusted and untrusted entities using the MCTS method［J］. Sustainability， 2019， 11（7）： 1826.

［20］Gao Chengxi， Lee V， Li Keqin. D-SRTF： distributed shortest remaining time first scheduling for data center networks［J］. IEEE Trans on Cloud Computing， 2021， 9（2）： 562-575.

［21］Xu Jiang， Nan Guan， Xiang Long. Decomposition-based real-time scheduling of parallel tasks on multicores platforms［J］. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems， 2020， 39（10）： 2319-2332.

［22］曹懷虎， 張艷梅， 王堅， 等. DAG區塊鏈中基于確定性退火技術的融合分割遺傳任務調度算法［J］. 中國科學： 信息科學， 2020， 50（2）： 261-274. （Chao Huaihu， Zhang Yanmei， Wang Jian， et al. Fusion-partitioning genetic task scheduling algorithm based on deterministic annealing technology in DAG blockchains［J］. Scientia Sinica： Informationis， 2020， 50（2）： 261-274.）

［23］Mirjalili S， Lewis A. The whale optimization algorithm［J］. Advances in Engineering Software， 2016， 95（5）： 51-67.

［24］Mohamed A， Ei A， Ahmed A， et al. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation［J］. Expert Systems with Applications， 2017， 83（1）： 242-256.

［25］Sun Yanan， Yen G G， Yi Zhang. Improved regularity model-based EDA for many-objective optimization［J］. IEEE Trans on Evolutionary Computation， 2018， 22（5）： 662-678.

［26］Shirazi A， Ceberio J， Lozano J A. EDA+： estimation of distribution algorithms with feasibility conserving mechanisms for constrained continuous optimization［J］. IEEE Trans on Evolutionary Computation， 2022， 26（5）： 1144-1156.

［27］Platel M D， Schliebs S， Kasabov N. Quantum-inspired evolutionary algorithm： a multimodel EDA［J］. IEEE Trans on Evolutionary Computation， 2009， 13（6）： 1218-1232.