基于多層次隨機梯度下降的大規模圖布局算法
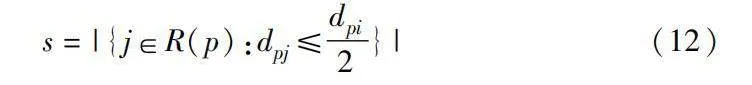
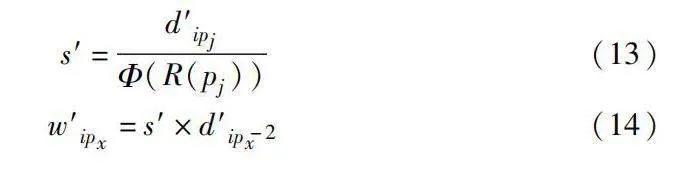


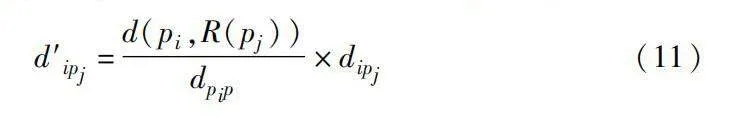


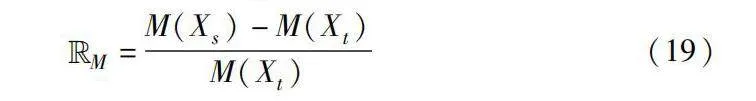

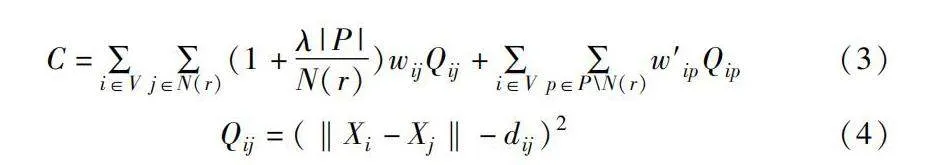


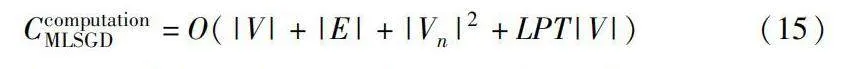
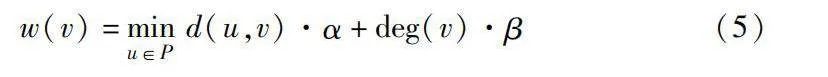

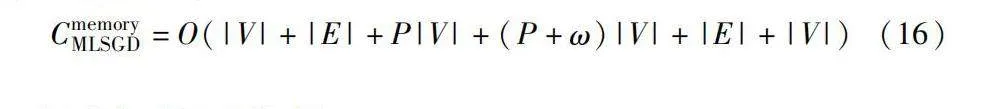

摘 要:大規模圖布局問題是圖可視化領域研究熱點之一。應力布局模型在保持全局布局結構方面表現出色,然而其求解速度卻不及彈簧電荷模型,且局部布局質量也有所欠缺。在維持全局結構穩定條件下,為提高應力模型求解大規模圖時的布局速度、改進布局局部結構表達,提出了一個新的多層次隨機梯度下降圖布局模型。首先利用基于鄰居結構的圖壓縮合并算法生成層次圖結構,再使用節點最優放置算法初始化節點坐標。最后利用融合了節點正負樣本的隨機梯度下降算法細化布局,改進局部布局質量。同時多層次方法也有效提高了布局速度。在30個不同規模的數據集上與現有布局模型進行對比實驗,從布局計算效率、布局質量以及可視化效果三個方面證明了該方法的有效性。
關鍵詞:大規模圖布局;應力模型;隨機梯度下降;多層次布局;圖可視化
中圖分類號:TP391 文獻標志碼:A 文章編號:1001-3695(2024)11-028-3394-07
doi:10.19734/j.issn.1001-3695.2024.03.0073
Large-scale graph layout algorithm based on multi-level stochastic gradient descent
Zhou Yingxin1a, Li Xuejun1a, Wu Yadong2, Zhang Hongying1b, Wang Jiao1b, Zhang Qiumei1a, Wang Guijuan1a, 1b?
(1.a.School of Computer Science amp; Technology, b.School of Information Engineering, Southwest University of Science amp; Technology, Mianyang Sichuan 621000, China; 2.School of Computer Science amp; Engineering, Sichuan University of Science amp; Engineering, Zigong Sichuan 643000, China)
Abstract:Large-scale graph layout remains a prominent focus in graph visualization research. While the stress model excels in representing global structure, its speed lags behind the spring-electric model, and its local structure quality is suboptimal. This paper proposed a graph layout algorithm, aimed at enhancing the efficiency of layout while preserving global structure and improving local quality. The model first utilized graph compression based on neighbor structure to generate a hierarchical graph structure, and then used the node optimal placement algorithm to initialize the node coordinates. Next, it improved the local quality of layout using a SGD layout algorithm based on positive and negative samples, and further enhanced the layout speed through multi-level algorithm. Finally, comparative experiments with existing layout models on 30 datasets of different scales demonstrate the effectiveness of the proposed model in terms of efficiency, layout quality and visualization.
Key words:large-scale graph layout; stress model; stochastic gradient descent; multi-level layout; graph visualization
0 引言
網絡或圖表達對象實體之間的關系,是一種常見的數據結構類型,廣泛存在于多個領域并發揮著重要作用[1,2],例如社會網絡、知識圖譜、生物化學網絡以及神經網絡等。網絡(圖)可視化在信息可視化領域已經成為分析和理解大型復雜網絡隱藏結構的有效工具,其中最有效的是節點連接圖[3,4],它將實體與關系分別建模為節點與節點間的連邊,是描述圖數據整體結構和理解節點間關系的有效方法[2]。節點連接圖的繪制需要一種布局模型根據節點的連接關系計算所有節點合理有效的2維或3維坐標。理想情況下,圖布局算法可以快速執行并產生符合圖布局領域美學標準的布局,例如應力誤差、鄰域相似度和最小角度等指標[5]。然而,隨著數據規模增加至數十萬,布局算法運行時間大幅增加[6],部分算法難以在短時間內獲得結果,若得到在視覺上、美學指標表現較差的布局結果,則無法實現有效可視化。因此,圖布局模型求解大規模圖的速度和產生優秀布局結果的能力對圖可視化任務至關重要[1,4,7]。
本文主要將現有圖布局算法分為彈簧電荷模型[3,6,8,9]、應力模型[10,11]、維度下降類[2,12,13]以及深度學習[14]四類,詳細介紹可參考文獻[7]。應力模型將圖布局問題轉換為了一個優化問題,認為布局節點之間的距離應該等于圖論距離,也被稱為理想距離(ideal length, IL)。該模型主要反映了節點間的整體連接關系,在保持全局結構上效果更好[10]。由于應力模型需計算全對最短路徑長度(all-pairs shortest path,APSP),且傳統求解方法[15,16]時間與空間復雜度高,布局易陷入較差的局部最小化,無法滿足較大規模的圖布局任務。為了提高應力模型的求解速度與質量,Khoury等人[17]提出了基于奇異值分解的low-rank方法實現近似計算APSP。Ortmann等人[18]借助PMDS只計算樞軸頂點和其他頂點之間的距離,減少了計算復雜度。雖然這些模型在一定程度上提升了速度,但受限于基礎求解方法,仍無法用于大規模圖布局。最近,Zheng 等人[10]提出了隨機梯度下降布局方法SGD2,與上述傳統方法相比,能更快收斂且不依賴初始布局,但其最小角度等局部布局優化較差。Xue等人[19]提出的Taurus模型可以轉換應力模型為彈簧電荷模型,使用SGD[10]與BH綜合求解器計算布局,但布局速度仍然較慢。Ahmed等人[20]提出了SGD2布局算法,以線性組合的美學指標為目標函數,使布局結果滿足指定美學要求,但未優化其布局速度。總之,現有應力模型求解方法能有效保持布局全局結構,但更多關注遠距離節點對[3],局部布局質量優化較差,布局時間較長。本文則結合了多層次布局[9]與SGD2[10]算法提升布局速度,并改進了目標函數實現局部質量優化。
多層次布局[9]是一種常用于彈簧電荷模型中提升布局速度與質量的技術,其通過圖聚合算法在原圖基礎上生成一個粗粒度圖,再遞歸壓縮得到多個具有映射關系的粗粒度圖,布局時方向與壓縮階段相反,每次利用前一層次的布局結果進行初始化,逐層細化最終得到原圖布局結果。不同多層次布局方法的主要區別在于使用了不同的分層聚合和布局細化方法,例如FM3[21]使用了類似“太陽系統”的聚合方法,在細化過程中使用BH[22]近似計算頂點間的斥力。DRGraph[2]是一種強調鄰域的維度下降布局模型,使用了一種線性復雜度的分層算法保持全局結構。最近Hong等人[23]提出基于Louvain的快速多層次算法,使用三種力引導算法細化布局。周銳等人[24]提出了一種強調網絡聚類的布局算法,使用基于個性化PageRank的社團劃分算法粗化網絡和基于IL的FR算法細化布局。若將多層次布局算法應用到應力模型,會出現“布局節點抖動”問題,其根本原因是應力模型需要使用IL作為優化目標,而對圖分層會使不同層次中相同節點的IL不一致,優化目標不一致導致了抖動現象發生,并且由于時間復雜度的關系,也無法簡單地通過計算大規模圖的APSP解決。本文則通過基于鄰居結構的圖壓縮合并、新增節點最優放置算法減弱抖動現象。
針對上述應力布局模型中“布局節點抖動”,布局求解時間較長,局部布局質量優化差的問題,本文提出了基于多層次隨機梯度下降的大規模圖布局算法(multi-level stochastic gradient descent algorithm for graph layout, MLSGD)。首先利用基于鄰居結構的圖壓縮合并,將節點及其1階鄰居逐層聚合,防止相鄰層次圖結構劇烈變化,在布局時減少節點抖動增加穩定性。然后利用新增節點最優放置算法,先根據相鄰層次圖直徑縮放布局坐標,減少節點IL差異來減少抖動,再為每個新增節點尋找多個已定位節點,計算節點最優坐標,加快單層布局收斂速度。再利用融合了正負樣本的隨機梯度下降布局細化算法PN-SSGD,通過設計新目標函數強化MLSGD對布局的鄰域結構的關注度,實現局部布局質量的優化。最后利用理想距離與權重修正算法補償布局細化過程中因近似梯度估計丟失的結構信息,使MLSGD在提高布局速度優化局部結構的同時還能維持應力模型在全局結構表達上的穩定性。
綜上所述,本文主要貢獻如下:a)針對應力模型求解速度較慢的問題,提出了MLSGD圖布局算法,解決了“布局節點抖動”問題,提供了一種多層次應力布局模型的解決方案;b)針對應力模型局部布局質量優化較差問題,設計了新的目標函數,提出了PN-SSGD布局細化算法,通過增加正樣本節點鄰域范圍及其約束[10]比例,強化模型對局部結構的關注度; c)設計了詳細的對比實驗評估本文算法在布局速度與質量上的表現,驗證了本文算法的有效性。
1 MLSGD算法框架
MLSGD算法框架如圖1(a)所示,共分為三個階段。a)壓縮合并階段。使用線性時間復雜度的基于鄰居結構的圖壓縮合并算法將圖聚合為規模依次減小的一系列粗粒度圖。b)初始布局階段。首先隨機初始化最頂層粗粒度圖Gn節點坐標,使用SGD2[10]或2.3節描述的PN-SSGD算法細化布局。c)節點插值及布局細化階段。對每一層圖包含兩個步驟: (a)新增節點坐標插值。首先根據相鄰兩層次圖直徑比例縮放上一層的布局結果,然后使用新增節點最優放置算法初始化新增節點坐標,使其迅速到達最終節點位置附近。(b)布局細化。使用本文單層布局算法PN-SSGD細化布局,其利用采集的正負樣本節點中包含的結構信息估計節點梯度并移動節點,通過增大正樣本約束[10]范圍與比例來增強模型對局部結構的關注,提高局部布局質量。算法1為MLSGD的詳細步驟。
算法1 MLSGD布局算法框架
輸入:節點集V={v1,v2,…,vN};邊集E={e1,e2,…,eN};劃分閾值TH。
輸出:節點二維布局坐標Pos={X1,X2,…,XN},Xi=(xi,yi)。
a)對原始圖或新生成的圖層,將節點及其一階鄰居合并成新節點,并計算新邊權重,獲得一系列粗粒度圖Gs={G0,G1,…,Gn},Gi=(Vi,Ei);
b)隨機初始化Gn=(Vn,En)節點坐標,若|Vn|≤TH,使用SGD2細化布局,否則使用PN-SSGD算法;
c)對i=n-1到i=0逐層細化Gi布局,重復執行步驟d)e):
d)將上層布局Posi-1坐標縮放,賦值給Gi中對應的節點,對Gi新增節點t∈Vi-1-Vi利用最優放置算法進行坐標插值;
e)使用本文PN-SSGD布局算法細化Gi=(Vi,Ei)布局;
f)算法達到收斂條件或最大迭代次數時返回Pos。
圖1(b)為數據集data在第三階段的布局實例。經階段1得到了包含初始層的3層網絡,從上至下分別為G2、G1、G0,規模依次增大,第0層為data最終布局結果,從圖中可以看出粗化過程中,網絡結構得到了很好的保留,避免了結構突變。
2 MLSGD算法實現
2.1 基于鄰居結構的圖壓縮合并算法
層次劃分算法是多層次布局算法的重要組成部分。為了減少圖數據層次劃分的時間并保持網絡結構,本文改進了文獻[2]實現了一種具備權重的線性時間復雜度的快速層次劃分算法,避免了同類算法的高時間復雜度或網絡結構變動范圍較大的缺點。圖2解釋了從圖G0生成下一層粗粒度的圖G1示例,詳細過程見算法2。
算法2 基于鄰居結構的圖壓縮算法
輸入:圖G0=(V0,E0),TH=500,γ=0.7。
輸出:一系列粗粒度圖Gs={G0,G1,…,Gn},Gi=(Vi,Ei)。
a)對于當前層Gi,若|Vi|gt;TH,則繼續執行步驟b),否則結束。
b)節點合并階段。對于圖Gi,隨機選擇一個節點vi,m;將vi,m及其未被分配的1階鄰居合并到vi,m并在圖Gi+1中創建新節點si+1,m。
c)若vi,m和vi,n在Gi+1中被分配到同一節點si+1,x,則刪除圖Gi中的邊ei=(vi,m,vi,n)。重復步驟b),直到無法分配節點為止,再執行步驟d)。
d)邊生成階段。遍歷Gi中未刪除的邊,查找端點在Gi+1中對應的聚合節點si+1,u,si+1,v。
e)若si+1,u≠si+1,v,按式(1)計算聚合節點間的權重W(si+1,u,si+1,v)。
f)若|Vi+1|≤γ|Vi|,則執行步驟a),否則結束算法。
W(si+1,u,si+1,v)=min(u,v)∈Ei(d(si,u,u)+d(u,v)+d(v,si,v))(1)
其中:d表示兩節點在Gi中的最短路徑長度。粗化步驟減少了每個層級上的節點數量。然而,當Gi+1的大小非常接近Gi時,層次劃分算法的成本會顯著增加[21]。因此,除了步驟a)設置固定大小的劃分閾值之外,當相鄰層節點數滿足|Vi+1|gt;γ|Vi|時,表示在當前壓縮合并規則下,數據規模不能有效縮減,此時停止劃分。為平衡劃分速度與質量,本文將γ設置為0.7。
2.2 新增節點最優放置算法
本算法應用于節點坐標插值階段中圖Gi+1到Gi的新增節點坐標初始化過程,即圖2的逆向過程。常見的同類方法有重心放置、圓環放置和隨機放置[23],它們沒有考慮節點之間的理想距離,不適用于本模型。文獻[25]提出了一種初始節點放置算法,對Gi中的新增節點,在Gi+1中查找距離最近的3個節點,利用式(2)計算坐標,該算法存在三個問題:a)多個新增節點若屬于同一組節點的鄰居,最終初始化為相同坐標;b)不考慮相對位置得到的3個節點可能使初始位置不準確;c)沒有考慮相鄰層次間相同節點對最短路徑長度差異。為了使新增節點迅速到達最終節點位置附近,減小節點抖動加速布局收斂,本文同時考慮鄰居結構和歐氏距離改進文獻[25]所提節點初始化算法,算法描述如下:
算法3 新增節點最優放置算法
輸入:上一層次圖Gi+1節點坐標Posi+1={X1,X2,…,X|Vi+1|},m=5。
輸出:當前層次圖Gi節點的初始坐標Posi={X1,X2,…,X|Vi|}。
a) 計算圖Gi+1、Gi的直徑φi+1、φi。 /*使用相鄰圖直徑縮放下層坐標*/
b) 計算Posi+1(φi/φi+1),作為Gi對應節點的初始坐標。" /*減少差異*/
c) 對Gi中的新增節點t,在Gi中查找d(t,i)最小的m個已定位節點。
d) 按照如下規則選擇3個節點D={u,v,w};節點u與t直接相連;節點v距離u最遠;節點w距離直線uv最遠。
e) D中節點求解如式(2)得到6個錨點,然后選擇出距離最近的3個錨點得到t的坐標。
f) 重復步驟c)~e),所有新增節點坐標初始化完成時,算法結束。
(xt-xi)2+(yt-yi)2=d(t,i)2(xt-xj)2+(yt-yj)2=d(t, j)2 {i, j}∈D2(2)
其中:d同式(1);x與y為坐標,詳細推導參見文獻[25]。
2.3 基于節點正負樣本的隨機梯度下降布局算法PN-SSGD
為了進一步提升算法的速度與局部布局質量,本文改進了文獻[18]提出的稀疏應力求解模型,設計了新的目標函數,將其用于多層次布局中細化階段。類似于文獻[18],本文將應力模型目標函數拆分為鄰域與非鄰域兩部分,如式(3)(4)所示。
C=∑i∈V ∑j∈N(r)(1+λ|P|N(r))wijQij+∑i∈V ∑p∈P\N(r)w′ipQip(3)
Qij=(‖Xi-Xj‖-dij)2(4)
其中:C的第一部分表示節點的正樣本(r階鄰居)構成的約束項,因子λ用于控制正樣本相對于負樣本的比例,通過(r, λ)調節模型對局部結構的關注度。C的第二部分為節點與負樣本之間P構成的約束項,P通過式(5)生成累計概率分布采集得到,也稱為樞軸點集合,此部分約束項用與保持布局的全局結構。N(r)為某節點的r階鄰居節點集合,wij,w′ip表示兩種節點間權重,dij為節點間圖論距離,d′ip為普通節點i與樞軸節點p理想距離,d′ip與w′ip計算方式將在2.5與2.6節介紹。C的核心是利用單個節點與正負樣本節點的梯度值近似估計其與所有節點的梯度值,再根據該值更新節點坐標。
單個節點的正樣本定義為節點的r階鄰居,r通常取1或2,本文研究發現,正樣本相對于負樣本的數量比例以及r的取值對節點的局部結構布局質量有較強的相關性,可以有效提高邊長變化度和最小角度等質量指標。
對于所有節點的負樣本P節點集合,本文算法使用基于最短路徑長度與度數的累計概率分布采樣得到,計算少量均勻分布在圖空間且度數較大的采樣節點P到其余所有節點的最短路徑長度,可以避免計算APSP,考慮節點度數的原因是在移動非相鄰節點對時,負樣本節點坐標保持不變,有助于減少大度數節點移動次數穩定布局結構。每個節點的采樣權重計算方法為式(5),其中α與β控制采樣依據比例,默認情況下α=0.8,β=0.2,然后對節點權重計算累計概率分布進行采樣,P為已采集的節點集合,d同上,deg(v)為節點度數,默認|P|=200。
w(v)=minu∈P d(u,v)·α+deg(v)·β(5)
目標函數確定后,本文采用類似于文獻[10]的隨機梯度下降求解方法,該方法在每輪迭代中每次隨機選擇一對頂點vi、vj構成的約束wijQij按式(6)(7)進行梯度下降計算,然后如圖3所示沿著相反的梯度方向大小為式(8)更新節點坐標。引入隨機性后,損失能夠較快地降低至較小水平,能夠有效地避免陷入較差地局部最小化。與標準SGD不同的是,式(9)中的η更新步長系數可取較大的值使節點快速移動,設置方法與文獻[10]一致。
?(wijQij)?Xk=4wijr
k=i-4wijrk=j0others(6)
r=‖Xi-Xj‖-dij2Xi-Xj‖Xi-Xj‖(7)
XiXj=XiXj+ΔXiΔXj=XiXj-μr-r(8)
μ=min{η×4wij,1},ηmax=1wmin,ηmin=0.1wmax(9)
2.4 布局收斂條件
為不同規模類型圖數據設計出統一的收斂條件是非常困難的[25],為了平衡布局算法收斂速度與布局質量,考慮到多層次布局的特點,本文根據文獻[10]與實驗經驗為每一層設計出式(10)的收斂規則。在每次迭代中檢測節點移動量Δdisp,δ=0.03×max{[|V|/5×104],30},li為第i層圖,i第i層圖平均邊權重,每層最大迭代次數為20(li/ltotal)。
max‖Δdisp‖lt;δ×li×i(10)
2.5 設置理想距離IL
上述算法雖然減少了計算量,但是也丟失了部分的結構信息。為了補償近似梯度估計丟失的結構信息,本文改進文獻[18]的處理方法。由于每個節點總能找到一個距離其最近的樞軸點p∈P,所有具有相同最近p節點的v∈V被劃分到同一區域R(p),從而將每個樞軸節點p關聯為一組節點R(p)V,它們滿足∪p∈PR(p)=V,R(p1)∩R(p2)=。因此,節點i與R(p)中節點之間的約束就可以近似替換為節點i與樞軸p之間的約束,文獻[18]直接使用dip作為ip的IL,但隨著dip增大,節點i與區域R(p)的應力誤差會變得越來越顯著。本文則是利用i到R(p)的平均圖論距離作為新的IL。但由于本文算法無法得到任意節點i到R(p)中所有節點的圖論距離,所以采用了一種近似的方法求得平均值:首先找到節點i所屬節點pi,然后計算pi到區域R(pj)所有節點的平均最短路徑長度d(pi,R(pj)),再按照式(11)計算得出最終的近似IL。
d′ipj=d(pi,R(pj))dpip×dipj(11)
2.6 移動權重修正
按式(3)進行布局梯度計算時,由于普通節點v與樞軸點p普遍距離較遠,當pN(v,1),需保持p靜止維持布局穩定,再通過調整v的移動尺度補償因p不移動產生的距離誤差。文獻[18]使用參數s設置節點v與p之間的移動權重,取值如式(12)所示,當節點距離p節點較遠時,s可能取到非常大的值(|V|/|P|),使節點移動幅度過大,破壞布局穩定性。
s=|{j∈R(p):dpj≤dpi2}|(12)
為了穩定在多層次布局中節點穩定性,防止在較低層次時布局逐漸收斂時發生大的布局波動,本文改進s參數計算方法為式(13),理論上其最大值處于|P|左右,參數含義同上。最后,按照式(14)設置式(3)中普通節點與樞軸節點之間的權重。
s′=d′ipjΦ(R(pj))(13)
w′ipx=s′×d′ip-2x(14)
2.7 算法復雜度分析
本節將從時間與空間復雜度兩個方面分析算法運行性質。a)時間復雜度。本文算法主要耗時由以下幾個部分組成:壓縮合并階段逐層縮減圖數據規模O(|V|+|E|)、初始布局階段布局初始化O(|Vn|2)或為O(P|Vn|+|En|)、各層節點坐標初始化插值O(|V|)與布局細化階段O(P|V|+|E|),其中|Vn|為頂層圖節點數目,通常較小,可以視為常數時間,L表示層次數量,P為樞軸點Pivots數量,T為迭代次數:
CcomputationMLSGD=O(|V|+|E|+|Vn|2+LPT|V|)(15)
b)空間復雜度分析。本文算法對內存的需求由以下幾個部分構成:存儲經過壓縮合并階段后產生的N個層次圖O(|V|+|E|)、記錄節點間的最短路徑長度矩陣O(P(|V|-1))、存儲細化階段需要使用約束項O(P|V|+|E|)以及保存所有節點的坐標位置O(|V|):
CmemoryMLSGD=O(|V|+|E|+P|V|+(P+ω)|V|+|E|+|V|)(16)
3 實驗與結果分析
3.1 實驗設計
為了驗證本文算法的有效性,與幾個經典的和最近的布局方法在一組圖數據上進行實驗,從布局時間與布局質量上評估了MLSGD算法,所有代碼運行于Intel? CoreTM i5-12400F CPU 32 GB的單核Ubuntu-24 GB虛擬機中。
3.1.1 數據集
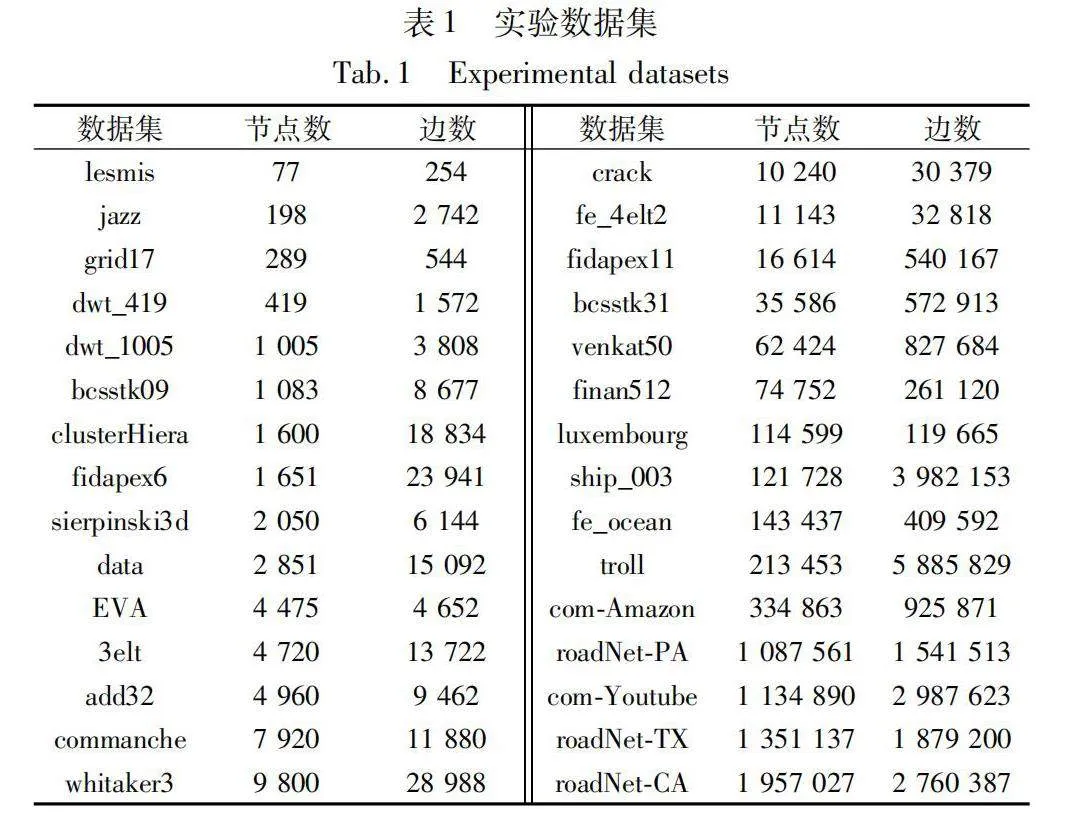
為了實現客觀綜合評價,本文收集了如表1所示常用于同類型文獻[2,3,10,13]的30個具有不同節點和邊數的圖數據,主要選取自Florida Collection[26]、SNAP network Collection[27]以及文獻[2,3]使用的數據。該組數據涵蓋樹圖、網格圖、地鐵、引文和社交網絡等真實世界的圖數據,這些圖的節點數從77到1 957 027,邊數從254到5 885 829。
3.1.2 對比方法
本文選擇了五種圖布局領域較新的和經典算法,它們分別是屬于力模型(force-based)的t-FDP-BH[3]和基于頂點隨機采樣的RVS[6]模型,屬于應力模型(stress-based)的SSGD[10]、最大熵應力布局模型Maxent[28]和GRIP[25]算法。t-FDP-BH和RVS算法使用文獻[3]提供的BH與RVS版本代碼,SSGD、Maxent和GRIP算法的源代碼分別來自文獻[10]、Networkit[29]和Tulip[30]。本文算法參數(r,λ)設置為(1,0),(1,0.3)和(2,0.6)時,分別用MLSGD、MLSGD-N1和MLSGD-N2標識。所有算法都在[-10,10]隨機初始化,參數設置為各自文獻推薦值,所有實驗重復5次以消除隨機性的影響。
3.1.3 評估指標
本文從兩個方面評估算法:a)算法執行效率,對比該算法與其他算法的時間消耗;b)算法有效性,使用應力誤差[28]、鄰域相似度[13]、邊交叉度(crosslessness, CL)[5]、邊長變化度(edge length variation, ELV)[31]和最小角度(minimum angle, MA)[5]五個評估指標和視覺效果綜合評估各算法的布局質量。
3.2 算法效率對比
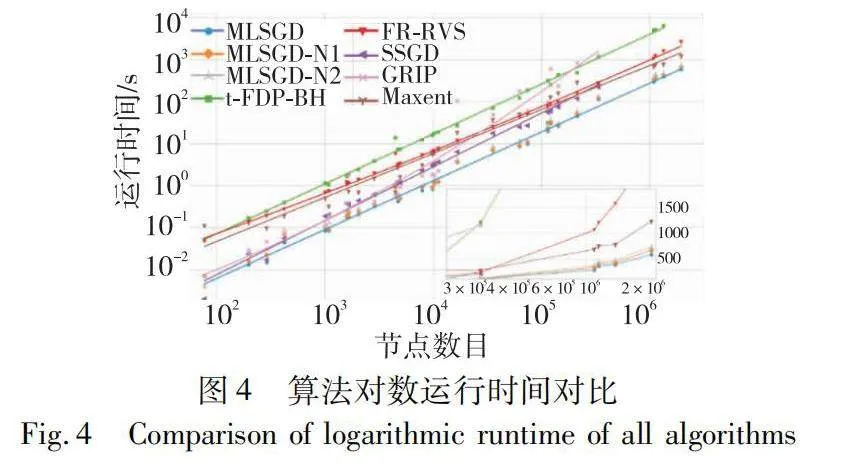
圖4比較了上述算法在所有數據集上的對數運行時間。所有算法只測量布局時CPU占用時間,不包括數據加載等處理步驟。圖中數據缺省項表示由于巨大的內存消耗或計算時間成本導致相應算法無法在有效時間內(lt;7 200 s)獲得結果。
圖4表示運行時間與圖節點數的關系,實線為節點數與時間之間的擬合曲線,其中本文三個不同參數的算法時間消耗非常接近,為減少重疊,只展示了MLSGD的擬合曲線。從圖4可以看出大部分布局模型可以在有效時間內處理所有數據集,布局對數時間同節點數目大致為線性增大關系。從整體上看,除了個別小規模數據集,本文算法MLSGD具有最快的布局速度,由此可見,本文采用多層次布局思想和新增節點最優放置算法能夠有效使節點迅速到達最終位置附近,再結合隨機梯度下降使布局迅速收斂,有效減少了布局時間。使用拉普拉斯變換和BH斥力計算的Maxent與使用頂點隨機采樣的線性FR-RVS算法具有相似的執行效率,但整體上仍然慢于本文算法。GRIP多層次布局算法與SSGD算法在具有少量節點的情況下優于本文算法,這是因為在數據規模較小時,層次劃分與最短路徑長度計算所需時間占總體時間比例較大,但隨著數據規模增大,如圖4中子圖所示,多層次與節點采樣結合的隨機梯度下降布局算法優勢逐漸明顯,計算效率最高可提升至8倍。使用的BH版本t-FDP與RVS類似,固定布局迭代次數,其O(n log n)的時間復雜度導致了其布局最慢。
3.3 布局質量對比
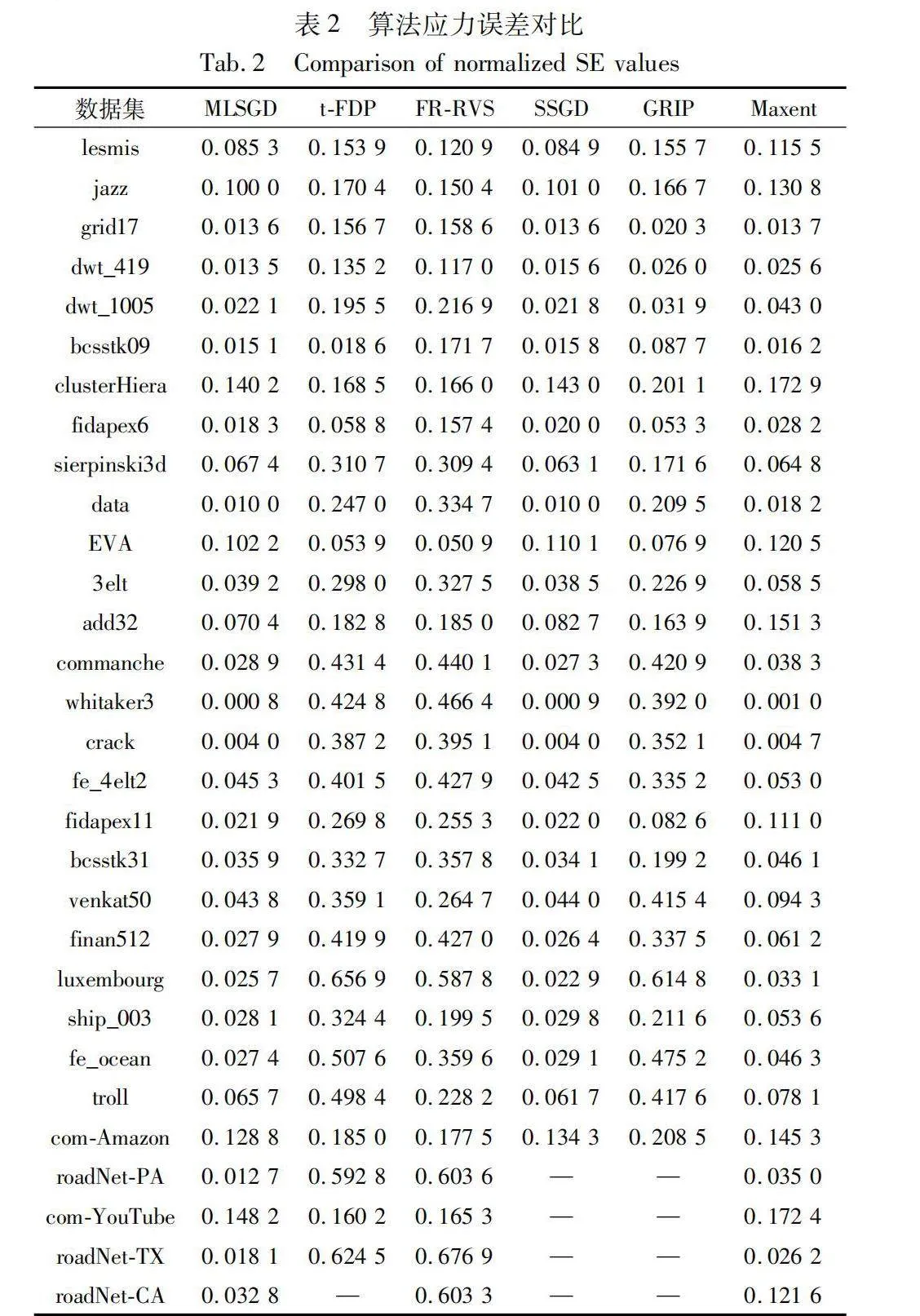
3.3.1 應力誤差(normalized stress error, SE)
SE用于評估一個布局結果的全局結構保持度,其測量圖形布局與理論理想距離的擬合程度。SE定義如下:
SE=2|V|(|V|-1)∑ilt;j(‖Xi-Xj‖-SPD(i, j)2)SPD(i, j)2(17)
其中:dij是節點vi 和vj 之間的最短路徑距離,s是均勻縮放布局的縮放因子,用于不同規模圖數據公平比較。
表2為不同算法在30個圖數據集的SE指標測試結果,加粗值對應的算法在該數據集上全局結構保持最優。從表2可以看出,本文算法在大多數數據集中優于基準算法SSGD,在其他數據集中也與該算法相當,這是因為本文算法采用了多層次的布局思想,從多個層次采集了結構信息用于布局,可以很好地避免陷入局部極小值造成的全局結構損失,同時理想距離與權重修正也有助于算法獲取更精確的全局結構信息。除此之外,SSGD并未提供完全收斂的布局算法,其限制了迭代次數,而本文算法則是設計了一個平衡算法速度與布局質量的收斂條件,最終得到了比SSGD更低的SE值。Maxent會使節點均勻的分布的空間中,這會以犧牲SE值為代價來換取其他布局質量指標的提升。雖然GRIP屬于stress-based算法,但是它在最后一層的布局細化過程中使用了force-based算法,導致其全局結構保持變差。t-FDP-BH與更傾向于關注鄰域結構,布局初始化狀態對其有較大的影響,隨機初始化則加重了這一結果,故SE值普遍較高。FR-RVS除了初始布局狀態原因外,在每輪迭代計算時隨機選擇部分節點進行斥力計算,引入了更多的不確定性,全局結構也保持較差。
3.3.2 鄰域相似度(neighborhood preservation degree, NP)
NP定義為圖空間與布局空間之間的Jaccard相似系數,測量節點的鄰域在布局空間中的保留程度。
NP=1|V|∑i|Ng(gi,r)∩Nl(li,r)||Ng(gi,r)∪Nl(li,r)|(18)
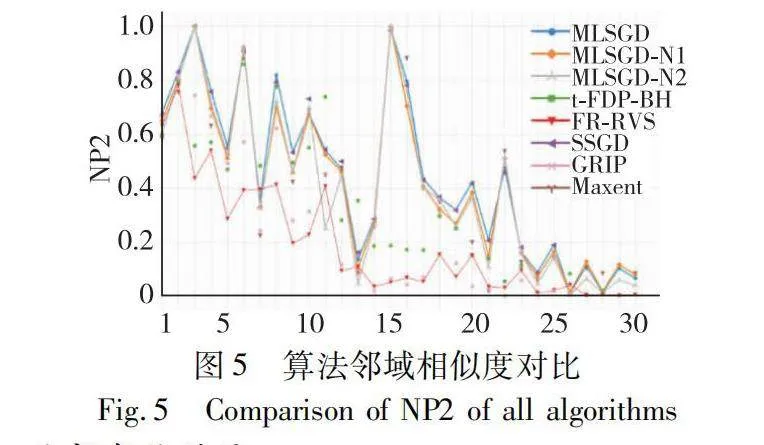
其中:Ng(gi,r)表示節點i在圖空間中的r階近鄰;Nl(li,r)表示節點i在布局空間中的r個最近的鄰居。與文獻[2]一致,本文也用k=2(NP2)來評估鄰域保存的相似性。
圖5比較了所有算法布局結果的NP2值,橫軸為數據集編號,從左至右節點數依次增大,NP2越大表示鄰域保持結果越好。從圖5可以看出MLSGD在將一半的數據集中鄰域保持效果最好,在大部分數據集中都接近最優值,少量數據集中弱于t-FDP-BH和Maxent算法。原因是布局細化過程中,PN-SSGD能夠有效利用正樣本提供的鄰域信息來保持鄰域結構。與SSGD算法相比,本文算法通過多層次的正負節點采樣的方法捕獲了更多樣的局部結構,同時SSGD存在更多關注較遠節點[3]問題,這也是NP2優于SSGD的原因。MLSGD-N1、N2在NP2指標的實驗結果表明調整應力模型關注鄰域與全局結構信息的數量與比例并不能有效解決文獻[3]提出的應力模型在NP2指標保持較差的問題。它們在NP2指標上相較于MLSGD有所下降,在分析了其他布局指標結果(3.3.3節)后,本文發現這兩種算法是以損耗一部分NP2質量的形式優化了其他的局部結構,這也是文獻[20]所提到的難以同時優化的結構案例。對t-FDP-BH隨機初始化節點坐標,即使擁有關注鄰域的特殊力形式,其NP2仍然表現較差。圖中紅色實線表明RVS很難保持較好的鄰域結構。
3.3.3 局部布局質量
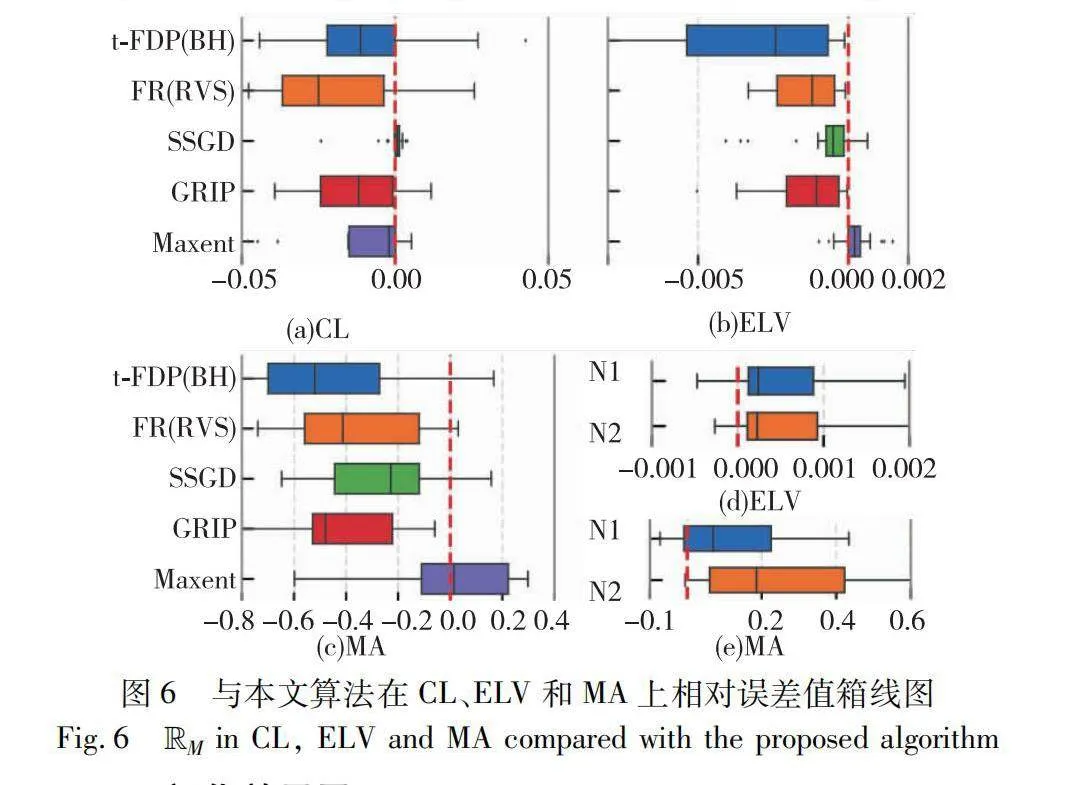
在本節中,將計算其他算法與本文算法在CL[5]、ELV[31]和MA[5]指標上的相對值式(19)。CL表示邊相交的程度,ELV是有效衡量布局質量的美學標準之一,MA計算每個節點實際最小角與理想最小角之間的平均偏差,以上每個指標本文都計算其歸一化值,相對值大于0時(紅色豎線)則表示Xs代表的算法在該指標上越優秀。對于CL及ELV,經過歸一化計算后值即便非常接近,也有較大視覺差異。
從圖6(a)可以看出,本文MLSGD與SSGD在CL指標上效果基本持平,邊交叉數量較少,與其余四種算法對比中,超過3/4的數據本文算法都表現更好。圖6(b)比較了本文MLSGD-N1,可以看出Maxent在ELV指標中表現最好且略優于本文算法,布局結果邊長長度較為統一,布局美觀,而本文算法比包含SSGD在內的算法表現更好,說明增加1階鄰域信息在迭代過程中的比例能夠有效改善局部結構。從圖6(c)可看出,Maxent在MA指標中將近一半的數據集上優于本文MLSGD-N2,節點最小入射邊角度更大,布局更加美觀,而本文算法在增大鄰域范圍后(r=2)也有效改進了原算法SSGD在MA上的布局結果,說明在布局過程中增加鄰域范圍及其約束比例能夠有效改進局部布局結構。圖6(d)(e)分別顯示了本文算法設置不同參數(1,0.3)和(2,0.6)后與設置默認參數(1,0)的MLSGD在ELV和MA指標中的相對誤差值,結果表明,擴大正樣本鄰域范圍與約束比例能夠有效改善局部布局質量。
3.4 可視化效果展示
圖7展示六種算法的布局效果。其中force-based類型算法t-FDP-BH和FR-RVS算法可視化效果較差,一方面原因是節點數目的增多,算法也越來越難以解開圖結構,布局結果較雜亂,另一方面,此類模型依賴初始布局的缺點也變得明顯。luxembourg是現實道路網絡拓撲數據,與MLSGD布局效果相比,可見兩個算法均沒能維持全局結構。本文MLSGD與SSGD可以產生類似的布局結果,節點分布均勻,能夠清晰觀察到局部連接結構,全局結構也保持得更好,保持了較好的對稱性。Maxent在sierpinski3d得到了另一種結構的布局結構,這與其盡量使節點均勻分布的特性相符合,在finan512數據集上則產生了較多的邊交叉,局部結構維持較差,其他三個圖則產生了與本文類似的布局結構。
4 結束語
本文提出了一個新的面向大規模圖的布局算法,提供了一種多層次應力布局模型的解決方案,用以實現大規模圖的快速布局計算,維持布局全局結構的同時提高局部結構質量。該算法有基于啟發式隨機梯度下降的多層次布局算法和基于節點正負樣本的隨機梯度下降單層布局算法兩個主要的創新點。MLSGD通過多層次布局與啟發式隨機梯度下降提高布局速度并維持全局結構,還可調整節點正樣本捕獲的鄰域結構,增加正樣本約束比例,使布局模型關注更多的鄰域信息,從而改善算法的局部布局質量。實驗結果表明,本文算法有效提高了布局算法完成大規模圖布局任務的計算速度,并生成了與SSGD視覺上類似的布局結果,同時優化了最小角度等局部布局效果。除此之外,與其他經典和最新的算法相比,在布局速度、全局結構保持和局部鄰域保持等其他局部質量指標上都有不同程度的領先。盡管本文算法在大規模圖布局問題中具有高效性和可靠性,但未來也存在一些進一步優化的工作,首先現有布局收斂規則是依據實驗經驗設定的,未來將根據不同類型圖數據的特征設計自適應布局收斂規則。除此之外,還會考慮基于GPU并行計算進一步提升本文算法的計算速度。
參考文獻:
[1]Alkadi M, Serrano V, Scott-Brown J, et al. Understanding barriers to network exploration with visualization: a report from the trenches [J]. IEEE Trans on Visualization and Computer Graphics, 2022, 29(1): 907-917.
[2]Zhu Minfeng, Chen Wei, Hu Yuanzhe, et al. DRGraph: an efficient graph layout algorithm for large-scale graphs by dimensionality reduction [J]. IEEE Trans on Visualization and Computer Graphics, 2020, 27(2): 1666-1676.
[3]Zhong Fahai, Xue Mingliang, Zhang Jian, et al. Force-directed graph layouts revisited: a new force based on the t-distribution [J]. IEEE Trans on Visualization and Computer Graphics, 2023,30(7):3650-3663.
[4]楊卓, 謝雅淇, 陳誼,等. 圖可視化布局方法最新研究進展綜述 [J]. 計算機工程與應用, 2023, 59(16): 1-15. (Yang Zhuo, Xie Yaqi, Chen Yi, et al. A review of the latest research progress of graph visualization layout methods [J]. Computer Engineering and Applications, 2023, 59(16): 1-15.)
[5]Purchase H C. Metrics for graph drawing aesthetics [J]. Journal of Visual Languages amp; Computing, 2002, 13(5): 501-516.
[6]Gove R. A random sampling O(n) force-calculation algorithm for graph layouts [J]. Computer Graphics Forum, 2019, 38(3): 739-751.
[7]Zhang Shuhang, Xu Ruihong, Quan Yining. Large graph layout optimization based on vision and computational efficiency: a survey [J]. Visual Intelligence, 2023, 1(1): 14.
[8]Fruchterman T M J, Reingold E M. Graph drawing by force-directed placement [J]. Software: Practice and Experience, 1991, 21(11): 1129-1164.
[9]Walshaw C. A multilevel algorithm for force-directed graph drawing [C]//Proc of the 8th International Symposium on Graph Drawing. Berlin: Springer, 2001: 171-182.
[10]Zheng J X, Pawar S, Goodman D F M. Graph drawing by stochastic gradient descent [J]. IEEE Trans on Visualization and Computer Graphics, 2018, 25(9): 2738-2748.
[11]薛明亮. 圖可視化節點布局與邊捆綁優化問題研究 [D]. 濟南:山東大學, 2023. (Xue Mingliang. Research on graph visualization node layout and edge binding optimization [D]. Jinan:Shandong University, 2023.)
[12]Rahman M K, Sujon M H, Azad A. Scalable force-directed graph representation learning and visualization [J]. Knowledge and Information Systems, 2022, 64(1): 207-233.
[13]Kruiger J F, Rauber P E, Martins R M, et al. Graph layouts by t-SNE [J]. Computer Graphics Forum, 2017, 36(3): 283-294.
[14]劉小芝. 基于圖神經網絡的圖布局評估與生成研究 [D]. 杭州:杭州電子科技大學, 2023. (Liu Xiaozhi. Research on graph layout evaluation and generation based on graph neural network [D]. Hangzhou: Hangzhou Dianzi University, 2023.)
[15]Kamada T, Kawai S. An algorithm for drawing general undirected graphs [J]. Information Processing Letters, 1989, 31(1): 7-15.
[16]Gansner E R, Koren Y, North S. Graph drawing by stress majorization [C]//Proc of the 12th International Symposium on Graph Drawing. Berlin: Springer, 2005: 239-250.
[17]Khoury M, Hu Yifan, Krishnan S, et al. Drawing large graphs by low-rank stress majorization [J]. Computer Graphics Forum, 2012,31(3pt1): 975-984.
[18]Ortmann M, Klimenta M, Brandes U. A sparse stress model [C]// Proc of International Symposium on Graph Drawing and Network Visua-lization. Cham: Springer International Publishing, 2016: 18-32.
[19]Xue Mingliang,Wang Zhi,Zhong Fahai, et al. Taurus: towards a unified force representation and universal solver for graph layout [J]. IEEE Trans on Visualization and Computer Graphics, 2022, 29(1): 886-895.
[20]Ahmed R, De Luca F, Devkota S, et al. Multicriteria scalable graph drawing via stochastic gradient descent, (SGD)2 (SGD)2 [J]. IEEE Trans on Visualization and Computer Graphics, 2022, 28(6): 2388-2399.
[21]Hachul S, Jünger M. Drawing large graphs with a potential-field-based multilevel algorithm [C]//Proc of International Symposium on Graph Drawing. Berlin: Springer, 2004: 285-295.
[22]Barnes J, Hut P. A hierarchical O(N log N) force-calculation algorithm [J]. Nature, 1986, 324(6096): 446-449.
[23]Hong S H, Eades P, Torkel M, et al. Louvain-based multi-level graph drawing [C]// Proc of the 14th IEEE Pacific Visualization Symposium. Piscataway,NJ:IEEE Press, 2021: 151-155.
[24]周銳, 王桂娟, 鄧皓天,等. 復雜網絡聚類特征層次布局算法 [J]. 計算機應用研究, 2022, 39(2): 479-484. (Zhou Rui, Wang Guijuan, Deng Haotian, et al. Hierarchy clustering characte-ristics of complex network layout algorithm [J]. Application Research of Computers, 2022, 39(2): 479-484.)
[25]Gajer P, Kobourov S G. GRIP: graph drawing with intelligent placement [J]. Journal of Graph Algorithms and Applications, 2004, 6(3): 203-224.
[26]Davis T A, Hu Yifan. The University of Florida sparse matrix collection [J]. ACM Trans on Mathematical Software, 2011, 38(1): 1-25.
[27]Leskovec J, Krevl A. SNAP datasets: Stanford large network dataset collection [DB/OL]. (2014). https://snap.stanford.edu/data/.
[28]Gansner E R, Hu Yifan, North S. A maxent-stress model for graph layout [J]. IEEE Trans on Visualization and Computer Gra-phics, 2012, 19(6): 927-940.
[29]Staudt C L, Sazonovs A, Meyerhenke H. NetworKit: a tool suite for large-scale complex network analysis [J]. Network Science, 2016, 4(4): 508-530.
[30]Auber D, Archambault D, Bourqui R, et al. TULIP 5 [EB/OL]. (2017). https://tulip.labri.fr/site/.
[31]Kieffer S, Dwyer T, Marriott K, et al. Hola: human-like orthogonal network layout [J]. IEEE Trans on Visualization and Computer Graphics, 2015, 22(1): 349-358.
[32]Miller J, Huroyan V, Kobourov S. Spherical graph drawing by multi-dimensional scaling [C]//Proc of International Symposium on Graph Drawing and Network Visualization. Cham: Springer International Publishing, 2022: 77-92.

