基于二維動態元胞自動機的偽隨機耦合映像格系統及其動態特性

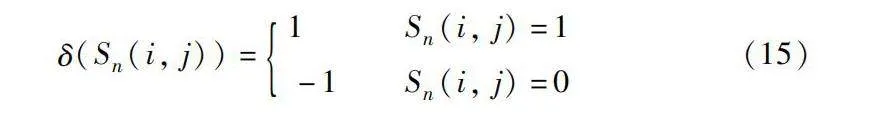
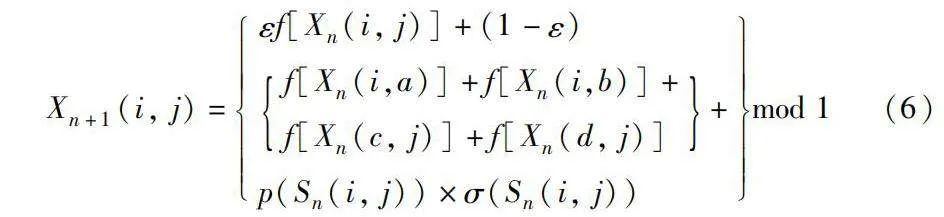
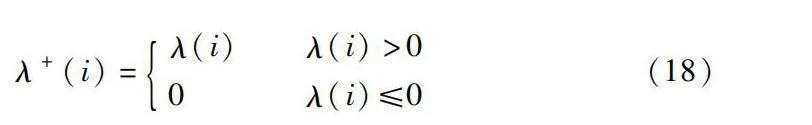
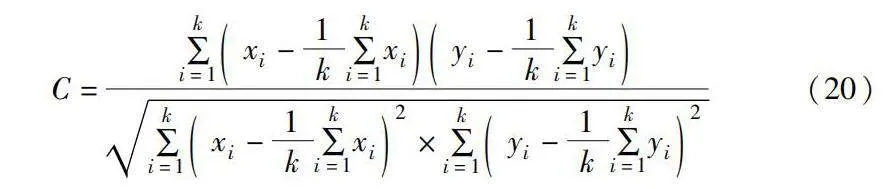
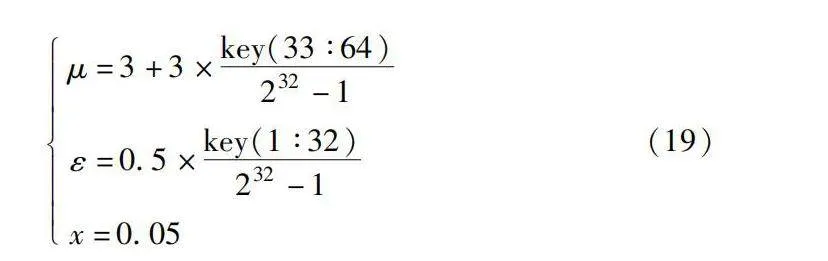
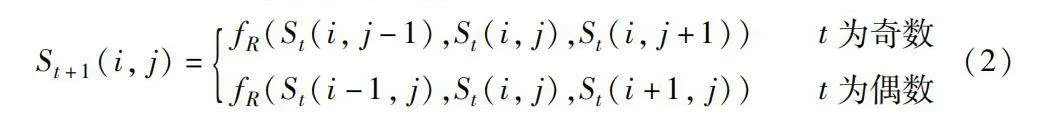
摘 要：針對時空混沌系統中遇到的混沌強度不足等問題，提出了一種基于二維動態元胞自動機的偽隨機耦合映射格系統方案。基于初等元胞自動機，設計了二維動態元胞自動機，通過變換其迭代次數，動態選取迭代規則和方向，實現狀態的多樣性更新，從而增強了元胞的偽隨機特性。在每次元胞狀態更新時，根據格子所對應元胞的行和列位置動態生成耦合索引值，并利用索引值對混沌序列施加擾動提升序列的隨機性，降低了格子之間的相關性。對系統動力學特性進行分析，發現其有較強的混沌特性和隨機性，能夠有效延長系統的周期，增強遍歷性。最后，利用SHA-256運算生成混沌系統初始化參數，結合系統的輸出序列和DNA編碼設計出一種圖像加密算法，并對該算法進行信息熵等性能分析。實驗結果表明，該算法加密結果擁有較好的統計特性和安全性，在圖像加密領域有較好的應用前景。

關鍵詞：混沌；二維元胞自動機；二維耦合映像格；圖像加密

中圖分類號：TP391.9 文獻標志碼：A 文章編號：1001-3695（2024）11-029-3401-08

doi：10.19734/j.issn.1001-3695.2024.04.0079

Pseudo random coupled image lattice system based on two dimensional dynamic cellular automata and its dynamic characteristics

Ma Yingjie^a， Hong Hui^b?， Zhang Lei^a， Liu Yaqi^c

（a.Dept. of Electronic amp; Communication Engineering， b.Dept. of Cyber Space Security， c.Information Security Institute， Beijing Electronic Science amp; Technology Institute， Beijing 100070， China）

Abstract：This paper proposed a pseudorandom coupled mapping lattice system scheme based on two-dimensional dynamic cellular automata to address the issue of insufficient chaos intensity in spatiotemporal chaotic systems. It designed the two-dimensional dynamic cellular automata based on elementary cellular automata， which achieved state diversity update through varying iteration counts and dynamically selecting iteration rules and directions， thereby enhancing the pseudorandom properties of the cells. During each cell state update. It dynamically generated coupling index values based on the row and column positions of the corresponding cells， and used these index values to perturb the chaotic sequences， improving their randomness and reducing correlations between cells. Analysis of the system’s dynamic characteristics revealed strong chaos and randomness， effectively extending the system’s period and enhancing ergodicity. Finally， this paper designed an image encryption algorithm using SHA-256 operations to generate initialization parameters for the chaotic system， combined with the system’s output sequence and DNA encoding. Performance analysis of the algorithm， including information entropy， show that it possesses good statistical properties and security， promising good application potential in the field of image encryption.

Key words：chaos; two dimensional cellular automata; two dimensional coupled mapping lattice; image encryption

0 引言

混沌現象指的是，在一個確定的動力學系統中，會展現出似乎隨機、不規律的行為。這種現象的特征包括無序性、復雜性以及非周期性的表現形態。這種動力學現象具有確定性和隨機性的結合，使得系統的行為呈現出無法準確預測的特征。混沌系統因其獨特的性質而備受關注，其中包括偽隨機性、對初始條件的高度敏感性、遍歷性和不可預測性等密碼學特征。然而，當混沌系統在數字計算機上以有限精度運行時，存在著動力學退化的問題，即使在理論上具有非周期性，但實際上卻不能產生真正的隨機序列。這一困境促使了對混沌系統的進一步研究，尤其是在提高其偽隨機性和動態特性方面的探索。

為了克服混沌系統的動力學退化問題，研究人員提出了多種解決方案，包括采用更高精度的數字系統^［1］、級聯多個混沌系統以增加其周期性^［2］、以及添加擾動以改善系統的動態特性^［3］等。盡管這些方案在一定程度上能夠改善系統的性能，但仍然存在著資源浪費、動態復雜性下降等問題。

通過空間耦合和混沌輸出相互作用，時空混沌系統有效減緩了動力學衰退。在文獻［4，5］創立了基于混沌系統的耦合映射格（coupled map lattices，CML）后，眾多CML混沌系統被開發出來^［6～9］。

以基于logistic映射的CML時空混沌系統為例，其中任意格子的輸出主要聚集在0和1附近，CML系統的回歸映射呈固定拋物線形狀。攻擊者利用該特征推斷系統的控制參數，可能進行回歸映射和相空間重構攻擊^{［10，11］}。混沌系統的底層映射中，特定控制參數可能導致弱混沌狀態。文獻［7］引入分數階混沌映射，仍展現周期窗口和弱混沌。文獻［12～14］嘗試動態耦合和非線性耦合等方法，弱混沌和周期窗口依然存在，輸出序列的分布仍不均勻，而回歸映射仍然主要集中在拋物線附近。文獻［15］基于其提出的PWLCM-Sin映射構建了新型的時空混沌系統，該系統利用系統本身生成的序列實現了偽隨機耦合，系統擁有較少的周期窗口，良好的混沌特性。然而，該混沌系統的輸出依舊沒有擺脫底層映射的影響，回歸映射分布依舊集中在PWLCM映射所特有的三角波形上，依舊易受到回歸映射分析的攻擊。從耦合方案的角度分析，傳統的CML采用鄰近耦合，能量傳遞慢，部分格子無法達到混沌。Zhang等人^［7］提出的非線性耦合方案，提高了傳輸速度，但格子之間的耦合仍保持不變。混合線性-非線性方案^［13］加快了能量傳遞，但仍有弱混沌狀態。

針對初等元胞自動機短周期性的問題，本文提出了一種二維動態元胞自動機（two-dimensional dynamic elementary cellular automata， TDECA）。根據迭代次數不同，動態選擇迭代方向和規則，每次更新不同的元胞狀態值，TDECA能夠在迭代過程中產生更加復雜的演化規律，從而改善系統的長期周期性和提高偽隨機性。

基于TDECA設計了一種新的耦合方案。該模型利用TDECA的輸出狀態確定各個格子對應的耦合索引值，并根據格子坐標對應元胞水平、豎直方向的擾動值對系統進行動態擾動。這種動態的耦合機制進一步削弱時空混沌系統的動力學退化，有效增加了系統的動態復雜性，并提升了能量傳遞效率。

仿真實驗結果表明，所提二維動態偽隨機耦合映像格系統具有更復雜的動力學特性和更好的隨機性，能夠在同等條件下生成更多的偽隨機序列，增加了系統的不確定性，使得系統更難以被攻擊者預測和破解，從而提高了系統的安全性和可靠性。因此，該系統在密碼學和混沌保密通信領域具有廣泛的應用前景，為混沌系統在實際應用中的進一步發展提供了新的思路和方法，在提高系統的安全性和可靠性，以及推動混沌系統在密碼學和信息安全領域的應用具有重要意義。

1 二維動態元胞自動機

Neumann等人^［16］在1948年提出的元胞自動機（cellular automata， CA），其是一個用于最初模擬生物系統自我復制行為的離散動力學系統。作為元胞自動機的一種簡化版本，初等元胞自動機（clementary cellular automata， ECA）由一維元胞排列組成，常用周期邊界，使得序列首尾元胞相連。

元胞的未來狀態由其本身及其周圍相鄰元胞的當前狀態共同決定，此方法既簡明又高效，且適合并行處理^［17］。Wolfram將這些變化規則歸納為簡單、周期性、混沌和復雜規則^［18］四類。隨著研究發展，眾多學者提出了基于CA的多樣化加密方法^［19］。

ECA是最廣泛使用的一種一維元胞自動機模型，其定義可通過式（1）表達。

S_n=（A^N，Σ，f，E）（1）

在這個模型中，定義了元胞空間A^N、空間維度N、狀態值Σ（通常為0或1）、更新規則f以及邊界條件E（通常為周期邊界）。狀態更新值s_n也得到了定義。此外，在ECA系統中，元胞在更新狀態時會同時考慮自己當前的狀態和兩側相鄰元胞的狀態。圖1展示了一個具有L個元胞的ECA，該ECA采用了周期性邊界條件。

Wolfram的研究展示了，在一種只有兩種狀態（0和1）且每個元胞由三個鄰居節點決定的一維CA設置中，識別出了256個獨特的演化規則。這些規則根據它們的映射特性進行編號，而狀態更新函數f的結果以十進制數表示，用于區分各個ECA規則的編號。例如，具有編號105（其二進制形態為01101001）的ECA規則的映射如表1所示。

針對初等元胞自動機短周期性的問題，提出了一種二維動態元胞自動機（two-dimensional dynamic elementary cellular automata， TDECA），可以表示為

S_t+1（i， j）=f_R（S_t（i， j－1），S_t（i， j），S_t（i， j+1））

t為奇數

f_R（S_t（i－1， j），S_t（i， j），S_t（i+1， j）） t為偶數 （2）

其中：TDECA的迭代規則R根據迭代次數t控制切換。其迭代方向也由迭代次數t所確定，t為奇數時，各元胞逐行進行迭代，t為偶數時，元胞逐列進行迭代。

為防止TDECA出現短周期性，R應選擇全局混沌規則。以105號和150號規則為例，R確立方式如下：

R=105

Num為奇數150

Num為偶數（3）

2 時空混沌系統設計

耦合映射格系統作為一種時空混沌系統，有助于減緩混沌系統中的動力學退化并增加系統復雜度。在傳統的耦合映射格系統（coupled map lattices， CML）模型中，一個格子的狀態由自身和相鄰格子的狀態共同決定^［20］。公式定義如下：

X_n+1（i）=（1－ε）f［X_n（i）］+ε2{f［X_n（i－1）］+f［X_n（i+1）］}（4）

其中：n表示系統時間維度（n=1，2，3，…）；i表示系統空間維度（i=1，2，3，…，L）；L為系統中總的格子數量。系統的邊界條件是周期的，即：第L個格子為第1個格子的左鄰格子，第1個格子為第L個格子的右鄰格子，ε（0lt;εlt;1）表示系統的耦合強度，映射f（x）通常采用一維logistic映射，其公式如下：

f（x）=μx（1－x）

x∈（0，1）（5）

其中：μ（0lt;μ≤4）為控制參數，當3.57lt;μ≤4時系統處于混沌狀態。

傳統的CML系統對初始條件和參數的微小變化非常敏感，采用鄰近耦合方式，缺乏動態調節機制。這種使得能量傳遞速度較慢，在某些控制參數下仍可能表現出弱混沌狀態導致空間上的一些格子無法達到混沌狀態。

與單一混沌系統相比，CML系統中每個格子內部的混沌系統并行運行。格子間的耦合作用促使能量在不同系統之間流動。由于這種耦合作用，整個系統在時空維度上展現出了混沌的狀態，同時可以生成混沌序列，從而產生大量數據，滿足多種應用需求。系統的耦合參數、控制參數以及每個格子的初始值都可以作為密鑰，顯著擴展了系統的密鑰空間。每個格子的初始值可以不同，由于混沌系統本身的初始值敏感性以及耦合關系，整個系統呈現出更加復雜的動力學特性，相應的混沌特性得到了顯著增強。

CML時空混沌系統表現優越，因其局部混亂與整體穩定特性，使輸出序列和回歸映射軌跡可辨且穩定。但是時空混沌系統在某些參數下存在弱混沌的情況；時空混沌系統的輸出分布不均，特別是在相空間和回歸映射上的分布具有顯著的可識別性；各個格子的輸出相關性較強，由此帶來的安全上的潛在問題。根據Li等人^［21］對這些方法的數學和理論分析，添加隨機擾動是最為有效的方式，包括擾動系統的輸入、輸出及控制參數，其中擾動混沌系統的輸出是最優的。不同格子之間的輸出借助耦合的方式對混沌映射進行擾動，從而有效削弱混沌系統中的動力學退化問題^［22］。

而由于元胞自動機結構和變化的相似性，將元胞自動機和時空混沌系統相結合已經成為加密特別是圖像加密領域的重要研究方法。ECA中的各格子的構成與時空混沌系統CML中的格子具有空間上的兼容性，可以利用ECA來對CML中的各格子施加擾動。ECA本身是一個時間和空間上均離散的系統，因此不會存在動力學退化的問題，全局混沌規則控制下的ECA輸出又具有長周期和偽隨機性，非常適合嵌入到混沌系統中作為擾動，進一步減弱動力學退化的問題，提高系統的隨機性。全局混沌規則下的ECA迭代過程是非單射布爾函數，具有良好的非線性和不可逆性，同時在初始值和迭代規則已知的情況下又是可復現的，適用于分組密碼算法。利用ECA生成的擾動可對不同格子施加不同的擾動，從而降低系統中各格子之間由于耦合存在的高相關性。

因此，結合元胞自動機的時空混沌系統在防止單一時空混沌動力學特性退化的研究上具有巨大潛力，同時憑借高度的并行性和易編程性，對提升圖像加密效率也頗有優勢。

基于以上概念，本文引入了一個新型的二維動態元胞自動機偽隨機耦合映射格系統（two dimensional dynamic pseudo-random coupled map lattices， 2D-DPCML），其數學表達式為

X_n+1（i， j）=εf［X_n（i， j）］+（1－ε）

f［X_n（i，a）］+f［X_n（i，b）］+f［X_n（c， j）］+f［X_n（d， j）］+

p（S_n（i， j））×σ（S_n（i， j））mod 1（6）

其中： f為logistic映射；ε（0lt;εlt;1）用于表示系統的耦合強度；i和j（取值為1～L）代表格子的坐標；n表示時間維度；索引值a、b、c、d是TDECA迭代得到的。這個過程產生的擾動p（S_n）源自TDECA中元胞在水平和垂直方向狀態的變化，當前擾動的符號表示為σ（S_n（i， j））（數值大小±1），擾動值應用mod 1操作，結果保留小數部分，使得最終的運算結果保持在（0，1）。以下是各個參數的詳細計算過程。

2.1 索引方式

TDECA的元胞空間設為100×100，2D-DPCML大小為L×L，采用周期型邊界，在每次更新過程中，二者的格子空間能夠相匹配，耦合對象上、下、左、右四個方向索引值a，b，c，d的確立方式可由式（1）～（12）確立。

（a，b，c，d）=find_index（L_x，L_y，i， j）（7）

（L_x，L_y）=find（i， j）（8）

a=L_x

0lt;L_xlt;LLL_x=01L_x=L（9）

b=L－L_x

0lt;L_xlt;L1L_x=0LL_x=L（10）

c=L_y

0lt;L_ylt;LLL_y=01L_y=L （11）

d=L－L_x

0lt;L_ylt;L1L_y=0LL_y=L（12）

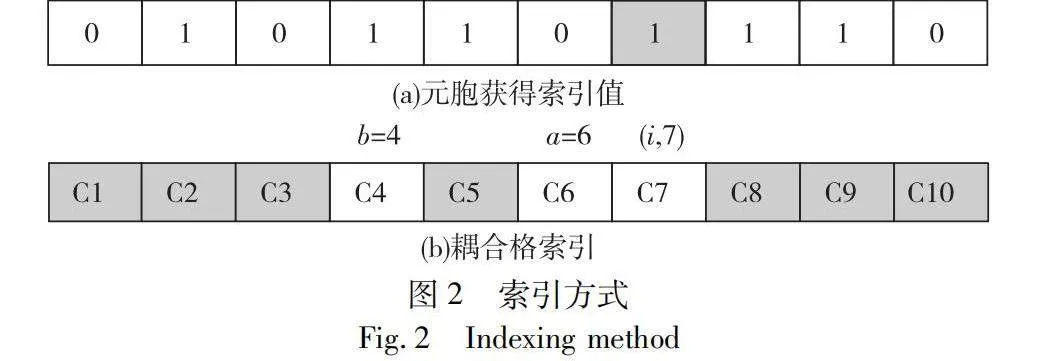
其中：i，j表示當前格子索引值；find（i， j）表示在TDECA中第i行、第j列上元胞狀態值分別為1的個數。以水平方向索引確定過程為例，豎直方向上的索引確定過程和此類似，相關步驟如下：TDECA第i行序列為0101101110，狀態值為1的元胞數量為6，在第7號位置，最終確定索引值為a=6和b=4，搜索過程如圖2所示。

由于各個格子所在行、列不完全相同，格子的索引值a、b、c、d不同，均在［1，L］動態變化，使得能量變化在系統中快速傳播，降低了格子的關聯性，提升了系統的安全性。

2.2 擾動值

擾動值p（S_n（i， j））是通過TDECA迭代過程中水平和豎直方向兩組狀態共同組合得到的，本文分別取TDECA系統迭代過程中第（i，j）個元胞所在行、列序列中間各32 bit進行異或運算最終組成共32位01序列對系統進行擾動，擾動值計算規則為

p（S_n（i， j））=bin2dec（XOR（S_n（i，34：65），S_n（34：65， j）））（13）

其中： bin2dec（）函數表示將二進制數轉換為十進制數;S_n是由元胞狀態組成的一個二進制數。

S_n（i，34：65）=b_（i，34）b_（i，35）b_（i，36）…b_（i，65）（14）

其中：b_（i，34）表示第i行、第34個元胞的狀態值。豎直方向的原理相同，由于TDECA中各個元胞是在不斷迭代變化的，所以擾動值的大小也是在不斷變化的，這使得擾動值的變化也是隨機的，能夠有效緩解系統的動力學退化現象^［21］。

2.3 擾動符號

擾動符號δ（S_n（i， j））是根據TDECA迭代結果來確定。

δ（S_n（i， j））=1 S_n（i， j）=1

－1 S_n（i， j）=0 （15）

其中：S_n（i， j）表示第n次迭代過程中，TDECA坐標（i，j）元胞的狀態。

由式（9）可知擾動符號的值為±1，并且不斷迭代，δ（S_n（i， j））的數值也不斷變化，所以每個格子的擾動值是不同的，降低了格子的相關性，提高了系統的復雜度。

3 混沌特性分析

2D-DPCML各項參數如下：控制參數μ（0lt;μ≤4），耦合系數ε（0lt;εlt;1），格子數量為10×10，logistic映射初值為0.05，而TDECA采用的兩種迭代規則為第105與150號。

為了與本文2D-DPCML系統進行對比，本文分析了傳統二維時空混沌系統（two-dimensional coupled map lattices，2D-CML）、基于 Arnold 映射的二維非線性耦合映像格（two-dimensional nonlinear coupled map lattices，2D-NLCML）系統^{［12，23］}、基于偽隨機耦合和PWLCM-Sin 映射的二維混合偽隨機耦合 PS 映像格（two-dimensional mixed pseudo-random coupling PS map lattice，2D-MCPML）系統^［15］。2D-NLCML 系統中，Arnold參數p=12、q=7，確保系統維持混沌特性。2D-MCPML 系統中，參數σ=0.5，其他參數設置和 2D-DPCML 保持一致。

3.1 回歸映射

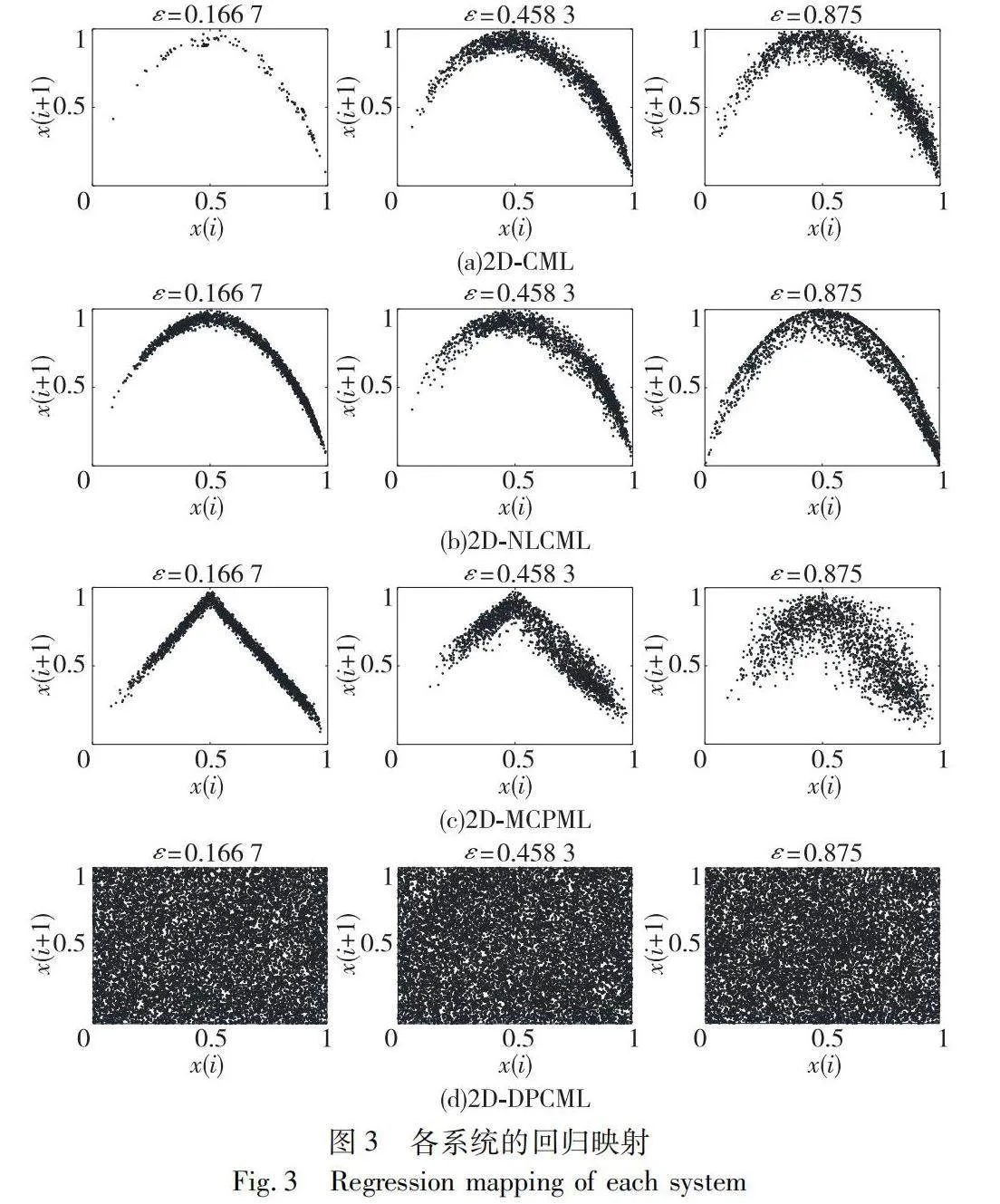
回歸映射衡量的是兩個相鄰格子間的狀態值的對應關系，混沌序列均勻分布時，回歸映射圖呈分散特性。回歸映射分析攻擊能估算系統的參數，可能破解混沌加密^［24］。點集中的回歸映射圖意味著較低安全性。本文分析了坐標（5，5），在控制參數3.99、耦合系數0.166 7、0.458 3、0.875下，迭代15 000次后的回歸映射如圖3所示。

圖3（a）～（c）顯示2D-CML和2D-NLCML系統的回歸映射點主要圍繞拋物線，2D-MCPML的點則靠近直線。耦合強度ε提升導致點分散。這反映了三系統對ε變化高度敏感，增加受回歸映射攻擊的風險。

與此相比，在圖3（d）展示的2D-DPCML系統中，回歸映射的分布呈現為雜亂無章的噪聲點，沒有形成任何明顯的聚集模式。即使在耦合強度ε發生變化時，其回歸映射分布依舊保持一種均勻散布的狀態，顯示出對耦合強度改變的高度魯棒性。因此，可以認為2D-DPCML系統在很大程度上能有效防御回歸映射分析攻擊，這為其在信息安全領域的應用提供了可靠的保障。

3.2 李雅普諾夫指數和K熵

Lyapunov指數是描述動力系統中混沌程度的重要指標之一。它表示了系統中微小初始條件的指數增長率，正的Lyapunov指數表明系統呈現混沌行為，而負的Lyapunov指數則意味著系統趨向于穩定。系統至少存在一個正的Lyapunov指數時，稱之為混沌系統^［25］，這意味著它對初始條件極其敏感，即使微小的變化也可能導致系統行為的巨大差異。而當系統具有多個正的Lyapunov指數時，則被稱為超混沌系統，這表明系統的混沌程度更加復雜，其軌跡的分離速度更快，對初始條件的敏感性更高。 Lyapunov指數的計算是混沌系統分析中的關鍵步驟，能夠幫助人們理解系統的動力學特性和混沌行為。

通過分析系統產生的序列計算Lyapunov指數（LE）之后，使用Kolmogorov-Sinai熵密度（KED）和Kolmogorov-Sinai熵闊度（KEB）指標來描繪系統的時空特征。其公式為

h=∑ni=1λ⁺（i）/L（16）

hu=L⁺/L（17）

其中：h代表KED；hu表示KEB。KED為系統中所有正Lyapunov指數的平均值，用于評價系統混沌度，其中i指系統空間維度；L是格子數；L⁺為正LE的格子數；λ⁺（i）表示正LE的總和。公式如下：

λ⁺（i）=λ（i）

λ（i）gt;00 λ（i）≤0 （18）

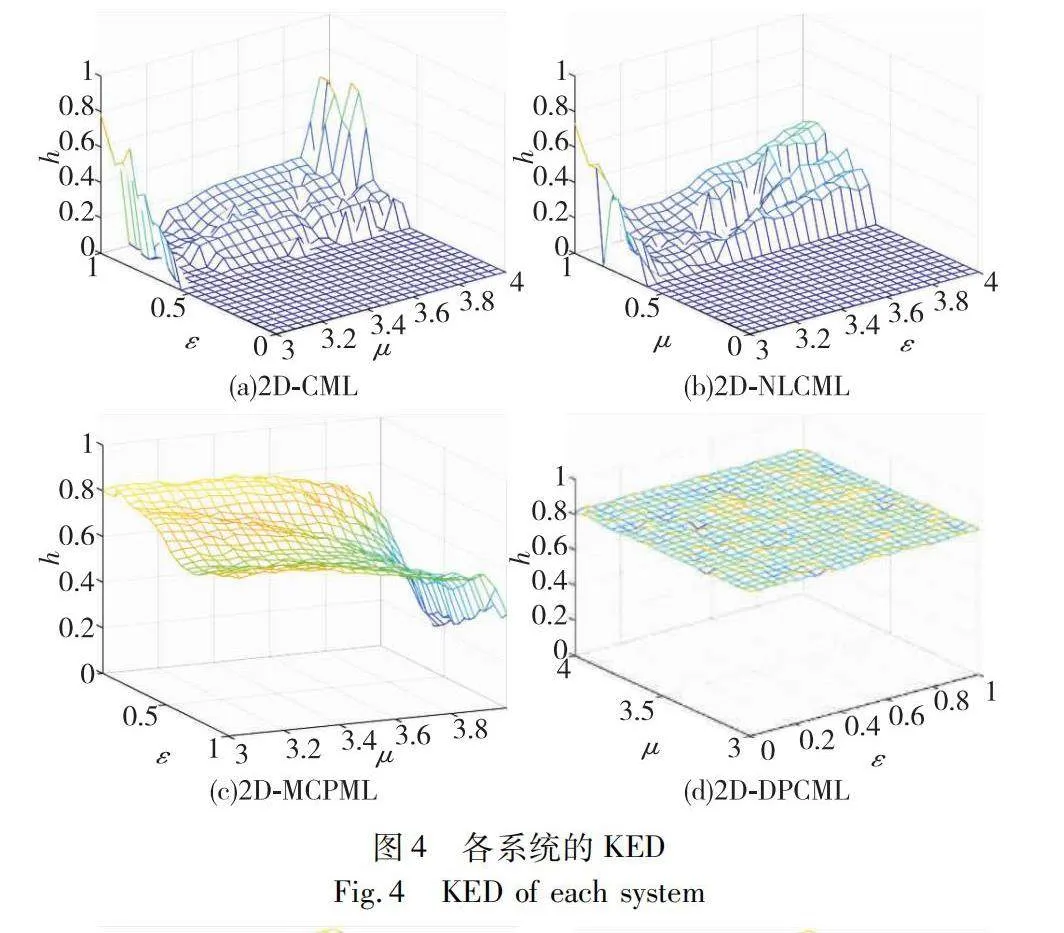
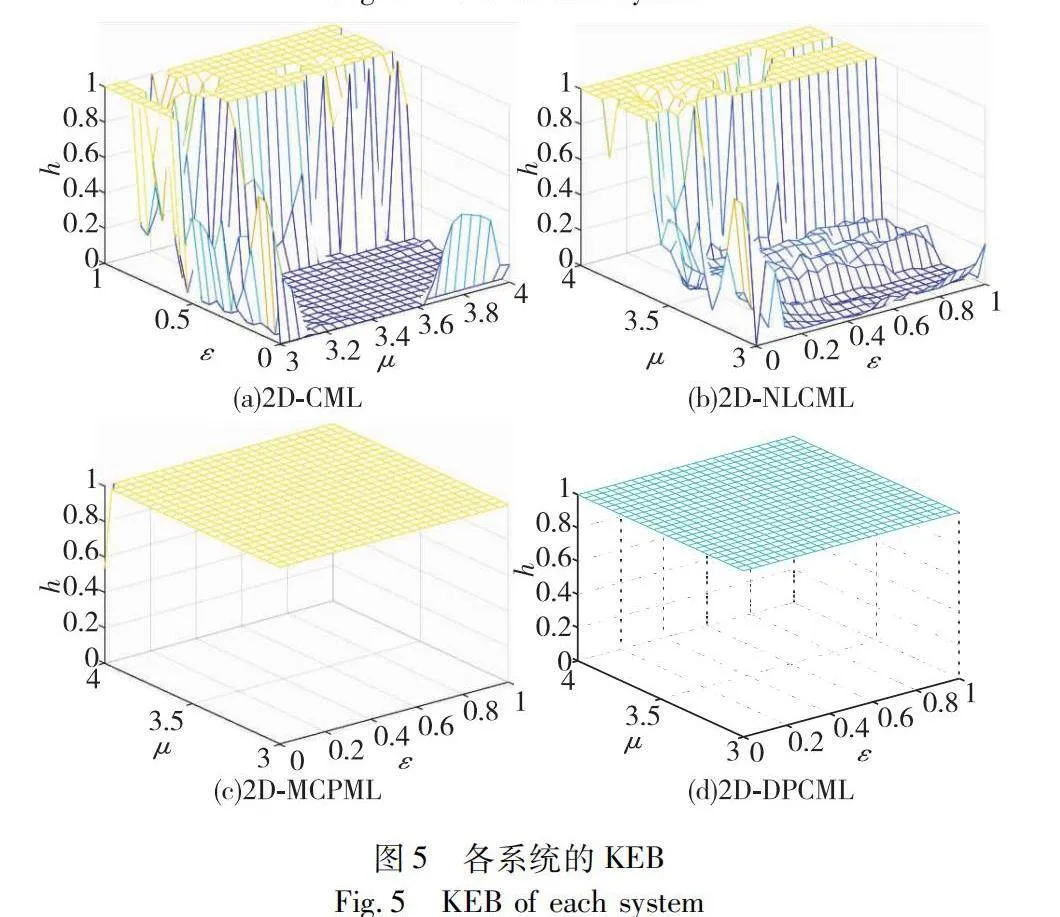
hgt;0時，系統進入混沌狀態。隨著h值增加，數值為1的hu數量上升，系統的混沌特性增強。不同參數下的h與hu值的變化展現于圖4、5。

當μgt;3.6時， 2D-CML與2D-NLCML才有正的KED值，在2D-CML系統中，當耦合強度ε約為0.2時，出現了一個較弱的混沌區間，此時僅有52.8%的格子的KED值大于0。相比之下，在2D-NLCML系統中，這個情況有所改進，且隨著ε值的升高，KED值也逐步增加。KED大于0的格子占總體的86.4%，但KED大于0.5的格子僅占1.12%。

在2D-MCPML與2D-DPCML中， KED均大于0，所有格子處于混沌。對圖4 （c）的深入分析，超過0.7的KED值的比例是32.64%。而在圖4（d）中，2D-DPCML的KED大于0.8的比例達到了99.68%，表明該系統的混沌特性明顯強于前三種系統。

因此，可以得出結論，2D-DPCML系統在混沌屬性上顯著超越了前三個系統。這種改進對于混沌系統在實際應用中的穩定性和可靠性具有重要意義。

在圖5（a）（b）的分析中， 2D-CML和2D-NLCML系統展現出KEB值等于1的情形僅在μ大于3.6的時候出現，即在μ的值處于（3.6， 4］，系統內的所有格子都有可能達到混沌狀態。在2D-CML系統里，達到KEB值為1的格子比例是30.56%，而在2D-NLCML系統中，這一比例為29.76%，說明這兩個系統實現所有格子進入混沌狀態的能力有限。

相比之下，2D-MCPML這一比例為99.84%，2D-DPCML則達到100%，這表明所有格子呈現強混沌狀態。這表明后兩種系統在空間上建立混沌狀態的能力較強，這對于混沌系統的穩定性和可靠性具有重要意義。

3.3 分叉圖

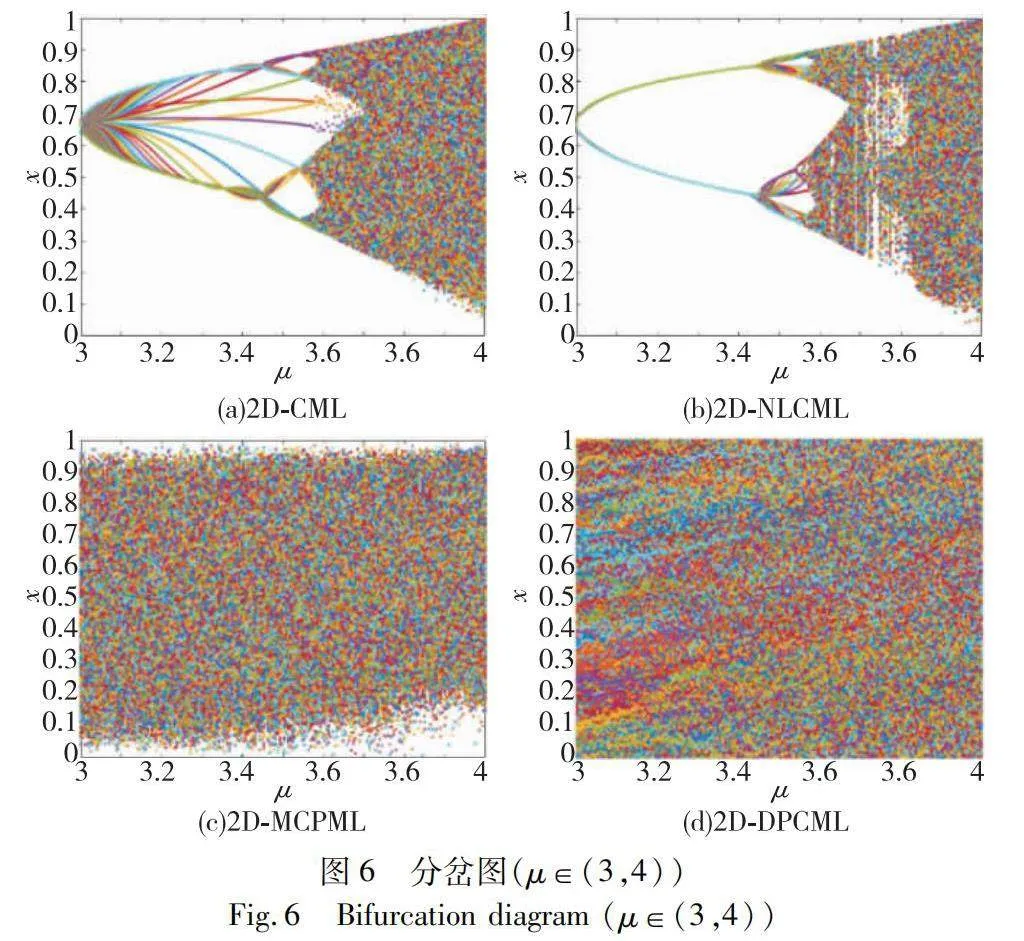
在對混沌系統的動力學性質進行深入分析時，分岔圖是一種非常有用的工具，該方法能夠生動描繪出混沌系統在不同參數設置下的遍歷行為。通過分析完整的分岔圖，能夠直接看到混沌系統何時達到混沌狀態、是否存在周期窗口。

如果混沌系統生成的序列在多次迭代之后能覆蓋整個區間，則表明該系統具有良好的遍歷性。在選定了特定的耦合系數ε之后，在給定初始化參數的控制下，對系統進行了2 000次迭代，并選擇了空間上位于位置（5，5）的格子進行對比分析。圖6清晰展示了在控制參數處于（3，4）時各個系統的分岔圖情況。

通過圖6（a）（b）可以發現，因為所有底層混沌映射均使用logistic映射，所以在分岔圖上可以清晰地看到周期性的點出現。尤其是當控制參數趨近于4的時候，系統展示出更加劇烈的混沌特征，這在整體上使得2D-CML的周期窗口比2D-NLCML更加突出，因此周期長度也更長。然而，在圖6（c）中卻沒有觀察到明顯的周期窗口。這表明在該控制參數范圍內，2D-MCPML系統具有較長的周期長度，但從遍歷性的角度來看，前三種系統都沒有完全覆蓋整個值域。

另一方面，在圖6 （d）中可以看到2D-DPCML系統在該區間內受控制參數的影響下，無論是周期長度還是遍歷性都得到了顯著的增強。在整個參數區間內，沒有觀察到任何周期窗口的存在，這意味著混沌序列的狀態值幾乎能夠填滿整個值域。因此，可以說2D-DPCML系統在該控制參數范圍內具有更加復雜的混沌軌跡和更好的遍歷性。

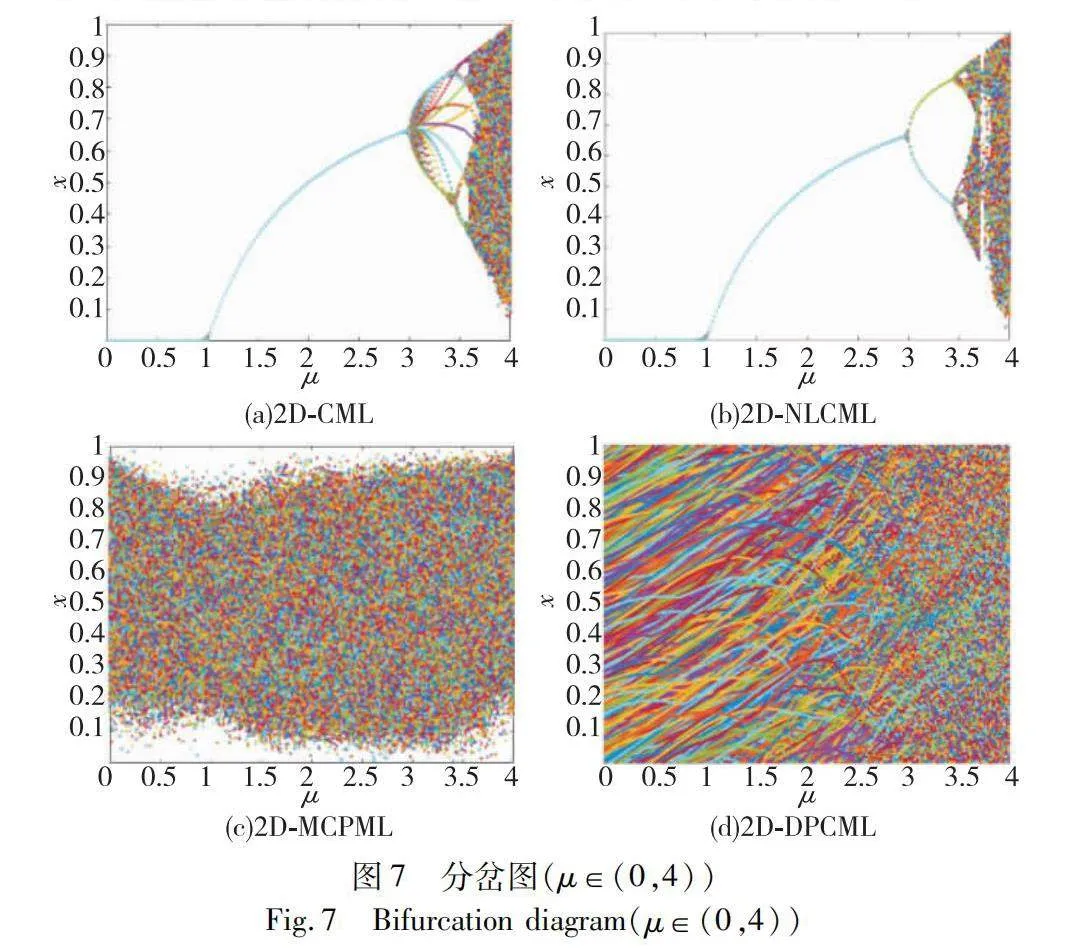
為更好地說明2D-DPCML，擴大了控制參數的選取范圍，圖7展示了各混沌系統控制參數在（0，4）上的分岔圖。

在這個特定的控制參數區間內，圖7（a）（b）中的2D-CML和2D-NLCML的分岔圖表現類似于logistic映射的性質。當觀察到圖7（c）時，2D-MCPML系統在混沌特性上與之前的兩種系統相似，在遍歷性方面略微減弱。在圖7（d）中，觀察到在（0，2）存在著類似平行軌道的現象，這表明在此區間內序列的復雜性仍然有待增強。然而，隨著控制參數的進一步增大，其混沌特性逐漸增強，并且混沌序列狀態值幾乎能夠填滿整個值域。這些發現表明在不同參數區間內，2D-DPCML系統展現出了豐富的動態行為，說明其對于控制參數要求不嚴格，在整個控制參數區間都能夠保持混沌狀態，且混沌值的分布較為均勻。

3.4 相關性分析

在將時空混沌系統融入加密體系時，保證生成的序列間相互獨立是至關重要的。這確保了即便攻擊者掌握了部分格子的序列數據，也不能推算出整個密鑰流，從而有效保護數據的安全性。因此，設計一個確保各個格子之間序列無關的耦合方案是至關重要的。這樣的方案將確保系統生成的密鑰流具有高度的隨機性和不可預測性，增強了密碼體制的安全性。

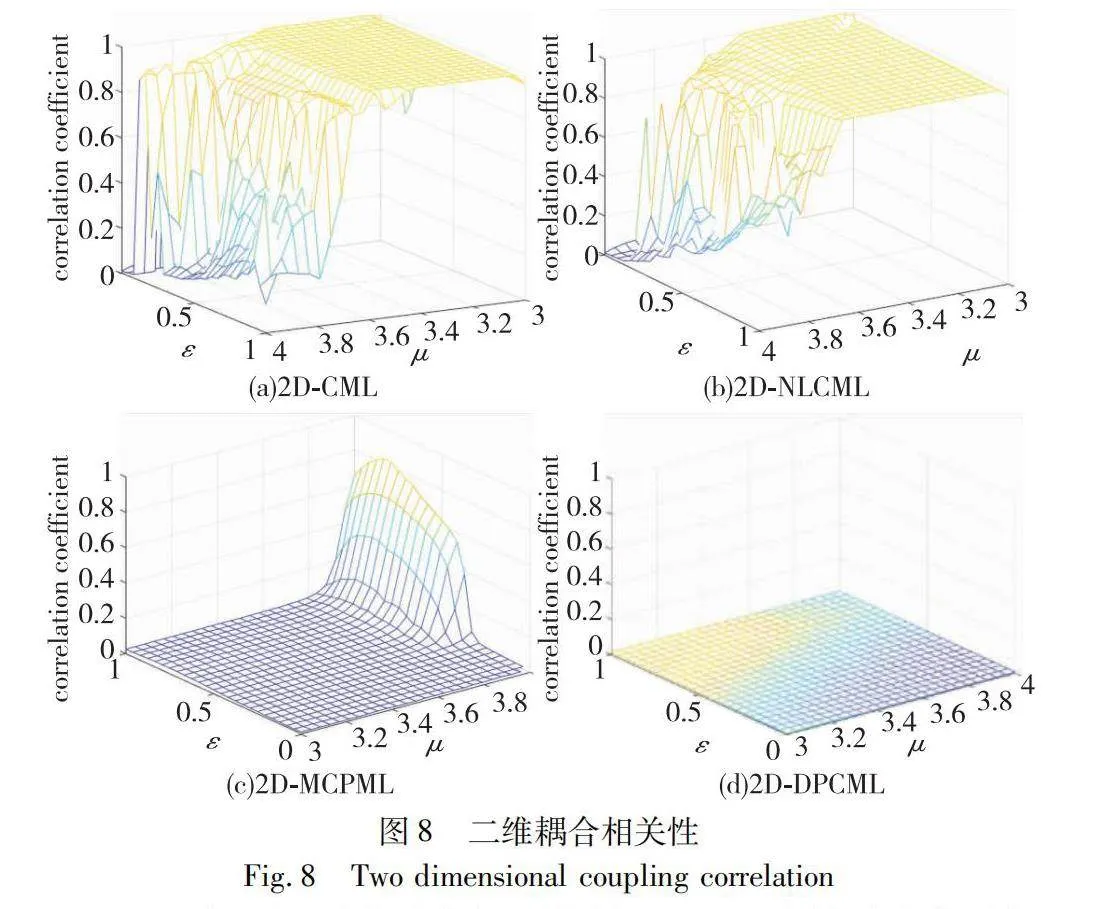
本文比較了2D-CML、2D-NLCML、2D-MCPML和2D-DPCML系統在不同設置的參數和耦合強度下，通過計算皮爾森相關系數的平均值來分析序列之間的相關性，具體結果展示在圖8中。

工程應用中，皮爾森相關系數低于0.3通常被認為序列間相互獨立。通過圖8的分析發現，在2D-CML與2D-NLCML系統里，只有11.36%和10.08%的參數對（μ， ε）導致序列間的相關性降至0.3以下。反觀2D-MCPML和2D-DPCML系統，這一比率分別提升至93.28%和100%，這一結果揭示了2D-DPCML生成序列間相關性極低，說明該系統安全性較高，適合應用于加密領域。

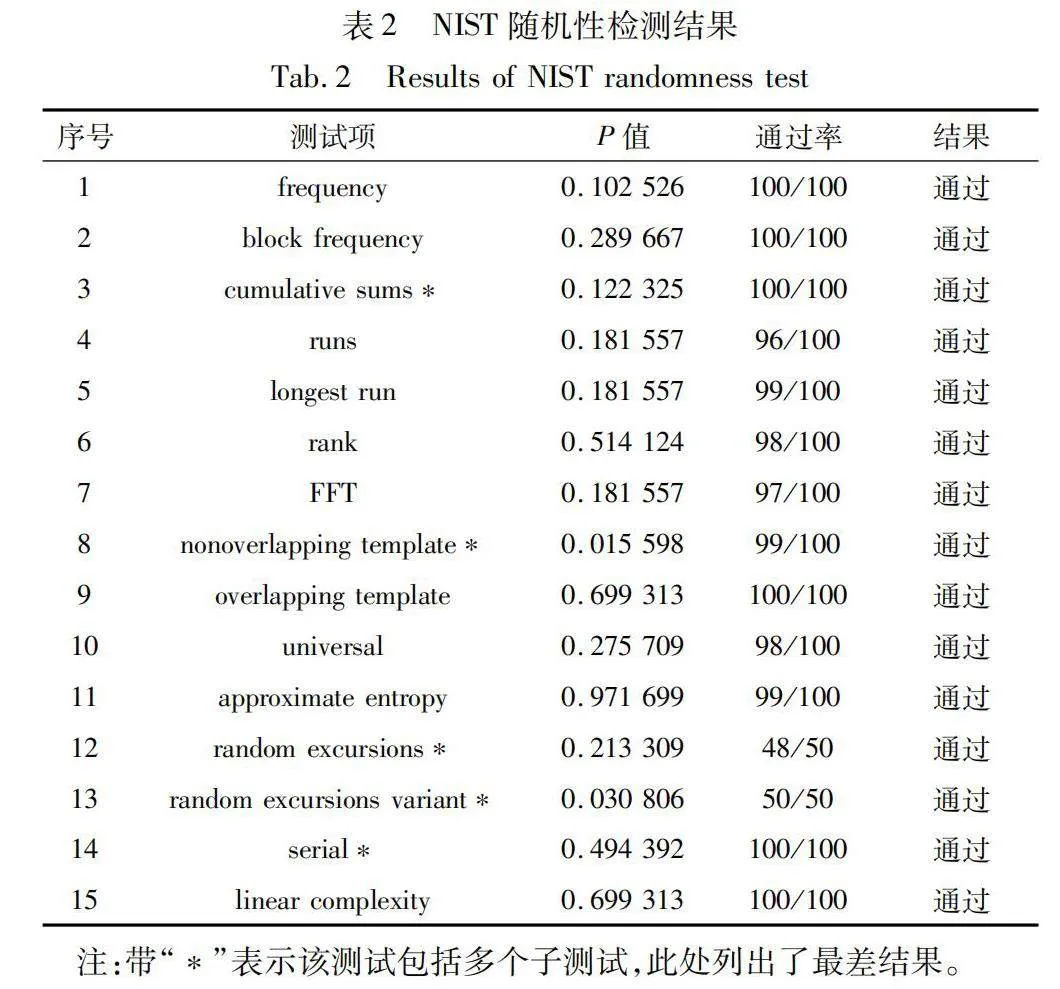
3.5 NIST隨機性檢測

NIST SP800-22測試套件旨在評定序列的隨機性及其不可預測性，成為廣泛應用的隨機性評估工具之一^［26］。該測試包括15種不同的子項，每項輸出一個值。在測試過程中，這個值將與閾值進行比較，若大于閾值，該序列則被認為通過了對應的子項測試。在本研究中，通過了測試標準的序列，其隨機性達到了99%的信度。本次測試采用了105和150號規則，在2D-DPCML經過10⁶次迭代，產生了一條長度達到100×10⁶的混沌序列，這條序列被分成100個組，每個組的序列長度同樣是100×10⁶，形成偽隨機二進制序列，測試結果詳見表2。

由表2可知，量化后的01序列通過了隨機性的測試，說明其滿足了加密算法對隨機序列的要求，為之后圖像的擴散和置亂奠定了應用基礎。

4 圖像加密算法

4.1 加密算法

2D-DPCML系統在非周期性和其他動力學特性上有著較好的表現，本文在此基礎上設計了一種圖像加密算法，流程如圖9所示。

假設輸入的明文圖像P大小為M×N，算法具體流程如下：

a）讀取一幅M×N原始灰度圖像I。將圖像I作為密鑰生成器的輸入，進行SHA-256運算得到256 bit二進制數，用來生成混沌系統各項初始化參數。

b）根據式（6），由步驟a）得到的256 bit二進制數對2D-DPCML進行初始化，具體初始化數據如下：

μ=3+3×key（33∶64）2³²－1ε=0.5×key（1∶32）2³²－1x=0.05（19）

其中：μ、ε、x分別表示2D-DPCML的控制參數、耦合強度和初值。

c）初始化完成后，迭代2D-DPCML，對混沌值進行處理，產生長度為M×N的混沌矩陣。

d）將量化后的矩陣與明文圖像按位進行異或。

e）再次對混沌值進行整理，生成大小為M+N的一條實值序列。首先選取前M個混沌實值，對M個混沌實值按照大小降序排序，同時得到排序后相較于排序前的索引號，并按照這個索引號對行進行亂序重排；列變換原理相同，選取后N個混沌實值進行大小降序排列，并得到排序后索引值，根據索引值對列進行重排。經過行方向和列方向上的重排，圖像像素值的位置被隨機進行了置亂，其行列變換如圖10所示。

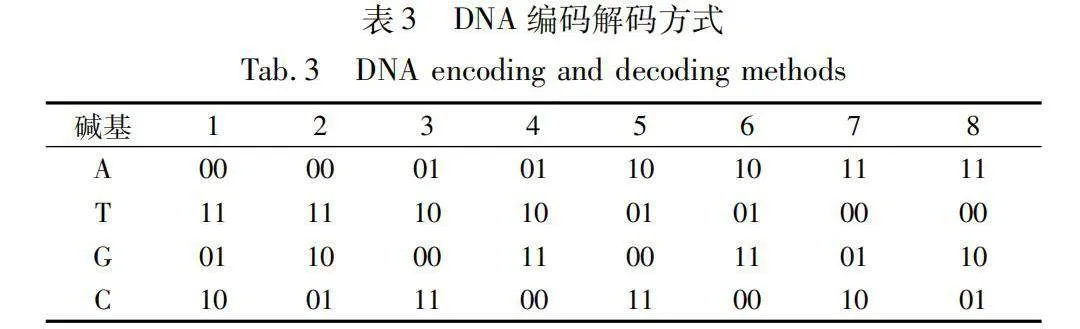
f）DNA編碼與運算。遺傳物質DNA由A、T、C、G四種堿基構成。其中A與T，C與G互補。同樣，通過將2 bit的01全排列的4種情況，即00、01、10、11來對應四種堿基，該過程并稱為DNA的編碼。由于要滿足互補規則，故總共有8種編碼規則，同樣，解碼也有8種規則，通過一輪編解碼，圖像的像素值對應的被成功替換，具體編解碼規則如表3所示。

對得到的像素矩陣以及重排后的混沌矩陣進行分塊的DNA編碼、DNA運算、DNA解碼。其中編碼、運算、解碼的規則由不同的子混沌矩陣控制。DNA運算包括加法、減法、同或和異或四種規則。

經過DNA編碼與運算后得到密文圖像。

4.2 解密算法

解密過程就是加密過程的逆運算，將密文圖像進行逆DNA編碼、運算、解碼，隨后進行逆行列變換，最后再與混沌矩陣進行異或即可得到明文圖像。

5 加密結果與分析

5.1 加解密效果

實驗選擇Lena大小為512×512的灰度圖像作為測試對象，其加解密效果如圖11所示。從圖11可以明顯看出，經過加密后從圖片上看已經無法明確辨認明文圖像內容顯示的信息，視覺加密效果良好，密文圖像中的像素值分布比較均勻，直觀上看就只是分布密集的黑白色點。

5.2 直方圖分析

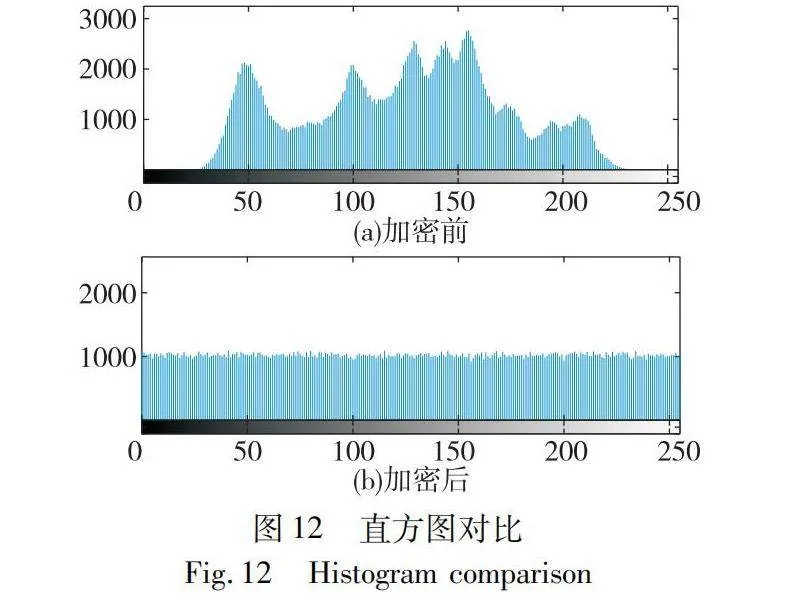
直方圖是對圖像中所有像素值的分布情況進行統計，將各像素值數量和對應的灰度級別用條形圖進行表示，每個條形圖高度表示該灰度級別下包含的像素數量。一個好的圖像加密算法，其密文圖像的像素值分布應該是均勻的，攻擊者不能通過對像素灰度值的分布進行統計分析而得出相關的圖像信息，加密前后的圖像像素直方圖如圖12所示。

從加密前后的直方圖對比可以看出，明文的像素分布較為集中，具有明顯的統計特性。而經過加密算法的加密后，密文的像素分布均勻，各灰度值的像素點數量大致一致，降低了圖像像素統計特性，增加圖像的安全性。

5.3 相鄰像素相關性分析

圖像作為多媒體傳輸的主要形式，其特點之一為相鄰像素相關性較高，信息冗余度大。相關性分析可以檢測出加密后的圖像是否仍然存在和明文圖像有關且較為明顯的統計規律和特征信息，避免攻擊者利用相關信息破解加密算法。本文抽取每個測試對象水平、垂直、對角方向上的5 000對像素點進行分析，相關性系數的計算公式如下：

C=∑ki=1x_i－1k∑ki=1x_iy_i－1k∑ki=1y_i∑ki=1x_i－1k∑ki=1x_i²×∑ki=1y_i－1k∑ki=1y_i²

（20）

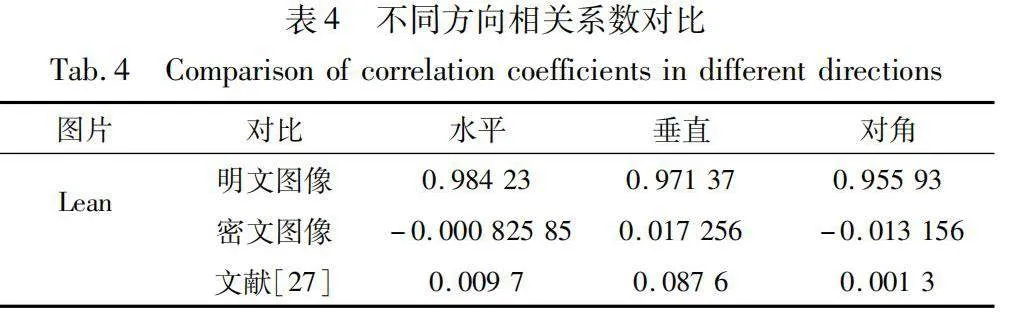
其中：x_i、y_i表示兩個不同方向上的像素值；k表示抽取的像素點對數，本節中k的值為5 000。加密前后測得的相關系數如表4所示，加密前后相鄰像素相關性對比如圖13所示。

通過表4和圖13可以得出，明文圖像中測得的相關系數更接近與1，相關性較強，在圖中明文圖像相鄰像素分布集中在對角線上；而經過加密以后的圖像相關系數更加接近于0，在圖中像素均勻分布在整個像素空間，因此加密后圖像的混亂程度更高。從表4對比可以看到本文提出的圖像加密算法顯著降低了明文圖像的相鄰像素相關性，比文獻［27］性能更優。

5.4 信息熵分析

圖像信息熵是衡量圖像加密后隨機性的一個重要指標，對于一個8 bit的灰度圖像，加密后所有灰度值出現的概率等概，此時的隨機性最大，信息熵也最大，理想值為8。信息熵的計算公式如下：

H（x）=－∑255i=0p（x_i）log₂p（x_i）（21）

其中：x_i表示像素值；p（x_i）表示該像素值出現的概率。

利用式（21）計算信息熵，得到的結果如表5所示。

從表5信息熵統計結果可以看出，本文設計的加密方案得到的信息熵接近理論期望值8，攻擊者難以通過該方案加密的圖像獲得有關明文信息。

6 結束語

在基于元胞自動機的基礎上，本文設計了一種二維動態元胞自動機新型系統，旨在提高系統的周期性和降低自相關性。為解決傳統混沌映射遍歷性差等問題，本文介紹了一種基于二維動態元胞自動機的偽隨機耦合映像格系統。系統通過分析TDECA的狀態值來選定耦合對象，并采用動態擾動對系統擾動調整，有效緩解混沌系統在有限精度數字計算機上的動力學退化現象。通過對比分析不同性能指標，發現所提方案生成的混沌序列更具隨機性，顯著優化了系統的周期性表現。此外，該方案的序列通過了NIST標準測試，證明了其具有較高的動力學復雜度，能夠在有限資源條件下生成更多偽隨機序列。

在此基礎上，設計實現了一種圖像加密算法，結合混沌系統和DNA編碼等相關模型和算法，對于加解密進行了直方圖等性能測試分析，發現其具有較好的加密性能。接下來將探索該系統在圖像加密及其他相關領域的應用潛力。

參考文獻：

［1］Flores-Vergara A， García-Guerrero E E， Inzunza-González E， et al. Implementing a chaotic cryptosystem in a 64-bit embedded system by using multiple-precision arithmetic［J］. Nonlinear Dynamics， 2019， 96（1）： 497-516.

［2］Chen Chen， Sun Kehui， He Shaobo. An improved image encryption algorithm with finite computing precision［J］. Signal Processing， 2020， 168： 107340-107340.

［3］Luo Yuling， Liu Yunqi， Liu Junxiu， et al. Counteracting dynamical degradation of a class of digital chaotic systems via unscented Kalman filter and perturbation［J］. Information Sciences， 2021， 556： 49-66.

［4］Kaneko K. Spatiotemporal intermittency in coupled map lattices［J］. Progress of Theoretical Physics， 1985， 74（5）： 1033-1044.

［5］Kaneko K. Chaos focus issue on coupled map lattices［J］. Chaos， 1992， 2： 279-408.

［6］Wang Xingyuan， Yang Jingjing， Guan Nana. High-sensitivity image encryption algorithm with random cross diffusion based on dynamically random coupled map lattice model［J］. Chaos， Solitons amp; Fractals： the Interdisciplinary Journal of Nonlinear Science， and Nonequilibrium and Complex Phenomena， 2021， 143： 110582.

［7］Zhang Yingqian， Wang Xingyuan， Liu Liyan， et al. Spatiotemporal chaos of fractional order logistic equation in nonlinear coupled lattices［J］. Communications in Nonlinear Science and Numerical Si-mulation， 2017， 52： 52-61.

［8］Dong Youheng， Zhao Geng. A spatiotemporal chaotic system based on pseudo-random coupled map lattices and elementary cellular automata［J］. Chaos， Solitons amp; Fractals， 2021， 151： 111217.

［9］Wang Mingxu， Wang Xingyuan， Zhao Tingting， et al. Spatiotemporal chaos in improved cross coupled map lattice and its application in a bit-level image encryption scheme［J］. Information Sciences， 2021， 544： 1-24.

［10］Peng Yuexi， Sun Kehui， He Shaobo. An improved return maps me-thod for parameter estimation of chaotic systems ［J］. International Journal of Bifurcation and Chaos， 2020， 30（4）： 2050058.

［11］Zhang Anguo， Xu Zheng. Chaotic time series prediction using phase space reconstruction based conceptor network［J］. Cognitive Neurodynamics， 2020， 14（6）： 849-857.

［12］Zhang Yingqian， He Yi， Li Pi， et al. A new color image encryption scheme based on 2DNLCML system and genetic operations［J］. Optics and Lasers in Engineering， 2020， 128： 106040.

［13］Zhang Yingqian， He Yi， Wang Xingyuan. Spatiotemporal chaos in mixed linear-nonlinear two-dimensional coupled logistic map lattice［J］. Physica A： Statistical Mechanics and its Applications， 2018， 490： 148-160.

［14］Wang Mingxu， Wang Xingyuan， Wang Chunpeng， et al. Spatiotemporal chaos in cross coupled map lattice with dynamic coupling coefficient and its application in bit-level color image encryption［J］. Chaos， Solitons and Fractals： the Interdisciplinary Journal of Nonlinear Science， and Nonequilibrium and Complex Pheno-mena， 2020， 139： 110028.

［15］Zhou Peizhao， Du Junxiao， Zhou Kai， et al. 2D mixed pseudo-random coupling PS map lattice and its application in S-box generation［J］. Nonlinear Dynamics， 2021， 103（1）： 1-16.

［16］Neumann J， Burks A W. Theory of self-reproducing automata［M］. Urbana： University of Illinois Press， 1966.

［17］宮姍. 一種基于混合細胞自動機的加密算法研究［D］. 長春： 東北師范大學， 2016. （Gong Shan. Research on an encryption algorithm based on hybrid cellular automata［D］. Changchun： Northeast Normal University， 2016.）

［18］Ning Hao， Zhao Geng， Dong Youheng， et al. Spatiotemporal chaos in two-dimensional dynamic coupled map lattices system based on elementary cellular automata［J］. Nonlinear Dynamics， 2022， 109（3）： 2143-2161.

［19］羅慧軍. 基于混沌元胞自動機的圖像加密算法的研究與實現［D］. 贛州： 江西理工大學， 2011. （Luo Huijun. Research and implementation of image encryption algorithm based on chaotic cellular automata［D］. Ganzhou： Jiangxi University of Science and Tech-nology， 2011.）

［20］Kaneko K. Pattern dynamics in spatiotemporal chaos： pattern selection， diffusion of defect and pattern competition intermettency［J］. Physica D Nonlinear Phenomena， 1989， 34（1-2）： 1-41.

［21］Li Shujun， Chen Guanrong， Mou Xuanqin. On the dynamical degradation of digital piecewise linear chaotic maps［J］. International Journal of Bifurcation and Chaos， 2005， 15（10）： 3119-3151.

［22］趙耿， 潘周， 馬英杰， 等. 新型一維偏移耦合映像格系統及其動態特性［J］. 計算機應用研究， 2023， 40（11）： 3289-3293， 3302. （Zhao Geng， Pan Zhou， Ma Yingjie， et al. Novel one-dimensional migration-coupled mapping lattice system and its dynamic characteristics［J］. Application Research of Computers， 2023， 40（11）： 3289-3293， 3302.）

［23］He Yi， Zhang Yingqian， Wang Xingyuan. A new image encryption algorithm based on two-dimensional spatiotemporal chaotic system［J］. Neural Computing and Applications， 2020， 32（1）： 247-260.

［24］Yan Dongxue， Fu Xianlong. Asymptotic analysis of an age-structured HIV infection model with logistic target-cell growth and two infecting routes［J］. International Journal of Bifurcation and Chaos， 2020， 30（4）： 2050059.

［25］劉兆龍. 基于混沌的流密碼算法研究［D］. 重慶： 重慶郵電大學， 2016. （Liu Zhaolong. Research on chaos-based stream cipher algorithm ［D］. Chongqing： Chongqing University of Posts and Telecommunications， 2016.）

［26］王永， 馬鍵濱， 陳燕， 等. 一種新的基于時空混沌的偽隨機數發生器［J］. 計算機工程與應用， 2018， 54（11）： 97-102. （Wang Yong， Ma Jingbin， Chen Yan， et al. New pseudo-random number generator based on spatiotemporal chaos［J］. Computer Engineering and Applications， 2018， 54（11）： 97-102.）

［27］Wang Xinyuan， Guan Nana. A novel chaotic image encryption algorithm based on extended Zigzag confusion and RNA operation［J］. Optics amp; Laser Technology， 2020， 131： 106366.