基于樹結構貝葉斯優化的隧道三維地應力智能反演方法

摘要：為了合理地獲取長大深埋隧道的地應力場分布特征，文章以數值模擬與機器學習作為主要工具，從數值模擬邊界條件科學構造與集成學習GBDT算法模型的構建與優化兩方面入手，建立基于TPE-GBDT的隧道三維地應力反演方法，并以昌寧隧道作為應用案例開展三維地應力智能反演。反演結果與地應力實測結果相比誤差在10%以內，說明了該方法的可靠性。

關鍵詞：TPE；GBDT；隧道；地應力；智能反演

中圖分類號：U456.2" " " 文獻標識碼：A" " "DOI：10.13282/j.cnki.wccst.2024.11.041

文章編號：1673-4874（2024）11-0136-05

0引言

地應力反演的常用方法有多元線性回歸反演與非線性反演方法。多元線性回歸分析法采用最小二乘法求解回歸系數且解唯一，故被廣泛采用［1］。但是，該方法因其線性假設忽略了影響初始地應力各因素之間的相互作用，且實際情況的初始地應力與影響初始地應力的各因素之間的關系難以用線性函數表達［2］。非線性反演方法在求解非線性復雜問題時具有較為突出的優勢。得益于當前人工智能技術的發展，已有大量的學者基于各類智能算法進行地應力反演研究［3-4］。但當前在采用智能算法進行地應力反演研究中仍存在著一些需要改進的問題：（1）在建立數值模型時，對于邊界條件的取值范圍極少有研究指明其出處，根據判斷大多靠人工試算得到，這無法形成科學方法供參考應用；（2）集成學習已經成為當前機器學習方面的熱點，其具備對連續、離散數據同樣強大的處理能力，但卻較少在地應力反演研究中應用。

因此，本文以數值模擬與機器學習作為主要工具，提出一種基于樹結構貝葉斯優化梯度提升樹算法（TPE-GBDT）的隧道三維地應力智能反演方法。從數值模擬邊界條件科學構造與集成學習GBDT算法模型的構建與優化兩方面入手，建立基于TPE-GBDT的隧道三維地應力反演方法，并以實際工程為案例說明了反演結果的可靠性，為地應力反演研究提供參考。

1地應力場智能反演方法

1.1梯度提升決策樹（GBDT）算法

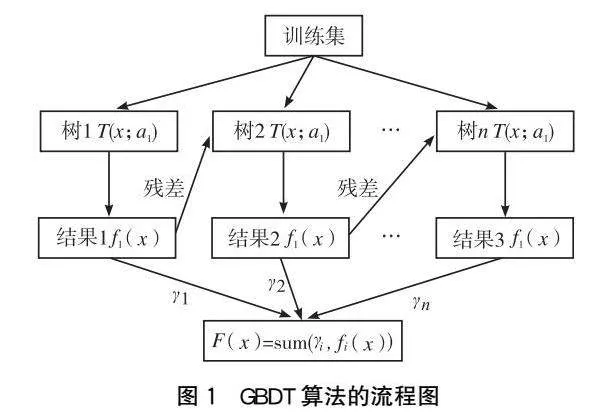
GBDT是一種以多棵決策樹作為基學習器的機器學習集成算法，采用了多模型集成的策略，針對殘差進行擬合，進而降低模型的偏差和方差。GBDT算法的流程如圖1所示。可以看出，前面的決策樹的殘差被作為下一個決策樹的輸入。新增的決策樹用于減少殘差，使損失函數在每次迭代中沿著負梯度方向減小。最終預測結果是基于所有決策樹結果的累加求和確定的［5］。相較于最小二乘回歸分析方法，GBDT算法能夠更好地解決自然界中低維數據的預測問題［6］。

1.2基于樹結構的貝葉斯優化算法

TPE（Tree-structured Parzen Estimator）是一種基于樹結構的貝葉斯優化算法。在TPE算法中，將貝葉斯優化框架中的概率代理模型設置為樹結構概率密度估計，利用損失函數將樣本分成高低兩個部分建立概率分布，同時將預期改進函數（Expected Improvement，EI）作為采集函，EI通過最大化目標函數未知區域和已知最優值之間的差異來選擇下一個參數組合，實現parameters空間的優化。通過最大化EI函數選擇參數組合，等同于最大化參數組合在概率分布中的最小概率與最大概率，從而自動尋找到能得到極大預期改進值的最優參數組合。

1.3基于TPE-GBDT的地應力智能反演過程

根據上述GBDT與TPE算法的基本原理與思路，本文建立了一種基于TPE-GBDT算法的隧道三維地應力智能反演方法，其實現流程如圖2所示，具體操作步驟如下：

（1）三維地質建模。基于勘查設計文件建立隧址區三維地質模型，用于地應力反演計算。

（2）邊界條件設置。根據自重及構造應力特征確定合理的邊界條件設置方式，并以地應力實測數據為基礎確定各邊界條件的取值范圍。

（3）樣本數據構造。將各邊界條件進行正交組合并帶入FLAC 3D軟件運行計算，提取計算結果，建立邊界參數-測點應力樣本數據。

（4）模型訓練與優化。將樣本數據帶入GBDT算法模型進行訓練，經GBDT決策樹殘差優化，獲得損失函數最小的邊界參數-測點應力映射關系，在此基礎上采用TPE算法，在GBDT參數空間自動尋找最優參數組合，對GBDT算法進行優化。

（5）模型驗證。將實測點地應力值帶入訓練好的TPE-GBDT模型求解，輸出得到對應邊界條件，對此邊界條件進行數值模擬正分析計算，得到三維模型任意一點地應力值，提取與實測點對應位置的地應力值與實測值對比，結果吻合證明模型性能良好，結果不吻合則返回步驟（4）。

（6）三維地應力反演。對模型輸出邊界條件進行正分析計算，即獲得隧道三維地應力場特征。

2工程應用

2.1工程概況

昌寧隧道位于云南省保山市昌寧縣境內，隧道全長5 km，屬特長隧道。隧址區地形起伏較大，最大埋深456 m，埋深＞300 m的區段占隧道總長的40.5%。地層巖性主要以中風化灰巖與中風化變質砂巖為主。在隧道開挖至K32+654段時，塌方、大變形等地質災害逐步顯現。根據現場經驗初步判斷其原因為高地應力所致，但由于尚不明確隧道沿線的地應力分布特征，無法根據隧道沿線地應力的變化提前制定合理的開挖支護方法。

2.2樣本數據構建

2.2.1數值模型

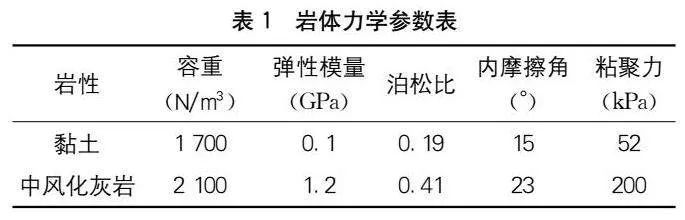
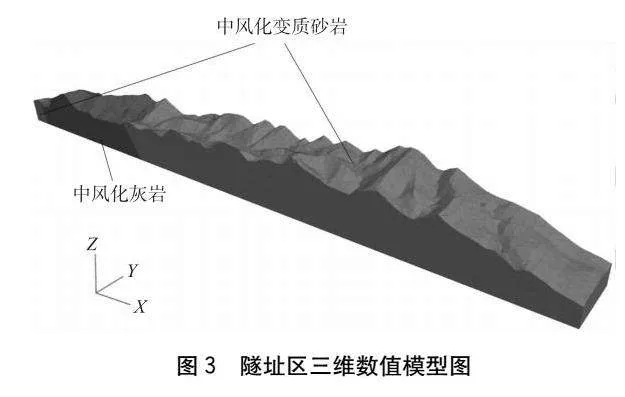
采用FLAC 3D軟件建立隧址區三維數值模型，模型以隧道走向為X軸，以與走向垂直方向為Y軸。為減小數值分析計算過程中邊界效應的影響，將計算范圍適當擴大，模型沿X軸與Y軸長度范圍分別為437 m和5 247 m，隧道主要穿越中風化灰巖與中風化變質砂巖地層，三維數值模型如圖3所示。各地層巖體力學參數參照地勘報告選取，如表1所示。

2.2.2邊界條件設置

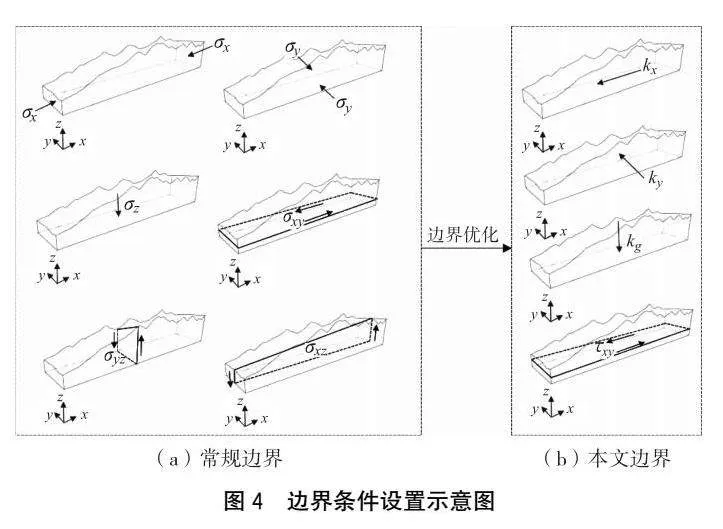
自重應力與構造應力的共同作用是造就當前地應力狀態的主要因素［7］。當前針對地應力反演的研究在設置邊界條件時，一般通過施加豎直向下的重力加速度來模擬自重應力，通過施加沿x、y方向的水平應力（位移）模擬水平向構造運動，通過施加xOy、yOz、xOz面上的剪切應力模擬剪切構造運動。這種方法看似合理，但其在地應力反演中應用時需要大量的試算以得到各個應力邊界相對合適的取值范圍，而試算過程中控制條件（邊界條件）多，導致很難得到各個邊界的合理取值范圍。

鑒于此，本文采用重力修正系數kg與側壓力系數kx、ky作為邊界條件，[JP3]通過調節側其值的大小來模擬自重與水平應力狀態，并施加xOy平面上的剪切應力τxy模擬剪應力狀態。由于隧道長度往往遠大于其寬度與埋深，因此忽略xOz、yOz平面的剪切運動，如下頁圖4所示。

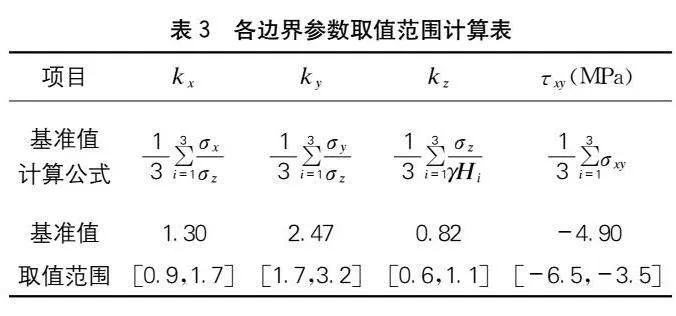
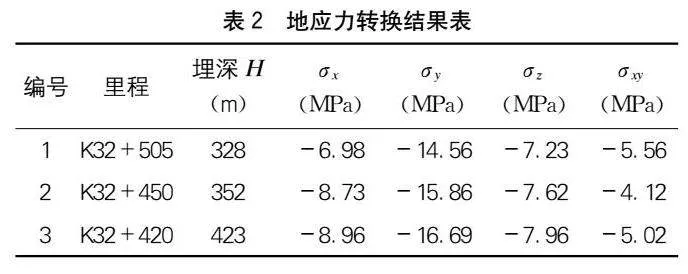
為科學、合理地確定4個邊界參數kg、kx、ky與τxy的取值范圍，首先根據隧道現場3個測點的地應力實測結果與三維數值模型坐標方向進行應力轉化，[JP3]如下頁表2所示。將表2中4個邊界參數的平均值作為基準值，將基準值的30%作為浮動范圍，進而確定各參數取值范圍的上下邊界。其具體計算方法與計算結果如下頁表3所示。

2.2.3樣本構造

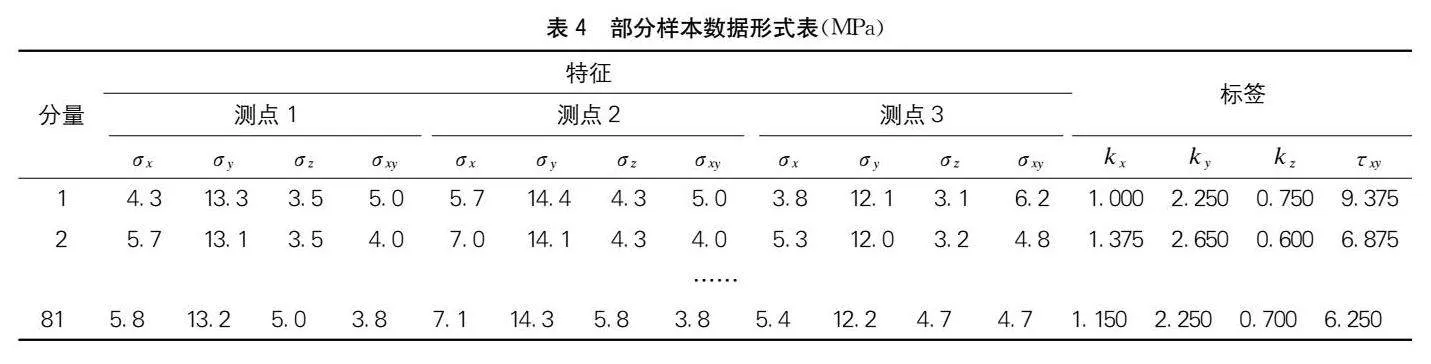
將邊界條件參數kx、ky、kz與τxy按照L81（94）采用4因素9水平正交試驗生成81組參數組合，分別提取每組的參數值代入FLAC 3D軟件中運行計算，計算結束后提取與實測點對應測點的應力值（σx、σy、σz、σxy），將參數組合與測點應力值一起組成樣本數據，如表4所示。

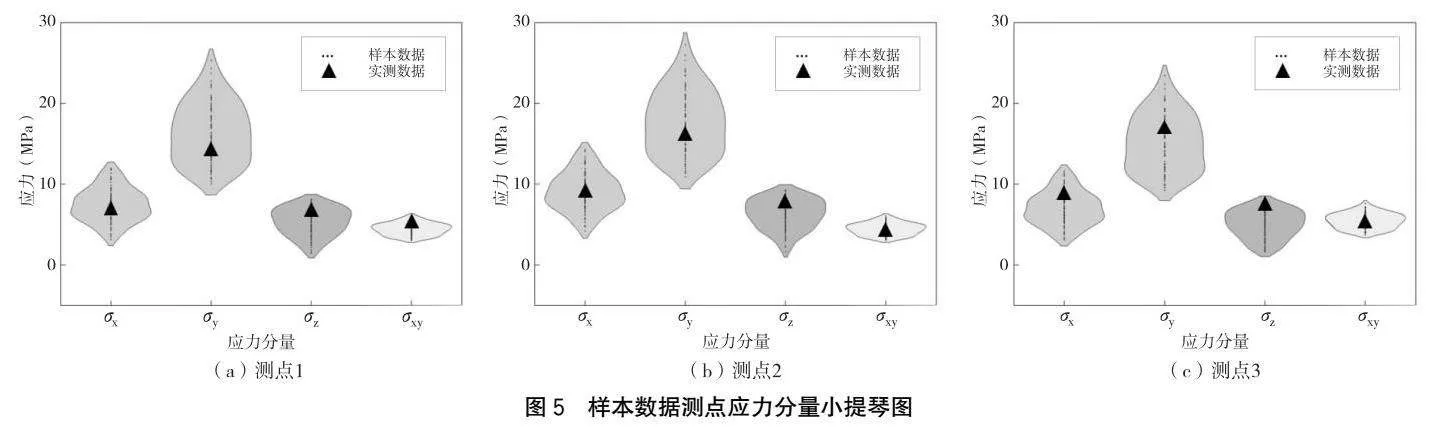
良好的樣本數據應該與實測數據保持較好的一致性。將81個樣本中3個測點的應力分量分別繪制為小提琴圖，如圖5所示。可以看出，樣本數據中各測點應力分量的取值范圍能夠全部包含實測值，其范圍略大于實測值范圍且越靠近邊界處分布數量越少，能夠較好地描述實測數據特征。

2.3模型訓練與優化

將樣本數據的80%（64組）劃分為訓練集，20%（17組）劃分為驗證集，分別對模型進行訓練與驗證。根據模型在驗證集上的預測結果分別計算其MAE、MSE、R2評價指標，如表5所示。

由表5可知，模型性能表現相對良好。但為了進一步提升模型的預測性能，采用TPE算法對GBDT模型超參數進行優化，其優化過程如下：

（1）定義目標函數。將GBDT模型的K折交叉驗證的最終分數作為目標函數，K取8。

（2）確定參數空間。初始參數空間為GBDT模型全部參數，在優化過程中逐步調整參數空間。

（3）定義優化函數并訓練貝葉斯優化器。采用TPE算法作為優化函數建立代理模型，輸入迭代次數自動訓練貝葉斯優化器并輸出超參數最優組合。由于超參數優化具有隨機性，因此需采用n次同樣迭代次數的訓練以保證結果的穩定性。

（4）對比n次迭代結果中各超參數的最優值，逐步剔除待優化參數或調整參數優化范圍。本文取n=3。

（5）重復步驟（2）～（4），直至得到參數空間中所有參數的最優組合。

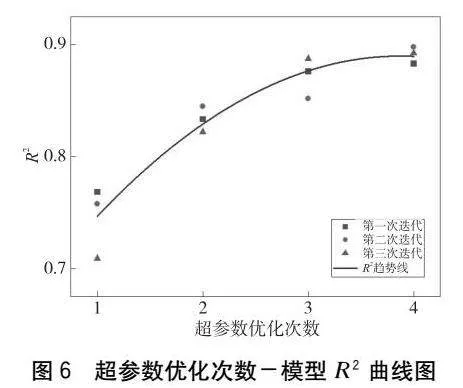
根據上述超參數優化過程，最終優化結果如表6所示。為了確定參數優化結果的可靠性，分別測試每次優化過程中得到的3個優化模型在測試集上的性能，共進行4次優化，將模型預測結果的R2及每次優化3個結果的平均值繪制于圖6。可以看出，經過4次優化后，模型的R2由0.85提升至0.89，且已基本趨于穩定，達到了模型的最佳性能。

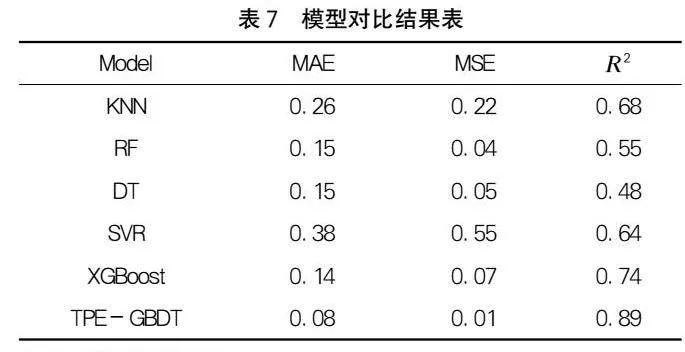
為了驗證以上建立的TPE-GBDT模型性能的優越性，采用同樣的訓練集與驗證集數據對常用的多輸出回歸模型進行訓練并驗證其性能，結果如表7所示。可以看出，本文建立的TPE-GBDT模型的MAE、MSE、R2指標均顯著優于其他型，說明了本文建立的地應力智能反演模型的可靠性。

2.4模型驗證

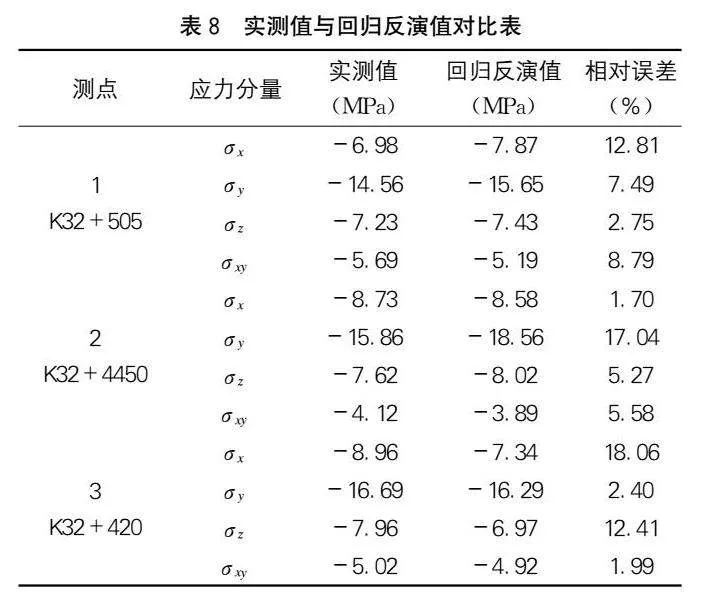
基于以上建立的TPE-GBDT模型，將實測地應力分量值（表2）作為輸入，輸出得到三維數值模型邊界參數，參數kx、ky、kz、τxy的反演輸出值分別為1.04、2.22、0.91、5.22，將此邊界參數代入數值模型運行計算，提取3個測點的地應力分量計算結果，如表8所示。

根據表8，基于TPE-GBDT算法的地應力反演結果，對各應力分量的預測最大相對誤差＜20%，對3個測點的12個應力分量預測的綜合誤差為8.02%，此誤差在地應力反演相關研究中相對較小，預測結果能夠滿足工程需求。這說明，利用本文建立的TPE-GBDT模型能夠較為準確地反演得到昌寧隧道三維地應力場，通過實際工程驗證了模型的有效性。

2.5地應力反演分析

將采用TPE-GBDT地應力反演模型預測得到的邊界條件參數代入數值模型運行計算，得到的結果即為昌寧隧道三維地應力場。提取隧道軸線處地應力場計算結果，如下頁圖7所示，整個隧道沿線中，K32+320～K32+680里程段落地應力值整體較高，存在高地應力災害風險。在后續隧道施工至該段落時，隧道拱頂坍塌、初期支護開裂、拱架扭曲變形等工程災害持續發生，如下頁圖8所示，這也從施工響應方面再次印證了昌寧隧道地應力反演結果的準確性。

3結語

為進一步提高隧道三維地應力反演的準確性，本文提出了一種基于TPE-GBDT的三維地應力智能反演方法，并說明了該方法的具體思路與實現流程。以此方法為基礎，結合地應力反演邊界條件優化，有效反演得到了昌寧隧道的三維地應力特征。經實測數據驗證與開挖過程施工響應對比，地應力反演結果能夠準確地體現昌寧隧道的三維地應力特征，說明了本文方法在隧道工程三維地應力反演中應用的可靠性。

參考文獻：

［1］郭懷志，馬啟超，薛璽成，等.巖體初始應力場的分析方法［J］.巖土工程學報，1983（3）：64-75.

［2］孫港，王軍祥，郭連軍，等.基于IA-BP智能算法的初始地應力場反演研究［J］.土木與環境工程學報（中英文），2023，45（2）：89-99.

［3］王慶武，巨能攀，杜玲麗，等.拉林鐵路桑日至加查段三維地應力場反演分析［J］.巖土力學，2018，39（4）：1 450-1 462.

［4］楊志強，高謙，翟淑花，等.復雜工程地質體地應力場智能反演［J］.哈爾濱工業大學學報，2016，48（4）：154-160.

［5］Liang，W.，Luo，S.，Zhao，G.，et al.Predicting Hard Rock Pillar Stability Using GBDT，XGBoost，and LightGBM Algorithms［J］.Mathematics，2020（8）：765.

［6］張晨，沈波，劉桂衛.浩吉鐵路某長深隧道地應力三維反演技術研究［J］.鐵道工程學報，2022，39（8）：30-34.

［7］張社榮，胡安奎，王超，等.基于SLR-ANN的地應力場三維智能反演方法研究［J］.巖土力學，2017，38（9）：2 737-2 745.

作者簡介：張坤牧（1983—），高級工程師，主要從事公路工程施工管理工作。

收稿日期：2024-05-16