汽車盲區問題

在綜合與實踐課堂中,同學們將面對現實生活中的具體背景,學會從數學的角度去發現問題,提出問題。這不僅要求我們會運用數學知識,有時還需要會整合其他學科的知識和方法,以全面分析和解決問題。“汽車盲區問題”便是生活中常見的問題,該問題包含以下幾個任務:
(1)盲區是如何形成的?其主要類型有哪些?
(2)如何估算汽車主要盲區面積的大小?
(3)有哪些手段可以減小駕駛員的盲區,保證駕駛過程中的安全性?
活動一:數學抽象
以小型轎車為例,轎車在靜止狀態時,其盲區主要分為車頭盲區、車尾盲區、后視鏡盲區、“A、B柱”盲區。在本活動中,我們主要來測量車頭盲區(記為盲區①)與車尾盲區(記為盲區②)兩個主要盲區的面積。
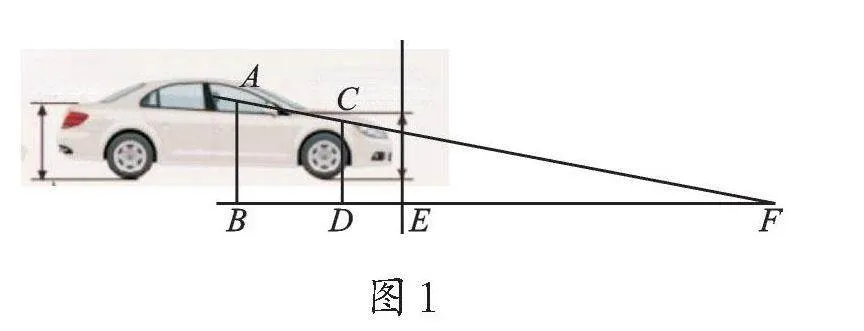
我們在小學階段學習了“觀察物體”,其中俯視圖(從上面向下看)能夠幫助大家確定兩種主要盲區在地面上的“位置”。從俯視圖看,需要測量或計算以下數據:盲區①和盲區②的長度與寬度,其中寬度即為轎車的車寬,而盲區的長度無法通過俯視圖計算。因此,我們需要調整策略,通過右視圖(從右面向左看)進行測量與估算,將某轎車右視圖抽象如下(如圖1)。
從右視圖來看,盲區①的長度即為EF的長度,則盲區①的面積=車寬×EF。
活動二:數學運算
結合圖1的分析,我們可以通過[ABBF]=[CDDF]這一關系計算EF的長度,將該式變形為[ABBE+EF]=[CDDE+EF]。因此,求解EF的長度,還需測量AB(人的視線高度)、CD(車前蓋最高處與地面高度,該距離大致等于車門高度)、BE(駕駛員與車頭距離)以及DE(車前蓋最高處與車頭的距離)。
活動三:類比探究
如圖2,我們可以通過[ABGH]=[BIHI]這一關系計算HI的長度,該式可變形為[ABGH]=[BH+HIHI]。因此,求解HI的長度,還需測量AB(人的視線高度)、GH(后備廂高度)、BH(駕駛員與車尾的距離)。
綜合以上內容,我們可以設計表1,記錄需要測量的數據。
通過活動二、活動三的計算公式,即可求得兩個主要盲區的面積。
活動四:實際運用
通過對以上數據的收集、整理與計算,我們可以思考如何解決以下實際問題。
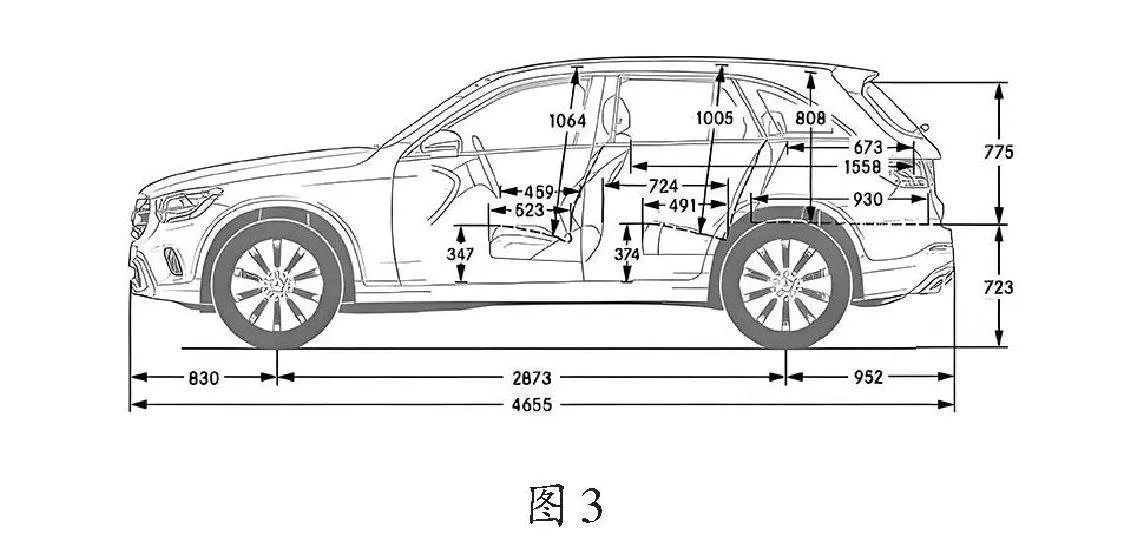
問題1:為何SUV車型與普通轎車相比,盲區較大?圖3為某SUV車型的左視圖(從左面向右看),結合以上過程進行說明。
問題2:對普通轎車而言,如何減小駕駛員的車前、車后盲區?
問題3:某車車身長度約為460cm,寬度約為190cm,車門高度約為109cm,后擋風玻璃高度約為110cm。駕駛員以最高坐姿即1.6m計算時,則車尾盲區的面積大約為多少?
資源拓展
我們剛才已經經歷了車頭盲區和車尾盲區的探究過程,下面思考如何研究其他不同類型的盲區(如后視鏡盲區、“A、B柱”盲區)面積,需要測量哪些數據。請查閱相關資料進行研究。
后視鏡盲區:車外后視鏡盲區,行駛過程中對該盲區未及時觀察,易發生碰撞,其面積需要基于9個檢測點處的曲率半徑與后視鏡曲率半徑進行研究。
“A、B柱”盲區:“A柱”是擋風玻璃兩側的柱子,“B柱”是前后車門之間的柱子,其面積需要在眼橢圓模型下測量兩個盲區障礙角度的數據。
在汽車行駛的過程中,還會存在內輪差盲區、超車盲區、山路盲區以及光線盲區等。我們可以查閱相關資料,了解不同盲區產生的原因,提出減小盲區的建議與策略。
(作者單位:江蘇省南京市第二十九中學初中部)

