基于自適應混合策略鯨魚優化算法的分數階PID控制器在液位控制中的研究

摘 要 為了進一步提高液位控制系統的控制精度和穩定性,采用分數階PID控制器(FOPID)對液位進行控制。由于分數階PID控制器存在整定參數多、整定困難等問題,提出了一種自適應混合策略鯨魚優化算法(AMSWOA)對分數階PID參數進行整定。采用實驗用單容和雙容水箱模擬工業中的液位控制。利用MATLAB工具對分數階PID控制器和液位控制系統進行仿真建模,并與整數階PID控制算法進行仿真比較。結果表明,與整數階PID控制器相比,應用自適應混合策略鯨魚優化算法的分數階PID控制器具有超調量小、調節時間短及穩態誤差小等優勢。
關鍵詞 液位控制 分數階PID控制 自適應混合策略鯨魚優化算法 仿真建模
中圖分類號 TP391.9"" 文獻標志碼 A"" 文章編號 1000 3932(2025)01 0016 06
在工業過程控制中,通常依靠人工經驗和經驗公式設定PID控制器參數來實現液位控制,從而達到預期的質量和產品安全水平,并使過程更加經濟[1]。但這種方法往往難以達到期望的控制效果,隨著計算機技術的不斷進步和液位控制精度的提高,國內外學者對液位控制進行了深入的研究,提出了一些新的控制方法。OMID S和AMIR T針對核蒸汽發生器的液位控制,通過粒子群優化(PSO)和遺傳算法(GA)對PID控制器參數進行整定[2],整定后穩態誤差、超調量均較小,穩定時間較短。GAO H等針對連鑄機中的模具液位控制系統,提出基于人工魚群優化算法的PID來調節模具液位[3]。與傳統PID控制器相比,利用人工魚群優化算法的PID控制其液位曲線波動明顯減少,系統魯棒性得到增強,進一步提高了連鑄機模具液位控制的質量。ELHOSSEINI M A等針對熱回收蒸汽發生器中的液位控制,提出人工蜂群優化(ABC)算法的分數階PID(Fractional Order Proportional Integral Derivative,FOPID)控制器[4],液位控制效果良好,但由于其數學計算復雜,不能很好地應用于工業實踐中。
學者們將優化算法與PID控制器進行結合,以提高PID控制器的控制性能。同時,一些學者將分數階PID控制器應用在液位控制中,這種方法在液位控制中的應用可以有效提高控制效果和系統穩定性。為了進一步提高液位控制性能,筆者設計了一種自適應混合策略鯨魚優化算法(Adaptive Mixed Strategy Whale Optimization Algorithm,AMSWOA)的分數階PID控制器。利用實驗用水箱做液位特性實驗分別得到單容、雙容水箱傳遞函數,在MATLAB/Simulink環境下搭建智能控制器和液位控制系統仿真模型,并與整數階PID控制算法進行比較,由此實現單容、雙容水箱液位系統控制器的設計及液位的控制。
1 自適應混合策略鯨魚優化算法的分數階PID控制器設計
1.1 分數階PID控制器
分數階PID控制器相較于整數階PID控制器,除具有K、K、K3個可調節系統性能的參數外,還增加了兩個參數,即一個積分階次λ和一個微分階次μ[5]。其中,λ和μ可以取(0,2)內的任意實數。圖1是分數階PID控制器階次λ與μ的取值范圍。
分數階PID控制器的傳遞函數C(s)為:
C(s)==K+Ks+Ks" (1)
其中,K為比例增益,K為積分增益,K為微分增益,U(s)是控制器的輸出,E(s)是控制器的誤差輸入。
分數階PID控制系統結構如圖2所示,其中,
G(s)表示被控對象的傳遞函數,R(s)表示輸入量,Y(s)表示輸出量。
1.2 自適應混合策略鯨魚優化算法的實現
針對普通鯨魚優化算法搜索精度低、收斂速度較慢及容易陷入局部最優解等缺點進行改進,在鯨魚優化算法的基礎上引入Tent混沌序列[6]以初始化種群,在一定程度上提高種群的多樣性,有助于提高算法的搜索能力和收斂速度;同時,加入自適應權重提高鯨魚優化算法的全局搜索和局部搜索能力[7];還引入了高斯變異以提高算法的搜索精度[8]。自適應混合策略鯨魚優化算法流程如圖3所示。
2 數學建模及仿真
2.1 單容水箱液位控制
2.1.1 數學模型
單容水箱以YB2000型過程實驗裝置為依托,其實驗原理如圖4所示。
圖中被控對象即水箱液位為h,控制量(輸入量)是水箱的進水量Q,Q為水箱的出水量,出水閥V固定于某一開度值。根據物料動態平衡的關系,任何時刻水位變化均滿足:
Q-Q=0(2)
其中,Q為穩態時水箱進水量,Q為穩態時水箱出水量。
動態時,則有:
Q-Q=(3)
其中,V為水箱的貯水容積,dV/dt為水貯存量的變化率,它與h的關系為dV=Adh,即:
=A(4)
其中,A為水箱的底面積。
由式(3)、(4)得:
Q-Q=A(5)
基于Q=h/R,R為閥門V的液阻,則式(5)可以改寫為:
Q-=A(6)
即:
=(7)
其中,T為過程的時間常數,T=AR,它與水箱的底面積A和閥門V的液阻R有關;K為過程的放大系數,K=R。式(7)為單容水箱的傳遞函數。令Q=R/s,R為常量,則式(7)可改為:
H(s)=×=K-(8)
對式(8)求拉氏變換,得:
h(t)=KR(1-e)(9)
當t=∞時,有:
K=h(∞)/R=輸出穩態值/階躍輸入(10)
當t=T時,有:
h(t)=KR(1-e)=0.632KR=0.632h(∞)(11)
式(9)表示一階慣性環節的階躍響應曲線是單調上升的指數函數。因為大多工業控制都帶有一定的滯后,設純滯后時間為τ,所以單容水箱的數學模型表示為:
=e(12)
依據實驗數據,已知輸出穩態值h(∞)=39.5366,階躍輸入R=20,根據式(10)解得K=1.9768。根據單容水箱液位數學建模實驗原理,時間常數T是該曲線到穩態值時間的63%處的時間,由于0.632h(∞)=24.9871,因此T的值為1 207 s。由于單容水箱液位特性實驗響應有60 s的滯后時間,因此得到被控對象水箱的傳遞函數:
G(s)=e(13)
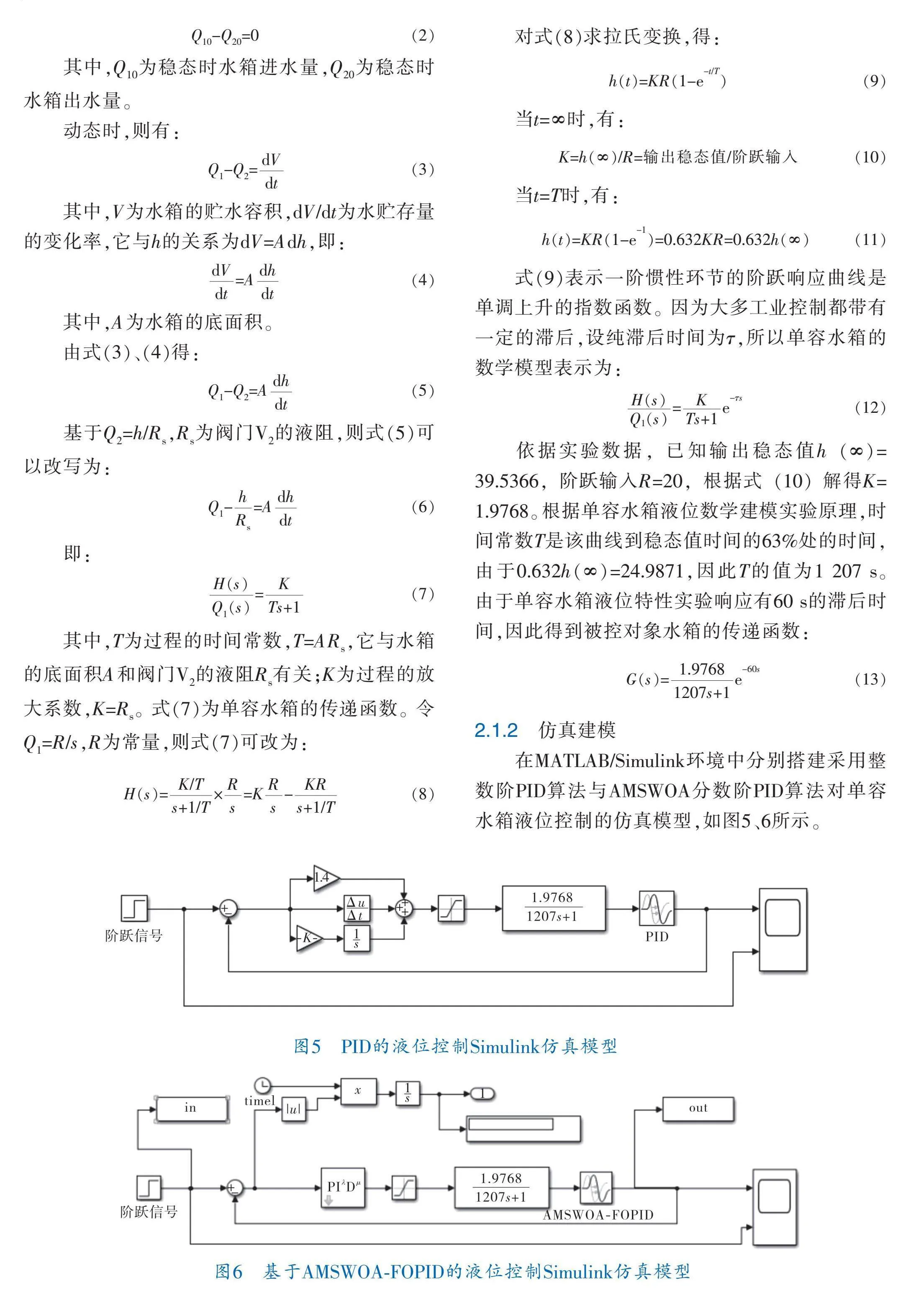
2.1.2 仿真建模
在MATLAB/Simulink環境中分別搭建采用整數階PID算法與AMSWOA分數階PID算法對單容水箱液位控制的仿真模型,如圖5、6所示。
2.1.3 仿真結果分析
由于算法在優化過程中存在一定的隨機性,多次運行算法程序,選取最優運行效果。在進行仿真實驗前,需要對相關參數進行設置,整數階PID控制器采用Z N法對控制器參數進行整定;AMSWOA算法有關參數設置為鯨魚規模50,算法迭代最大值10,收斂因子a的初始值(a)為2,a的終止值(a)為1,非線性調節系數m為0.1。其他參數隨機初始化,通過分析多次實驗結果發現,當整定參數的取值范圍KP∈[0,10],K∈[0,10],K∈[0,10],λ、μ∈[0,2]時控制效果良好。相應的控制參數設置完之后,點擊運行按鈕程序自動運行進行對比實驗,兩種控制算法對單容水箱液位控制的效果如圖7、8所示。
結果表明,相較于整數階PID控制器,筆者設計的AMSWOA FOPID方法對單容水箱液位控制具有上升時間短、超調量小、穩態誤差小與調節時間短的優勢。
2.2 雙容水箱液位控制
雙容水箱液位系統與工業生產中的被控對象具有相似的耦合性、滯后性及非線性等特性。筆者采用AE2000過程控制實驗裝置進行雙容水箱液位控制的研究。
2.2.1 數學模型
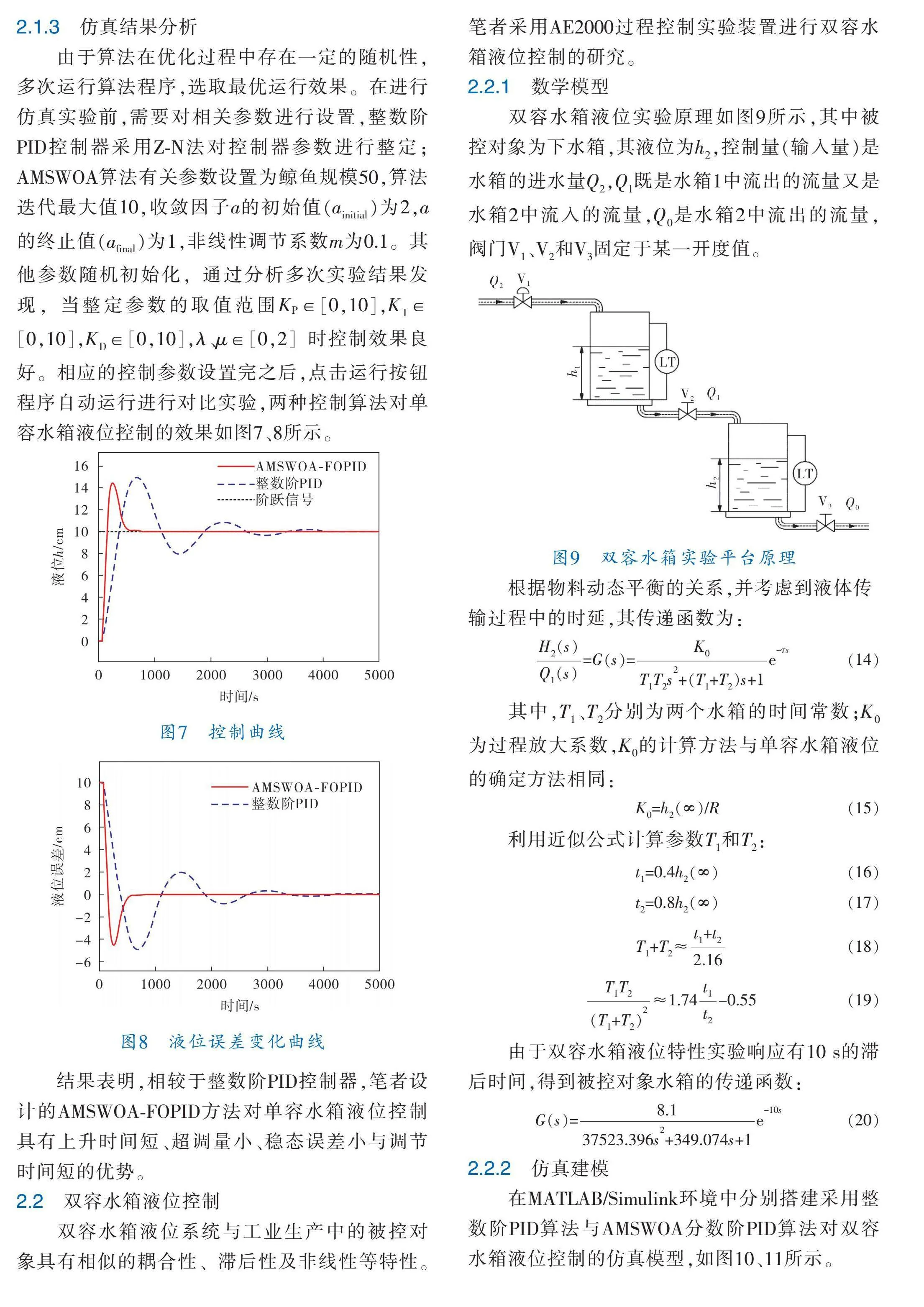
雙容水箱液位實驗原理如圖9所示,其中被
控對象為下水箱,其液位為h,控制量(輸入量)是水箱的進水量Q,Q既是水箱1中流出的流量又是水箱2中流入的流量,Q是水箱2中流出的流量,閥門V、V和V固定于某一開度值。
根據物料動態平衡的關系,并考慮到液體傳輸過程中的時延,其傳遞函數為:
=G(s)=e(14)
其中,T、T分別為兩個水箱的時間常數;K為過程放大系數,K的計算方法與單容水箱液位的確定方法相同:
K=h(∞)/R(15)
利用近似公式計算參數T和T:
t=0.4h(∞)(16)
t=0.8h(∞)(17)
T+T≈(18)
≈1.74-0.55(19)
由于雙容水箱液位特性實驗響應有10 s的滯后時間,得到被控對象水箱的傳遞函數:
G(s)=e "(20)
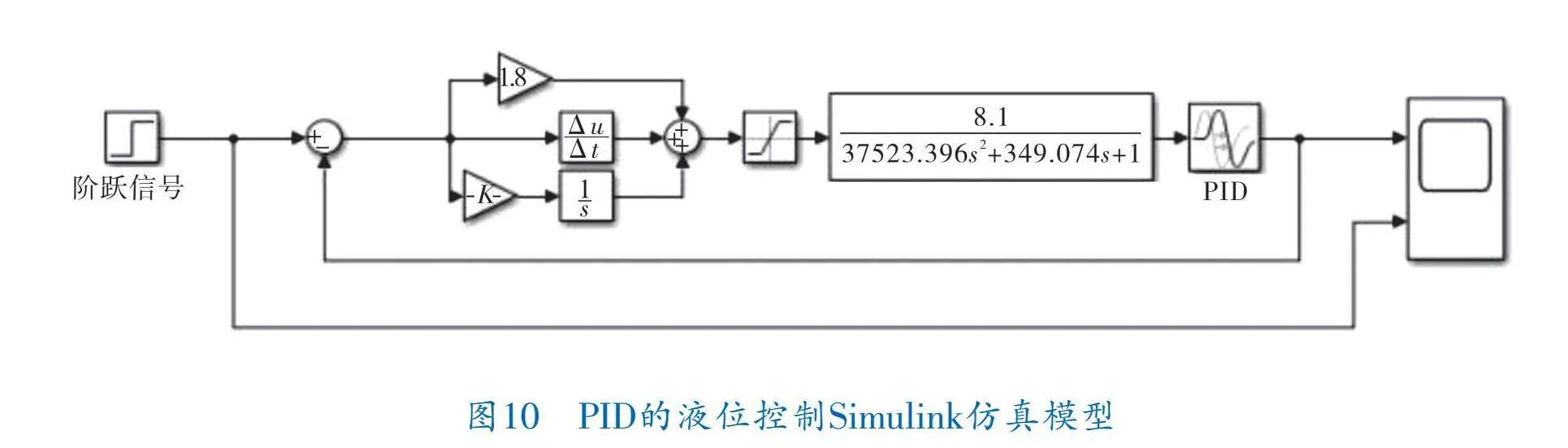
2.2.2 仿真建模
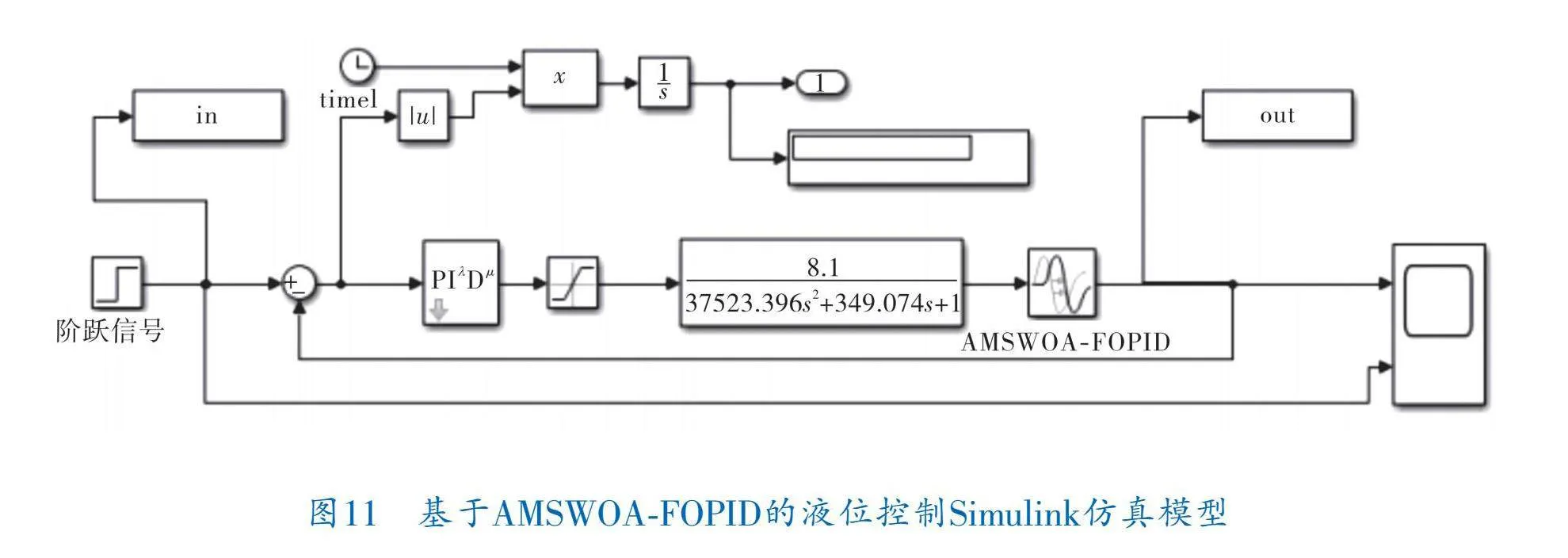
在MATLAB/Simulink環境中分別搭建采用整數階PID算法與AMSWOA分數階PID算法對雙容水箱液位控制的仿真模型,如圖10、11所示。
2.2.3 仿真結果分析
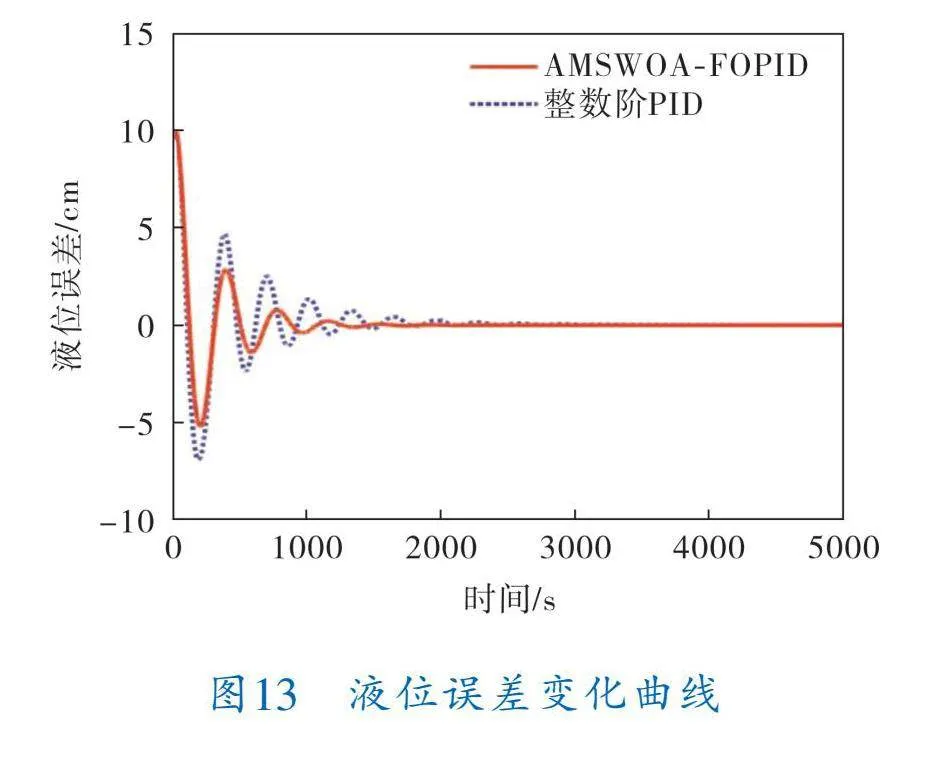
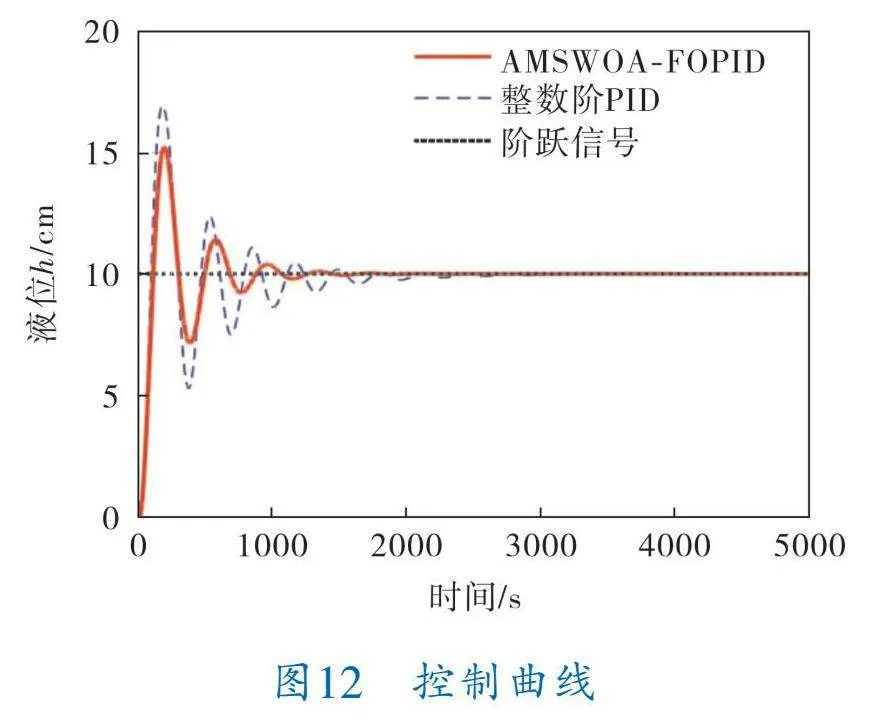
對相應的控制參數進行設置后,兩種控制算法對雙容水箱液位控制的控制效果如圖12、13所示。
由圖12可以看出,PID控制曲線的超調量要大于AMSWOA FOPID控制曲線的;調節時間上,AMSWOA FOPID控制曲線明顯優于PID控制曲線;上升時間上,PID控制曲線與AMSWOA FOPID控制曲線相差不多。
由圖13可以看出,采用整數階PID控制器的控制誤差變化波動大,而使用AMSWOA FOPID進行控制,誤差變化相對平緩。
3 結束語
利用實驗平臺做水箱液位特性實驗,分別得到YB2000過程控制實驗裝置的單容水箱傳遞函數與AE2000過程控制實驗裝置的雙容水箱傳遞函數;然后,分別將筆者提出的AMSWOA FOPID控制器與整數階PID控制器應用在單容水箱與雙容水箱液位控制上進行仿真實驗,經分析分析得到AMSWOA FOPID控制的液位曲線在超調量、調節時間與穩態誤差上都優于整數階PID控制的,液位控制性能得到較大的提升。文中的研究將對工業生產中的液位過程控制研究起到參考和指導作用。
參 考 文 獻
[1] YAHYA S,JADMIKO S W,WIJAYANTO K,et al.Design and implementation of training module for control liquid level on tank using PID method based PLC[J].IOP Conference Series:Materials Science and Engineering,2020,830(3):032065.
[2]" OMID S,AMIR T.Optimization of PID controller for water level control of the nuclear steam generator using PSO and GA[J].Kerntechnik,2022,87(5):597-606.
[3]" GAO H,HAO P,LIU S.Application of Artificial Fish Swarm PID in Mold Level Control of Continuous Casting Machine[C]//2020 5th International Conference on Mechanical,Control and Computer Engineering(ICMCCE).Piscataway,NJ:IEEE,2020:592-596.
[4]"" ELHOSSEINI M A,SHAMS EL DIN A,ALI H A,et al.Heat recovery steam generator (HRSG) three element drum level control utilizing Fractional order PID and fuzzy controllers[J].ISA Transactions,2022,122(1):281-293.
[5]"" PODLUBNY I.Fractional order system and PID contro
llers[J].IEEE Transactions on Automatic Control,1999,44(1):208-214.
[6]"" XIAO L.Parameter tuning of PID controller for beer filling machine liquid level control based on improved genetic algorithm[J].Computational Intelligence and Neuroscience,2021(1):1-10.
[7]"" ZHANG J,WANG J S.Improved Whale Optimization Algorithm Based on Nonlinear Adaptive Weight and Golden Sine Operator[J].IEEE Access,2020,8:77013-77048.
[8]"" ROSENTHAL K I.Quantales and their applications[M].London:Longman Scientific and Technical,1990.
(收稿日期:2024-01-11,修回日期:2024-12-10)
The Fractional Order PID Controller for Liquid Level Control Based on Adaptive Mixed Strategy Whale Optimization Algorithm
LU Qi1, ZHANG Yan li2, LI Xin hua2, WANG Ming chao1
(1. Dandong Dongfang Measurement and Control Technology Co., Ltd.;
2. Panjin Institute of Industrial Technology, Dalian University of Technology)
Abstract"" With a view to improving the control accuracy and stability of the liquid level control system, the fractional order proportional integral derivative(FOPID) controller was applied there. Considering the FOPID’s many adjustment parameters and its difficulty to adjust, the adaptive mixed strategy whale optimization algorithm(AMSWOA)was proposed for FOPID parameter tuning. In the experiment, both single and double tanks were adopted to simulate the liquid level control in the industry, including having the Matlab tool employed to simulate and model both FOPID controller and liquid level control system, and then having it compared with the integer order PID controller in simulation. The simulation and experimental results show that, the FOPID controller based on AMSWOA, as compared to integral order PID controller, boasts small overshoot, quick adjustment time and low steady state error.
Key words"" liquid level control, FOPID control, AMSWOA, simulation modeling

