基于LGRSAE算法的非線性化工過程故障檢測

摘 要 針對常規線性降維方法不能有效提取實際復雜非線性工業數據局部和全局結構特征的問題，提出一種局部和全局保持堆棧自編碼器（LGRSAE）以及基于LGRSAE的過程故障檢測方法。在自編碼器（AE）的目標函數中引入局部保持投影（LPP）算法和主成分分析（PCA）算法的目標約束構造局部和全局結構保持自編碼器（LGRAE），以提取數據局部和全局結構相關的特征。為了提取過程數據深層局部和全局結構相關的特征，將LGRAE堆棧構成LGRSAE。在田納西－伊斯曼（TE）過程數據集的故障檢測結果表明，LGRSAE的特征提取方法平均故障檢測率高于MRSAE、KPCA算法，且誤報率更低。

關鍵詞 故障檢測 堆棧自編碼器 特征提取 局部和全局結構保持 數據降維

中圖分類號 TP277"" 文獻標志碼 A"" 文章編號 1000 3932（2025）01 0111 08

工業過程故障檢測最主要的目的是能夠迅速地檢測出可能影響過程安全或者產品質量的異常變化［1］。多元統計監控方法的本質是基于數據驅動的故障檢測方法，主要的基于數據驅動的方法有：主成分分析（Principal Component Analysis，PCA）［2］、偏最小二乘法（Partial Least Square，PLS）［3］和獨立成分分析（Independent Component Analysis，ICA）［4］。上述方法使用線性降維會丟失數據局部信息，而局部保留投影（Locality Preserving Projection，LPP）算法［5］雖能提取數據的局部特征，但對于復雜分布的非線性過程表現不佳。

非線性特征提取方法有：基于核函數的方法、基于機器學習的方法和基于深度學習的方法。最經典的基于核函數的方法是核主元分析（Kernel Principal Component Analysis，KPCA）［6］。KPCA使用核函數將數據投影到高維空間，在高維空間進行特征提取。KPCA考慮了數據的非線性特征，對于非線性數據的故障檢測效果要優于線性降維方法。機器學習特征提取方法有高斯混合模型（Gaussian Mixture Model，GMM）［7］、支持向量機（Sport Vector Machine，SVM）［8］及支持向量描述（Support Vector Data Description，SVDD）［9］等。基于深度學習的非線性特征提取方法是近幾年的研究熱點。基于深度學習的特征提取算法主要包括：卷積神經網絡（Conventional Neural Network，CNN）［10］、深度置信網絡（Deep Brief Network，DBN）［11］、堆棧自編碼器（Stacked Auto Encoder，SAE）［12］及堆棧降噪自編碼器（Stacked Diagnosing Auto Encoder，SDAE）［13］等。

堆棧自編碼器（Stacked Auto Encoder，SAE）采用分層預訓練和超參數微調的策略，在重構數據時提取數據的深層特征。SAE算法若將激活函數選為線性激活函數，則可達到PCA算法的效果，若選擇非線性激活函數，則可用于非線性特征降維，類似于KPCA算法。常規SAE算法僅考慮了數據的全局結構，未能同時考慮數據的局部和全局結構信息，特征提取能力還有待進一步提高。在復雜的化工過程數據中，需要SAE在學習到的特征中保留數據的局部和全局結構特征。為了解決這一問題，筆者提出了一種局部全局保持堆棧自編碼器（Local and Global Structure Preserving Regularized Stacked Auto Encoder，LGRSAE），以逐層保持原始輸入數據的局部和全局結構。最后，通過田納西－伊斯曼（Tennessee Eastman，TE）過程驗證了LGRSAE算法的有效性。

1 局部全局結構保持堆棧自編碼器

給定訓練數據X=［x，x，…，x］，x∈R，n為采樣點個數，m為樣本個數，編碼器通過非線性變換f（·）將訓練數據x投影到隱含層h，解碼器使用非線性變換f（·）將h重構輸出為，數學表達式如下：

h=f（W（e）x+b（e））""""" （1）

=f（Wh+b） """""""" """ （2）

其中，f（·）和f（·）分別是編碼環節和解碼環節的激活函數，W和W分別是編碼環節和解碼環節的權重矩陣，b和b分別是編碼環節和解碼環節的偏差向量。

自編碼器AE通過訓練找到使訓練誤差最小的最優參數集合θ=｛W，W，b，b｝：

J（θ）=‖-x‖""" （3）

其中，J（θ）為自編碼器的均方誤差訓練目標函數。

LPP是非線性拉普拉斯特征映射的線性近似，目的在于保持數據的局部拓撲結構。如果兩數據點x和x在高維空間中相鄰，那么對應的點h和h在投影空間中仍是相鄰的。LPP目標函數為：

J=min‖h-h‖M""" （4）

其中，h=Lx，L為LPP的投影矩陣。M為數據點x和x的近鄰權重，可以用熱核函數表示：

M=e，x∈N（x）或x∈N（x）0"""" ，其他" （5）

其中，δ為可調參數，可控制權重隨距離增大而遞減；N（x）和N（x）分別為x和x的k近鄰數據點集合。

PCA以線性變換將高維數據x按最大化數據方差的方向投影到低維特征空間時，h保留了數據x最大全局結構。PCA目標函數為：

J=max‖h-h‖"""" （6）

其中，h=Px，P為PCA的投影矩陣。

為了在AE算法數據重構的過程中保留數據的局部、全局結構，從而提取數據局部、全局結構相關的特征，將LPP算法和PCA算法的目標函數引入AE算法，構造局部全局結構保持自編碼器（Local and Global Structure Preserving Regularized Auto Encoder，LGRAE）。為了提取數據的局部和全局結構特征，若兩個數據距離足夠近，它們在LGRAE的重構空間中也要足夠近。在LGRAE重構空間最大化數據的方差，以提取數據的潛在全局結構特征。LGRAE的目標函數定義如下：

min J（θ）=min J+λ"" （7）

J（θ）=‖-‖M""" （8）

J（θ）=‖-x‖"""" （9）

其中，λ為非負常數；ε為非負微小常數；x為樣均值本；J為重構損失；J（θ）為局部方差損失，可使數據點x和x的近鄰關系在LGRAE重構空間和中得以保留；J（θ）為全局方差損失，可使重構空間按照原始數據最大化方差的投影方向構造，以在LGRAE的重構過程中提取數據的全局結構特征。LGRAE的結構如圖1所示。

2 LGRSAE參數更新方式

以第i個數據x為例，LGRAE的隱含層為h，重構數據為。LGRAE的參數θ通過反向傳播算法（BP）更新，直至達到設定迭代次數，或者最小設定誤差。更新迭代方式如下。

a. 計算LGRAE前向傳播的隱含層輸出h和重構數據：

z=Wx+b""""" （10）

h=f（z）"""""" （11）

z=Wx+b""""" （12）

=f（z）"""""" （13）

其中，z為h的激活輸入，z為的激活輸入。

b. 根據式（3）、（8）、（9）計算LGRAE的重構損失J、局部方差損失J和全局方差損失J，然后基于損失函數（7）計算偏導數：

=

=-（-x）？茚f ′（z）+λ（（-）M？茚（ε+‖-x‖）-

‖-‖M？茚（-x））？茚f ′（z）/（‖-x‖+ε）

（14）

其中，f ′為激活函數f的導數，？茚表示矩陣的逐元素乘積。

c. 計算J對隱含層h的輸入z的偏導數δ：

δ=

=（w（d））？茚f ′（z）"""" （15）

其中，f ′為激活函數f的導數。

d. LGRAE的參數可由反向傳播算法進行自動更新：

w=w-η=W-hTi

b=b-η=b-

w=w-η=W-xTi

b=b-η=b-"nbsp;" （16）

其中，η為LGRAE的學習率。

LGRSAE（圖2）是由l個LGRAE構成的。

AE——第i個預訓練的AE；——第i個AE的重構輸出；

h——第i個AE的潛隱變量（隱含層）

LGRSAE的訓練包括兩個步驟：無監督預訓練和參數微調。無監督預訓練首先訓練LGRAE，求得最優參數集合W、W、b、b以及隱含層h，將h作為LGRAE輸入，訓練LGRAE。依次訓練LGRAE～LGRAE可以得到LGRSAE的參數集合｛W｝、｛W｝、｛b｝、｛b｝，將其作為LGRSAE參數微調階段的初始化參數。令第1個LGRAE的訓練輸入x和重構輸出分別為h和，第l個LGRAE的訓練輸入h和重構輸出之間的損失函數為：

J（θ）=‖-h‖+

λ""""" （17）

LGRSAE是將LGRAE1～LGRAEl中的節點按照［x，h，…，h，h，，…，，］的順序進行堆棧連接構成的。在LGRSAE初始化參數的基礎上繼續訓練可得到訓練好的模型。

3 基于LGRSAE的過程檢測

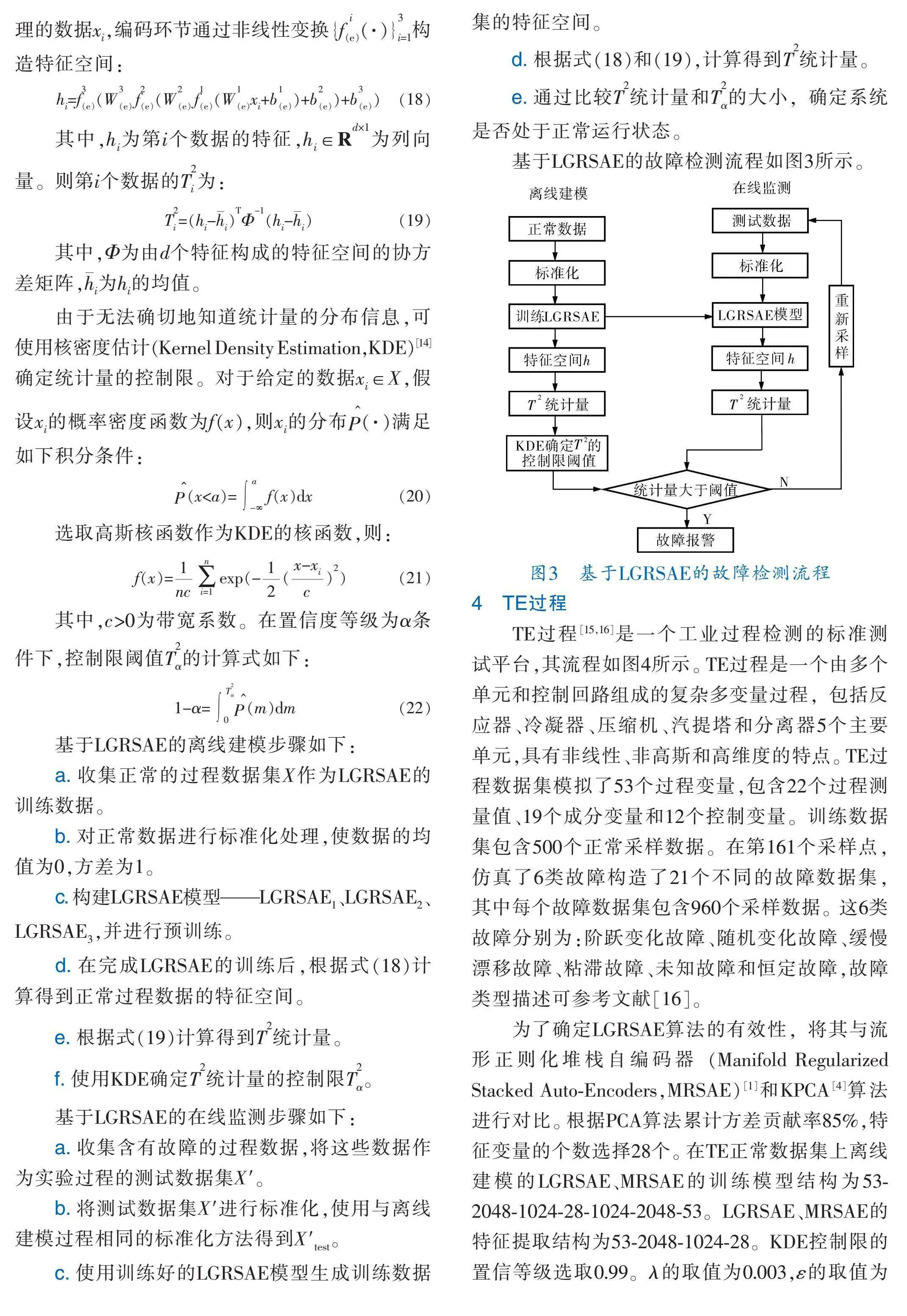
以3個LGRAE構成的LGRSAE為例，｛W｝和｛b｝分別為第i個LGRAE編碼環節的權值和偏差值，其特征空間計算步驟如下：對于第i個預處理的數據x，編碼環節通過非線性變換｛f（·）｝構造特征空間：

h=f（Wf（Wf（Wx+b）+b）+b） （18）

其中，h為第i個數據的特征，h∈R為列向量。則第i個數據的T為：

T=（h-h）Φ（h-h）"""" （19）

其中，Φ為由d個特征構成的特征空間的協方差矩陣，h為h的均值。

由于無法確切地知道統計量的分布信息，可使用核密度估計（Kernel Density Estimation，KDE）［14］確定統計量的控制限。對于給定的數據x∈X，假設x的概率密度函數為f（x），則x的分布（·）滿足如下積分條件：

（xlt;a）= f（x）dx"""" （20）

選取高斯核函數作為KDE的核函數，則：

f（x）=exp（-（））"" （21）

其中，cgt;0為帶寬系數。在置信度等級為α條件下，控制限閾值T的計算式如下：

1-α=（m）dm""""" （22）

基于LGRSAE的離線建模步驟如下：

a. 收集正常的過程數據集X作為LGRSAE的訓練數據。

b. 對正常數據進行標準化處理，使數據的均值為0，方差為1。

c. 構建LGRSAE模型——LGRSAE、LGRSAE、LGRSAE，并進行預訓練。

d. 在完成LGRSAE的訓練后，根據式（18）計算得到正常過程數據的特征空間。

e. 根據式（19）計算得到T統計量。

f. 使用KDE確定T統計量的控制限T。

基于LGRSAE的在線監測步驟如下：

a. 收集含有故障的過程數據，將這些數據作為實驗過程的測試數據集X′。

b. 將測試數據集X′進行標準化，使用與離線建模過程相同的標準化方法得到X′。

c. 使用訓練好的LGRSAE模型生成訓練數據集的特征空間。

d. 根據式（18）和（19），計算得到T統計量。

e. 通過比較T統計量和T的大小，確定系統是否處于正常運行狀態。

基于LGRSAE的故障檢測流程如圖3所示。

4 TE過程

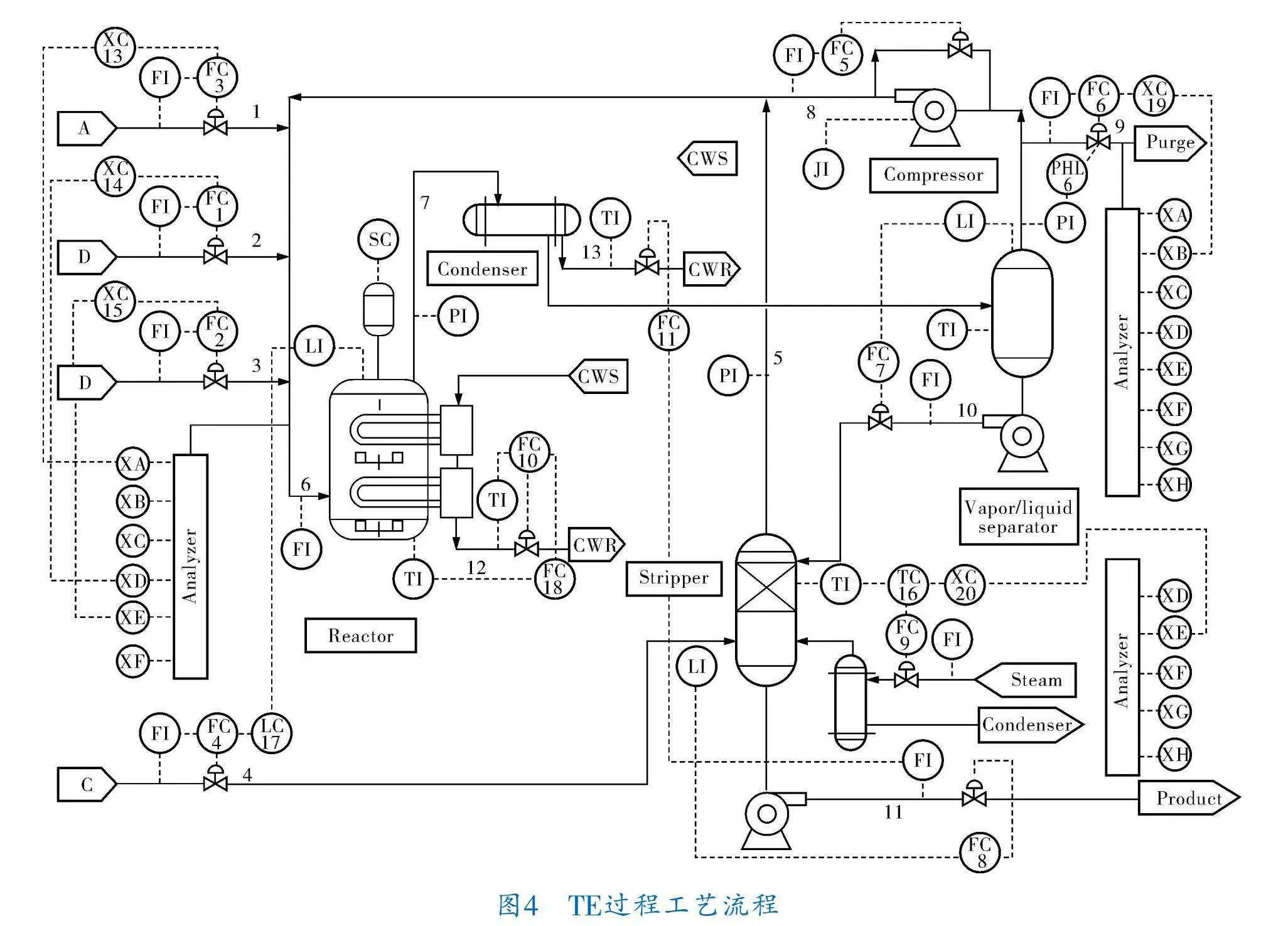
TE過程［15，16］是一個工業過程檢測的標準測試平臺，其流程如圖4所示。TE過程是一個由多個單元和控制回路組成的復雜多變量過程，包括反應器、冷凝器、壓縮機、汽提塔和分離器5個主要單元，具有非線性、非高斯和高維度的特點。TE過程數據集模擬了53個過程變量，包含22個過程測量值、19個成分變量和12個控制變量。訓練數據集包含500個正常采樣數據。在第161個采樣點，仿真了6類故障構造了21個不同的故障數據集，其中每個故障數據集包含960個采樣數據。這6類故障分別為：階躍變化故障、隨機變化故障、緩慢漂移故障、粘滯故障、未知故障和恒定故障，故障類型描述可參考文獻［16］。

為了確定LGRSAE算法的有效性，將其與流形正則化堆棧自編碼器（Manifold Regularized Stacked Auto Encoders，MRSAE）［1］和KPCA［4］算法進行對比。根據PCA算法累計方差貢獻率85%，特征變量的個數選擇28個。在TE正常數據集上離線建模的LGRSAE、MRSAE的訓練模型結構為53 2048 1024 28 1024 2048 53。LGRSAE、MRSAE的特征提取結構為53 2048 1024 28。KDE控制限的置信等級選取0.99。λ的取值為0.003，ε的取值為0.001。仿真環境為：CPU Inter（R） Core （TM） i7 9700H，操作系統 Windows 10（64位），RAM 16 GB，軟件 Python 3.8.5、TensorFlow 2.5.0。

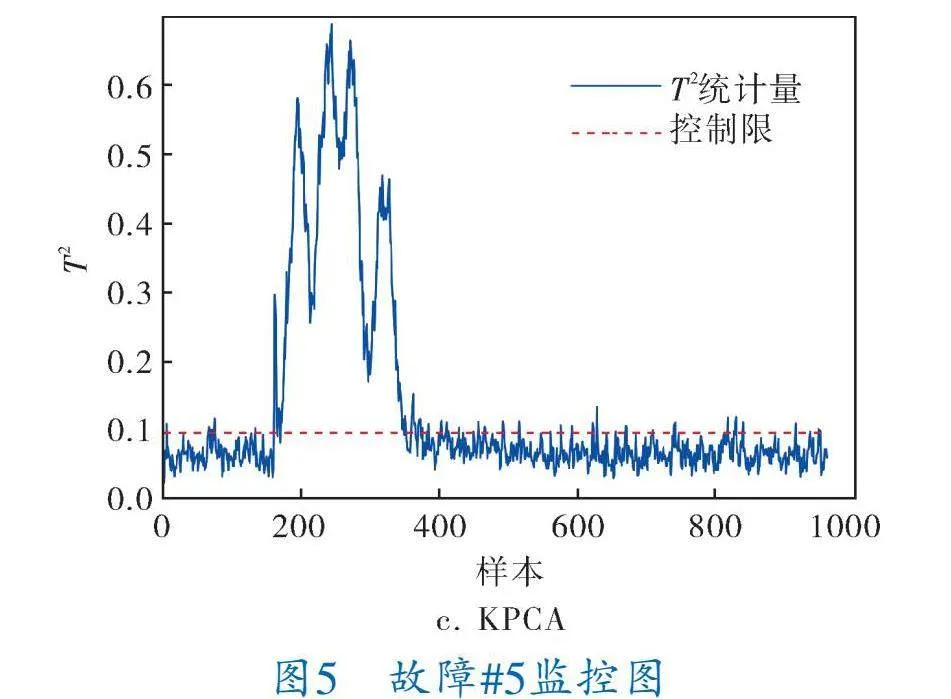
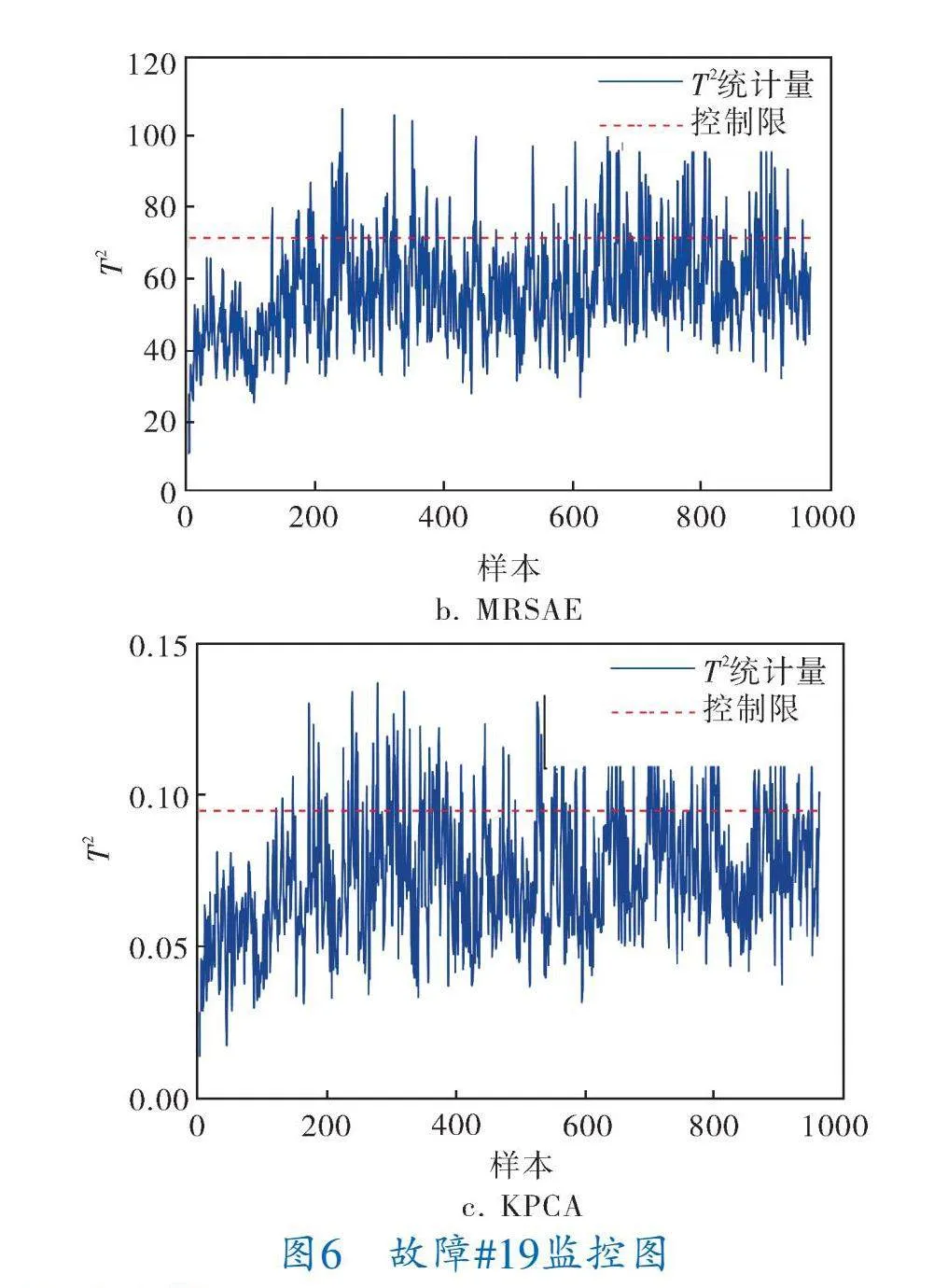
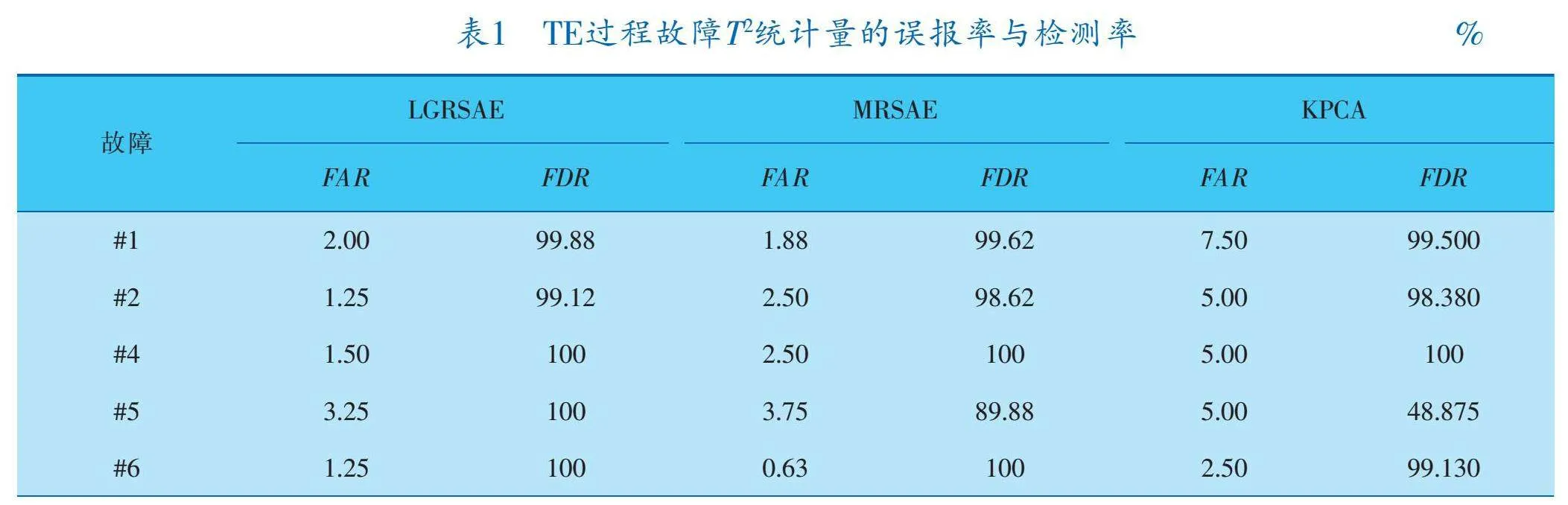
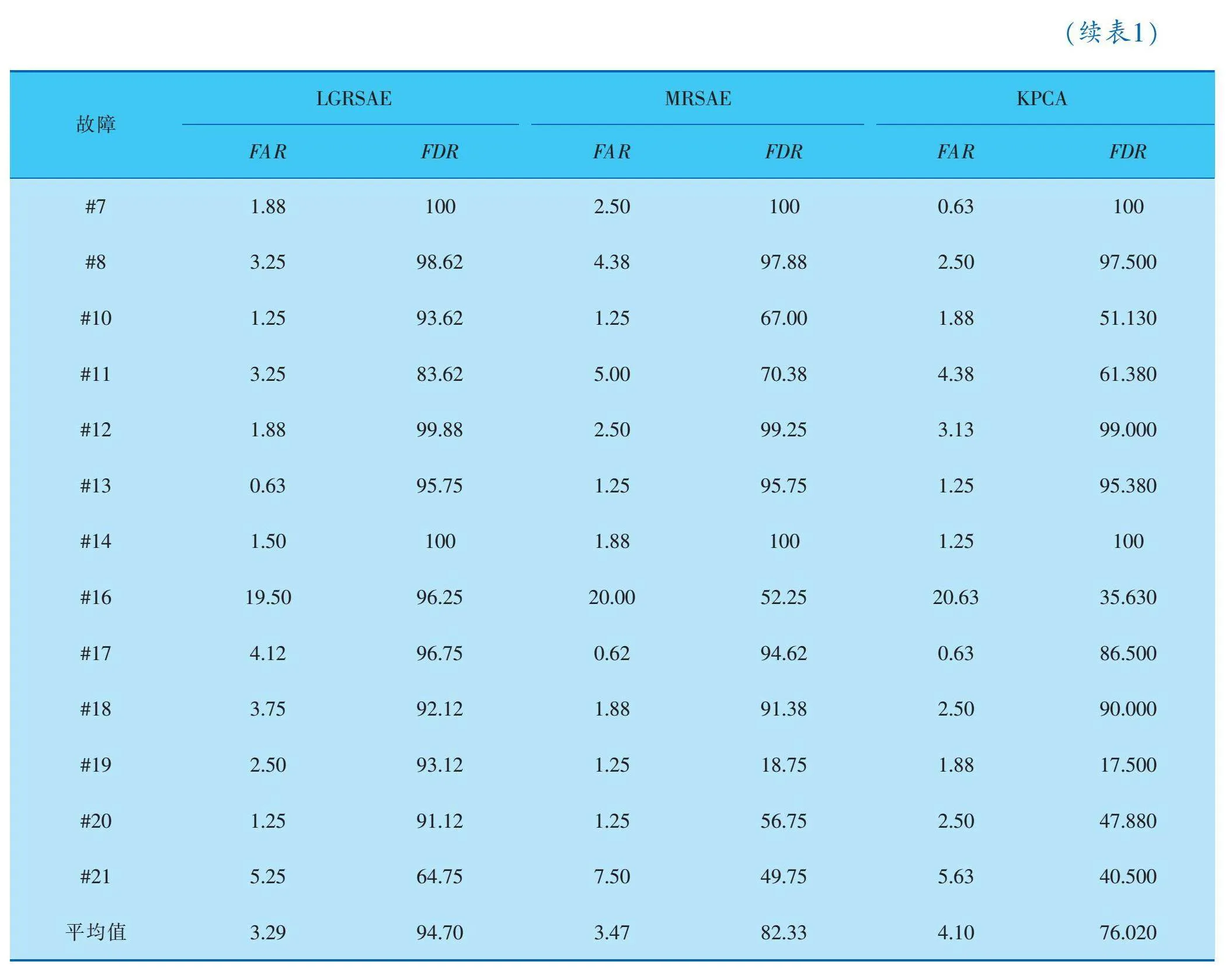
算法故障性能指標為檢測率FDR和誤報率FAR。表1給出了3個算法的仿真結果，故障#3、#9、#15的檢測效果較差，將其排除在外［1］。LGRSAE的平均FAR為3.29%，較MRSAE和KPCA分別低0.18%和0.81%，LGRSAE平均FDR為94.7%，較MRSAE和KPCA分別高12.37%和18.68%，而MRSAE的FDR僅優于KPCA算法6.31%。根據統計結果來看，LGRSAE在FAR和FDR上表現都最好，其次是MRSAE算法，KPCA算法表現最差。由于LGRSAE在目標函數中引入數據局部和全局結構保持的正則化，可學習數據間更有用的潛在流形結構相關特征，因此故障檢測效果優于MRSAE和KPCA。

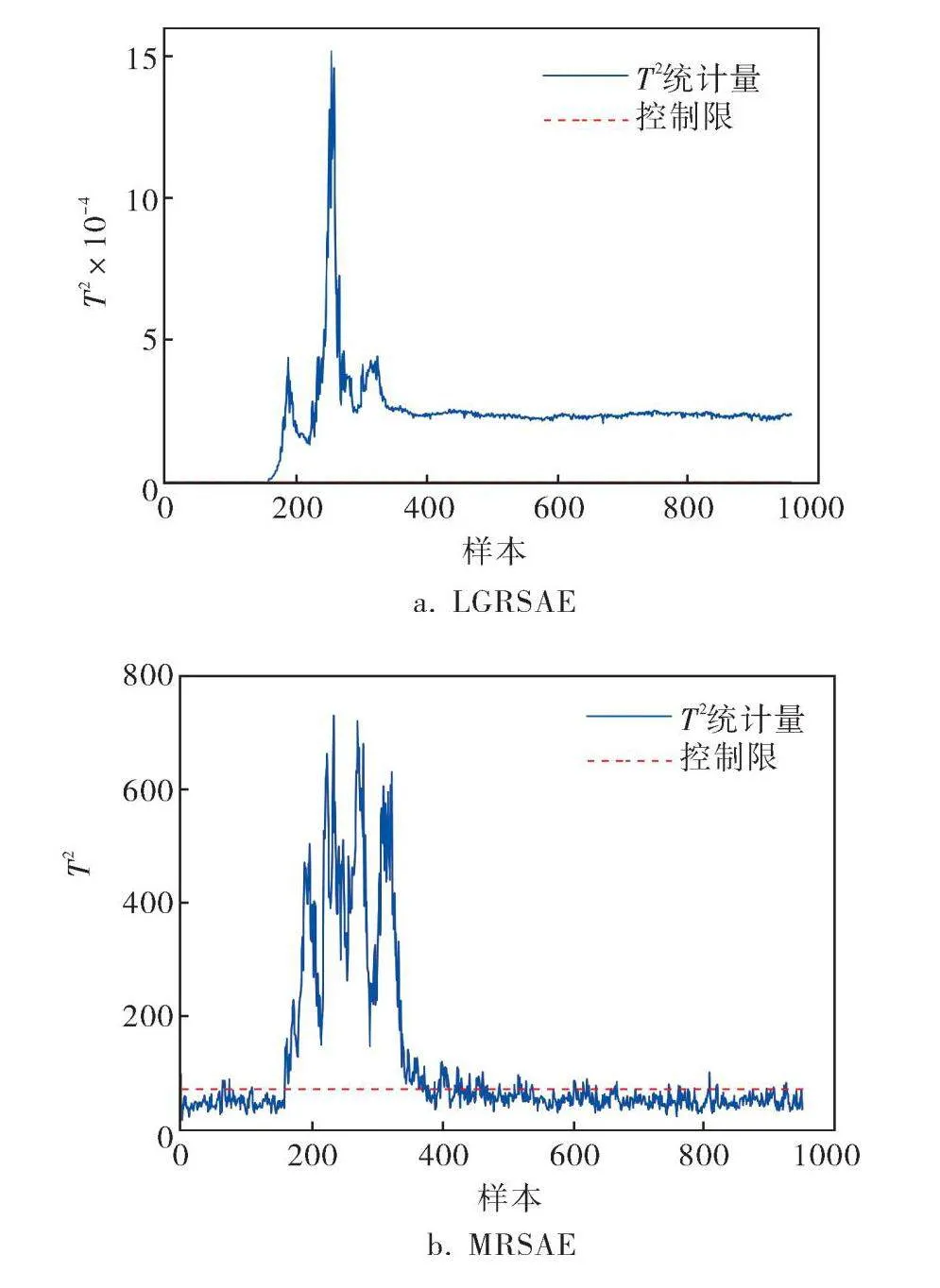
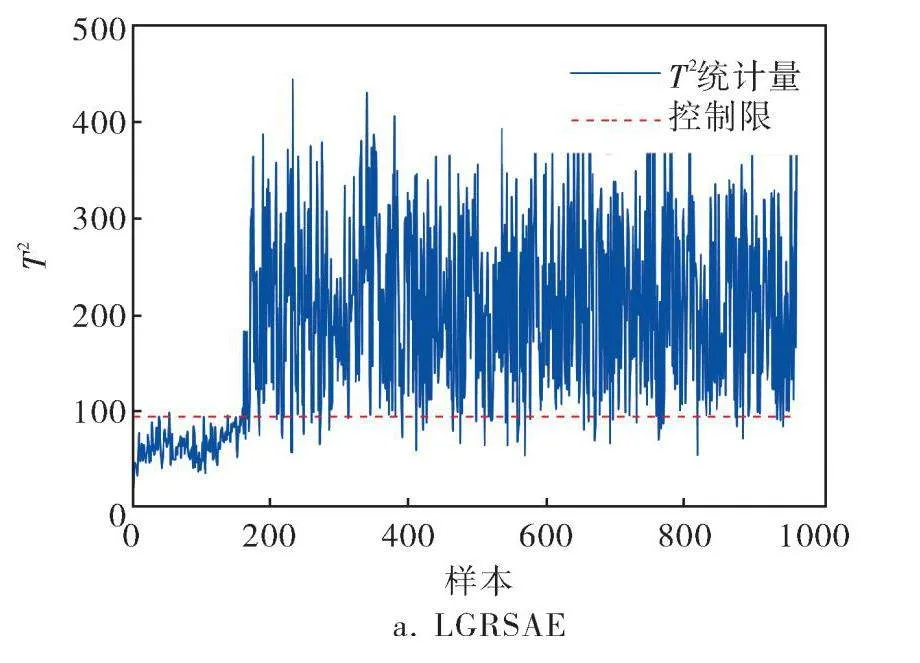
LGRSAE在故障#5、#10、#16、#19、#20表現出較高的檢測率（分別為100%、93.62%、96.25%、93.12%、91.12%），而其他算法對于這5個故障的檢測率都不到80%。故障#5、故障#19的檢測結果如圖5、6所示，LGRSAE和MRSAE方法的FDR均顯著優于KPCA。從圖5、6中可以看出，LGRSAE的T2統計量在故障出現后幾乎同時超過控制限，可以反映出LGRSAE對于故障的靈敏性。

5 結束語

LGRSAE結合了LPP和PCA算法的思想，并在重構空間中保留了數據的局部和全局結構，可以提取數據間的潛在局部和全局結構相關特征。通過LGRSAE進行特征提取，構造T2統計量進行故障檢測。在TE過程數據集中，LGRSAE的T2統計量能夠有效地捕捉到故障引起的過程變量異常，從而實現對故障的準確檢測。LGRSAE的T2統計量在TE過程數據集上有94.7%的平均檢測率，LGRSAE在多個故障類型上要優于對照算法。LGRSAE引入正則化能夠使模型提取非線性數據間流形結構相關的特征，誤報率低于MRSAE和KPCA算法，具有更高的魯棒性。

參 考 文 獻

［1］ YU J B，ZHANG C Y.Manifold regularized stacked aut "oencoders based feature learning for fault detection in industrial processes［J］.Journal of Process Control，2020，92（1）：119-136.

［2］ 王海清，宋執環，王慧.PCA過程監測方法的故障檢測行為分析［J］.化工學報，2002，53（3）：297-301.

［3］ 常鵬，高學金，王普.基于多向核熵偏最小二乘的間歇過程監測及質量預測［J］.北京工業大學學報，2014，40（6）：851-856.

［4］ JIANG Q，YAN X，LV Z，et al.Independent component analysis based nonGaussian process monitoring with preselecting optimal components and support vector data description［J］.International Journal of Production Research，2014，52（11）：3273-3286.

［5］ 郭金玉，仲璐璐，李元.基于統計差分LPP的多模態間歇過程故障檢測［J］.計算機應用研究，2019，36（1）：123-126.

［6］ LEE J M，YOO C K，CHOI S W，et al.Nonlinear process monitoring using kernel principal componentanalysis［J］.Chemical Engineering Science，2004，59（1）：223-234.

［7］ 譚帥，常玉清，王福利，等.基于GMM的多模態過程模態識別與過程監測［J］.控制與決策，2015，30（1）：53-58.

［8］ 許潔，胡壽松.基于KPCA和MKL SVM的非線性過程監控與故障診斷［J］.儀器儀表學報，2010，31（11）：2428-2433.

［9］ KIM Y，KIM S B.Optimal 1 alarm controlled support vector data description for multivariate process monitoring［J］.Journal of Process Control，2018，65（1）：1-14.

［10］ 李元，馮成成.基于一維卷積神經網絡深度學習的工業過程故障檢測［J］.測控技術，2019，38（9）：36-40；61.

［11］ SALAKHUTDINOV R，HINTON G.An Efficient Learn ing Procedure for Deep Boltzmann Machines［J］.Neural Computation，2012，24（8）：1967-2006.

［12］ LI Z C，TIAN L，JIANG Q C，et al.Distributed ensem ble stacked autoencoder model for non linear process monitoring［J］.Information Sciences，2020， 542（1）：302-316.

［13］ VINCENT P，LAROCHELLE H，LAJOIE I，et al.Stac "ked Denoising Autoencoders：Learning Useful Representations in a Deep Network with a Local Denoising Criterion［J］.Journal of Machine Learning Research，2010，11（12）：3371-3408.

［14］ 劉恒，劉振娟，李宏光.基于數據驅動的化工過程參數報警閾值優化［J］.化工學報，2012，63（9）：2733-2738.

［15］ YAN S F，YAN X F.Design teacher and supervised du al stacked auto encoders for quality relevant fault detection in industrial process［J］.Applied Soft Computing，2019，81（1）：105526-105543.

［16］ BATHELT A，RICKER N L，JELALI M.Revision of the Tennessee Eastman Process Model［J］.IFAC Papers "OnLine，2015，48（8）：309-314.

（收稿日期：2024-06-20，修回日期：2024-12-30）

Fault Detection for the Chemical Process Based on LGRSAE Algorithm

YANG Jing chao

（CNOOC Petrochemical Engineering Co.，Ltd.）

Abstract"" Aiming at the conventional linear dimension reducing method’s incapability in extracting local and global structural features of the real complex nonlinear industrial data effectively， a local and global stack retaining auto encoder（LGRSAE）and a process fault detection method based on LGRSAE were developed. In addition， the objective constraints of the locality preserving projection（LPP） algorithm and the principal component analysis（PCA） algorithm were introduced into the objective function of the auto encoder（AE） to extract the features related to the local and global structure of the data， including having LGRAE stacks constructed to form LGRSAE to extract features related to deep local and global structure of the process data. The fault detection results on the TE （Tennessee Eastman） process data set show that， the average fault detection rate of the feature extraction method of LGRSAE is higher than those of the MRSAE and KPCA algorithms and the 1 alarm rate is lower.

Key words"" fault detection， stacked auto encoder， feature extraction， local and global structure preserving， data dimension reduction