混凝土中多點聚集爆炸效應起爆參數優化設計

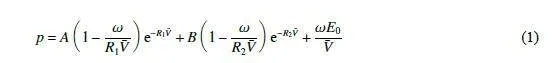
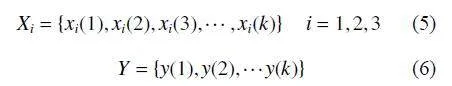
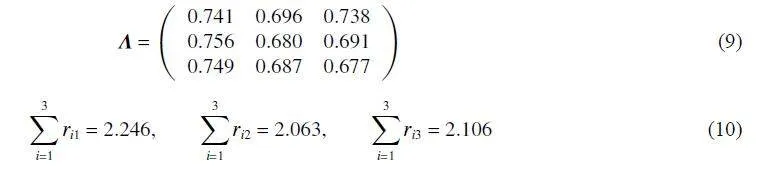
摘要： 混凝土介質中多點同時或彼此微差爆炸可產生復雜的地沖擊波疊加聚集效應，從而使特定作用區域內的地沖擊波壓力顯著增強，大大提升爆炸的毀傷威力。為獲取多點爆源不同排布方式下爆炸聚集效應及地沖擊傳播衰減規律，進行了混凝土中單點和七點聚集爆炸的現場和數值模擬試驗，基于正交設計方法和灰色系統理論對多點起爆參數進行了優化設計，建立了比例裝藥間距、比例有源裝藥高度和比例起爆微差等因素與不同爆心距下峰值壓力間的灰色關聯度系數及灰色關聯度，確定了起爆參數的優選組合，并開展了數值模擬試驗檢驗。分析結果表明：影響地沖擊聚集效應的主要因素為比例裝藥間距，其次為比例起爆微差，最次為比例有源裝藥高度。在本模擬試驗情況下，采用優化的起爆參數時，即在比例裝藥間距為0.549 m/kg1/3、比例起爆微差為0.239 m/kg1/3 和比例有源裝藥高度為0 m/kg1/3時，地沖擊波聚集效應達到最佳，最大可達單點同等裝藥量產生的地沖擊壓力的4.7 倍。

關鍵詞： 灰色理論；聚集爆炸；混凝土；關聯度；優化設計

中圖分類號： O382 國標學科代碼： 1303520 文獻標志碼： A

混凝土中多點爆炸產生的爆炸波聚集效應問題是軍事和民用領域的熱門話題[1-4]。在軍事應用方面，采取多彈同時打擊，可大幅增加鉆地導彈的地沖擊效應，是摧毀高強防護目標的優選方式之一。在民用方面，采用多點同時或彼此微差爆炸方式可在特定范圍形成高壓區，極大提升爆炸有效能量的占比。

由于多點間爆炸波相互作用的復雜性，目前主要采用試驗和仿真手段開展研究工作。文獻[5-6] 對多點同時和微差爆炸的空氣或地面沖擊波做了豐富的理論和試驗探究，結果表明在特定區域內，與單點爆炸比較，多點爆炸產生的峰值壓力是單點爆炸的3～8 倍，可對深地防護工程帶來極大威脅。Hu 等[7]研究了多點不同爆炸陣列對水下爆炸參數的影響，結果表明裝藥數量的增加可以提高沖擊波的高壓區域范圍以及沖量，陣列距離的增大可提高沖量和延長沖擊波作用時間，沖擊波壓力正壓作用時程與裝藥數量、陣列距離密切相關。Izumi 等[8] 通過實驗研究了空氣中不同平面激波強度和不同拋物形壁面深度對反射激波相互作用的影響，結果表明激波馬赫反射所形成的2 個三波點的碰撞是形成激波聚焦的局部高壓區的主要原因，同時，根據反射激波在聚焦前后的形態及其位置關系將激波聚焦分成了3 種模式。除了沖擊波壓力聚集引起的高壓區外，Kishige 等[9] 通過輻射測量實驗證實了氬氣中沖擊波壓力聚集還伴隨著高溫區。Qiu 等[10] 構建了一套同步進行光彈性和焦散方法的同步測量系統，給出了兩點同時爆炸爆炸波的相互作用的光彈和焦散線場圖，存在聚集現象。李旭東等[11] 結合應變儀和高速數字圖像相關方法，探究了三點同時爆炸時爆炸波在水泥板中聚集效應的特性，結果表明，聚集效應將引起正應變在聚集區域強烈的非線性激增，這種猛烈的大變形將對介質和結構帶來顯著的毀壞作用，并且該非線性效應的存在與爆炸點之間的距離有著密切的聯系。Lin 等[12] 對水下多點同步爆炸進行了數值仿真分析，結果表明水下兩點同步爆炸的沖擊波壓力具有非線性疊加效應，約為單點爆炸的1.48～2.52 倍；在總炸藥質量不變的條件下，8 個炸藥同步爆炸對靶體的毀壞作用最嚴重。Kim 等[13] 采用計算流體力學（computational fluid dynamics， CFD） 方法，對弱沖擊波的聚集效應開展了數值分析，從峰值壓力、氣體動力和幾何焦點3 個方面探究了激波的聚焦特性，結果表明激波聚集的峰值壓力及其位置與入射激波馬赫數和反射面幾何形狀有很大關聯性；而氣體動力焦點的位置總是比幾何焦點的位置短，同時隨著入射沖擊波的增強，這種趨勢更加明顯。Liang 等[14] 利用歐拉求解法數值研究了激波聚焦在拋物面反射器上的詳細流場；之后他[15] 又計算了拋物面矢量上的軸對稱沖擊波聚焦現象，得到了不同入射激波馬赫數下不同深度反射器聚集軸對稱激波的復雜流場分布，從計算的流場中可以確定最大壓力發生的位置。Qiu 等[16]利用Overture 數值軟件基于有限差分方法研究了多點爆炸源起爆時沖擊波的相互作用和融合，其目的是通過多點起爆的方式提高特定區域的壓力峰值增大傷害性并大大減小遠離目標區域的附帶傷害。劉玲等[17]通過AUTODYN 仿真軟件研究了商場內部單點爆炸和多點爆炸下爆炸波傳播的特性，研究表明：從人員傷害角度來分析，多點同時起爆較單點爆點的毀傷半徑變大，較單點提高1.41 倍。

綜上所述，目前多點聚集爆炸效應研究多集中于水或空氣介質，關于混凝土等固體介質中多點聚集爆炸效應鮮有深入探討。本文中，在前人研究的基礎上，利用實驗和數值模擬手段對混凝土中多點聚集爆炸效應進行研究，并運用灰色系統理論優化設計起爆參數，以期為提高類似介質中多點爆炸毀傷效能提供原技術參考。

1 混凝土多點聚集爆炸效應數值模擬

1.1 幾何模型

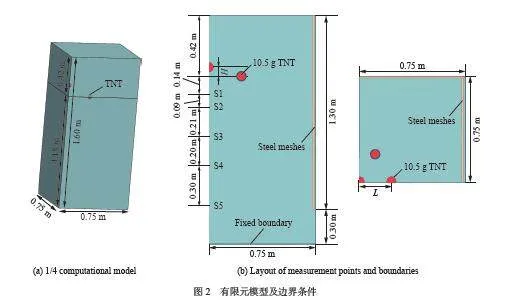
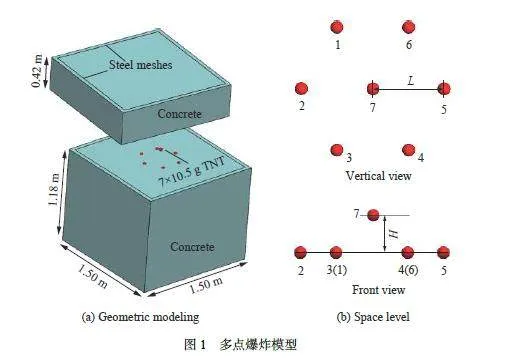
為探究混凝土中七點爆炸對地沖擊聚集效應的影響，建立了圖1（a） 所示的幾何模型。該模型由混凝土、藥球和鋼筋網3 部分組成，其中該模型外形是長方體，長1.5 m，寬1.5 m，高1.6 m。在距混凝土自由面0.42 m 處以正六邊形方式布置7 個藥球，所用藥球的質量均為10.5 g，共73.5 g，起爆點位于藥球球心；鋼筋網安放在靶體邊界，加固靶體。由文獻[18-20] 可知，影響多點聚集爆炸效應的起爆參數主要包括裝藥間距、有源裝藥高度和起爆微差時間；其中，裝藥間距是投影面上7 號藥球的球心到5 號藥球球心的距離L（圖1（b） 上部分）；有源裝藥高度是7 號藥球的球心到周圍1～6 號藥球球心所構成的平面的高度H（圖1（b） 下部分）。為提高7 號藥球產生的爆炸波與1～6 號藥球產生的爆炸波相互作用的同步性，在設置起爆微差時間Ω = L／W1／3時，令7 號藥球起爆時間遲于或等于1～6 號藥球的起爆時間。對以上起爆參數分析各記為：比例裝藥間距為Ω = L／W1／3，Ｗ為7 個藥球的質量之和，本文中選取73.5 g；比例有源裝藥高度為ψ= H／W1／3；比例起爆微差時間Γ= ΔTc／W1／3，c 為混凝土的縱波波速。

1.2 有限元模型

考慮上述幾何模型的對稱性以及降低計算周期，建立了1/4 有限元模型，如圖2（a） 所示。數值模擬時，對靶體和炸藥選用SPH 算法，鋼筋選用beam 算法。如圖2（b） 所示，邊界條件定義為無反射固定邊界，在對稱界面設置對稱約束以限制粒子的旋轉和位移；在裝藥中心正下方設置了S1～S5 監測點，量測爆炸波應力時程曲線。計算單位制采用mm-g-ms。

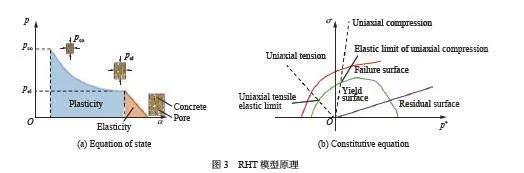
對混凝土選用材料庫中內置的35 MPa 模型[21]，由p-α 狀態方程和RHT（Riedel-Hiermaier-Thoma）本構方程組成，如圖3 所示。采用p-α 狀態方程來表征混凝土等脆性介質在不同受力情況下的力學行為，當壓力小于孔隙破碎壓力pel 時，介質處于彈性狀態；一旦壓力超過pel，孔隙坍塌，引起材料的有效體積模量減小；當壓力達到pco，孔隙被完全壓實，全程是塑性變化。RHT 本構方程中有3 個固定失效面，如圖3（b） 所示。對損傷采用侵蝕算法，將侵蝕因子設置為2.5。對單層鋼筋網選用材料庫中內置的STEEL 模型[21]。

對藥球選用材料庫中炸藥模型[ 2 1 ]。Jones-Wilkins-Lee 方程通常來定義炸藥的爆炸，其具體關系[22] 為：

式中：A、B、R1、R2和ω為特征常數；ˉV=ρ0/ρ，ρ0為初始密度，ρ為密度；E0為初始體積內能。炸藥參數取值如表1[21] 所示，D 為爆轟速度。

1.3 粒子尺寸無關性分析

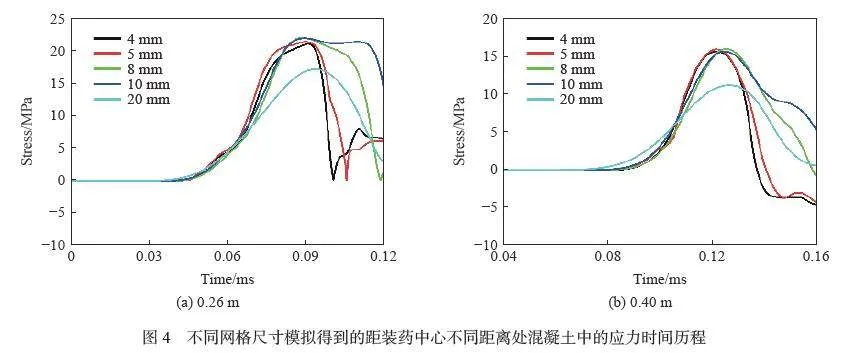
為提高計算精度和求解效率，對計算模型進行粒子無關性分析。為此，分別選用粒子尺寸為4、5、8、10 和20 mm 進行爆炸波傳播的數值模擬。圖4 為距裝藥中心0.26 和0.40 m 處混凝土中的應力時程曲線。

從圖4 可以看出，在粒子尺寸的增大時，爆炸波波峰由陡峭變得平緩，波陣面前的應力由零增大到峰值應力的斜率逐漸降低，爆炸波應力波形逐漸失真。對比圖4 中2 個距離下不同粒子尺寸的沖擊波應力-時程曲線，發現粒子尺寸小于5 mm 的數值模擬是收斂的。因此，選用粒子尺寸為5 mm 進行接下來爆炸波傳播過程的數值模擬。

2 計算模型的試驗驗證

2.1 裝藥設計

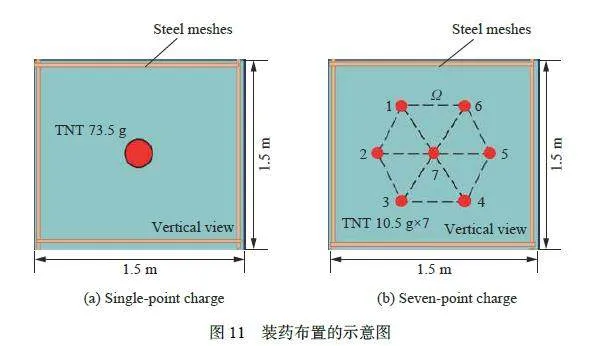
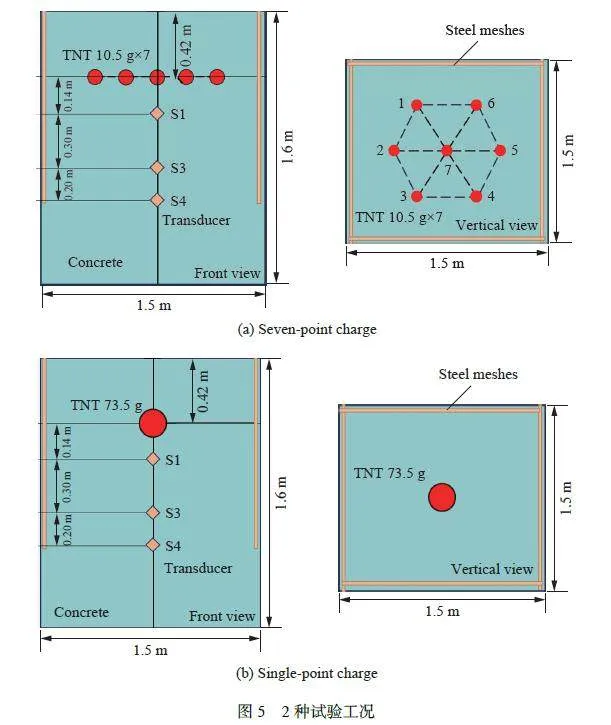
圖5 為混凝土中七點爆炸和單點爆炸的布置圖。第1 組采用七點裝藥：單個藥球質量為10.5 g，藥球的排列輪廓線是邊長為0.23 m 的正六邊形，比例有源裝藥高度為0，裝藥埋深為0.42 m，TNT 藥球總質量為73.5 g，起爆方式采用7 點同時起爆，如圖5（a） 所示。第2 組采用單點裝藥：裝藥質量仍為73.5 g，埋深不變，作為參照組，如圖5（b） 所示。

試驗炸藥均采用球形裝藥，圖6（a） 為試驗中所用藥球的示意圖，裝藥密度為1.5 g/cm3，裝藥上方預留有直徑為8 mm 的雷管安裝孔。該裝藥采用散裝三硝基甲苯（TNT），經一體成型工藝壓裝而成。圖6（b）～（c） 分別為10.5 和73.5 g 藥球，通過雷管起爆。

2.2 靶體設計

采用C35 混凝土澆筑試驗靶體，如圖7 所示。圖中2 個靶體分別是七點裝藥和單點裝藥的試驗靶體，這2 個靶體的尺寸和數值模擬中的幾何模型一致。養護28 d 后，測得C35 混凝土的密度為2 200 kg/m3，抗壓強度為36 MPa。試驗中，采用PVDF 壓電式傳感器獲取不同測點處爆炸波法向應力的時程曲線。電荷放大器選用東華測試公司生產的DH5863A 型號，數據采集選用東華的DH5960 高性能動態信號測試系統，采樣頻率為1 MHz。

2.3 試驗結果與計算模型驗證

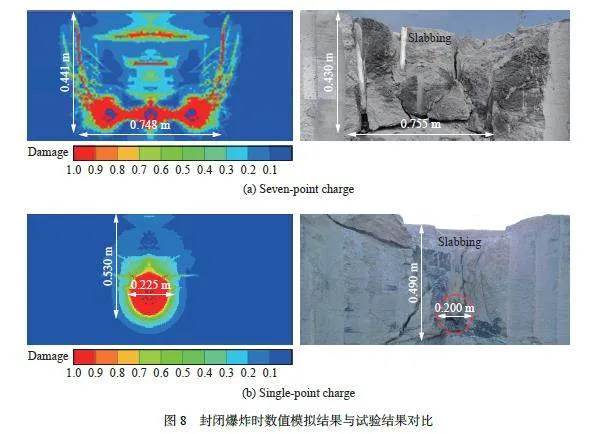
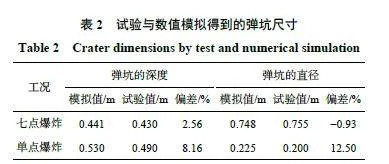
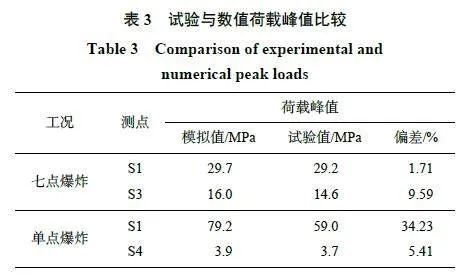
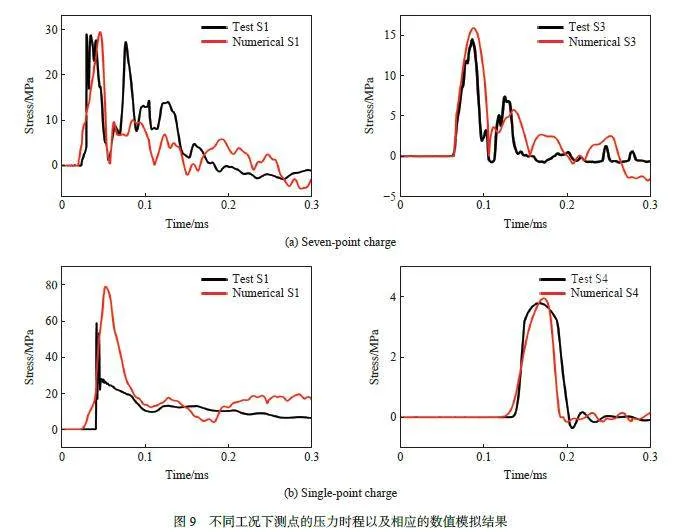
為驗證數值的準確性，分別對2.1 節的2 種試驗工況開展模擬，并互相對比，計算結果如圖8～9 以及表2～3 所示。圖8 中比色卡為混凝土靶體的損傷值，是靶體材料塑性應變的累計，當靶體材料斷裂時，其值為1；可以觀察到，不同裝藥方式下在混凝土頂部表面均有裂紋，但未見有明顯彈坑和拋擲現象，說明2 種裝藥方式下爆破能量基本被封閉。位于七點裝藥所在的平面，各空腔之間相互貫穿，外觀類似餅狀，見圖8（a）；而單點爆炸產生一個獨立空腔，見圖8（b），破壞區域較七點裝藥的小。在試驗現場發現，靶體后表面有明顯的層裂，這是由反射拉伸波造成的。通過對比可知，所使用的數值計算模型可以準確地模擬和反映混凝土靶體的破碎及裂紋擴展情況。試驗和數值模擬得到的混凝土彈坑深度和寬度見表2，最大誤差為12.5 %。圖5 給出了試驗監測點的示意圖，分3 層布設于爆心下方。這2 種試驗工況下各測點的應力時程曲線見圖9，因為部分數據異常，未給出所用的曲線；對比可見，數值模擬的爆炸波峰值應力、升壓時間和正壓持續時間均與實驗數據吻合度較好，經計算其平均偏差約為11.2 %。

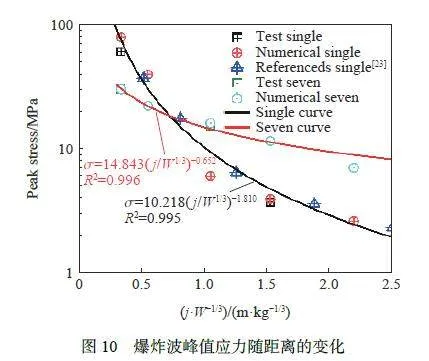
目前一致認為可以利用公式σ=K（j/W1/3）N描述混凝土爆炸波應力衰減規律[23]，其中W 為裝藥質量，單位為kg；j 為爆炸中心到測點的距離，單位為m；K 和N 分別為衰減系數和衰減指數。提取各目標點的峰值應力和比例爆心距離，由上述公式，擬合衰減曲線，如圖10 所示。可知，單點爆炸下衰減指數N 為?1.810，位于Mu 等[23]通過實驗數據確定的不同強度混凝土的衰減系數范圍內（N=?1.84～?1.67），與之吻合較好。多點爆炸下衰減指數N 為?0.652，約為單點爆炸應力波衰減指數的0.36 倍，表明多點爆炸合成的平面應力波衰減速度比單點爆炸產生的球面波要慢，這與平面波可以降低能量耗散速度的事實是一致的。

綜上可知，本文中建立的有限元模型和相關材料模型參數能夠準確地模擬封閉爆炸下單點裝藥和多點裝藥對混凝土靶體的破壞過程和地沖擊傳播的規律。

3 不同比例裝藥間距對爆炸波傳播的影響

同種材料中，取 5 種不同裝藥間距對七點同時爆炸進行數值模擬研究。圖 11 中比例裝藥間距Ω 分別取為0.239、0.406、0.549、0.812 和0.955 m/kg1/3。每種工況的炸藥總質量均為73.5 g，所用藥球的質量和試驗藥球保持一致。

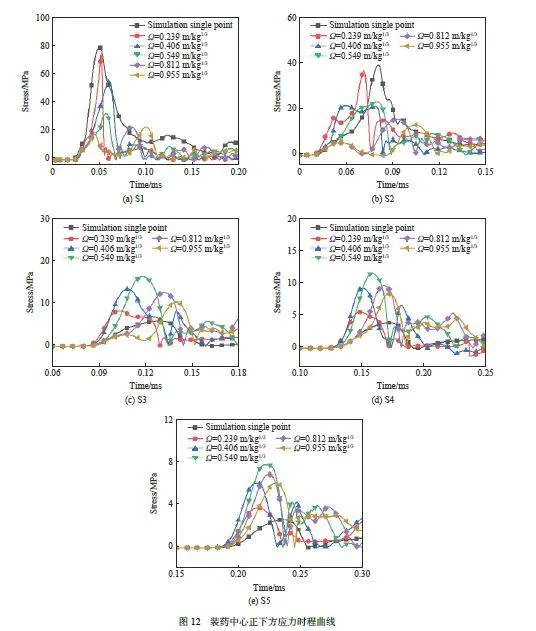
圖12 為裝藥中心下方不同比例裝藥間距下5 個監測點處的應力時程曲線，其中S1、S2、S3、S4、S5 測點位置關系見圖2。另外，圖12（a）～（e） 依此為爆炸波分別在21.7、38.6、82.1、124.3 和184.9 μs 時刻傳播至裝藥中心下方S1、S2、S3、S4 和S5 等5 點處對應的應力時程曲線。由圖12 可知，盡管多點同時爆炸時單個藥球質量在減小，但在S3、S4 和S5 監測點處的峰值應力較單點爆炸時有所增大提高，并且在比例裝藥間距增大的過程中存在一最佳比例裝藥間距，即在比例裝藥間距為0.549 m/kg1/3 時，在各工況中其峰值應力整體最大，在最佳比例裝藥間距下S3、S4 和S5 等3 個觀測點處，峰值應力分別為16、11 和7.8 MPa，較單點爆炸分別提高62.5%、63% 和65.3%；在爆炸近區觀測點S1 和S2 處多點爆炸波的峰值應力是偏低的，這是由于爆炸近區能量過于分散造成。圖13 展示了變裝藥間距下爆炸近區和爆炸遠區的壓力分布云圖。觀察可知，在爆炸近區0.191 m/kg1/3 處，單點裝藥分散成7 個相同質量的藥球時，按5 種裝藥間距進行排布，雖然在裝藥當量相同的條件下壓力作用范圍增大，但爆炸能量空間分布較分散，峰值應力要比單點爆炸的低，且裝藥間距越大峰值應力越低（圖13（a））。當爆炸波傳播至爆心下方比例爆心距1.620 m/kg1/3 處，多點爆炸產生的爆炸波在爆源遠區進行相互疊加合成新類型的波，即各爆源的小球面波疊加變為近平面波傳播，且高壓區面積顯著增大，在比例裝藥間距為0.549 m/kg1/3 時達到最大，如圖13（b） 所示。

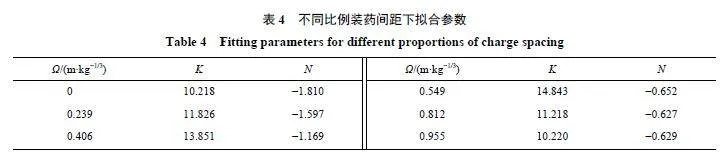
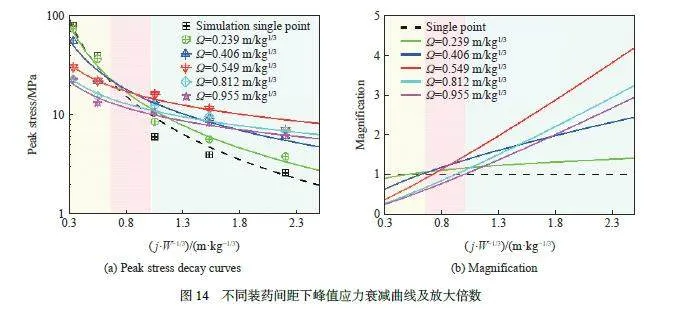
提取圖12 中的峰值應力，由公式σ=K（j/W 1/3）?N 擬合不同比例裝藥間距條件下地沖擊峰值應力，如圖14（a）所示。表4 列出了各工況下的衰減系數K 和衰減指數N 的值；用各間距下的衰減曲線與單點裝藥爆炸衰減曲線進行做比值計算，得到各自的放大倍數變化曲線，如圖14（b） 所示。由圖14 可以看出，藥量73.5 g、比例裝藥間距0.955 m/kg1/3 以內爆炸均可以產生聚集爆炸效應（淺綠色區域）；而且隨著比例裝藥間距的變化，混凝土中爆炸波在衰減特性出現差異性變化，在比例裝藥間距為0.549 m/kg1/3 時，爆炸波衰減速度較其他工況下慢，地沖擊波聚集效應整體表現最佳，且爆炸波傳播的距離越遠這種聚集效應越顯著，如在比例爆心距為2.500 m/kg1/3 處，多點爆炸產生的峰值應力是單點裝藥的4.2 倍。在比例裝藥間距逐漸減小時，地沖擊波聚集效應位置在更高的壓力水平和更淺的深度發生（淺紅色區域）。從表4 可以看出，隨著裝藥間距的增大，衰減指數N 逐漸變小，最終約為單點爆炸衰減指數的1/3，表明爆炸波已從球面波變為近似平面波，爆炸波幾何上的衰減逐漸消失；而衰減系數K 的值隨著比例裝藥間距的增大先增大后減小，在比例裝藥間距為0.549 m/kg1/3 時達到最大。

4 多點聚集爆炸效應優化設計方法

4.1 灰度理論介紹

在系統分析中，定量預測方法多集中于回歸分析模型[24]、時間序列分析[25]、馬爾柯夫鏈模型[26] 和微分方程模型[27]。以上預測方法往往需要較多的樣本數據，且樣本需要滿足典型分布，現實情況下收集較多的數據較困難，通常很難開展下去。而灰色預測模型中的灰色關聯分析法則沒有特殊的條件和限制，通過各因素演變態勢的相近度或相異度來權衡各因素的關聯度。灰色理論現實價值非常大，很好地解決了常用系統分析預測方法難以解決的難題[28-30]。

4.2 無量綱化

在進行灰色理論優化時，由于各因素在量綱上的不同，在求解灰色關聯度前有必要對各因素序列進行無量綱化，具體方法為：

關聯度r0i越大，意味著比較序列Xi與參考序列X0越接近，當r0i = 1時，比較序列與參考序列相同。

4.4 優化效果分析

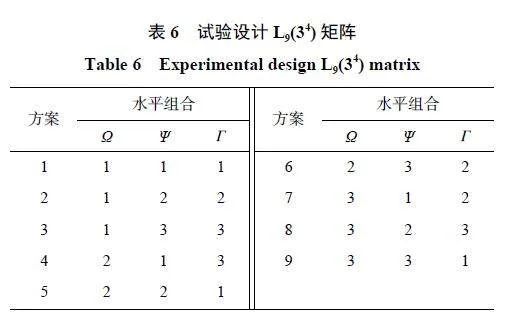
應用灰色理論研究比例裝藥間距 Ω、比例有源裝藥高度 、比例起爆微差時間 對峰值應力的影響。由表5 可知：所研究的問題包含3 個控制因素，分別記為X1、X2、X3，每個控制因素有3 水平。為了提高試驗效率、揭示問題的本質，文中暫不研究參數間的交互作用，采用正交表L9（34）設計試驗，具體設計的試驗工況如表6 所示。

4.4.1 關聯度的計算

將聚集爆炸放大范圍的峰值應力作為參考序列， 由第3 節可知， 比例爆心距為0.962～2.500 m/kg1/3，多點爆炸才有聚集放大效應，即取S3、S4 和S5 監測點的峰值應力作為參考序列，分別記為y1（k）、 y2（k） 和y3（k）。將比例裝藥間距、比例有源裝藥高度和比例起爆微差時間三因素作為比較序列，記為x1（k）、x2（k） 和 x3（k）；將聚集放大區域的S3、S4 和S5 處的峰值應力為參考序列，則比較序列與參考序列的表達式為：

對以上9 種方案進行數值模擬，得到模擬結果序列值為：

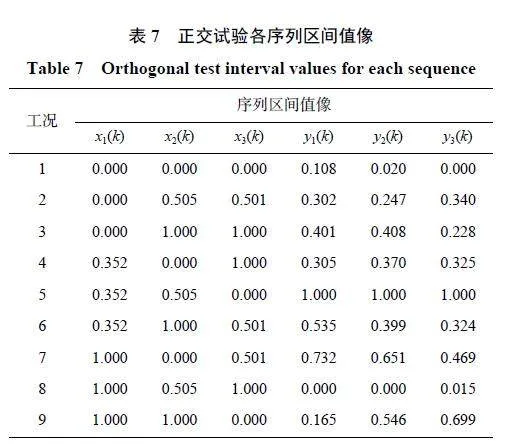
為確保求得的關聯度的準確性，由式（2） 對各序列數值進行量綱歸一化，得各數據序列區間值像，表7 給出了S3、S4 和S5 監測點無量綱化后的結果。

對S3 處峰值應力，由式（3） 得：

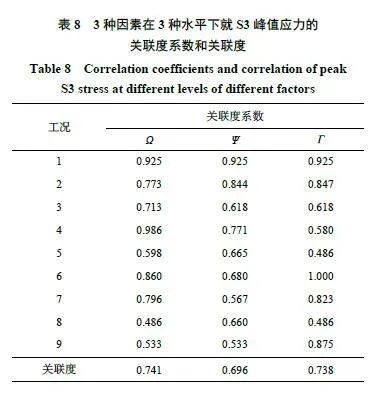
由于εΔ = Δ/Δmax = 0.446/1 = 0.446， 且Δmax≤3Δ，因此1.5εΔ≤ξ≤2εΔ，取ξ= 0.88。同理，求S4 和S5 監測點下分辨系數，均是ξ= 0.8。由式（3） 和式（4） 計算得到了S3 目標下的關聯度系數關聯度，如表8，同理計算S4 和S5 目標下的關聯度系數關聯度。

綜上，求得關聯矩陣：

所以，可知比例裝藥間距 Ω占主要因素，起爆微差時間Γ次之，最后是有源比例裝藥高度ψ。

4.4.2 起爆參數多目標綜合優化

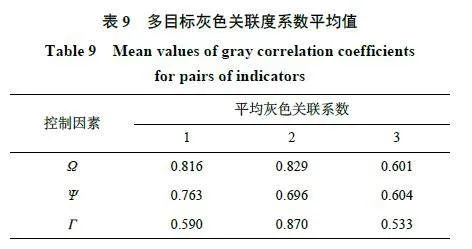
分別計算比例裝藥間距、比例有源裝藥高度、比例起爆微差時間對七點爆炸聚集區峰值應力的灰色關聯度系數均值，得到多目標綜合優化后的平均關聯系數如表9 所示。從表9 可以看出：比例裝藥間距Ω 對多目標綜合優化的灰色關聯序為：r0 （0.549 m/kg1 / 3 ）＞r0 （0.406 m/kg1 / 3 ）＞r0（0.812 m/kg1/3）；比例有源裝藥高度 對多目標綜合優化的灰色關聯序為r0（0）＞r0（0.048 m/kg1/3）＞r0（0.095 m/kg1/3）；比例起爆微差時間 對多目標綜合優化的灰色關聯序為r0 （0.239 m/kg1 / 3 ）＞r0（0）＞r0（0.477 m/kg1/3）。基于以上分析可知混凝土中七點爆炸聚集效應多目標求得一組較佳的組合參數：比例裝藥間距Ω=0.549 m/kg1/3，比例有源裝藥高度Ψ=0 m/kg1 / 3 ，比例起爆微差時間Γ =0.239 m/kg1/3。

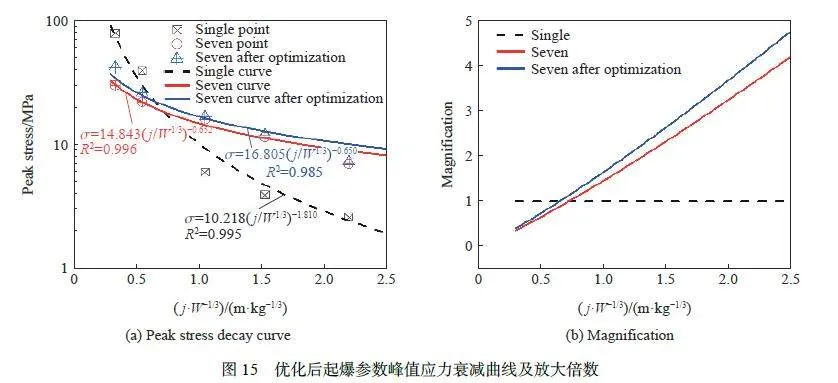
將優化的起爆參數在仿真軟中進行計算，給出了優化設計后應力衰減曲線和放大倍數，如圖15 所示。從圖15 可知：開展多目標優化的起爆參數后，地沖擊波聚集效應得到進一步提高，其中，應力衰減公式中衰減系數K 的值在增大，較單點增加了6.587；同時爆炸壓力在爆心距為2.5 m/kg1/3 處，最大放大倍數由4.2 倍提高到了4.7 倍，表明七點聚集爆炸效應得到了明顯的提高。

5 結 論

對多點裝藥爆炸引起的混凝土內沖擊波衰減進行了實驗和數值模擬工作，研究了裝藥間距對爆炸波的影響，通過正交設計方法和灰色系統理論對多點起爆參數進行優化設計，確定了最優的起爆參數推薦值，主要貢獻和結論如下。

（1）RHT 的混凝土材料模型和SPH 算法可以合理地預測集團和多點裝藥爆炸在不同爆點下的沖擊波傳播以及混凝土的誘導損傷和破壞。

（2） 七點裝藥爆炸引起的混凝土爆炸波傳播規律與單點裝藥爆炸差異較大，且隨著比例裝藥間距的增大，爆炸聚集效應先增強后減弱，在比例裝藥間距為0.549 m/kg1/3 時爆炸聚集效應最佳，在比例爆心距為2.500 m/kg1/3 處，地沖壓力可達同等裝藥量單點裝藥地沖壓力的4.2 倍。

（3） 計算了比例有源裝藥高度0～0.095 m/kg1/3、比例起爆微差時間0～0.477 m/kg1/3 和比例裝藥間距0～0.812 m/kg1/3 條件下的混凝土地沖擊波聚集效應，結合灰色關聯分析法根據仿真結果求解了起爆參數的關聯度系數和關聯度，發現在比例裝藥間距、比例有源裝藥高度、比例起爆微差時間起爆參數中，比例裝藥間距對多點爆炸混凝土中聚集效應影響最為顯著。在本試驗情況下，給出了七點爆炸計算模型的最優起爆參數為比例裝藥間距Ω=0.549 m/kg1/3、比例有源裝藥高度Ψ=0 m/kg1/3、比例起爆微差時間 Γ=0.239 m/kg1/3。

通過對優化設計前后沖擊波壓力放大指標的對比可知，七點聚集爆炸效應得到顯著改善，驗證了優化設計方法的可靠性。這為優化多點起爆參數提供了一種行之有效的方法，豐富了灰色理論的應用價值。

參考文獻：

[1]鄧國強， 周早生， 鄭全平. 鉆地彈爆炸聚集效應研究現狀及展望 [J]. 解放軍理工大學學報（自然科學版）， 2002， 3（3）：45–49. DOI： 10.3969/j.issn.1009-3443.2002.03.012.

DENG G Q， ZHOU Z S， ZHENG Q P. Study status quo and development of aggregated effect of multiple earth penetrator"bursts detonated simultaneously [J]. Journal of the PLA University of Science and Technology， 2002， 3（3）： 45–49. DOI：10.3969/j.issn.1009-3443.2002.03.012.

[2]LENG Z D， SUN J S， LU W B， et al. Mechanism of the in-hole detonation wave interactions in dual initiation with electronic detonators in bench blasting operation [J]. Computers and Geotechnics， 2021， 129： 103873. DOI： 10.1016/j.compgeo.2020.103873.

[3]LENG Z D， FAN Y， GAO Q D， et al. Evaluation and optimization of blasting approaches to reducing oversize boulders and toes"in open-pit mine [J]. International Journal of Mining Science and Technology， 2020， 30（3）： 373–380. DOI： 10.1016/j.ijmst.2020.03.010.

[4]GAO Q D， LU W B， YAN P， et al. Effect of initiation location on distribution and utilization of explosion energy during rock"blasting [J]. Bulletin of Engineering Geology and the Environment， 2019， 78（5）： 3433–3447. DOI： 10.1007/s10064-018-1296-4.

[5]PHILLIPS J S， BRATTON J L. ground shock analysis of the multiple burst experiments： ADA 088510 [R]. Springfield： NITS，1978.

[6]RUETENIK J R， HOBBS N P， SMILEY R F. Calculation of multiple burst interactions for six simultaneous explosions of 120"Ton ANFO charges： ADA 091978 [R]. Springfield： NITS， 1979.

[7]HU H W， SONG P， GUO S F， et al. Shock wave and bubble characteristics of underwater array explosion of charges [J].Defence Technology， 2022， 18（8）： 1445–1453. DOI： 10.1016/J.DT.2021.05.020.

[8]IZUMI K， ASO S， NISHIDA M. Experimental and computational studies focusing processes of shock waves reflected from"parabolic reflectors [J]. Shock Waves， 1994， 3（3）： 213–222. DOI： 10.1007/BF01414715.

[9]KISHIGE H， TESHIMA K， NISHIDA M. Focusing of shock waves reflected from an axisymmetrically parabolic wall [C].Proceedings of the 18th International Symposium on Shock Waves. Sendai： Springer， 1992： 341–345. DOI： 10.1007/978-3-642-77648-9_50.

[10]QIU P， YUE Z W， ZHANG S C， et al. An in situ simultaneous measurement system combining photoelasticity and caustics"methods for blast-induced dynamic fracture [J]. Review of Scientific Instruments， 2017， 88（11）： 115113. DOI： 10.1063/1.4994811.

[11]李旭東， 劉凱欣， 張光升， 等. 沖擊波在水泥砂漿板中的聚集效應 [J]. 清華大學學報（自然科學版）， 2008， 48（8）：1272–1275. DOI： 10.16511/j.cnki.qhdxxb.2008.08.004.

LI X D， LIU K X， ZHANG G S， et al. Focusing of shock waves in cement mortar plates [J]. Journal of Tsinghua University"（Science amp; Technology）， 2008， 48（8）： 1272–1275. DOI： 10.16511/j.cnki.qhdxxb.2008.08.004.

[12]LIN S J， WANG J X， LIU L T， et al. Research on damage effect of underwater multipoint synchronous explosion shock waves"on air-backed clamped circular plate [J]. Ocean Engineering， 2021， 240： 109985. DOI： 10.1016/j.oceaneng.2021.109985.

[13]KIM H D， KWEON Y H， SETOGUCHI T， et al. A study on the focusing phenomenon of a weak shock wave [J]. Proceedings"of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2003， 217（11）： 1209–1220.DOI： 10.1243/095440603771665241.

[14]LIANG S M， TSAI C J， WU L N. Efficient， robust second-order total variation diminishing scheme [J]. AIAA Journal， 1996，34（1）： 193–195. DOI： 10.2514/3.13042.

[15]LIANG S M， WU L N， HSU R L. Numerical investigation of axisymmetric shock wave focusing over paraboloidal"reflectors [J]. Shock Waves， 1999， 9（6）： 367–379. DOI： 10.1007/S001930050167.

[16]QIU S， ELIASSON V. Interaction and coalescence of multiple simultaneous and non-simultaneous blast waves [J]. Shock"Waves， 2016， 26（3）： 287–297. DOI： 10.1007/s00193-015-0567-2.

[17]劉玲， 袁俊明， 劉玉存， 等. 大型商場多點爆炸恐怖襲擊事故數值模擬 [C]//中國化學會第29 屆學術年會摘要集： 第29 分會： 公共安全化學. 北京： 中國化學會， 2014.

[18]鄧國強， 龍汗， 周早生， 等. [18] 鉆地彈砂土中聚集爆炸地沖擊試驗與預測 [J]. 防護工程， 2001， 23（3）： 24–28.

[19]葉海旺， 石文杰， 王二猛， 等. 金堆城露天礦生產爆破合理微差時間的探討 [J]. 爆破， 2010， 27（1）： 96–98. DOI： 10.3963/j.issn.1001-487X.2010.01.026.

YE H W， SHI W J， WANG E M， et al. Research of reasonable delay intervals in Jinduicheng open-pit mine [J]. Blasting，2010， 27（1）： 96–98. DOI： 10.3963/j.issn.1001-487X.2010.01.026.

[20]顧強， 張世豪， 安曉紅， 等. 基于灰色理論的兩點爆炸起爆參數優化設計 [J]. 爆炸與沖擊， 2015， 35（3）： 359–365. DOI：10.11883/1001-1455（2015）03-0359-07.

GU Q， ZHANG S H， AN X H， et al. Optimization design for priming parameters of two-point explosion based on gray"theory [J]. Explosion and Shock Waves， 2015， 35（3）： 359–365. DOI： 10.11883/1001-1455（2015）03-0359-07.

[21]Century Dynamics Inc. Ansys/Autodyn Version 11.0： user documentation [Z]. Pennsylvania， USA： Century Dynamics Inc.，2007： 89–112.

[22]LEE E L， TARVER C M. Phenomenological model of shock initiation in heterogeneous explosives [J]. The Physics of Fluids，1980， 23（12）： 2362–2372. DOI： 10.1063/1.862940.

[23]MU C M， ZHOU H， MA H F. Prediction method for ground shock parameters of explosion in concrete [J]. Construction and"Building Materials， 2021， 291： 123372. DOI： 10.1016/J.CONBUILDMAT.2021.123372.

[24]OSEI F B， DUKER A A， STEIN A. Bayesian structured additive regression modeling of epidemic data： application to"cholera [J]. BMC Medical Research Methodology， 2012， 12（1）： 118. DOI： 10.1186/1471-2288-12-118.

[25]LI F G， LUAN P X. ARMA model for predicting the number of new outbreaks of Newcastle disease during the month [C]. //2011 IEEE International Conference on Computer Science and Automation Engineering. Shanghai， China： IEEE， 2011： 660–663. DOI： 10.1109/CSAE.2011.5952933.

[26]KOROSTIL I A， PETERS G W， CORNEBISE J， et al. Adaptive Markov chain Monte Carlo forward projection for statistical"analysis in epidemic modelling of human papillomavirus [J]. Statistics in Medicine， 2013， 32（11）： 1917–1953. DOI： 10.1002/sim.5590.

[27]ROBERTS M G， LAWSON J R， GEMMELL M A. Population dynamics in echinococcosis and cysticercosis： mathematical"model of the life-cycles of Taenia hydatigena and T. ovis [J]. Parasitology， 1987， 94（1）： 181–197. DOI： 10.1017/S0031182000053555.

[28]HUANG J C. Application of grey system theory in telecare [J]. Computers in Biology and Medicine， 2011， 41（5）： 302–306.DOI： 10.1016/j.compbiomed.2011.03.007.

[29]LEE Y S， TONG L I. Forecasting energy consumption using a grey model improved by incorporating genetic programming [J].Energy Conversion and Management， 2011， 52（1）： 147–152. DOI： 10.1016/j.enconman.2010.06.053.

[30]王瑩， 肖巍， 姚熊亮， 等. 水下爆炸沖擊波載荷作用下冰層破碎特性及其影響因素 [J]. 爆炸與沖擊， 2019， 39（7）： 073103.DOI： 10.11883/bzycj-2018-0141.

WANG Y， XIAO W， YAO X L， et al. Fragmentation of ice cover subjected to underwater explosion shock wave load and its"influence factors [J]. Explosion and Shock Waves， 2019， 39（7）： 073103. DOI： 10.11883/bzycj-2018-0141.

[31]呂鋒. 灰色系統關聯度之分辨系數的研究 [J]. 系統工程理論與實踐， 1997， 17（6）： 49–54. DOI： 10.3321/j.issn：1000-6788.1997.06.011.

Lü F. Research on the identification coefficient of relational grade for grey system [J]. Systems Engineering： Theory amp;Practice， 1997， 17（6）： 49–54. DOI： 10.3321/j.issn：1000-6788.1997.06.011.

（責任編輯 張凌云）

基金項目： 國家自然科學基金（52279120，12072371）；江蘇省自然科學基金（BK20221528）；爆炸沖擊防災減災全國重點實驗室基金（LGD-SKL-202202）