靈活運(yùn)用冪的運(yùn)算法則

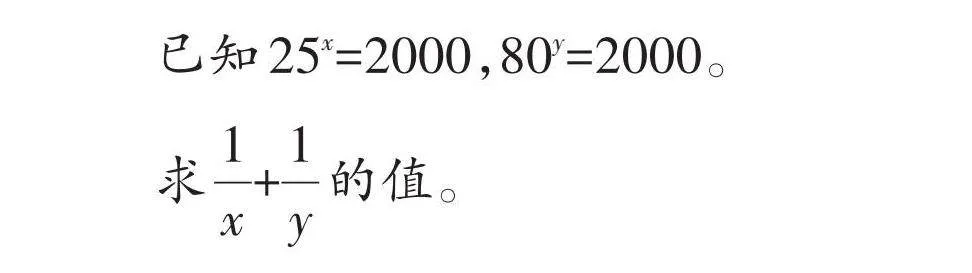
近期，我們?cè)趯W(xué)習(xí)有理數(shù)運(yùn)算的基礎(chǔ)上，進(jìn)一步學(xué)習(xí)了冪的運(yùn)算，包括同底數(shù)冪的乘法、冪的乘方與積的乘方、同底數(shù)冪的除法等，相應(yīng)的運(yùn)算法則分別為：

am?an=am+n（m、n是整數(shù)）；

（am）n=amn（m、n是整數(shù)）；

（ab）m=ambm（m是整數(shù)）；

am÷an=am-n（a≠0，m、n是整數(shù)）。

根據(jù)冪的意義，記住這些運(yùn)算法則并不難，但怎樣靈活運(yùn)用這些運(yùn)算法則解決具體的問(wèn)題是有難度的。比如我遇到的這道題：

已知25x=2000，80y=2000。

求[1x]+[1y]的值。

初看這道題，面對(duì)如此龐大的數(shù)字，采用乘方運(yùn)算或開(kāi)方運(yùn)算都行不通，我感覺(jué)無(wú)從下手。進(jìn)一步觀察條件，我發(fā)現(xiàn)解決問(wèn)題的關(guān)鍵隱含在底數(shù)25和80這兩個(gè)數(shù)字上，依據(jù)是25與80的積恰好為2000。根據(jù)這個(gè)突破口，我先將這兩個(gè)等式的左右兩邊分別相乘，得到25x×80y=4000000。這時(shí)，我又發(fā)現(xiàn)等式左邊兩個(gè)因數(shù)的底數(shù)和指數(shù)都不相同。于是，我針對(duì)這個(gè)特征進(jìn)行了相應(yīng)的處理。

【處理方法1】我嘗試將指數(shù)統(tǒng)一。

因?yàn)?5x=2000，80y=2000，所以（25x）y=2000y，（80y）x=2000x。

于是，可得（25x）y×（80y）x=2000y×2000x。

因?yàn)椋?5x）y×（80y）x=（25×80）xy=2000xy，2000y×2000x=2000x+y，

所以2000xy=2000x+y，即xy=x+y。

因?yàn)閇1x]+[1y]=[x+yxy]，

所以[1x]+[1y]=[x+yxy]=1，

即[1x]+[1y]=1。

這樣，我用（am）n=amn和am?an=am+n輕松地做到冪的指數(shù)的統(tǒng)一，從而解決問(wèn)題。

再次觀察題目給出的條件，我發(fā)現(xiàn)從條件中可以直接湊出代數(shù)式[1x]+[1y]，隨后做如下處理。

【處理方法2】我嘗試將底數(shù)統(tǒng)一。

因?yàn)?5x=2000，80y=2000，所以（25x）[1x]=2000[1x]=25，（80y）[1y]=2000[1y]=80。由此可得2000[1x]×2000[1y]=25×80。所以2000[1x+1y]=2000，即[1x]+[1y]=1。

通過(guò)上面兩種處理方法的嘗試，我發(fā)現(xiàn)，只要靈活運(yùn)用那些基礎(chǔ)公式，就能巧妙地解決一些看似復(fù)雜的難題。這樣的經(jīng)歷讓我對(duì)這些法則的運(yùn)用更加自信，以后在學(xué)習(xí)中遇到類(lèi)似的問(wèn)題，我相信自己能夠更加熟練地應(yīng)對(duì)。

教師點(diǎn)評(píng)

“冪的運(yùn)算”中蘊(yùn)含大量的計(jì)算問(wèn)題，同學(xué)們根據(jù)冪的運(yùn)算法則能熟練解決很多冪的運(yùn)算問(wèn)題。管君豪同學(xué)列舉的問(wèn)題，已知條件與待求結(jié)論之間沒(méi)有明顯的聯(lián)系，具有一定的挑戰(zhàn)性。他在理解冪的運(yùn)算法則的基礎(chǔ)上，靈活運(yùn)用，分別采用了“指數(shù)統(tǒng)一”和“底數(shù)統(tǒng)一”兩種處理方法，巧妙地解決了問(wèn)題，使我們感受到數(shù)學(xué)思想的價(jià)值和魅力。

（指導(dǎo)教師：孫凱）