基于改進灰狼優化算法的區間二型TSK FLS方法在化工過程軟測量中的應用

摘 要 針對具有強非線性、復雜性的化工過程軟測量建模問題，在區間二型TSK模糊系統（IT2 TSK FLS）的基礎上，結合改進灰狼優化（IGWO）算法策略，提出IGWO IT2 TSK FLS方法。與一型TSK模糊邏輯系統方法相比，IT2 TSK FLS方法可以同時建模個體內不確定性和個體間的不確定性，在現有誤差反向傳播（BP）算法訓練的基礎上，將IGWO算法用于模型前件參數和后件參數的設計，以進一步提高模型的預測性能。通過對灰狼優化算法進行改進，引入早熟收斂判斷機制、非線性余弦調整策略、Levy飛行策略，提高算法的收斂速度并避免陷入局部最優。將IGWO IT2 TSK FLS方法應用于脫丁烷塔的軟測量實例建模中，在同等條件下，對一型TSK FLS方法以及BP算法、遺傳算法（GA）、差分進化（DE）、粒子群優化（PSO）、生物地理學優化（BBO）、灰狼優化算法（GWO）等優化的IT2 TSK FLS方法進行比較，實驗結果表明：IGWO IT2 TSK FLS方法在性能上優于對比方法，證實了方法的有效性和應用潛力。

關鍵詞 IGWO IT2 TSK FLS方法 脫丁烷塔 軟測量建模 早熟收斂判斷機制 非線性余弦調整策略

Levy飛行策略

中圖分類號 TP183"" 文獻標志碼 A"" 文章編號 1000 3932（2025）01 0083 11

在化工生產中，針對難以直接測量的關鍵質量變量，常采用分析儀器或離線化驗方法測定，然而儀器成本高、檢驗時間長且無法進行實時監測［1］，為此，基于數據驅動的軟測量方法應運而生，通過挖掘易測變量與關鍵質量變量間的潛在聯系，構建模型，實現對關鍵變量的間接快速測量。軟測量的發展給提高關鍵質量變量的實時監測效率提供了新途徑，同時弱化了對離線化驗的依賴，降低了硬件儀器設備的投入成本［2］。軟測量方法主要可劃分為機理驅動建模、數據驅動建模和兩者結合的混合模型［3］。機理驅動建模雖然具有物理意義直觀和預測精度高的優點，但在實際應用中（特別是化工過程）難以獲得機理知識［4］。相較而言，基于數據驅動的建模方法更關注輸入輸出數據間的聯系［5］，因此在化工過程軟測量領域備受關注［6，7］。

近年來，支持向量機（Support Vector Machines，SVM）［8，9］、神經網絡［10］等人工智能方法已廣泛應用于基于數據驅動的化工過程建模中，其優勢是能夠從歷史數據中描述出易測過程變量與難以直接測量的主導變量間的非線性映射規律，更適用于化工過程主導變量的非線性特性分析。由IF THEN規則刻畫的模糊邏輯系統（Fuzzy Logic Systems，FLS）作為一種強有力的人工智能方法，在化工過程軟測量領域也具有很好的應用潛力，文獻［11］采用遺傳算法（Genetic Algorithm，GA）優化一型TSK FLS參數，成功應用于某污水處理實時監測系統中；文獻［12］采用GA算法優化一型TSK FLS參數，應用于煤氣爐預測，預測效果顯著。區間二型TSK FLS由LIANG Q L和MENDEL J M［13］提出，與傳統一型TSK FLS相比，該方法能夠更有效地處理建模不確定性問題，作為一種強有力的建模工具，已被成功應用于系統辨識與建模控制［14，15］。文獻［16］將區間二型FLS方法應用于工業熱軋帶表面溫度預測，通過反向傳播算法（Back Propagation，BP）來調節模型參數，取得了滿意的預測效果。相應地，智能優化算法也被成功應用于區間二型TSK FLS模型的參數優化中，文獻［17］將GA優化算法應用于區間二型TSK FLS參數設計中，成功應用于工業焦爐液位預測，取得了較好的預測效果；文獻［18］基于粒子群優化（Particle Swarm Optimization，PSO）算法訓練區間二型TSK FLS參數，成功應用于燃氣輪機故障診斷。灰狼優化算法（Grey Wolf Optimizer，GWO）［19］通過模擬灰狼種群的等級制度和狩獵行為，實現了多目標最優化求解，具有效率高、控制參數少等優勢。文獻［20］基于GWO算法優化多層感知器，并在5個分類和3個函數逼近數據集上進行測試，相較于GA算法、差分進化（DE）和PSO算法，GWO具有更好的優化性能；文獻［21］將GWO算法應用于一型TSK FLS控制器的參數設計中，成功應用于太陽能跟蹤系統，控制效果良好。但傳統GWO算法存在線性收斂因子不能有效均衡全局探索和局部搜索的過程，存在尋優能力不強、易因早熟現象而陷入局部極值問題［22，23］。為此，筆者提出一種改進的灰狼優化算法（Improved Gray Wolf Optimizer，IGWO），通過引入早熟收斂判斷機制，判別算法是否陷入局部極值；引入Levy飛行策略，提高種群多樣性，從而使算法跳出局部極值；在灰狼位置更新時引入非線性收斂因子，以滿足不同時期的尋優要求，進而提高算法的收斂速度。在文獻［21］的基礎上，鑒于優化算法在區間二型TSK FLS方法上的成功應用，筆者將GWO算法應用于區間二型TSK FLS方法的優化設計，再進一步將設計的IGWO算法應用于區間二型TSK FLS方法的優化設計中，并在同等算例同等條件下，與一型TSK FLS、區間二型TSK FLS，基于GA算法、DE算法、PSO算法、生物地理學優化算法（Biogeography based Optimization，BBO）優化的區間二型TSK FLS進行比較，驗證筆者方法的性能。

1 區間二型TSK FLS

區間二型TSK FLS（Interval Type 2 Takagi Sugeno Kang Fuzzy Logic Systems，IT2 TSK FLS）分為3種類型：A2 C1、A2 C0、A1 C1，其中，A、C分別為前件和后件的簡寫，如IT2 TSK FLS A2 C1的前件是二型模糊集，后件是區間一型模糊集的二型模糊系統。

假設給定一系列N個輸入-輸出數據對：

（x（1）：y（1）），…，（x（N）：y（N））=｛x，x，…，x：y｝

其中，x∈X，…，x∈X為模型輸入；y∈Y為輸出。

可設計具有M條規則的IT2 TSK FLS，其每條規則具有p個前件，其中第i條規則可描述為：

其中，C（j=0，1，…，p）是后件一型模糊集，第i條規則的輸出為一型模糊集的線性組合，同樣為一型模糊集，C=［c-s，c+s］，c表示模糊集C的中心，s表示模糊集C的伸展度； 是與x（t）相對應的前件區間二型模糊集。

這類規則同時考慮到前件隸屬度函數和后件參數的不確定性。規則中的 由具有不確定均值的第k個先驗高斯型主隸屬函數描述：

μ（x）=exp-，k=1，2，…，p∈［，］，（x）∈［（x），（x）］" （2）

其中，（x）、（x）分別為上、下隸屬函數；為第k類變量的均值集合；m為第k類變量的均值；、、簡記為m、m、σ，即有：

（x）=N（m，σ；x），xlt;m1"""""nbsp; ，m≤x≤mN（m，σ；x），xgt;m """ （3）

（x）=N（m，σ；x），x≥N（m，σ；x），xlt;"""" （4）

N（m，σ；x）=exp［-（（x-m）/σ）2］

定理1［24］ 在以乘積或最小t-范進行交運算的IT2 TSK FLS中，（a）規則Ri的點火集F i（x）是一個區間一型集，即：

F i（x）=［" i（x）， i（x）］"""" " （5）

i（x）=（x）∩…∩（x）

i（x） = （x）∩…∩ （x）

（b）規則Ri的后件Yi也是一個區間一型集，即Yi=［y，y］，其中：

y=cx+c-xs-s

y=cx+c+xs+s

相應地，IT2 TSK FLS的輸出可簡化為：

其中， i， i，y，y由式（6）、（7）計算得到。因此Y（x）是一個區間一型集，為求解Y（x），通常對y和y的平均值進行解模糊化，任何IT2 TSK FLS解模糊化輸出都為：

Y（x）="""""" （9）

若考慮后件為一個清晰Ri數，即零型集的特殊情況，此時即為IT2 TSK FLS A2 C0，則式（1）的規則Ri可描述為：

定理1的（a）仍然適用，（b）則不適用，式（8）簡化為：

Y（x）=［y，y］="" （11）

式（11）中，除了y=y=yi之外，其他計算yl和yr的步驟與A2 C1型 TSK FLS的情形相同。

若考慮后件集是一型模糊集，前件同樣是一型模糊集的特殊情況，記為IT2 TSK FLS A1 C1，則式（1）中的規則Ri可描述為：

此時定理1仍然適用，第i條規則的點火集是一個清晰數，式（8）則可簡化為：

Y=，"""" （13）

由式（8）、（13）的解模糊化輸出為：

Y（x）="""" （14）

若考慮后件集是一個清晰數，前件是一型模糊集的特殊情況，即為一型TSK FLS A1 C0，則式（1）中的規則Ri可描述為：

解模糊化輸出為：

Y（x）="" （16）

2 IT2 TSK FLS的IGWO算法設計

由于BP算法容易陷入局部極小，會在一定程度上影響模型的預測性能。為此，筆者嘗試用IGWO算法對前、后件參數進行優化，替代BP算法完成訓練設計過程，訓練結束后，參數凍結，模型構建完畢。預測時，依據測試數據，輸入所構建的預測模型得到輸出，實現預測目標。

GWO算法具有總體結構簡單、易于編程、收斂速度快、搜索效率高等特點，目前已在多峰函數優化、參數估計、優化調度等領域應用。但傳統GWO算法在進化后期因種群多樣性迅速下降而經常遇到早熟和局部收斂問題，限制了其在工程優化領域的進一步應用。為此，筆者通過引入早熟收斂判斷機制、Levy飛行策略和收斂因子非線性調整策略3種改進策略，構造出一種具有全局尋優性能的改進灰狼優化算法（IGWO），以期為解決IT2 TSK FLS模型參數優化提供有力工具。

2.1 GWO算法

GWO算法通過模擬灰狼的社會結構和群體狩獵方式求解優化問題。算法依據適應度值將種群中的灰狼個體劃分為4個等級（圖1），適應度值最優的3個灰狼個體依次記為α、β和δ，其余為ω。由α、β和δ引導種群其余個體，向獵物位置（全局最優解）逼近，完成狩獵。

灰狼狩獵的數學模型為：

D=C·X（t）-X（t）X（t+1）=Xp（t）-A·D"""" （17）

"""""""" A=2a·r-a"""""" （18）

"""""""" C=2·r""""""" （19）

"""""""" a=2（1-t/T）"""""" （20）

其中，A和C是協同系數向量；X（t）是獵物位置向量；X（t）為灰狼所處位置；D為灰狼與獵物間的距離向量；t是當前迭代次數；T為最大迭代次數；a為收斂因子；r、r為［0，1］之間的隨機向量。

灰狼狩獵的位置更新公式為：

X=X-A·｜C·X-X｜X=X-A·｜C·X-X｜X=X-A·｜C·X-X｜" """（21）

X（t+1）=""""""" """ （22）

其中，X、X、X分別代表α、β、δ的位置向量；X、X、X分別表示狼群中ω向α、β、δ移動的方向向量；X（t+1）定義了最終位置，即表示其余灰狼ω向獵物移動的方向向量。

2.2 改進灰狼優化算法

2.2.1 早熟收斂判斷機制

GWO算法具有不過分依賴參數設置等優點，但在解決復雜優化問題時，容易過早陷入局部極值，即早熟收斂現象。為此，引入早熟收斂判斷機制，將種群的群體適應度方差σ2作為衡量種群所有個體聚集程度的評價標準，表達式為［25］：

σ2="""" （23）

f=f" """" （24）

f=max{｜f-f｜}，max{｜f-f｜}gt;11"""" ，其他"" （25）

其中，f為歸一化定標因子，起到限制σ2大小的作用；S為種群規模；f為第i個灰狼的適應度值；f為種群的平均適應度值。

由式（23）可以看出，σ2越小，種群個體的聚集程度越高，這種聚集將導致種群失去多樣性，致使算法陷入局部最優。因此，當σ2lt;c（c為一常數）時需進行早熟處理，以避免早熟缺陷。

2.2.2 Levy飛行策略

為解決算法早熟造成的局部最優解問題，引入Levy飛行［26］策略增加灰狼種群的多樣性，從而獲得全局最優解。由早熟判斷機制評估種群個體的聚集程度，若滿足早熟條件則進行早熟處理（即引入Levy飛行對灰狼個體執行隨機搜索）。

Levy飛行的隨機步長Levy（ξ）可表示為［27］：

Levy（ξ）=，ξ=1.5""" " （26）

其中，μ、v為方向向量，服從正態分布，即μ～N（0，σ）v～N（0，σ），σ=σ=1。

算法若滿足早熟判斷條件，則用下式替換式（21），改進灰狼狩獵的位置更新公式為：

X′=X+λ·Levy（ξ）X′=X+λ·Levy（ξ） X′=X+λ·Levy（ξ）"""" （27）

λ=0.01×（X-X）λ=0.01×（X-X） λ=0.01×（X-X）" """"""" """""（28）

X（t+1）="""" （29）

其中，λ是步長信息，用于控制Levy飛行隨機搜索范圍。

2.2.3 改進非線性收斂因子策略

由前述可知，傳統GWO算法中收斂因子a隨迭代次數的增加而線性遞減，而這種更新機制不能有效均衡全局探索和局部搜索的過程，不利于增強算法的全局尋優能力。為此，引入一種非線性余弦收斂因子a，即：

a=×cos+1 """""（30）

其中，a為收斂因子a的初始值。

在式（30）的非線性余弦調整策略中，a前期下降緩慢，有利于增強算法的全局探索能力，后期下降加快，能有效提高算法的收斂性。

2.3 IGWO IT2 TSK FLS方法

為了把IGWO優化算法應用于IT2 TSK FLS方法的參數訓練中，將灰狼個體的位置X與IT2 TSK FLS模型的待優化參數相關聯。針對A2 C1、A2 C0、A1 C1這3種不同的IT2 TSK FLS，待優化前件與后件參數具體如下：

在IGWO優化TSK FLS方法實現過程中，將最大化適應度函數J（X），即：

J（X）=""""""" （34）

E="""" （35）

其中，E為均方根誤差；y（i）為模型的預測輸出；y（i）是實際值；N為訓練集樣本數。

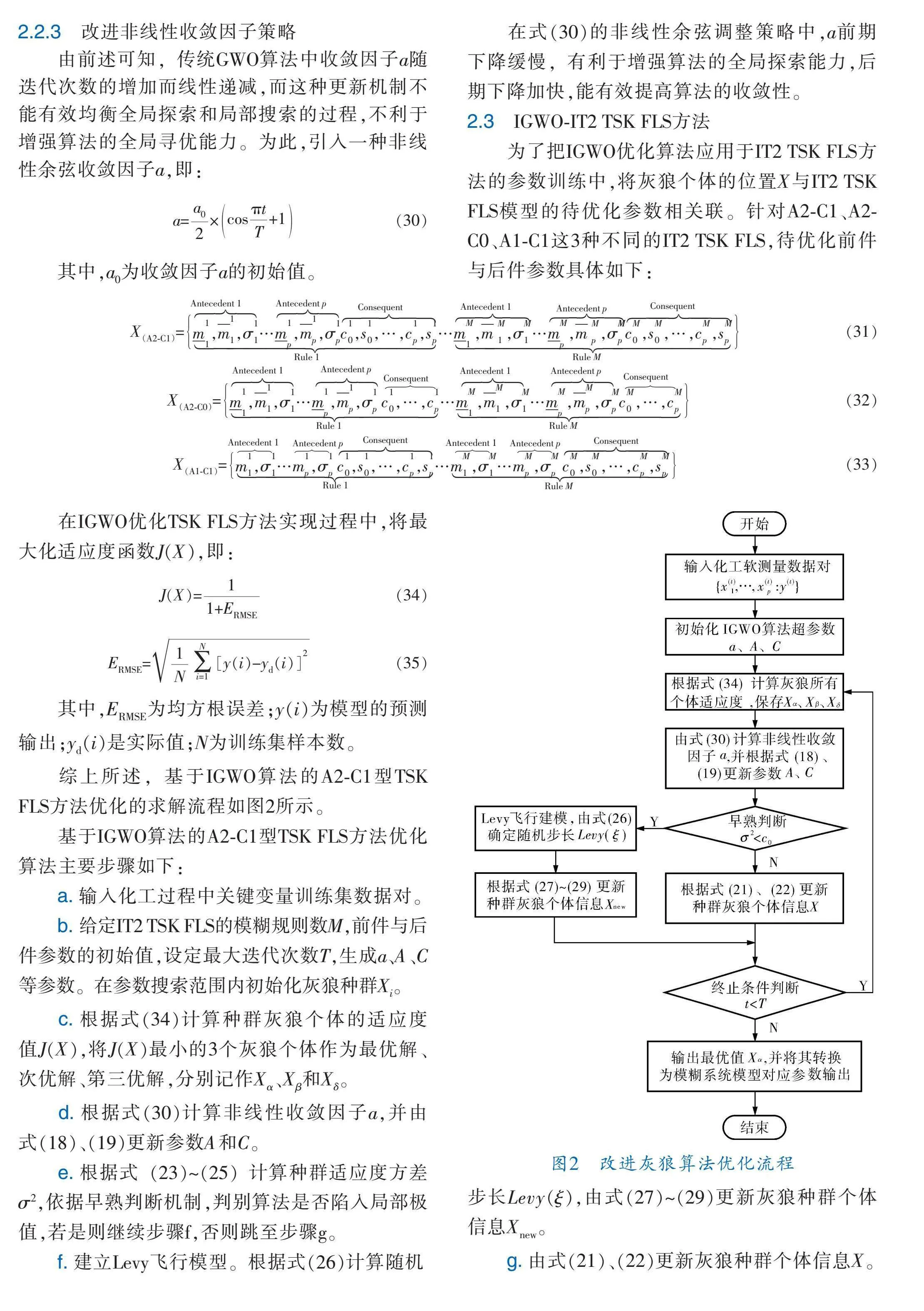
綜上所述，基于IGWO算法的A2 C1型TSK FLS方法優化的求解流程如圖2所示。

基于IGWO算法的A2 C1型TSK FLS方法優化算法主要步驟如下：

a. 輸入化工過程中關鍵變量訓練集數據對。

b. 給定IT2 TSK FLS的模糊規則數M，前件與后件參數的初始值，設定最大迭代次數T，生成a、A、C等參數。在參數搜索范圍內初始化灰狼種群X。

c. 根據式（34）計算種群灰狼個體的適應度值J（X），將J（X）最小的3個灰狼個體作為最優解、次優解、第三優解，分別記作X、X和X。

d. 根據式（30）計算非線性收斂因子a，并由式（18）、（19）更新參數A和C。

e. 根據式（23）～（25）計算種群適應度方差σ2，依據早熟判斷機制，判別算法是否陷入局部極值，若是則繼續步驟f，否則跳至步驟g。

f. 建立Levy飛行模型。根據式（26）計算隨機步長Levy（ξ），由式（27）～（29）更新灰狼種群個體信息X。

g. 由式（21）、（22）更新灰狼種群個體信息X。

h. 根據式（34）更新所有灰狼個體的適應度值J（X），以此為依據更新X、X和X。

i. t=t+1，若tlt;T，跳轉到步驟c，否則終止算法，輸出最優解X，并依據式（31）將其轉換為A2 C1型TSK FLS模型的參數輸出。

3 應用算例

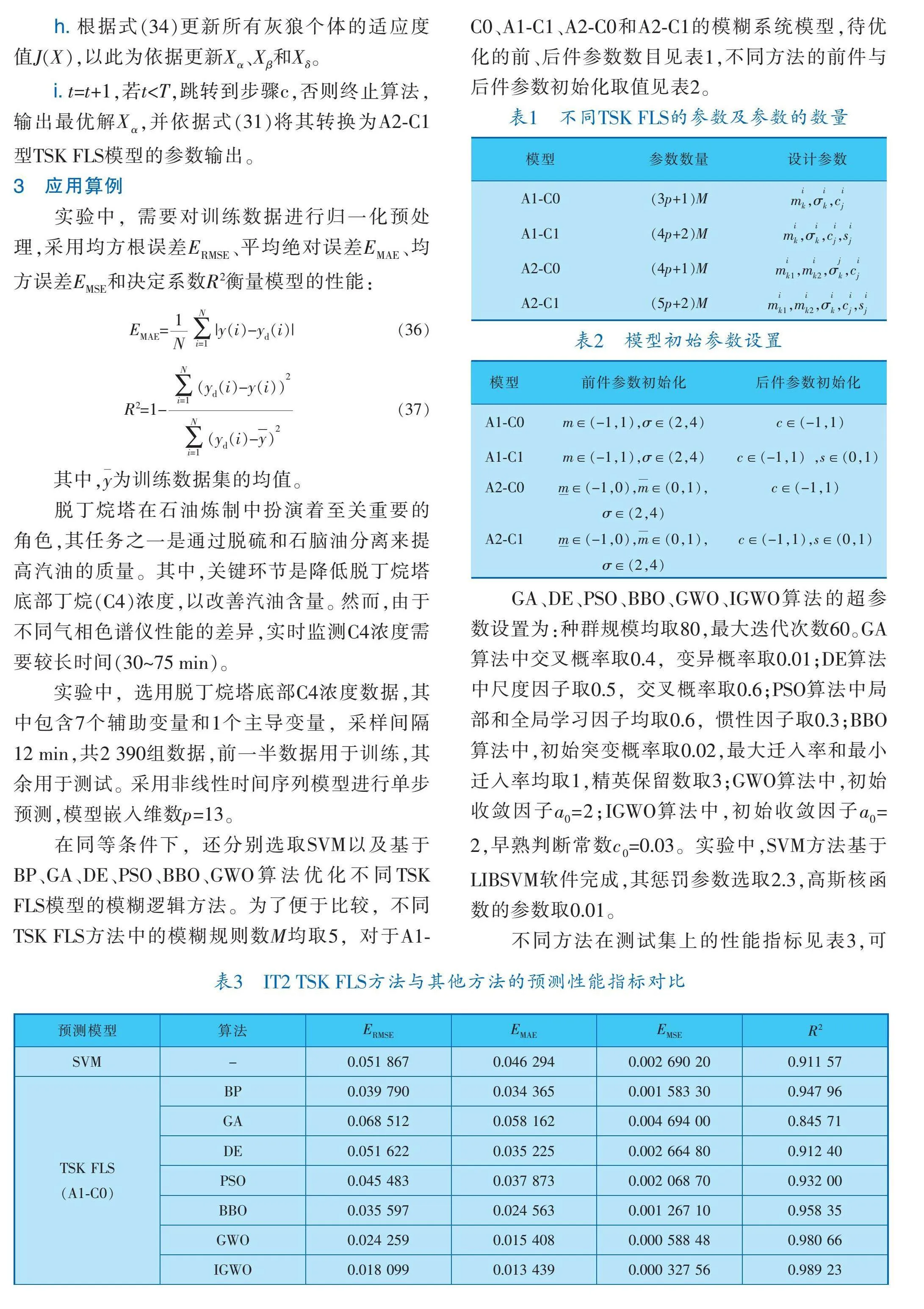
實驗中，需要對訓練數據進行歸一化預處理，采用均方根誤差E、平均絕對誤差E、均方誤差E和決定系數R2衡量模型的性能：

E=｜y（i）-y（i）｜" """"（36）

R2=1-""""" （37）

其中，y為訓練數據集的均值。

脫丁烷塔在石油煉制中扮演著至關重要的角色，其任務之一是通過脫硫和石腦油分離來提高汽油的質量。其中，關鍵環節是降低脫丁烷塔底部丁烷（C4）濃度，以改善汽油含量。然而，由于不同氣相色譜儀性能的差異，實時監測C4濃度需要較長時間（30～75 min）。

實驗中，選用脫丁烷塔底部C4濃度數據，其中包含7個輔助變量和1個主導變量，采樣間隔12 min，共2 390組數據，前一半數據用于訓練，其余用于測試。采用非線性時間序列模型進行單步預測，模型嵌入維數p=13。

在同等條件下，還分別選取SVM以及基于BP、GA、DE、PSO、BBO、GWO算法優化不同TSK FLS模型的模糊邏輯方法。為了便于比較，不同TSK FLS方法中的模糊規則數M均取5，對于A1 C0、A1 C1、A2 C0和A2 C1的模糊系統模型，待優化的前、后件參數數目見表1，不同方法的前件與后件參數初始化取值見表2。

GA、DE、PSO、BBO、GWO、IGWO算法的超參數設置為：種群規模均取80，最大迭代次數60。GA算法中交叉概率取0.4，變異概率取0.01；DE算法中尺度因子取0.5，交叉概率取0.6；PSO算法中局部和全局學習因子均取0.6，慣性因子取0.3；BBO算法中，初始突變概率取0.02，最大遷入率和最小遷入率均取1，精英保留數取3；GWO算法中，初始收斂因子a=2；IGWO算法中，初始收斂因子a=2，早熟判斷常數c=0.03。實驗中，SVM方法基于LIBSVM軟件完成，其懲罰參數選取2.3，高斯核函數的參數取0.01。

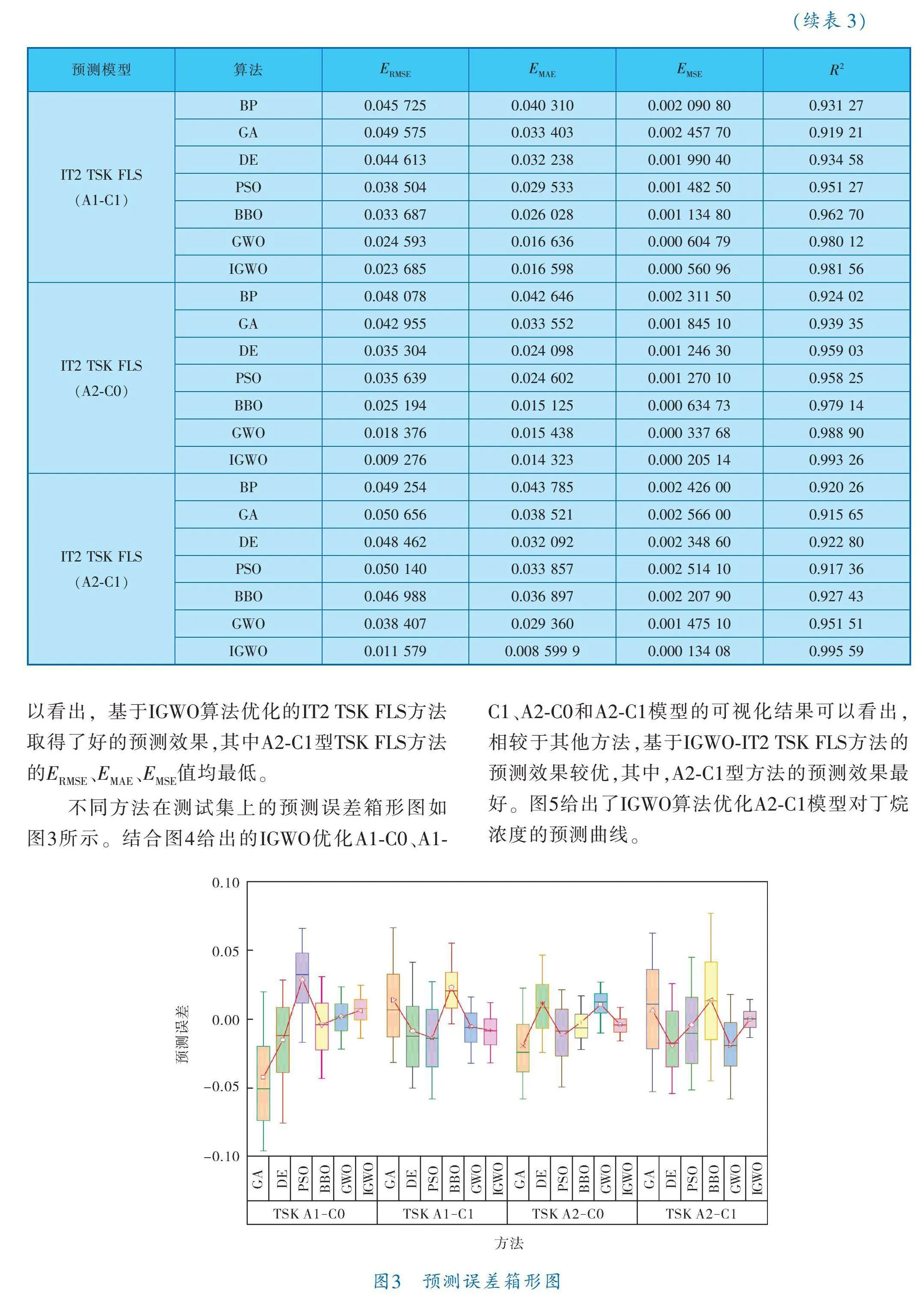
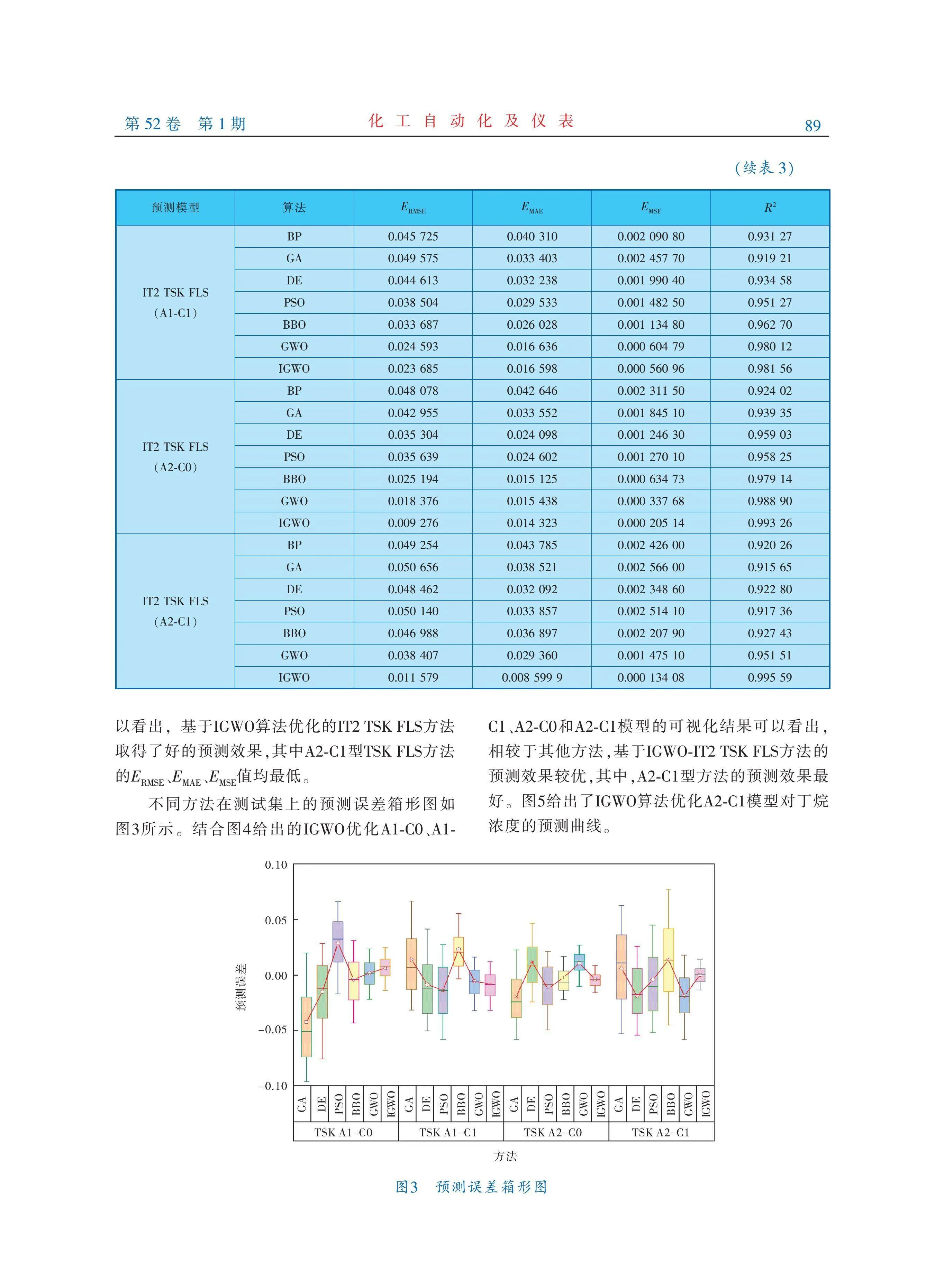
不同方法在測試集上的性能指標見表3，可以看出，基于IGWO算法優化的IT2 TSK FLS方法取得了好的預測效果，其中A2 C1型TSK FLS方法的E、E、E值均最低。

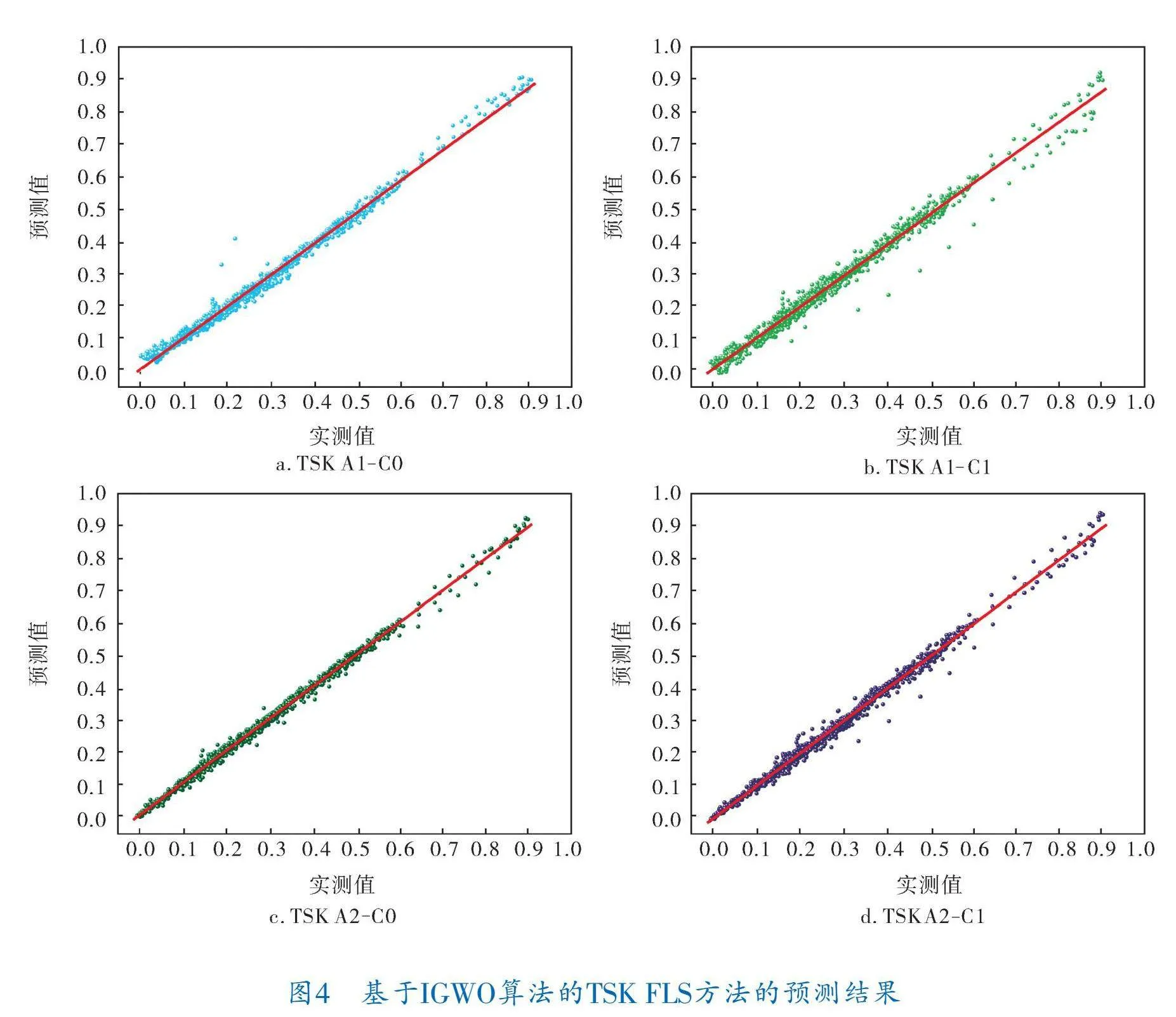
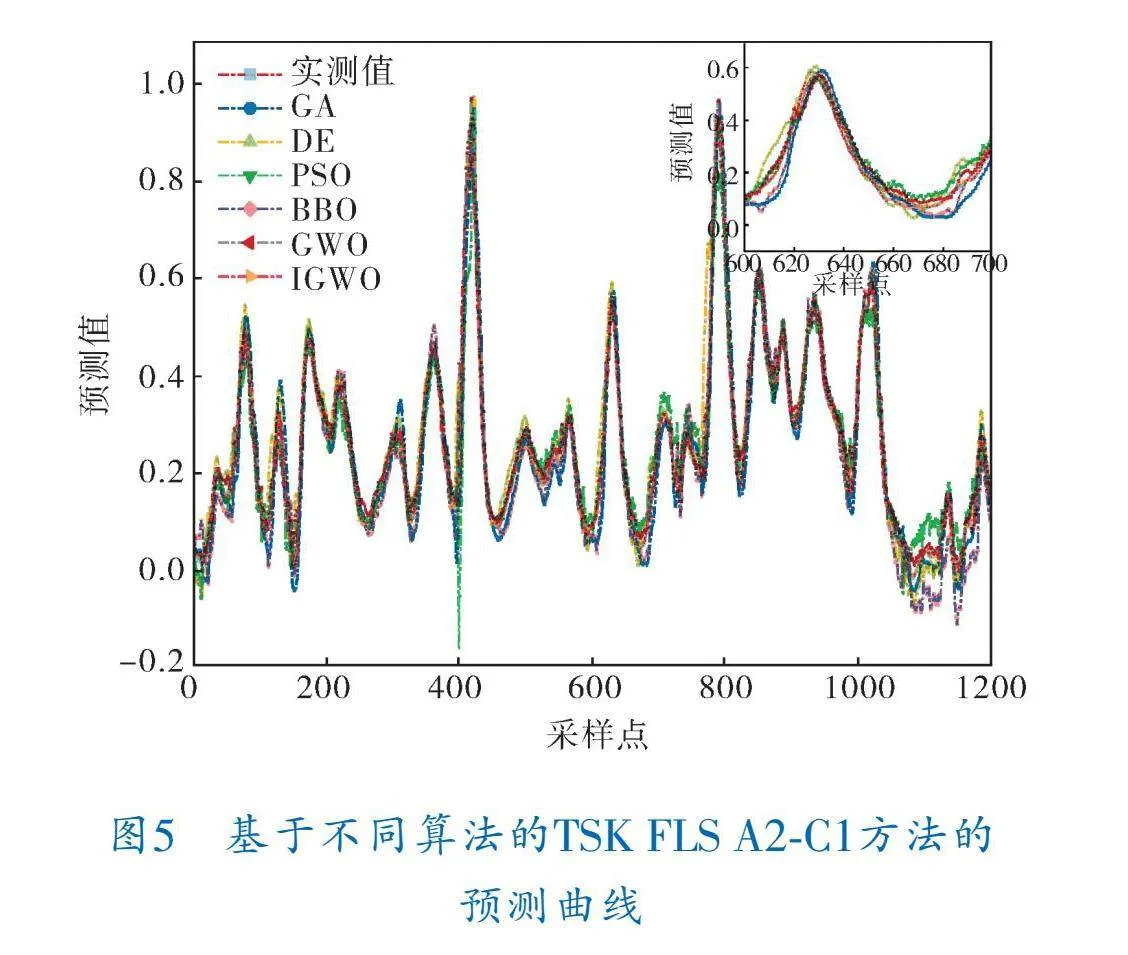
不同方法在測試集上的預測誤差箱形圖如圖3所示。結合圖4給出的IGWO優化A1 C0、A1 C1、A2 C0和A2 C1模型的可視化結果可以看出，相較于其他方法，基于IGWO IT2 TSK FLS方法的預測效果較優，其中，A2 C1型方法的預測效果最好。圖5給出了IGWO算法優化A2 C1模型對丁烷濃度的預測曲線。

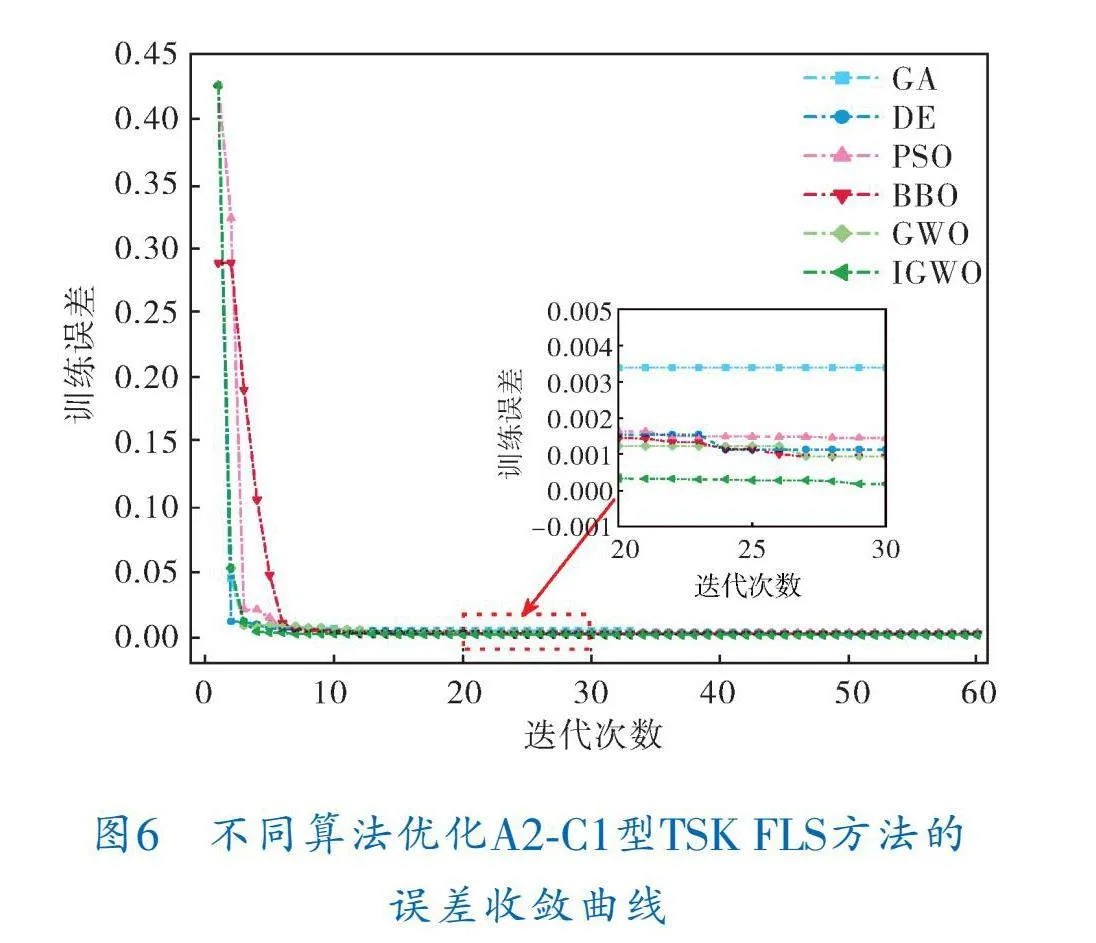
為了衡量IGWO算法性能，以A2 C1型IT2 TSK FLS模型為例，圖6給出了訓練過程中不同優化算法優化模型時訓練誤差隨迭代次數的變化曲線，顯然基于IGWO算法優化的模型在經過約10次迭代后便趨于平穩，其誤差收斂速度較快。

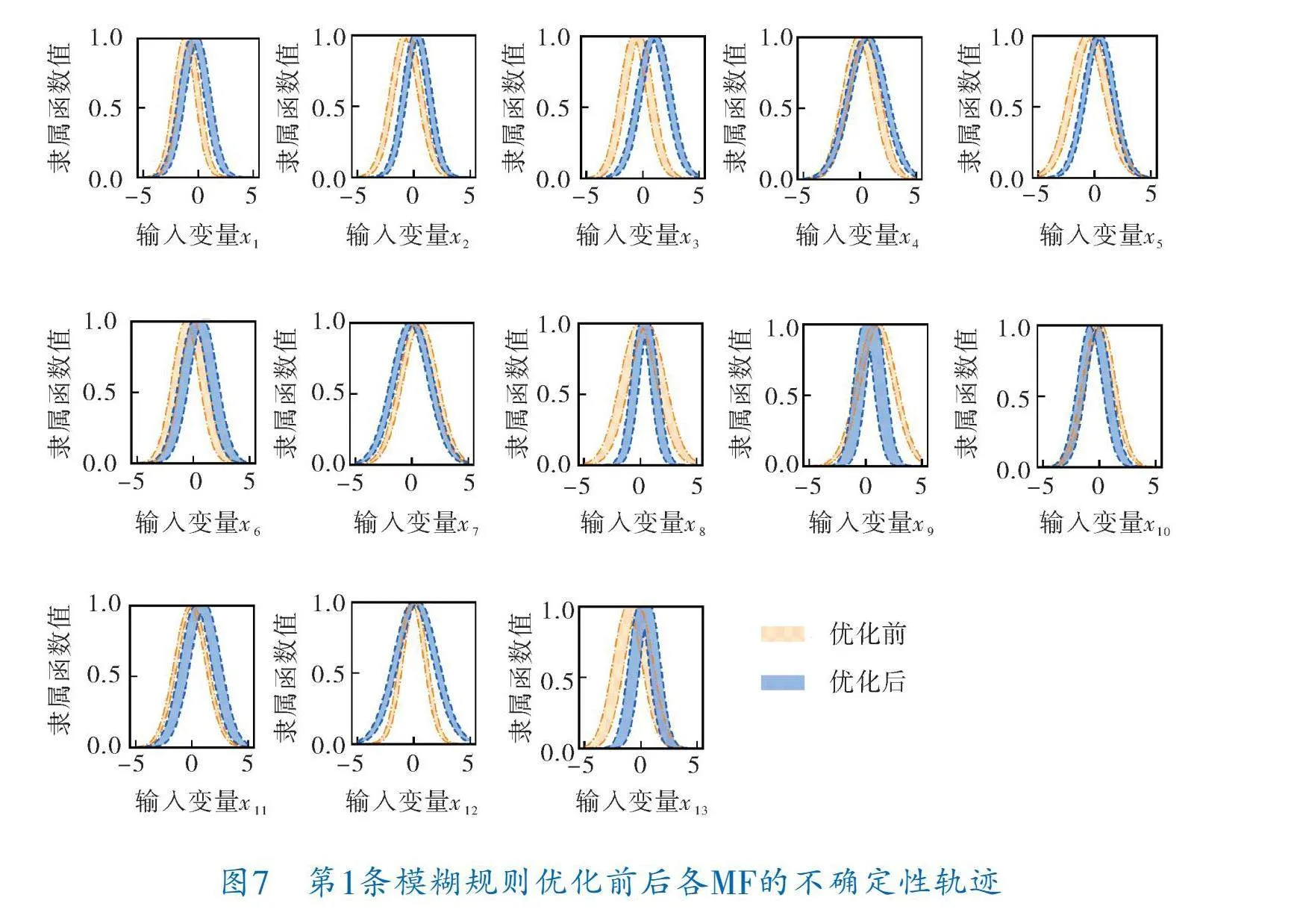
為了更直觀地觀察IGWO算法對模糊前件隸屬函數（MF）的參數優化過程，圖7依次給出了針對A2 C1模型其第1條規則各輸入變量在優化前后MF的變化。相應地，該模型5條規則的后件參數的優化結果見表4。

4 結束語

針對化工軟測量，提出基于IGWO優化TSK FLS方法的前件與后件參數，應用非線性時間序列建模方式，提出IGWO算法優化IT2 TSK FLS的方法。將其應用于脫丁烷塔底部丁烷濃度預測實例中，對所提方法的預測效果進行了檢驗，IGWO算法通過引入早熟收斂判斷機制、收斂因子非線性調整策略、Levy飛行策略，克服了傳統GWO算法易早熟、收斂精度低等問題；IGWO算法具有控制參數少、收斂速度快、不易陷入局部最優等優點，與IT2 TSK FLS方法相結合，在化工軟測量中表現出色，為模型提供了更強的預測建模能力；采用優化算法訓練IT2 TSK FLS，克服了傳統BP算法的局部最優問題，相較于其他方法，預測精度顯著提高。為進一步優化預測效果，可以考慮研究不同優化算法的組合，并將其應用于化工軟測量領域。

參 考 文 獻

［1］ CHEN Z，DING S，PENG T，et al. Fault Detection for Non Gaussian Processes Using Generalized Canonical Correlation Analysis and Randomized Algorithms［J］.IEEE Transactions on Industrial Electronics，2018，65（2）：1559-1567.

［2］ 王強.基于非線性特征提取的軟測量智能建模方法研究［D］.青島：中國石油大學（華東），2015.

［3］ KADLEC P，GABRYS B，STRANDT S. Data driven Soft Sensors in the process industry［J］.Computers amp; Chemical Engineering，2009，33（4）：795-814.

［4］ HE Y L，XU Y，ZHU Q X. Soft sensing model development using PLSR based dynamic extreme learning machine with an enhanced hidden layer［J］.Chemometrics and Intelligent Laboratory Systems，2016，154：101-111.

［5］ QIN S J. Data driven Fault Detection and Diagnosis for Complex Industrial Processes［J］.IFAC Proceedings Volumes，2009，42（8）：1115-1125.

［6］ SOUZA F A A，ARAJO R，MENDES J. Review of soft sensor methods for regression applications［J］.Chemometrics and Intelligent Laboratory Systems，2016，152：69-79.

［7］ YUAN X，ZHOU J，HUANG B，et al. Hierarchical Qua "lity Relevant Feature Representation for Soft Sensor Modeling：A Novel Deep Learning Strategy［J］.IEEE Transactions on Industrial Informatics，2020，16（6）：3721-3730.

［8］ GHOLAMI A R，SHAHBAZIAN M. Soft sensor design based on fuzzy C Means and RFN_SVR for a stripper column［J］.Journal of Natural Gas Science and Engineering，2015，25：23-29.

［9］ LI Q，XING L，LIU W，et al. Adaptive Soft Sensor Based on a Moving Window Just in time Learning LS SVM for Distillation Processes［J］.IFAC PapersOnLine，2015，48 （28） ：51-56.

［10］ NASR M S，MOUSTAFA M A E，SEIF H A E，et al. Application of Artificial Neural Network（ANN）for the prediction of EL AGAMY wastewater treatment plant performance EGYPT［J］.Alexandria Engineering Journal，2012，51（1）：37-43.

［11］ HUANG M，MA Y，WAN J，et al. A sensor software based on a genetic algorithm based neural fuzzy system for modeling and simulating a wastewater treatment process［J］.Applied Soft Computing，2015，27：1-10.

［12］ MENDES J，SOUZA F，ARAJO R，et al. Genetic fuzzy system for data driven soft sensors design［J］.Applied Soft Computing，2012，12（10）：3237-3245.

［13］ LIANG Q L，MENDEL J M. An introduction to type 2 TSK fuzzy logic systems［C］//FUZZ IEEE′99.1999 IEEE International Fuzzy Systems.1999：1534-1539.

［14］ 伍冬睿，曾志剛，莫紅，等.區間二型模糊集和模糊系統：綜述與展望［J］.自動化學報，2020，46（8）：1539-1556.

［15］ MITTAL K，JAIN A，VAISLA K S，et al. A comprehensive review on type 2 fuzzy logic applications：Past，present and future［J］.Engineering Applications of Artificial Intelligence，2020，95：103916.

［16］ DE LOS ANGELES HERNANDEZ M，MELIN P，M NDEZ G M，et al. A hybrid learning method composed by the orthogonal least squares and the back propagation learning algorithms for interval A2 C1 type 1 non singleton type 2 TSK fuzzy logic systems［J］.Soft Computing，2015，19（3）：661-678.

［17］ ZHANG R，TAO J.A Nonlinear Fuzzy Neural Network Modeling Approach Using an Improved Genetic Algorithm［J］.IEEE Transactions on Industrial Electronics，2018，65（7）：5882-5892.

［18］ MONTAZERI GH M，YAZDANI S. Application of interval type 2 fuzzy logic systems to gas turbine fault diagnosis［J］.Applied Soft Computing，2020，96：1067 03.

［19］ MIRJALILI S，MIRJALILI S M，LEWIS A. Grey Wolf Optimizer［J］.Advances in Engineering Software，2014，69：46-61.

［20］ MIRJALILI S. How effective is the Grey Wolf optimizer in training multi layer perceptrons［J］.Applied Intelligence，2015，43（1）：150-161.

［21］ TRIPATHI S，SHRIVASTAVA A，JANA K C. Self Tuning fuzzy controller for sun tracker system using Gray Wolf Optimization（GWO）technique［J］.ISA Transactions，2020，101：50-59.

［22］ HEIDARI A A，PAHLAVANI P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks［J］.Applied Soft Computing，2017，60：115-134.

［23］ 何思名，袁智勇，雷金勇，等.基于改進灰狼算法的DG接入配電網反時限過電流保護定值優化［J］.電力系統保護與控制，2021，49（18）：173-181.

［24］ TRAN C N，PARK D C.MPEG Video Traffic Modeling and Classification Using Fuzzy C Means Algorithm with Divergence Based Kernel［C］//Neural Information Processing.2006：439-447.

［25］ 董飛飛，劉滌塵，吳軍，等.基于改進BBO優化算法和電網生存性的核心骨干網架構建［J］.中國電機工程學報，2014（16）：2659-2667.

［26］ 印雷，顧德，劉飛，等.基于改進麻雀搜索算法優化的DVHop定位算法［J］.傳感技術學報，2021，34（5）：670-675.

［27］ AMIRSADRI S，MOUSAVIRAD S J，EBRAHIMPOU R KOMLEH H.A Levy flight based grey wolf optimizer combined with back propagation algorithm for neural network training［J］.Neural Computing and Applications，2018，30（12）：3707-3720.

（收稿日期：2023-12-04，修回日期：2024-10-18）

Application of IGWO Optimization Algorithm based Interval Type 2 TSK FLS Method in the Soft Measurement of Chemical Process

ZENG Yu xiang1， ZHANG Shuan2

（1. Tianhua Chemical Machinery and Automation Institute Co.，Ltd.；

2. Henan JK Chemical Investment Holding （Group）Co.， Ltd.）

Abstract"" Considering strong nonlinearity and complexity in the soft sensing modeling for chemical process， a IGWO IT2 TSK FLS method was proposed based on interval Type 2 Takagi Sugeno Kang fuzzy logic system and combined with an improved grey wolf optimizer. Compared with the TSK fuzzy logic system， the IT2 TSK FLS method adeptly captured both intra individual and inter individual uncertainties. On the basis of the existing error back propagation （BP） algorithm training， the IGWO algorithm was further used to design model’s input and output so as to improve prediction performance of the model. Through improving the grey wolf optimization algorithm， the premature convergence judgment mechanism， nonlinear cosine adjustment strategy and Levy flight strategy were introduced to improve convergence speed of the algorithm and avoid its falling into local optimum. In addition， the IGWO IT2 TSK FLS method was applied to the modeling of the soft sensing examples for a debutane tower. Under the same conditions， having the IGWO IT2 TSK FLS method compared with the type 1 TSK FLS method， BP algorithm， GA， differential evolution （DE）， PSO， biogeography based optimization （BBO） and grey wolf optimization （GWO） was implemented， respectively. The experimental results show that， the IGWO IT2 TSK FLS method outperforms them in performance， including its effectiveness and application potential.

Key words"" IGWO IT2 TSK FLS method， debutane tower， soft sensor modeling， premature convergence judgment mechanism， nonlinear cosine adjustment strategy， Levy flight strategy