Ｅｘｃｅｌ雙解物理極值問題

湯朝紅　肖發新

Excel不僅是制表軟件，而且是一種功能強大的數據統計和分析工具，能進行復雜的公式運算。對于物理中的極值問題，我們既可以通過Excel所繪制的函數圖像直接讀出，也可以利用“規劃求解”功能快速、準確地加以解決。我們以一個常見的拋體問題為例，說明如何使用Excel通過兩種不同的方法解決物理極值問題。

我們知道，在忽略空氣阻力的情況下，從水平面斜向上拋出的物體，其水平射程在拋射角 ＝45°時最遠。更為常見的情形是從距地面一定高度的地方斜向上拋出，此時最佳拋射角與拋射速度和拋射高度這兩個初始條件的大小有關。在這種情況下，拋射角取多少時水平射程最大呢？我們列出水平和豎直兩個方向上的運動方程：

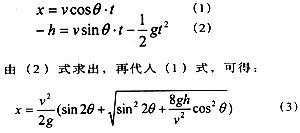
如果我們將水平射程理解為兩部分水平位移之和，即由和組成（圖1）。第一部分表示=0時的水平射程。第二部分表示從高度為的地方斜向下拋向地面所產生的水平位移。當拋射角＝45°時，取得最大值，但此時進行斜下拋時具有較大的豎直速度，無法取得最大值；如果為了增大而取一個小于45°的，又無法取得最大值，因此應介于0°和45°之間。對于給定的和，我們可以利用（3）式求出最佳的拋射角和的最大值。

以=15.0m/s，=25.0m為例，我們將利用Excel的繪圖功能和“規劃求解”功能，使用兩種不同的方法求解上述條件下的最佳拋射角和水平射程 的最大值。

一、圖像求解法

1．在A1單元格中輸入“ ”， A₂、A₃單元格分別輸入“0”、“1”，用鼠標選中A₂和A₃單元格，將鼠標移到A3的右下角，當鼠標的符號變為“+”時，按住鼠標向下拖，Excel會自動地以公差為1的等差數列來填充，直到A47，此時A47單元格中的數值為45。

2．在B1單元格中輸入“ ”，在B2單元格中依據上文（3）式輸入公式“=15*15/(2*9.8)*(sin(2*A₂/180*3.14)+SQRT(sin(2*A₂/180*3.14)^2+8*9.8*25/(15*15)*cos(A₂/180*3.14)^2))”，回車確定。選中B₂單元格，將鼠標移到B₂的右下角，當鼠標的符號變為“+”時，按住鼠標一直向下拖到B47單元格內，Excel自動計算出了每一個對應的值。

3．選取A、B兩列數據，依次點擊菜單[插入]—[圖表]，即出現[圖表向導]窗口，在[圖表類型]中選擇[X、Y散點圖]，在[子圖表類型]中選擇[無數據點平滑線散點圖]，點擊[下一步]，在相應位置輸入圖表名稱、坐標軸名稱，點擊[完成]。接下來，我們可以對圖表的繪圖區、坐標軸和網格線等部分進行相應的修改，直至如圖2所示。

觀察圖2，我們可以發現在28ο～30ο之間有最大值，可以用Excel的查找功能在數據區域找到精確值。或者在圖像中直接用鼠標指向曲線的最頂端，此時在鼠標的右下方會顯示相應的精確值。結果表明當=29°時，有最大值40.927m。

二、“規劃求解”法

用上面的圖像法求得的=29°和X_max其實是一個近似解，利用Excel提供的“規劃求解”功能則可以求出拋射角的精確解。Excel的“規劃求解”允許我們根據目標函數及其約束條件自動調整多個變動因素，以期找到問題的最優解，從而方便地解決許多物理極值問題。下面仍以=15.0m/s，=25.0m為例，方法如下：

在A₁單元格中輸入變量“ ”，在B1單元格中輸入上文（3）式的表達式：“=15*15/(2*9.8)*(sin(2*A1/180*3.14)+SQRT(sin(2*₁/180*3.14)^2+8*9.8*25/(15*15)*cos(₁/180*3.14)^2))”，回車確定。

“規劃求解”功能在默認情況下是沒有安裝的，我們首先必須進行安裝。選擇[工具]菜單中[加載宏]選項，在安裝提示下裝入[規劃求解]（注意要插入安裝盤）。也可以將安裝盤中[Pfiles]—[Office]—[Library]下的[Solver]文件夾及其目錄下的Solver.xla、Solvr32.dll復制到Office安裝目錄[Office]—[Library]下，然后加載即可。

在[工具]菜單中選擇[規劃求解]，在彈出的[規劃求解參數]對話框中通過點擊B1單元格，使[目標單元格]出現$B$1的絕對引址。鑒于我們要求解的是最大值，于是在[等于]中選擇[最大值]。在[可變單元格]中通過點擊A1單元格，使之在框內出現$A$1的絕對引址。在[約束]處按[添加]，在隨后出現的[添加約束]對話框中的[單元格引用位置]處點擊A1單元格使之出現$A$1，在后面的框內選“<=”，“約束值”填入45，最后得到“$A$1<=45”。與之類似，添加約束條件“$A$1>=0”（圖3）。

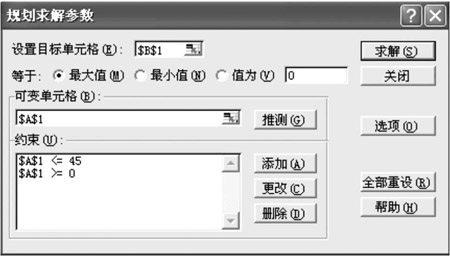
最后，點擊[求解]按鈕，選[保存規劃求解結果]，按[確定]。我們在A1和B1單元格得到了29.306和40.928兩個精確解，即當=29.306°時， 有最大值40.928m。