“函數(shù)的單調(diào)性”教學設計

教學目標

認識目標：掌握函數(shù)單調(diào)性的概念；會判斷一些簡單函數(shù)的單調(diào)性。

能力目標：培養(yǎng)學生的分析、歸納和總結能力；培養(yǎng)學生運動變化和數(shù)形結合的數(shù)學思想；培養(yǎng)學生理論聯(lián)系實際的辯證唯物主義思想。

情感目標：營造親切、活躍的課堂氣氛，實施多元化評價，激勵學生，使學生嘗試成功，以點燃學生的學習熱情。

教學重點、難點

重點：函數(shù)單調(diào)性概念和函數(shù)單調(diào)性的判斷。

難點：判斷函數(shù)的單調(diào)性。

教學過程設計與分析

創(chuàng)設問題情境

多媒體：學校的簡介。（利用Flash進行演示）

提出問題：學校準備建造一個長方形的花壇，面積設計為16平方米。由于周圍環(huán)境的限制，其中一邊的長度長不能超過10米，短不能少于4米，求花壇半周長的最小值和最大值。

教師說明：此環(huán)節(jié)為創(chuàng)設情境。我們學校是上海市投資新建的郊區(qū)四所寄宿制重點高中之一，有著一流的硬件設施，綠化建設正在進行之中。抓住這一點，我設計了這節(jié)課的引例，切合實際，讓學生有種親切感。提出問題后，讓學生思考、討論下列問題：如何把實際問題歸結為數(shù)學問題？經(jīng)過思考、討論，估計學生可以把問題歸結為：設受限制一邊長為x米，4≤x≤10，則另一邊為16/x米，求半周長y＝x＋16/x（4≤x≤10）的最小值和最大值。如何求最小值？——運用基本不等式。如何求最大值？經(jīng)過思考、討論，最后大家一致認為利用y＝x＋16/x（4≤x≤10）的圖像可以得出結論。

多媒體：利用Flash演示y＝x＋16/x（4≤x≤10）的圖像,如圖1所示。

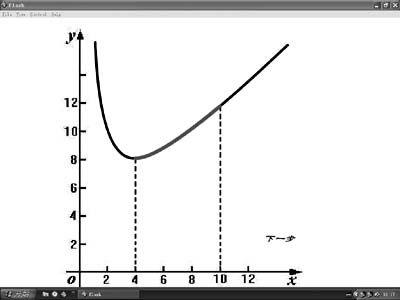
教師說明：利用Flash給出函數(shù)的圖像，從函數(shù)圖像可以直觀地得出結論，但是缺乏理論依據(jù)。指出缺乏理論依據(jù)的結論是站不住腳的，所以問題轉化為尋找其理論依據(jù)，從而引入課題。這樣可以培養(yǎng)學生嚴謹?shù)闹螌W態(tài)度。

揭示課題，引入新課

1.幾何畫板演示，點明課題。

多媒體：利用幾何畫板演示y＝x＋16/x（4≤x≤10）的動態(tài)的變化過程。用鼠標從左向右緩慢拖動y＝x＋16/x（4≤x≤10）上的A點，引導學生觀察A點的縱坐標的變化情況（隨著自變量x的增大，函數(shù)值y也在增大），如圖2所示。

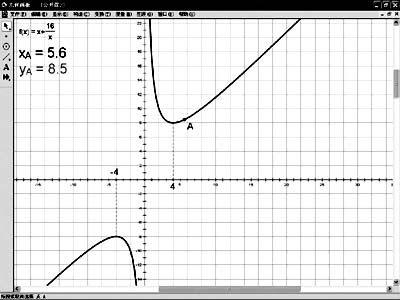
2.請學生根據(jù)自己的理解給出增函數(shù)定義。

一般地，對于給定區(qū)間上的函數(shù)f(x)：如果對于屬于這個區(qū)間的自變量的任意兩個值x₁和x₂，當x₁＜x₂時，都有f(x₁)＜f(x₂)，那么就說函數(shù)f(x)在這個區(qū)間上是增函數(shù)。

3.請學生通過類比得出減函數(shù)的定義。

教師說明：在減函數(shù)定義的教學過程中，我改變了以往“灌輸結論”的做法，讓學生通過對增函數(shù)定義的理解從而得到減函數(shù)的定義，培養(yǎng)了學生的類比的重要數(shù)學思想方法，對于學生學習新知識、新概念有很大的幫助。

鞏固新知，深化擴展

1.一次函數(shù)的單調(diào)性問題。

[例1]證明函數(shù)f(x)＝3x＋2在區(qū)間(－∞，＋∞)上是增函數(shù)。

引申：探索一次函數(shù)f(x)＝kx＋b(k≠0)在區(qū)間(－∞，＋∞)上的單調(diào)性。

2.二次函數(shù)的單調(diào)性問題。

[例2]判斷函數(shù)f(x)＝x₂－2x的單調(diào)區(qū)間，并加以證明。

教師說明：例題的給出由簡單的一次函數(shù)到二次函數(shù)，遵循了學生一般的認知規(guī)律，使學生容易接受，易于理解。在二次函數(shù)f(x)＝x²－2x的單調(diào)性的證明中，分工合作，第一、二組的學生完成函數(shù)在[1，＋∞)上的證明；第三、四組的學生完成函數(shù)在(－∞，1]上的證明，倡導自主學習、合作學習的新的學習方式。通過例1、例2的解決，讓學生歸納判斷函數(shù)單調(diào)性的基本步驟，培養(yǎng)學生分析、歸納和總結的能力。

判斷函數(shù)單調(diào)性的基本步驟：

第一步，設x₁、x₂是區(qū)間內(nèi)的任意兩個實數(shù)，且x₁＜x₂。

第二步，比較f(x₁)、f(x₂)的大小。

第三步，給出結論。

自主解決——[引例]的解決

教師說明：有了上述理論作基礎，一開始提出的問題就能迎刃而解：證明函數(shù)y＝x＋16/x在區(qū)間[4，10]上是增函數(shù)；得出結論，當x=10時，y_max=11.6。此環(huán)節(jié)起到了首尾呼應的作用，讓學生體會到數(shù)學源于生活又服務于生活，體會到數(shù)學的魅力，并指出，函數(shù)單調(diào)性的研究為解決函數(shù)的最值問題提供了又一重要方法，可見研究函數(shù)的單調(diào)性是非常有必要的。那么我們?yōu)楹尾怀藙僮窊簦剿鞲话愕那闆r，研究函數(shù)y=x+k/x(k∈Ｒ)的單調(diào)性。

多媒體：利用Authorware進行探索、總結y=x+k/x(k∈Ｒ)圖像，尋找一般的結果。（從特殊到一般）如圖3、4所示。

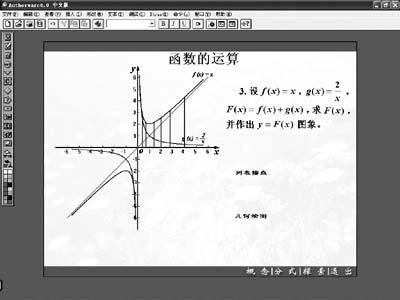
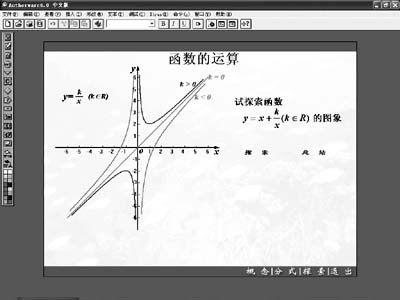
學生總結、教師歸納

教師說明：提出問題，這節(jié)課你學到了哪些數(shù)學知識？學生一一羅列：函數(shù)單調(diào)性的概念、判斷函數(shù)單調(diào)性的常用方法、證明函數(shù)單調(diào)性的基本步驟。進一步提出問題：整堂課體現(xiàn)了哪些重要的數(shù)學思維？自問自答：從特殊到一般的研究方法；從大膽的猜想到嚴格的證明；數(shù)形結合、類比的思想。利用計算機使我們探索數(shù)學問題的過程更加直觀、簡潔和生動。

（作者單位：上海市南匯中學 201300）

點評

“問題是數(shù)學的心臟”。一個好的問題能引起學生興趣，啟迪學生的思考，將思維引向深刻。閔麗紅老師的“學校花壇問題”是一個很好的實際問題：在學校綠化建設中，如何建造其費用最省？閔老師通過引導學生觀察問題、發(fā)現(xiàn)問題、提出問題、探究和解決問題，使學生感受到數(shù)學源于生活又服務于生活，以培養(yǎng)學生形成科學觀，培養(yǎng)學生的創(chuàng)新精神和實踐能力。

這節(jié)課最大的特點是貫穿始終的現(xiàn)代軟件技術的應用，嫻熟地運用了PowerPoint、Authorware、Flash和幾何畫板等多種教學媒體和手段，通過直觀的畫面和動態(tài)的影像，將數(shù)學知識的發(fā)生和發(fā)展淋漓盡致地展現(xiàn)在學生面前。尤其在利用Authorware進行探索、總結圖像的過程中，首先，研究特殊情況（當k=2時）,使用列表描點、幾何繪圖兩種方法，利用計算機動態(tài)地繪畫出它的圖像。緊接著，探索、總結其一般結果：隨機地輸入k的值，隨即電腦顯示相應函數(shù)的圖像。最后，顯示所有情況，一目了然，使每位學生對于圖像都有了清晰的、精確的認識。利用多媒體處理這一部分達到的效果，是傳統(tǒng)教學所不及的，充分地體現(xiàn)了現(xiàn)代技術的優(yōu)越性。

現(xiàn)代建構主義的教學觀認為，知識并不能簡單地由老師傳授給學生，而主要由每個學生依據(jù)自身已有知識和經(jīng)驗主動地加以建構。閔老師理解了這一觀點的精髓，改變了以往單一被動的學習模式，提倡主動探索、合作學習，體現(xiàn)了上海市二期課改的精神，是一節(jié)成功的公開展示課。