殺菌劑生物測定動態評價時間-劑量-抑菌率模型
唐 潔 唐啟義 孫傳恒 沈愛華
摘要根據互補重對數數學模型的原理,建立了動態評價殺菌劑抑菌效應的時間-劑量-抑菌率模型,給出了模型參數估計和統計檢驗方法.并重點討論了劑量的時間效應和不同時間段的劑量效應。最后提供了該模型的計算機算法實現和應用例子。
關鍵詞農藥學;殺菌劑生物測定;時間-劑量-抑菌率模型;動態訐價
中圖分類號S481.9
用于防治植物病害的殺菌劑均以某種方式影響病原菌的生長過程。因此測定其抗菌活性對殺菌劑的研究具有重要意義。在評價殺菌劑作用大小時,將藥劑以某種形式添加到培養基中,觀察制劑對病菌生長的影響。常用試驗方法是用瓊脂平板培養法來評價殺菌劑抑菌作用。這類試驗,當菌塊接種到含一定濃度藥劑的瓊脂培養基平板上,然后在一定條件下培養,經過一段時間(為對照培養皿菌落即將長滿時),測定各個處理菌落擴展直徑(面積),并與不添加藥劑的處理(對照)相比較,以相對抑制率作為抑菌效果好壞的指標,評價各個處理最終的抑菌效果。但是,傳統的方法沒有將時間作為一個因素進行考慮,不能反映殺菌劑生物測定的時間動態,導致時間與劑量的效應相互分開,無法使試驗效果的評價指標充分體現實驗數據的完整性。因此,有必要將時間和劑量效應統一到同一個抑菌效果評價模型中來。本研究根據近年用于殺蟲劑生物測定分析的重對數互補數學模型(complementary logdogmodel)的原理,建立動態評價殺菌劑抑菌效應的時間-劑量-抑菌率模型(Time-dose-inhibitingmod-el,TDl)。





分析前在DPS數據處理系統中,先將數據整理如表1形式,應用DPS軟件提供的時間-劑量-抑菌率模型分析功能分析,可得到如下解釋的所有結果。
DPS首先給出了各個處理時間內還可利用空間的累積減少率pij及按式(2)汁算各個處理時間內可利用空間的相對減少率ij。并應用非線性最小二乘法優化式(3),即使條件概率的觀察值和理論值的均方擬合誤差達到最小。
4殺菌劑生物測定時間-劑量-抑菌率模型的計算機算法實現
如前所述,估計時間-劑量-抑菌率模型的參數Y需應用非線性最小二乘法進行估計。這里采用Pascal語言,應用Marquart非線性最小二乘法進行迭代汁算,估計出有關參數并進行統計檢驗,只要按表1格式輸入數據,即可進行分析,并得到所有參數估計值、統計檢驗結果及各個時段抑菌效應的LD50估計和各個處理劑量時的抑菌效應的LT50估計。
5應用舉例
如應用某種化學制劑,在面積為5805 mm2的培養皿中處理某真菌病原菌。處理及試驗結果如表1。從表1可以看出,處理后菌叢擴展過程緩慢.如按傳統分析方法,不能反映抑菌率的動態變化過程,故適合采用TDI模型進行分析。
通過計算機處理,本例試驗數據的計算結果為其時間-劑量-抑菌率模型的總體檢驗,即對模型進行方差分析,其F統計量等于148.4155,顯著水平p<0.0001,確定系數r2=0.9808,因此可認為模型總的擬合效果良好。從各個參數的統計檢驗可以看出,β=-3.1903,顯著水平p<0.0001其他參數,即各個時段系數r1的估計值和t槍驗結果如表2,各個系數均達到極顯著水平。根據式(4)給出相應時段的抑菌效應參數,的估計值(表2)。
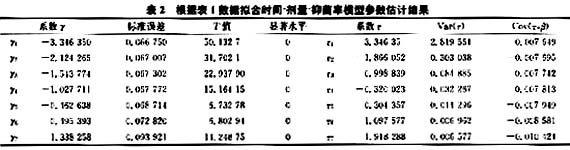
在模型參數估計結果基礎上,根據式(5)可得到處理后不同時期的致死中濃度的對數值,即lg(LD50),以及lg(LD90)和其標準誤的估計(表3)。根據式(6)得到各個劑量的時間效應指標.即致死中時間LT50,以及LT90的估計(表4)。

6討論
殺(抑)菌劑的生物測定,目前一般用抑菌率作為評價指標,這是將殺(抑)菌率作為藥劑對目標對象的一個靜態度量處理,但實際上,由于殺(抑)菌劑對牛物體的作用有一個過程.而這個過程應該是動態的,所有原有的評價指標不能反映這種動態的作用效應。在殺蟲劑的生物測定中,Preister等將重對數互補模型應用于劑量一時間效應的分析。唐啟義等將該模型收錄到出版的統計軟件中,馮明光等已應用該模型于殺蟲劑的生物測定方面,并取得了良好效果,顯示出該模型是迄今為止較為理想的生測數據分析方法。本文將該模型根據殺(抑)菌劑的作用特點,根據重對數互補數學模型,提出了建立動態評價殺菌劑抑菌效應的時間-劑量-抑菌率模型的參數估計和統計檢驗方法,使之可用于殺菌劑的生物測定分析。該模型不僅數學模型本身結構科學、嚴謹,各個參數有明確的生物學含義,而業可以動態評價殺菌劑的殺菌、抑菌效應。因此該模型將是植物病理工作者和從事農藥外發的科研工作者的有力工具。

