基于MSC.Patran的水翼升力求解方法研究
, ,, ,
(1.江南大學信息工程學院, 江蘇 無錫 214122; 2.中國船舶科學研究中心, 江蘇 無錫 2140821)
對于水翼船船體,在翼行狀態下,船體完全離開水面,船體重量僅由首尾水翼支撐。傳統的研究方法需要在不同條件下進行試驗,每次試驗都需要調整多種參數,如水翼的安裝角度和水翼支柱的高度等,準備工作較為繁雜,這就需要找到一種參數化建模的方法,減少手工勞動。
根據水翼升力面理論計算方法,結合大量的水翼試驗,中國船舶科學研究中心摸索出一套計算任意平面形狀水翼的升力面計算方法,本文在此基礎上使用MSC.Patran作為開發和使用平臺實現了水翼升力求解方法[1]。
1 原理及求解
高速航行時,水翼在水中前進并獲得升力,把船身托出水面,只有水翼、螺旋槳和舵等在水下,系統原理見圖1。
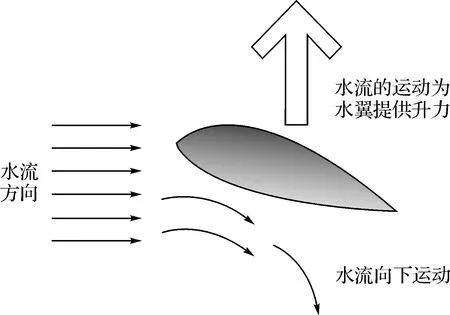
圖1 系統原理
設一水翼在水面下h浸深,在原為靜止的水面下以常數U沿x負方向運動,根據運動轉換原理,相當于水翼處于來流速度為U的來流中。o-xyz為固定在靜止水面上的右手直角坐標系,自由面為xy平面,z軸垂直向上[2]。
考慮水為不可壓縮、無旋、非粘性以及密度均勻的理想流體,則流場中必定存在一擾動速度勢函數φ(x,y,z),在整個流場中滿足Laplace方程,即 :
2φ=0
(1)
總速度勢的求解,還需要滿足邊界條件。
1) 在水翼組合體表面Sb上,擾動速度勢φ應滿足以下物面邊界條件,即速度不穿透物體表面:
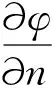
(2)
2) 擾動速度勢φ滿足遠前方無波條件及無限深水中擾動速度為零的條件,即
φ|∞→0
(3)
3) Kutta條件,即在水翼的尾緣處速度為有限值。
|vt,e|<∞
(4)
4) 假定興波是微幅波,滿足線性自由面邊界條件,可分為兩部分
(1) 運動邊界條件:
φ·(y-ζ)=0
(5)
(2) 動力邊界條件:

(6)
式中:ζ——自由面波高。
假設平行流速度勢為U∞=(U∞,0),則由式(5)、(6)顯性化后得到邊界方程:
(7)
根據(6)可以求得自由面波高:
(8)
對于升力繞流問題,尾流可簡化成從物面后緣向后泄放的薄渦層,并進一步抽象為無厚度的空間曲面Sw。在此面上允許速度勢不連續,但要求在該面兩邊的法向導數連續。
利用Green定理,滿足方程 (1),(3),(7)的擾動速度勢φ(x,y,z)可表示為:
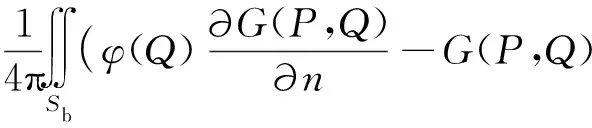
(9)
利用上述邊界條件求得翼形上的偶流強度(速度勢)和水面上的源流強度,由這些奇點強度計算翼形上的速度勢,然后由速度勢沿翼形切線方向的梯度求得切向速度|Vt|,代入Bernoulli方程計算壓力P,而各點壓力系數CP為:
(10)
則升力系數CL和阻力系數CD為:
(11)
(12)
2 實現過程
水翼升力求解主要有三個步驟,見圖2。
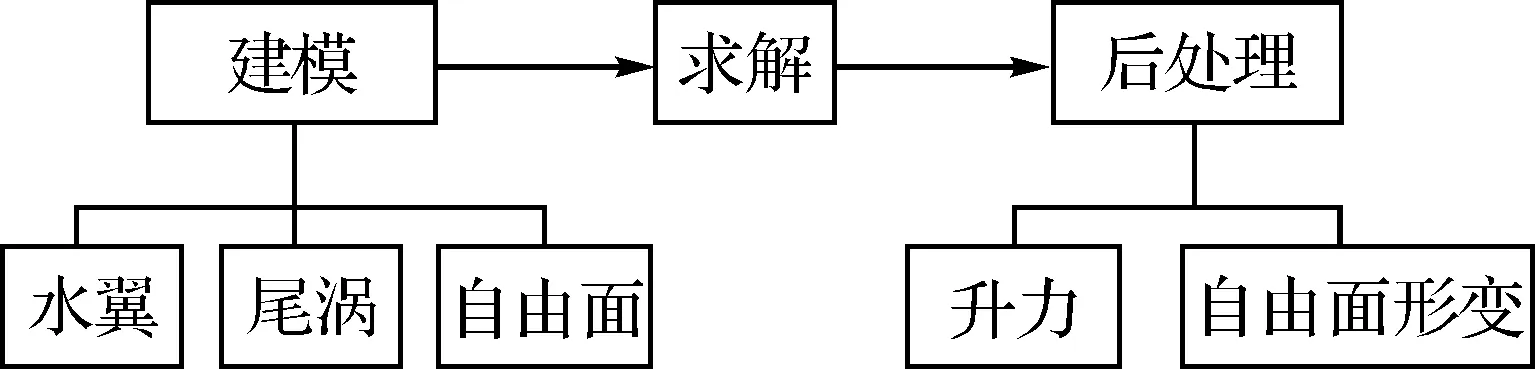
圖2 水翼升力求解系統實現過
2.1 參數化建模
經驗表明,有限元建模在整個有限元分析中占70% ~80%的工作量[3]。而且在目前的有限元建模中,一般為交互式,如果改變某些參數,就需要重新建模,勢必增加工作量。如一個模型有3個參數,每個參數取10個樣本,就要建立1 000個模型。這樣就不能很好地適應產品設計時的動態特性,影響了設計的自動化程度和設計效率 。在以往的實驗中,往往采用兩種方法對不同水翼模型結果進行對比,然后擇優:(1)模型試驗擇優,這樣需要消耗大量的人力和物力,而且所需要的時間長,不能滿足初步設計的要求;(2)理論設計擇優,需要重復進行模型建立和網格劃分,工作量巨大。
因此,考慮使用關鍵參數,結合計算機的高效率,將幾何建模,模型修改和有限元劃分的繁瑣工作提交給計算機來完成,集中精力分析得到的數據和結果,選出最優方案。系統以MSC.Patran作為開發平臺,使用參數化建模,縮短了整個模型設計的周期,并能根據用戶的要求建立不同的模型,方便修改,提高工作效率。
進行參數化建模需要確定模型幾何特征參數和有限元特征參數[4],系統把二者同時作為設計變量,將幾何特征參數的作用范圍延拓至有限元模型,使有限元模型根據參數變化而變化,實現有限元模型的參數化。見圖3所示。

圖3 參數化建模流程
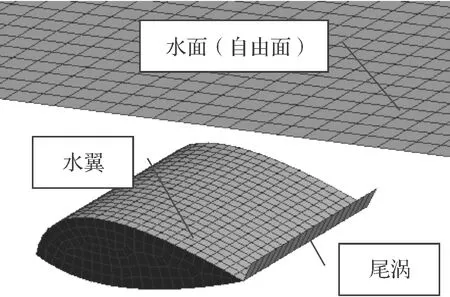
圖4 參數化建模的實
2.2 建立工況并求解
建立工況就是測試水翼在各種條件下的狀態,每一組工況包括工況名、來流速度vx、vy、vz,高速并非對稱。建好的工況將直接保存在db中。
建立工況時,程序使用了PCL的client_data類管理和處理工況數據。client_data類似于數據結構中堆的概念,使用(ID, Client Label, Client Type)方式標識一個數據集合。label在MSC.Patran數據庫中數據集合的唯一標識,type是這種數據集合的識別類型,但是對每一個數據集合的存取借助于地址ID完成。如為工況數據的類型和標簽定義如下:
#define phases_set_client_type 20
#define phases_set_client_label 2000
則工況數據則從label為2000開始借助下面兩個函數存取client_data數據:
get(type, name,n_l, n_i, n_r, n_s, p_l, p_i, p_r, p_s );
set(type, label_start, name, n_l, n_i, n_r, n_s, p_l, p_i, p_r, p_s )。
一個現有的求解器(*.exe)已經被封裝在特定的文件夾內,計算的時候系統把所選擇工況對應的參數傳入求解器中,然后調用求解器進行計算。最后把計算出來的結果保存在一個*.dat和一個*.plt文件中。為了進行后處理,系統將這兩個文件的結果經過數據轉換保存到MSC.Patran的數據庫中。其中從*.dat文件中獲得阻力系數、總面積、升力系數和總投影面積,而從*.plt中獲得自由面所有節點在計算前后發生的位移。
2.3 后處理
求解結束后,將保存在db中的數據在MSC.Patran中進行后處理[5],生成云圖、算出自由面形變以及顯示升力大小。
系統在求解得到的*.plt文件中取出位移后的點坐標,然后根據初始坐標計算出自由面中所有點的位移,得到自由面的形變,并保存到結果工況中,最后在Patran中顯示出來。
3 水翼升力求解數值計算及結果分析
3.1 算例一數值計算及結論
使用參數化建模,創建一塊平板水翼,通過不同浸深和功角,求解出升力系數和自由面波峰,得出定性結論,通過專業人員驗證,結論正確,證明該方法的有效性。以下是建模的主要參數:
水翼 單截面,網格尺寸0.5;
尾渦 尾渦長度1.0;
自由面 起始位置[0 0 0],長度(x方向)10,寬度(y方向)4,網格尺寸0.5;
工況參數 來流速度vx:5.0,vy:0,vz:0.0, 非對稱:False。極高速:False。
表1表明,當水翼浸深h增大時,對自由面形變影響減小;當攻角變大時,影響增大。
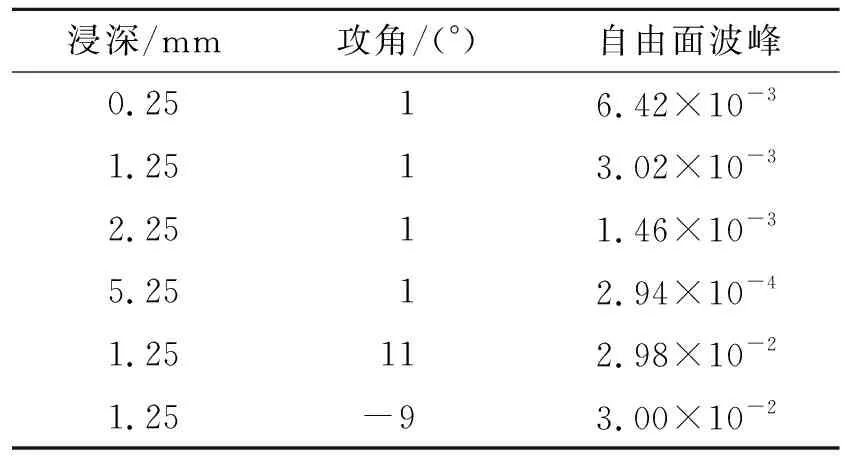
表1 不同浸深和尾渦角度的自由面波峰值
表2表明,當水翼浸深增大時,對升力影響不大;當攻角增大時,升力增大;當攻角為負時,升力也為負。
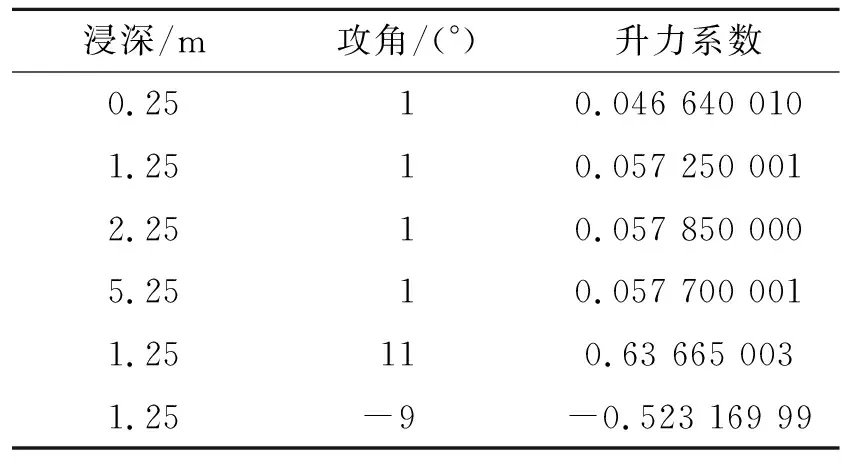
表2 不同浸深和尾渦角度的升力系數
3.2 算例二數值計算及實驗
使用NACA4412水翼作為計算算例,對于不同水翼浸深和功角得出的計算結果與實驗結果進行比較。證明系統的正確性。
圖5是實驗模型中水翼和建模完成后的示意圖,工況參數見4.1。
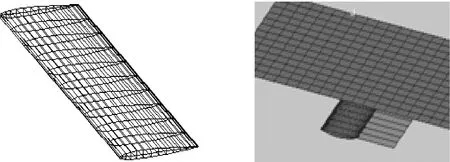
圖5 試驗水翼及自動建模后模型示意
弦長c弗勞德數Frc越小,即來流速度越小。
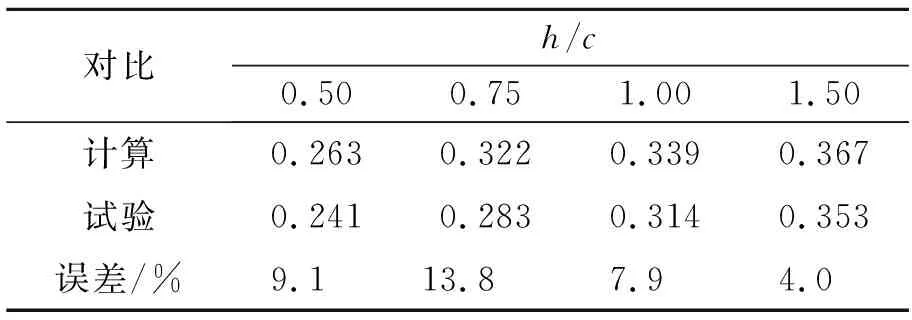
表3 水翼功角0°時不同浸深的實驗和計算對比
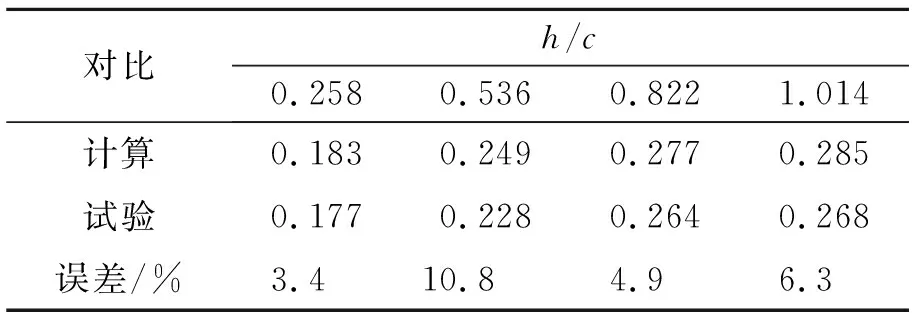
表4 水翼功角4°時不同浸深的實驗和計算對比
系統經過求解器計算,可以生成一個*.plt的文件,h/c=0.5,Frc分別為0.5、1.0、2.5和4.5時用TecPlot查看的結果見圖6。

a) Frc=0.5

b) Frc=1.0

c) Frc=2.5

d) Frc=2.5
4 總結
文中依據水翼升力面理論計算方法,并對已有的水翼特性經驗公式進行整理,在MSC.Patran平臺上實現了水翼升力求解的有限元方法,根據水翼模型和流場計算域特征進行參數化建模,改變水翼浸深和尾渦角度得到一系列的實驗結果,通過結果與已有規律的對比,發現是一致的,證明了使用該方法的正確性。工程算例的數值計算與試驗結果對比表明該方法可以對水翼升力及其分布進行預報。對產品的快速設計和優化都有重要的參考價值。
[1] 馬愛軍,周傳月,王 旭.Patran和Nastran有限元分析專業教程[M].北京:清華大學出版社,2005.
[2] 趙發明.水翼船水動力性能設計預報軟件包[D].無錫:中國船舶科學研究中心,2000.
[3] 張培培,陶 華,顧小鋒.CAD/CAE集成中參數化有限元建模的研究[J].現代制造工程,2006(9):2-3.
[4] Grose J G, Marx D A, Kranz M, et al.用MSC.Patran進行參數化設計與分析——一種新功能[C].MSC.Software Corp,MSC.Software中國解決方案論壇,2000:583-589.
[5] 朱 鳴,段云嶺.讀取MSC.Patran數據庫中的有限元信息[C].清華大學水利系,MSC.Software中國解決方案論壇,2000:599-602.

