AVL Excite在動力總成懸置系統設計中的應用

，

(武漢理工大學 能源與動力工程學院， 武漢 430063)

影響發動機懸置系統隔振效果的因素很多，各影響因素之間的關系比較復雜，對動力總成懸置系統的合理設計很關鍵，必須反復地進行理論分析和實驗驗證，要消耗大量的物力和時間。若能借助比較成熟的軟件對發動機的工作過程進行仿真模擬，可以提高設計效率。AVL Excite是奧地利李斯特內燃機及測試設備公司開發的一款發動機動力學仿真軟件，它綜合了有限元和多體動力學的分析原理，并結合了李斯特公司在發動機設計方面積累的豐富經驗。目前國內還未見采用AVL Excite(以下簡稱Excite)進行懸置系統設計的相關文獻報道，本文介紹利用Excite從多組發動機懸置軟墊中選擇出最佳組合。

1 發動機基本技術參數

研究對象選擇德國道依茨公司生產的BF6M1013ECP型柴油機，主要技術參數見表1。

表1 發動機主要技術參數

直列六缸機主要受氣缸內氣體壓力和往復慣性質量引起的傾覆力矩以及內力矩的作用。BF6M1013ECP型柴油機受到的最低頻率的擾動力為內力矩，其頻率為10 Hz[1]。

2 發動機相關參數

建立如圖1所示的坐標系。

坐標系原點位于質心處，x軸平行于曲軸指向自由端。發動機質量慣量和質心位置等基本參數與懸置系統的動態特性關系密切。動力總成總質量1 113 kg(用磅秤測出)，質心位置通過懸吊法測出，慣性參數通過扭擺法測出，分別見表2～4[2]。

圖1 發動機懸置四點支承系統

表2 動力總成的質心位置 mm

表3 動力總成的慣性參數 kg·m2

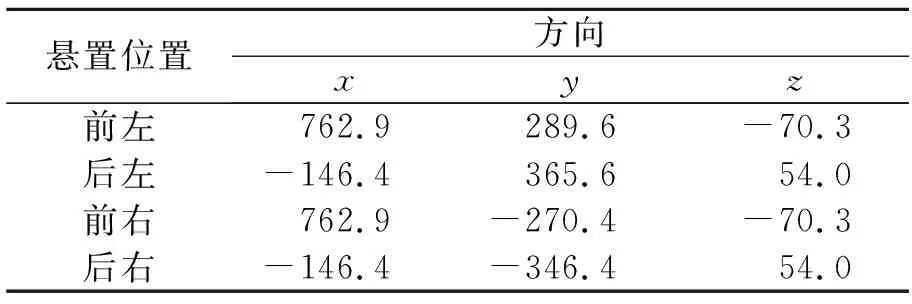
表4 懸置的布置位置 mm

3 懸置組合方案

有三種懸置元件的剛度組合方案可供選擇，見表5。

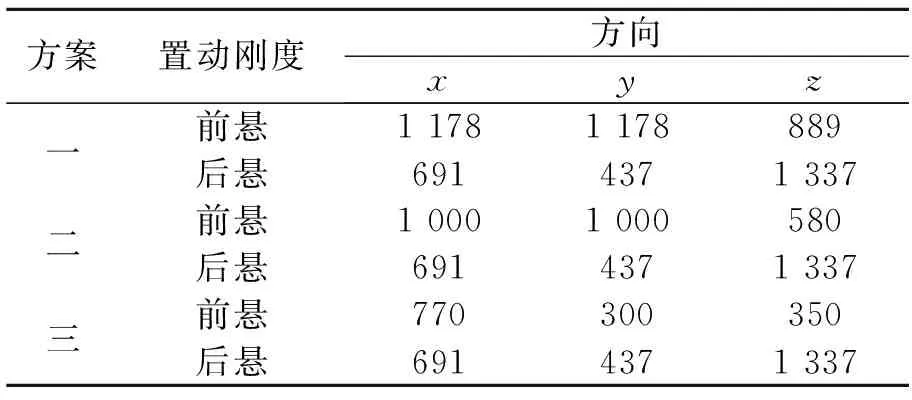
表5 組合剛度 N/mm

4 發動機懸置系統固有特性分析

利用上述各種參數可以得到質量矩陣和剛度矩陣，從而建立發動機懸置系統的運動特性方程，求解可以獲得懸置系統的固有頻率[3]。

發動機可以看作一個空間六自由度剛體，因此懸置系統存在六個剛體運動模態，分別是沿x軸、y軸、z軸的平移運動和繞x軸、繞y軸和繞z軸的旋轉運動，各個振動模態之間不是相互獨立的，而是互相耦合的，這種耦合的存在會增大發生共振的可能性，惡化發動機的振動狀況，因此通過調整設計參數，盡量降低各個振動模態之間的耦合程度是懸置系統設計的主要方向[4]。

發動機懸置系統各個模態之間的耦合程度可用能量耦合因子ηi來衡量，其表達式如下：

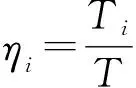
i=x,y,z,θx,θy,θz(1)

式中，T——某階模態的總能量

Ti——該階模態下i方向的能量，

mkl——質量矩陣第k行第l列元素;

Φj——階模態下對應的振型向量；

(Φj)k、(Φj)l——Φj第k及第l個元素。

ηi越大表明i方向的運動與其它運動之間的解耦程度越高，一般將ηi大于0.9視為完全解耦。

表6～8列出了三種不同懸置系統的固有頻率和能量耦合狀況[2]。

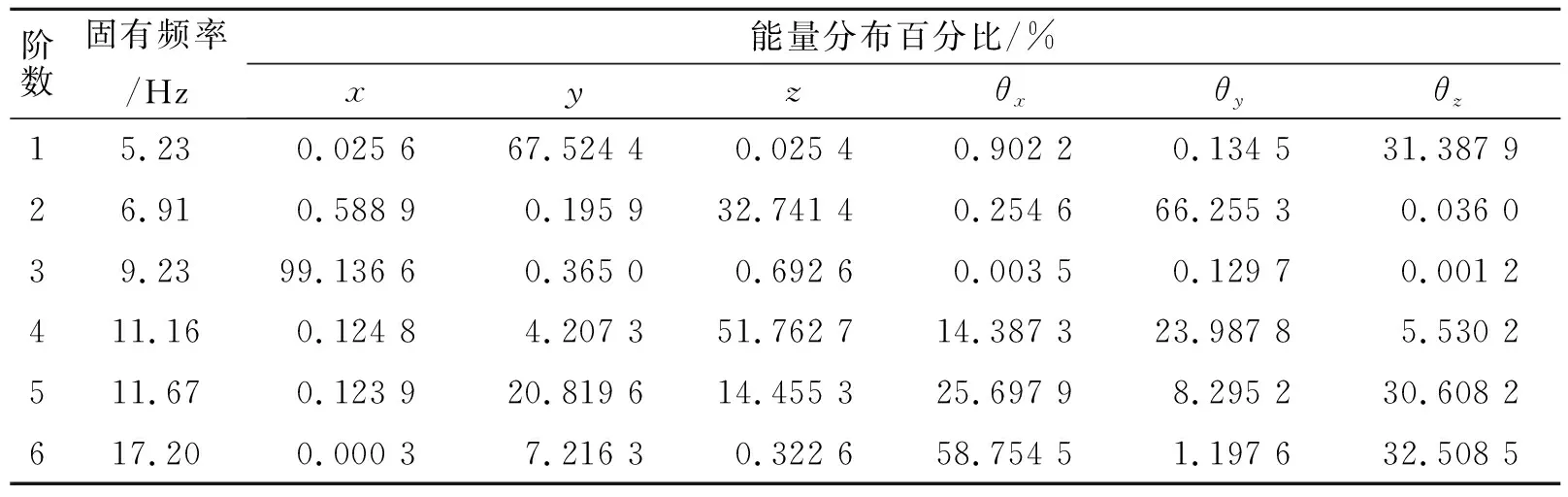
表6 方案一的能量耦合矩陣

表7 方案二的能量耦合矩陣

表8 方案三的能量耦合矩陣

比較各方案的固有頻率可知，方案三對應各階固有頻率比方案一和方案二對應各階固有頻率都要小，固有頻率越小意味著離共振區越遠，也更有利于減小發動機的振動。比較采用各方案后的能量耦合關系可以發現方案三繞x軸旋轉方向的解耦程度最高，達到了91.8%；方案二其次，為61.9%；方案一最低，為58.8%。而繞x軸旋轉方向是直列式六缸機的主要受力方向，該方向的解耦程度越高對降低發動機振動越有利。因此可以確定方案三為最佳方案，方案二其次。

5 Excite仿真

不考慮基礎的彈性效應，設基礎為剛體。輸入的外界載荷參數為氣缸壓力曲線。在Excite中建立模型。

模型中，機體和曲軸采用剛體模塊，用質心位置、質量和轉動慣量來表征發動機的固有特性。支承模塊采用非線性單元，用來表征剛度和阻尼隨位移非線性變化的關系。

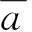
(2)

式中：a(t)——懸置點處振動加速度時間歷程，m/s2；

T——采樣時間，s；

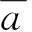
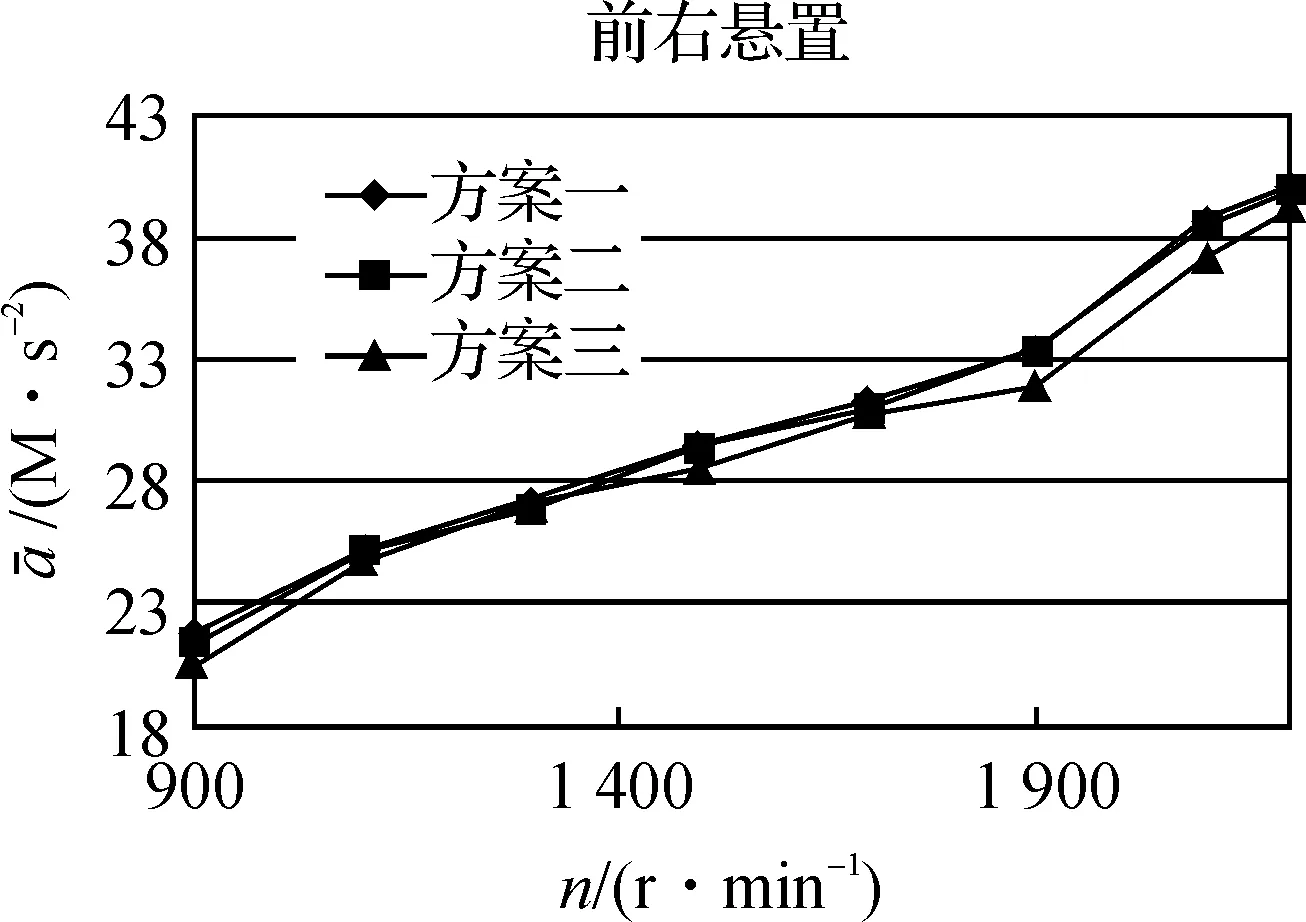
仿真結果見圖2。

由于隨著轉速的提高，缸內氣體作用力和往復慣性力呈增大的趨勢，因此從整體上看，加速度均方根值曲線呈上揚的趨勢。從仿真結果看，方案三對各懸置剛度配置最為合理，對改善整機振動狀況效果最好，方案二其次。

b)

c)

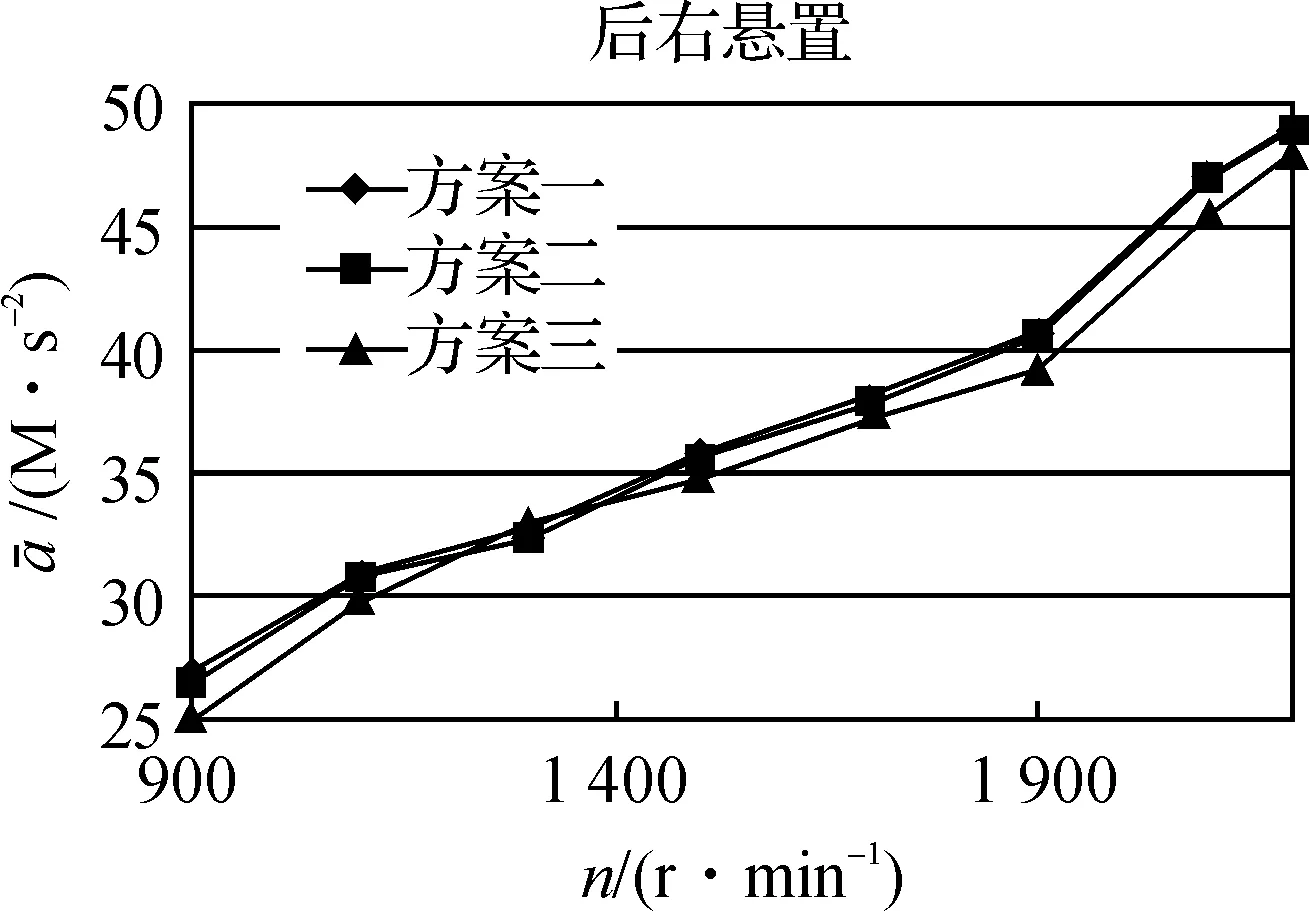
d)圖2 仿真結果

6 實驗測試

由于實際發動機懸置的上下支架均為彈性，因此采用加速度傳感器分別布置在前后四個懸置上、下八個測點處測取不同轉速工況下的z向加速度信號，見圖3。這里用振動傳遞率L來表征發動機懸置系統隔振效果的好壞。

(3)

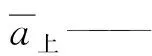
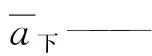
L越小表明隔振效果越好[2]。

從整個轉速范圍內看出，方案三隔振效果最好，方案二其次，方案一效果最差。

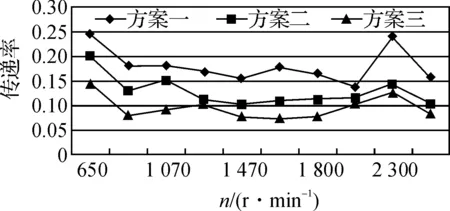
a)

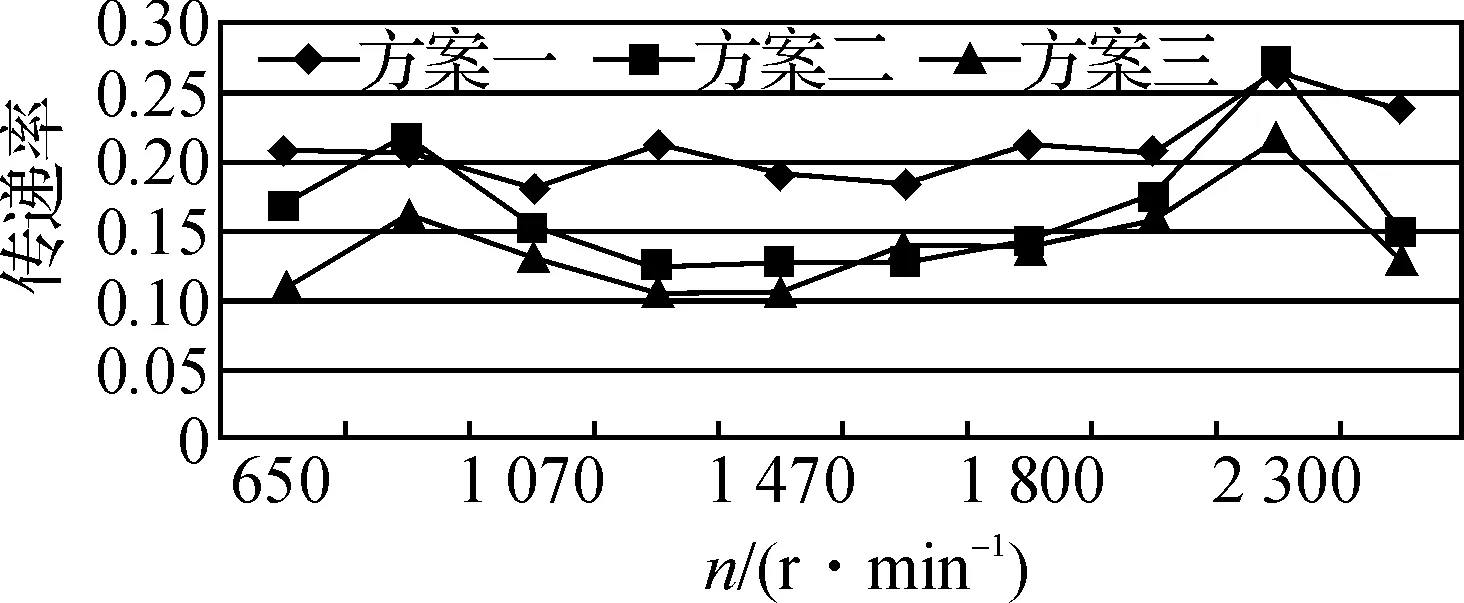
b)

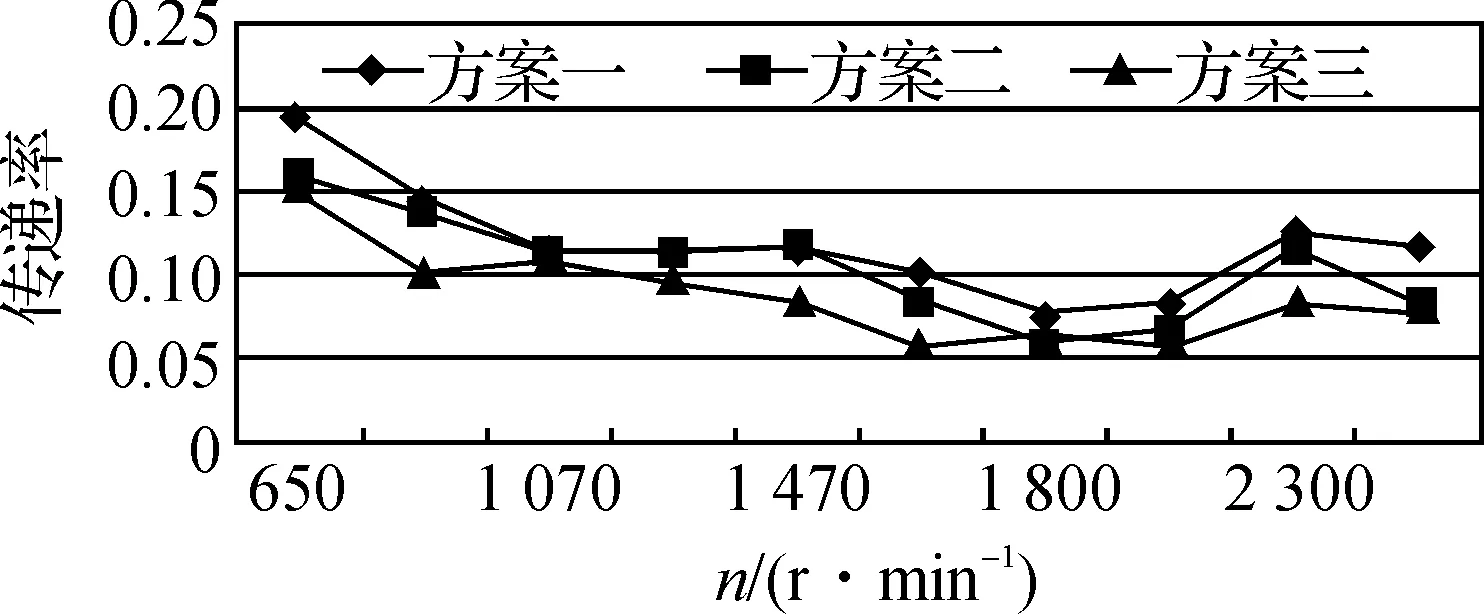
c)

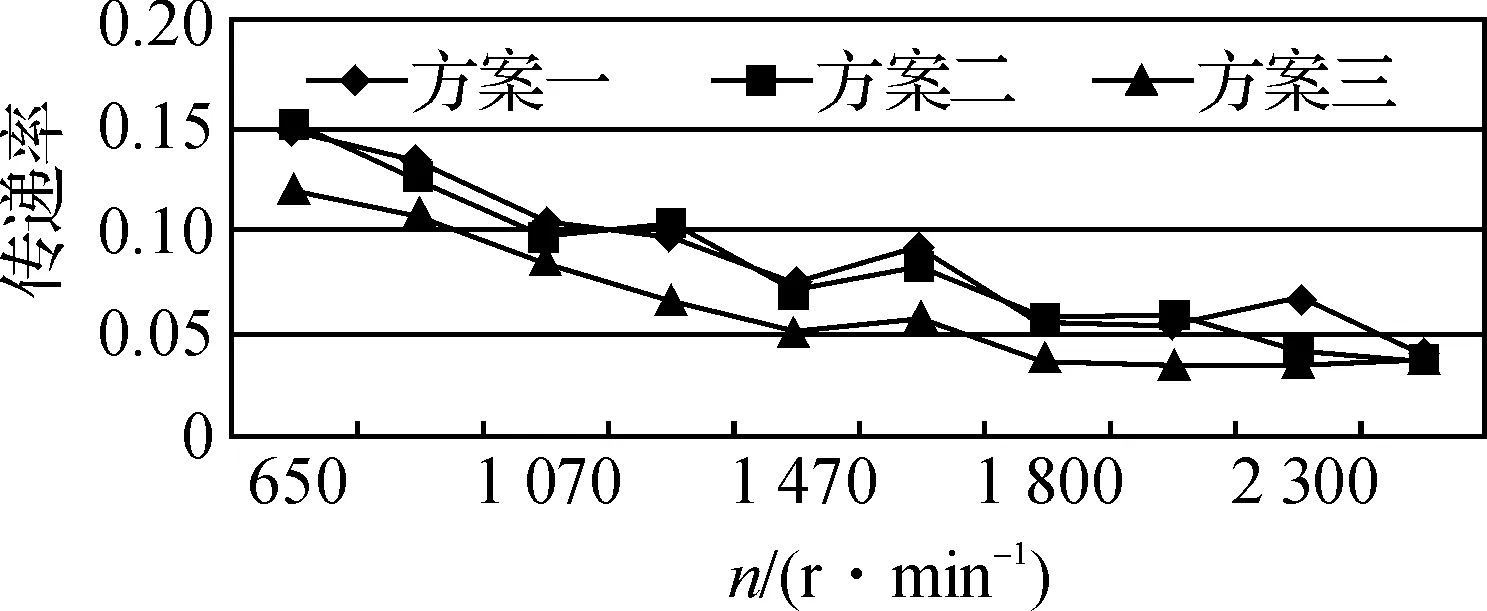
d)圖3 實驗結果

7 結束語

1) 通過仿真分析得到的結論與能量解耦理論和實驗測試結果得出的結論是一致的，由此可以確信對于發動機置系統設計Excite是一個有力的工具。雖然主要將Excite用于懸置組合方案的選擇，實際上也可用于其它懸置設計的場合如懸置系統參數的優化設計等，通過Excite仿真能夠方便進行分析和模擬，起到部分代替實驗的作用，從而降低實驗成本，縮短研發周期。

2) 主要探討了Excite仿真結果的變化趨勢，對結果的精度未予關注，只考慮了部分主要因素的影響，因此對Excite模型進行了大量的簡化，如假設機體、曲軸和基礎為剛體，忽略了懸置剛度阻尼的頻變和幅變特性，沒有考慮氣體壓力以外其它的可能對發動機振動有影響的作用力如配氣機構的作用力，若要得到比較精確的結果，需建立發動機機體和曲軸的有限元模型，并對懸置的特性進行精確的測量。當然，分析時間也會延長，所以必須綜合進行權衡。

[1] 吳炎庭，袁衛平.內燃機噪聲振動控制[M].北京：機械工業出版社，2005.

[2] 趙彤航.CA1261 汽車發動機懸置系統隔振的研究[D].長春：吉林大學，2002.

[3] 方錫邦,汪 佳.轎車動力總成懸置系統三維動力學模型的建立及優化[J].阜陽師范學院學報：自然科學版，2004，21(2)：45-48，56.

[4] 林峰印.引擎怠速狀態隔振系統配置最佳化設計[J].車輛研測咨詢，2006(1)：25.