高速單體船推進系統參數辨識方法研究

， ， ，

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003)

與船舶推進運動相關的參數分為兩大部分，最為重要的是螺旋槳的一系列參數，其次是伴流分數和推力減額。現階段實船大多數選用系列槳，即在選定好槳的同時已經能通過查圖譜得到該槳型的敞水性能曲線。但是在加工螺旋槳時因施工影響，大部分槳型與其所對應的理想槳型存在著一定的誤差，這就造成了敞水性能與圖譜有差別。

由于船舶航行時工況的不穩定以及船尾螺旋槳的空泡效應使得船舶實際的螺旋槳敞水性能和理論值有比較明顯的誤差。

考慮船舶運行數年后型線發生變化以及海況的影響，船舶在運行過程中的船身效率和相對旋轉效率都是不確定的。因此通過測得船舶在運行時的速度和主機功率來辨識出船舶推進系統的各參數是比較有意義的。

現階段系統辨識在船舶運動模式上的應用主要是集中在船舶的操縱性運動模式上。[1-2]本文將系統辨識應用到船舶推進系統中，通過仿真得到輸入和輸出量辨識出推進系統中的各待辨識參數包括伴流分數，推力減額以及螺旋槳的一系列水動力參數。在辨識的算法選擇中用遺傳算法的優化方法作為辨識方法。

1 數學模型

1.1 高速單體船的阻力

先期工作已經完成，基于MatLab的Simulink工具箱編寫高速單體船推進系統的仿真實驗平臺[3]。利用該平臺，可以在不通過實船與模型試驗的情況下，得到有關的數據參量，為試驗數據處理辨識方法研究提供便利。

利用該仿真平臺，讀取高速單體船在某一航速下的主機功率的值。利用下式可以得到船舶航行的阻力R。

(1)

式中：Pe——有效功率；

Ps——軸功率；

ηs——軸傳送效率，取0.98；

ηr——相對旋轉效率；

ηh——船身效率；

ηo——螺旋槳敞水效率。

對給定的螺旋槳而言，推力系數、轉矩系數和敞水效率僅與進速系數有關，因此有：

(2)

(3)

式中：kt——推力系數；

kq——轉矩系數；

T——螺旋槳推力；

Q——螺旋槳轉矩；

J——進速系數；

t——推力減額；

W——伴流分數。

將式(2)和(3)代入式(1)并整理得：

(4)

即將阻力化作關于kq,kt,ηr的函數。

1.2 高速單體船推進系統

在船舶的推力系統中主要的物理量有

推力T，轉矩Q，敞水效率ηo，有效推力Tp進速Va，進速系數J。

由于在很多情況下，可以將kt-J以及10kq-J的關系曲線看作是兩個二次函數的擬合[2]。即：

kt=a0J2+a1J+a2

(5)

10kq=b0J2+b1J+b2

(6)

可見在螺旋槳確定后kt-J和10kq-J都是確定的，即式(5)、(6)中的ai,bi(i=0,1,2)都是定值。

1.3 數學模型

為進行推進系數的辨識，選取船舶在勻加速直線的狀態作為研究對象，根據平動方程有：

zp(1-t)T-R=1.1△a

(7)

式中：a——加速度,常數；

△——排水量，常數。

將式(7)中各量分解

(8)

式中：zp為螺旋槳個數。

將上kt各式帶入式(8)，測取一系列的航速時的數值，令：

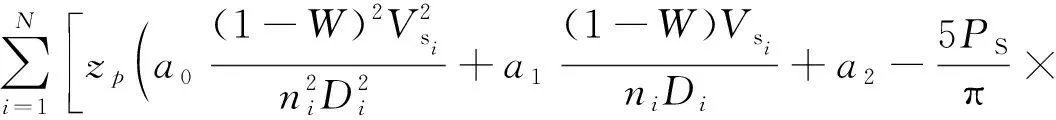
(9)

辨識模型中輸入量有：n,Vs,Ps,D,△,a,zp；輸出量即辨識參量為：ai,bi,W,t,ηr(i=0,1,2)。

2 辨識方法

由于在辨識的過程中其各待辨識參數都是常量，即與時間無關，采取離線辨識即可。筆者在辨識中采用優化的方法，通過給出各設計變量的范圍選用適合的優化方法得到需要辨識的各參數。優化的三要素為設計變量、目標函數和約束條件。

2.1 設計變量

選用上面9個輸出量作為設計變量：表示kt-J和10kq-J曲線的6個系數a0、a1、a2、b0、b1、b2還有ηr，W和t。

將這9個設計變量用一個向量X來表示：

XT={a0,a1,a2,b0,b1,b2,W,t,ηr}

2.2 目標函數

通過仿真平臺，取得在一系列的進速系數下船舶在穩定前進時的Vs、a、n、Ps，分別記此時的數據為Vsi、ai、ni、Psi，則優化目標函數的表達式為(9)。

2.3 約束條件

對這個目標函數的優化約束條件主要為轉矩的等式約束和設計變量上下限的約束。

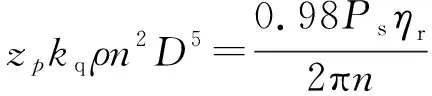
(10)

包括a0,a1,a2,b0,b1,b2,(1-W),(1-t)

一般取： 0.05≤W≤0.4；

0.05≤t≤0.15；

0.9≤ηr≤1.1。

根據二次曲線的意義一般取：

-0.50≤a0≤-0.05；

-0.50≤a1≤-0.05；

0.30≤a2≤0.80；

-0.50≤b0≤-0.05；

-0.50≤b1≤-0.05；

0.30≤b2≤1.5。

2.4 優化方法

在辨識此系統的各系統參數的過程中，由于遺傳算法[4-5]作為優化算法在全局優化上有著比較明顯的優勢而且原理較為簡單比較容易實現，因此選用遺傳算法作為優化方法。

在VC++界面中編寫適應度函數和主程序。編寫主程序時將各個設計變量的上下限，選擇方法，種群數，遺傳的代數等確定。

基因：x1,x2,x3,x4,x5,x6,x7,x8,x9對應優化數學模型中的a0,a1,a2,b0,b1,b2,W,t,ηr；

染色體：{x1,x2,x3,x4.x5,x6,x7,x8,x9}的二進制編碼的字符串，即對應于設計變量的組合；

種群數：這里的設計變量有限，選擇種群數500。實際效果被證明很好。

遺傳代數：選擇3 000代。

2.5 懲罰策略

將約束條件加入到目標函數當中，根據經驗懲罰因子[5-6]取10。并在適應值函數中選用乘法的形式作為懲罰項。

3 算例以及分析

本論文選用1 000 t的高速單體船在20個穩定航速變化下的仿真模型作為研究的對象，分別在Simulink下讀取各參量的值，再利用遺傳算法對該模型進行系統辨識，從而用辨識出的kt-J曲線和10kq-J與仿真模型下的各點做比較。

其中高速單體船的五葉螺旋槳P/D=0.85，Ae/Ao=0.6，遺傳算法中選種群為500，代數為3 000代，交叉率為0.8,變異率為0.05。可以得到最大的適應值函數的值為-0.009 677，其中各代辨識參數值為：

a0=-0.153 3，a1=-0.275 5，a2=0.401 3，

b0=-0.214 9，b1=-0.250 6，b2=0.496 1，

W=0.065 3，t=0.081 9，ηr=0.978 2

根據上面的數據用二次擬合出的曲線見圖1。

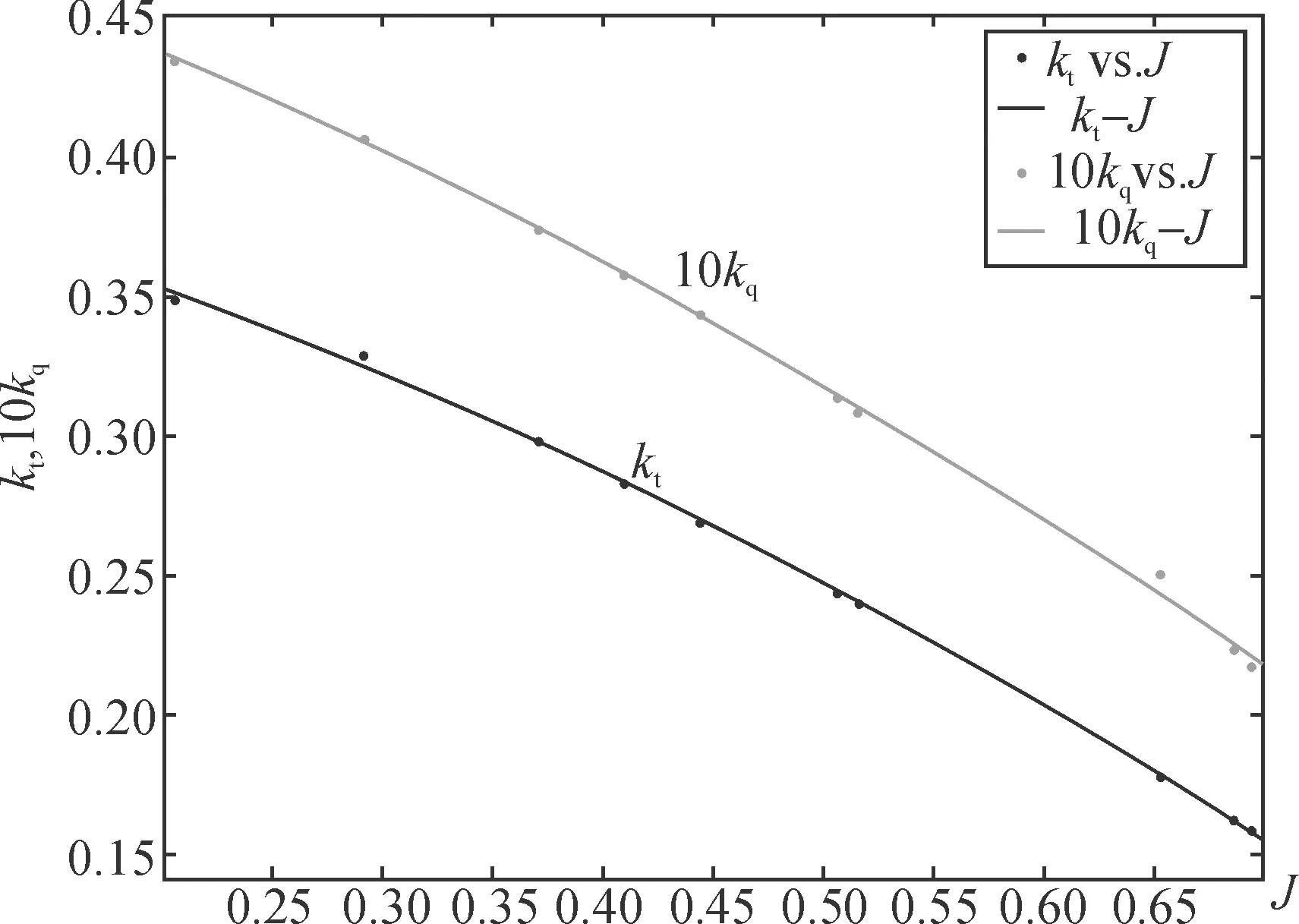
圖1 螺旋槳推力系數和轉矩系數曲

從上面的圖中，可以看出由二次函數擬合出的kt-J和10kq-J的曲線可以比較近似的反映出螺旋槳推進系數和進速系數的關系。圖中的10個點分別是用仿真的方法取得的J在0.2～0.8范圍內時kt和10kq的數值。

除了有些點有明顯誤差外其余的點吻合都不錯。可以看出如果在能取得足夠多航行實驗的情況下可以做到擬合出的kt-J和10kq-J曲線能夠滿足設計者的要求。由此證明了該方法用于高速單體船推進系數的辨識是可行的。

[1] 樂美龍.船舶操縱性預報與港航操縱運動仿真[M].上海：上海交通大學出版社, 2004.

[2] 賈欣樂, 楊鹽生.船舶運動數學模型機理建模與辨識建模[M].大連：大連海事大學出版社, 1999.

[3] 王 義, 董 亮, 楊松林.基于在線仿真的穿浪船推進智能控制及系統優化研究[J].江蘇科技大學學報：自然科學版, 2006,20(1):11-15.

[4] 玄光男, 程潤偉.遺傳算法與工程設計[M].北京：科學出版社, 2000.

[5] 米凱利維茨 Z.演化程序——遺傳算法與數據編碼的結合[M].北京：科學出版社, 2000.

[6] 張火明, 楊松林.遺傳算法在船舶航行性能優化中的懲罰策略[J].華東船舶工業學院學報：自然科學版, 2001,15(4):1-5.