幾何畫板與初中數學教學整合的探索嘗試

趙玉霞

1 利用幾何畫板輔助教師講授基礎知識,幫助學生理解基本概念

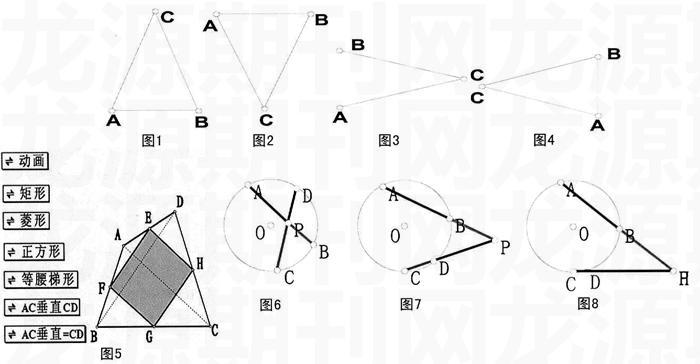
在幾何教學中,正確地教會學生識別幾何圖形,教懂學生作圖,成為突破幾何教學難的契機。例如,為讓學生正確理解等腰三角形的概念,并能在不同的情況下正確識別之,繪制具有代表性的底在水平線上和在垂直線上的等腰三角形和一般三角形(圖1～圖4)讓學生觀察、分辨、識別。由于用幾何畫板操作起來很容易,因此,用以引導學生理解等腰三角形的定義,把握概念的實質,是很方便的。此外,采取“移動頂點或對原圖進行變換”等方式很容易對繪制好的圖形進行處理,因而可以讓學生對處于不同位置上的等腰三角形都得到直觀的認識和了解。這種利用幾何畫板的基本功能來表現概念的“形態”的做法能有效加深學生對概念的理解和認識,避免或減少學生因圖形的問題而出現錯誤。

這樣的利用幾何畫板輔助教學,能加強學生的記憶和理解,為學生更好地學習提供幫助。

2 利用幾何畫板動態展示教學內容或數學問題,把抽象的數學教學變得形象、直觀

動態展示教學內容或數學問題,能夠化抽象為具體,化具體為形象,使教學更加直觀、生動,有利于激發學生的學習興趣,增強教學的趣味性。如對“四邊形各邊中點所圍成的四邊形是特殊的四邊形,且與原四邊形對角線有一定關系”這一問題的理解,內容比較多,教師可用幾何畫板軟件制作圖5所示的動畫演示效果:學生對四邊形ABCD的變化過程中四邊形EFGH的特征能直觀感受到,并且加深印象。

3 利用幾何畫板搭建驗證問題和揭示問題本質的技術平臺

3.1 為學生驗證問題搭建技術平臺,使幾何畫板成為“數學實驗室”有些數學問題由于本身的抽象性和推理的復雜性,讓人花費很多時間都未能證明出來,此時產生對問題的疑義并對問題真實性進行驗證是一種極為可能并想去做的事。如學生證明:“三角形中,如果有兩個角的平分線相等,則這個三角形是等腰三角形。”由于該題的證明思路很不容易被找到,學生嘗試多種方法均證不出來時,提出“老師,你讓我們證明的題目是正確的嗎”這樣的問題。筆者提示學生用幾何畫板對題目進行驗證,通過實際操作,證實題目沒有問題,學生重新思考證明方法。

3.2 揭示知識之間的內在本質,為學生體驗知識之間的關系提供“活動場”靜態的圖形、圖像使原本相互聯系的知識割裂開來,失去知識之間的內在聯系,會使學生只注意事物的局部而忽視整體。幾何畫板能動態地展示問題的特點,可以克服靜態圖形的這一缺陷。

4 利用幾何畫板給學生提供猜想和探索的技術環境

如學習了“相交弦定理”后,教師可以這樣提出問題,啟發學生去進行探索:“如圖6所示,根據相交弦定理,我們知道PA·PB=PC·PD。如果P點在☉0外,PA·PB=PC·PD這個結論還成立嗎?特別地,如果P點在過A、B、C、D中某一點的切線上時,結論又怎樣?”

此問題的探索大致可以按4個步驟進行。1)測量PA、PB、PC、PD的值,并計算PA·PB,PC·PD;2)用鼠標將P點從圓內拖到圓外(圖7);3)觀察PA·PB,PC·PD的值的變化情況,仔細查看當P點在圓外變動時變化了的PA·PB,PC·PD的值是否相等;4)得到結論。

對于切線位置,如圖8所示,可以過某一點(如C點)作圓的一條切線(CM),在該切線上任取一點H(H點最好不與C點重合);用選擇工具選擇P點,按住Shift鍵后再選H點,使兩點都被選中;用鼠標選擇“編輯”下的“操作類按鈕”下的“移動”命令,為從P點移動到H點設置一個運動按鈕;當雙擊按鈕時,P會從它的當前位置移動到H點,并使P、H兩點重合;通過觀察PA·PB,PC·PD的值,可確立兩者的值的關系,得到結論。■

(作者單位:山東省淄博市臨淄區辛店大武學校)