低年級數(shù)學(xué)學(xué)習(xí)過程中的錯誤原因例析

朱　宇

這是一些屢屢出現(xiàn)的錯誤：44-19=35，36×2=82，29÷3=8……5，如此等等。我們在痛心疾首之余，往往會疾言厲色地批評這些錯誤的小主人“太粗心”。由于低年級兒童的感知具有籠統(tǒng)、不精確的特征，因此在數(shù)學(xué)學(xué)習(xí)過程中經(jīng)常出現(xiàn)這些“低級錯誤”。這些“低級錯誤”真的可以用“粗心”一言以蔽之嗎？或者說，我們真的可以把產(chǎn)生這些錯誤的原因全部諉過于學(xué)生嗎？

在此，筆者試從兒童數(shù)學(xué)學(xué)習(xí)的特點，結(jié)合平時的教學(xué)實踐，對“粗心”背后的原因向自己，也向廣大的數(shù)學(xué)教師叩問——

一、 學(xué)生存在學(xué)習(xí)障礙嗎

1.言語障礙

對低年級學(xué)生而言，閱讀理解能力是解決數(shù)學(xué)問題的必要前提。小學(xué)數(shù)學(xué)應(yīng)用題中的詞匯有些是數(shù)學(xué)中的專門術(shù)語，有些則是生活中的日常用語。因此，指導(dǎo)學(xué)生準(zhǔn)確理解這些詞匯的內(nèi)涵是正確理解問題的前提。

例如，有這樣一道圖文應(yīng)用題：圖書室原來有500本故事書，1班：我們班要借200本；2班：我們班要還150本。現(xiàn)在圖書室有多少本故事書？

這樣一道加減混合的應(yīng)用題（500-200+150），許多學(xué)生筆下列出的卻是連減算式：500-200-150,問及緣由，著實令人哭笑不得：原來，二年級的學(xué)生還不能準(zhǔn)確地掌握“還”字的兩種讀音，把題目中的“要還（huán）”誤讀成“還（hái)要”,閱讀理解的偏差造成了解題思路的錯誤。

“‘60比15多得多，這句話還可以怎么說？”

“15比60少得少。”

學(xué)生由“多得多”想到“少得少”，其實并不是類推的結(jié)果。這其中生活經(jīng)驗的作用被忽視了。因為在后面的練習(xí)中，學(xué)生都很流利地說出“小紅比小明矮得多”、“小華的歲數(shù)比爺爺?shù)臍q數(shù)小得多”，完全沒有出現(xiàn)“矮得矮”、“小得小”這些不合規(guī)矩的說法。

數(shù)學(xué)上像這些約定俗成的表示方法，它們與生活聯(lián)系密切，如果在教學(xué)中不注意兩者的有機(jī)整合，也會給學(xué)生的語言表達(dá)帶來麻煩。

2.認(rèn)知欠缺

如果不是親耳聽到這位同學(xué)的解釋，我怎么也不會相信存在這樣的算法：

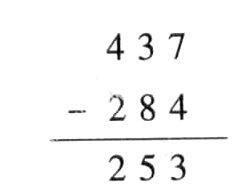
“個位上用7減4得3，十位上用8減3得5，百位上用4減2得2。”

“十位上為什么用8減3呢？”

“減法，就是用大的減去小的。”

天哪，如果不多問一個為什么，我們還會不厭其煩地告訴他和他的同學(xué)們：十位上3減8不夠，向百位借走了“1”，所以百位上應(yīng)該算3減2得1。

可他是這樣想的嗎？根本沒有！那么他怎么聽得進(jìn)我們的指導(dǎo)呢？正確的認(rèn)知建構(gòu)是避免錯誤的前提條件。

3.技能生疏

計算過程中失誤連連，根本原因在于學(xué)生沒有形成純熟的運(yùn)算技能。因此我們必須幫助學(xué)生實現(xiàn)計算行為的自動化。因為口算既是筆算、估算和簡算的基礎(chǔ)，也是計算能力的重要組成部分。在教學(xué)中，要做到每堂課上安排口算訓(xùn)練，形式可以包括聽算訓(xùn)練、視算訓(xùn)練、搶答、“開火車”等。此外，還應(yīng)該鼓勵學(xué)生參加必要的社會實踐，比如讓學(xué)生隨父母上街采購物品時，幫助家長口算價款。

因為低年級學(xué)生注意力差，所以，老師在課堂上一般不敢讓學(xué)生打開課本，認(rèn)為學(xué)生看了課本后，什么都知道了，就不會認(rèn)真聽課。實際上，由于低年級學(xué)生識字能力不強(qiáng)，對文字本身的含義理解不夠深刻，更加難以理解隱藏在文字背后的數(shù)學(xué)知識，難以領(lǐng)悟其中的密切聯(lián)系。因此，低年級老師更應(yīng)該指導(dǎo)學(xué)生有效地進(jìn)行數(shù)學(xué)閱讀，在閱讀的基礎(chǔ)上展開數(shù)學(xué)課堂教學(xué)。

二、 教師指導(dǎo)到位了嗎

1.怎能如此武斷

課上，一位學(xué)生計算36×2時把結(jié)果寫成了82。教師審視了其運(yùn)算豎式，指著這“顯而易見”的錯誤，諄諄告誡這位學(xué)生，以后不能如此粗心。該生雖說滿臉通紅，低著頭，口里卻小聲嘀咕著什么。看樣子，他挺有意見。

其時，筆者正在課堂上聽課，發(fā)現(xiàn)這位學(xué)生的書寫過程確實沒錯，于是悄悄地請他說說算理“二六十二，寫二進(jìn)一；三加一得四，二四得八”。

原來如此！我小聲地給他指出了他運(yùn)算順序上的錯誤之處，十位上應(yīng)先算2個3，再加上1，得7，結(jié)果是72。

學(xué)生在計算過程中發(fā)生的錯誤，確有粗心造成的，這涉及學(xué)習(xí)習(xí)慣與意志品質(zhì)的培養(yǎng)，這里且不提它。但是，更多的錯誤，卻各有其產(chǎn)生的原因，有的是因感知錯誤，導(dǎo)致法則出錯；有的是因舊知識的干擾，而產(chǎn)生的痕跡性錯誤；有的是因概念模糊而產(chǎn)生的錯誤。

我們常教育學(xué)生說：學(xué)習(xí)知識，不僅要知其然，更要知其所以然。那么，身為教師的我們，在對待學(xué)生計算中的錯誤時，又何嘗不應(yīng)如此呢？我們做教師的不僅要“明其錯”，更要“明其何以錯”，方能讓學(xué)生找到錯誤的根子，及時對癥下藥。否則，同樣的錯誤還會在同樣的地方繼續(xù)出現(xiàn)。

2.為何不能“坐下來看”

這是我的一次親身經(jīng)歷。

在 “觀察物體”這一課的課前，我給每桌準(zhǔn)備了三個同樣大小的正方體，讓他們課上拼擺、觀察。

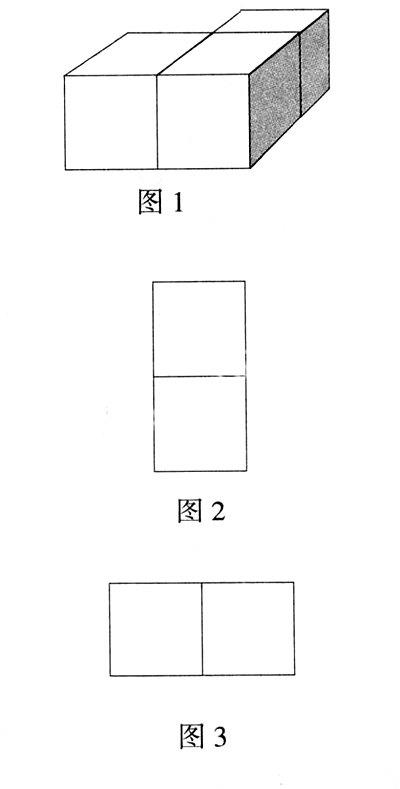
投影出示：如圖1，先擺一擺，再畫出從側(cè)面看到的圖形。

經(jīng)過一番操作、觀察，學(xué)生畫出的圖形讓我大吃一驚。

學(xué)生幾乎都畫出了圖2。

我很感意外：沒道理呀，從側(cè)面看到的圖形應(yīng)該是圖3。讓學(xué)生再觀察，但是學(xué)生仍然堅持自己的意見。

我剛準(zhǔn)備說些什么，這時，小紅同學(xué)大聲地對我說：“老師，你坐下來看！”

坐下來看？我邊琢磨著，邊來到小紅的座位旁邊。

小紅站起身，把她的座位讓給我。

位置太小，很不舒服，真難為他們了！與我視線的水平線相比，小正方體位置太低，我只得把頭向右側(cè)過去

我愣住了：眼前看到的分明是圖2，原先水平的兩個圖形竟然“立”了起來。

我一下子全明白了：從側(cè)面看，不等于側(cè)過頭看。側(cè)面與正面的區(qū)別不等于視角的“側(cè)”與“正”，而在于觀察者是否以身體正對物體的側(cè)面，視線是否垂直于物體的側(cè)面。

在我們成人的“想當(dāng)然”中，把“側(cè)面”“正面”理解得非常簡單，其實，這當(dāng)中的細(xì)節(jié)因素，如視角的調(diào)節(jié)、位置的移動等就很值得研究。然而，我只是籠統(tǒng)地提出一個“粗糙”的要求。

我們平時常常掛在嘴邊的一句話是：站在孩子們的角度看問題。然而，我們卻常常不自覺地以自己的思維替代孩子們的思考，以自己的主觀臆斷推測孩子們的客觀認(rèn)識。

3.不該“無心誤導(dǎo)”

課上，認(rèn)識完整時后，教者把分針撥到12過了一點點，這時時針自然也過了“8”，看著這時的鐘面，師生共同找到了表示這一時刻的方法——大約8時。以同樣的方法學(xué)生又認(rèn)識了“大約1時、10時”……

從“幾時”到“大約幾時”，似乎大功告成。然而，當(dāng)教師把分針撥到12左邊一點點時，指著時針（6不到一點）提問，學(xué)生的回答把教師嚇了一跳：小約6時。

竟然還有“小約”幾時。

是孩子們在信口胡言嗎？不是，他們錯誤答案的背后還有推理過程呢：既然分針過了12多一點叫大約幾時，那么，相應(yīng)地，分鐘不到12，當(dāng)然被稱為“小約幾時”了。

錯誤的緣起在于教師推介材料的不當(dāng)。須知，“大約幾時”是相對于整時出現(xiàn)的一個模糊概念，應(yīng)該包括“整時多一點”和“整時差一點”，兩者之間是并列關(guān)系，并無先后關(guān)系。材料呈現(xiàn)時機(jī)的不當(dāng)造成了學(xué)生認(rèn)知上的“先入為主”。

三、 你有長遠(yuǎn)的眼光嗎

1.提倡一次做對

犯錯后及時糾錯，這是對的。但總是做“事后諸葛亮”并不是明智之舉。我們應(yīng)要求學(xué)生一次做對。比如，要求學(xué)生對于所抄寫下來的題目都進(jìn)行認(rèn)真校對，細(xì)到數(shù)字、符號，不錯不漏。看清題目中的每一個數(shù)據(jù)和運(yùn)算符號，確定運(yùn)算順序，選擇合理的運(yùn)算方法。規(guī)范書寫，做到書寫工整、格式正確、字跡端正。另外，要教給他們驗算和估算的方法，并將驗算作為計算過程的一個重要環(huán)節(jié)進(jìn)行嚴(yán)格要求。

2.培養(yǎng)反思意識

對學(xué)習(xí)過程中表現(xiàn)出來的錯誤，我們不能簡單地下判斷，可以“將錯就錯”，要求學(xué)生觀察、分析，自行找出錯誤的原因，不僅“明其錯”，更要“明其何以錯”。很多時候，學(xué)生在探索過程中不一定都能獲得對錯誤的體驗，因此，作為處于主導(dǎo)地位的教師，有時可以巧設(shè)“陷阱”，讓學(xué)生于不經(jīng)意間“上當(dāng)”一回，從而有效地彌補(bǔ)探索過程中的體驗不足。在解決問題的過程中，我們還應(yīng)該經(jīng)常這樣問學(xué)生：想一想，你為什么沒有得到問題的答案？這個問題之所以沒能得到解決，主要原因在哪里？怎樣修改就可以了？