二項分布參數多層Bayes和E Bayes估計的性質
王建華,毛娟
(1.華中科技大學數學與統計學院,湖北武漢 430074;2.武漢理工大學理學院數學系,湖北武漢 430070)
二項分布參數多層Bayes和E Bayes估計的性質
王建華1,2,毛娟2
(1.華中科技大學數學與統計學院,湖北武漢 430074;2.武漢理工大學理學院數學系,湖北武漢 430070)
討論無失效數據下二項分布參數E Bayes估計和多層Bayes估計的性質,證明二項參數的多層Bayes估計和E Bayes估計漸近相等,且E Bayes估計值小于多層Bayes估計值.
二項分布;參數估計;E Bayes估計;多層Bayes估計
1 引言
在可靠性試驗中,對高可靠性產品進行定時截尾試驗,在規定的試驗時間內往往沒有樣品失效,獲得的數據為無失效數據.基于無失效數據的可靠性參數估計對高可靠性產品的可靠性研究具有重要的理論和應用價值[14].韓明博士對這一問題進行了系統的研究,所作專著《基于無失效數據的可靠性參數估計》是這一研究成果的總結.遺憾的是關于無失效數據的可靠性參數多層Bayes和E Bayes估計性質的三個命題(文[1]中命題2.1,命題3.1,命題6.1)未能給出數學證明,只給出數值算例說明.本文給出命題6.1的數學證明,其他命題的數學證明將另撰文給出.
設某產品的壽命分布類型是未知的,現從中隨機抽取n個樣品進行定時截尾試驗,若在截尾試驗時間段內有X個樣品失效,又產品的失效與否是相互獨立的,則X是一個服從二項分布的隨機變量,于是有
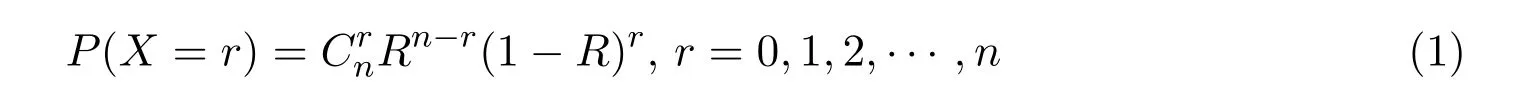
其中0<R<1,R為產品的可靠度.
這樣研究可靠度的非參數估計問題,就轉化為研究二項分布(1)中參數R的估計問題. 若R的先驗分布為Bata分布,其密度函數為
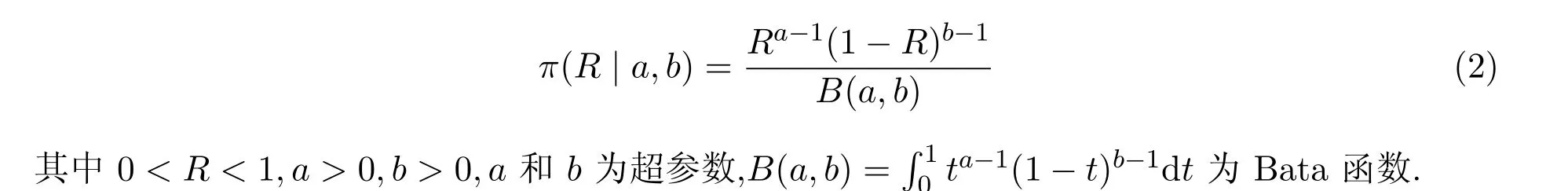
當0<b<1,a>1時,π(R|a,b)為R的單調增函數,滿足多層先驗分布增函數構造法要求.尾部越細的先驗分布會使Bayes估計的穩健性越差,因此在0<b<1時a不宜過大,設a的上界為c(c>1為常數).超參數a和b的取值范圍為區域D={(a,b)|1<a<c,0<b<1}. 設a的先驗分布為(1,c)上的均勻分布,b的先驗分布為(0,1)上的均勻分布,則在a和b獨立時,R的多層先驗密度函數為
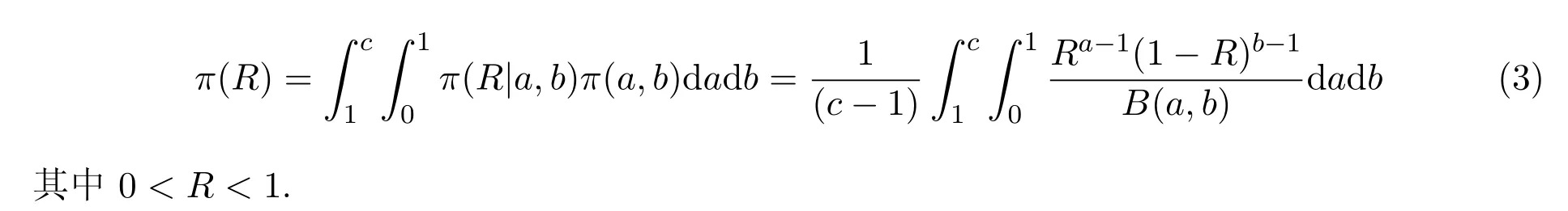
R的多層Bayes估計為[1]:
定理1對二項分布(1),在無失效數據情形下,若R的多層先驗密度函數由(3)給出,則在平方損失下,R的多層Bayes估計為
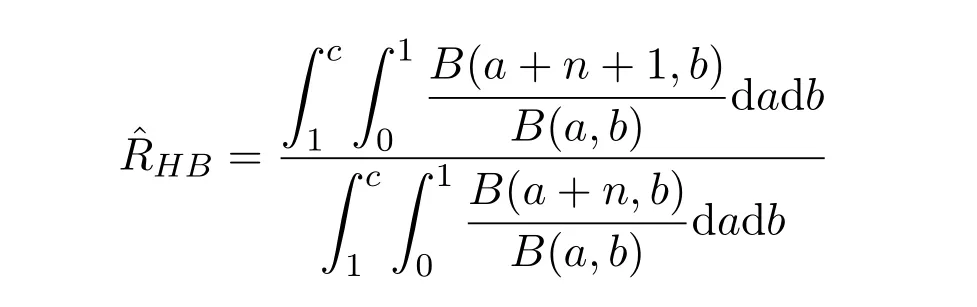
證明見文[1].
R的E Bayes估計為[1]:
定理2對二項分布(1),在無失效數據情形下,若R的先驗密度函數由(2)給出,則有(i)在平方損失下,R的Bayes估計為

2 引理
引理1n為正整數,a和b為實數,當0<b<1,a>1時,有
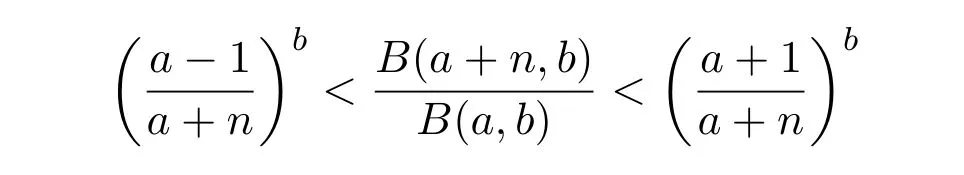
證明文[5]等證明了兩個Gamma函數比的不等式



3 定理的證明


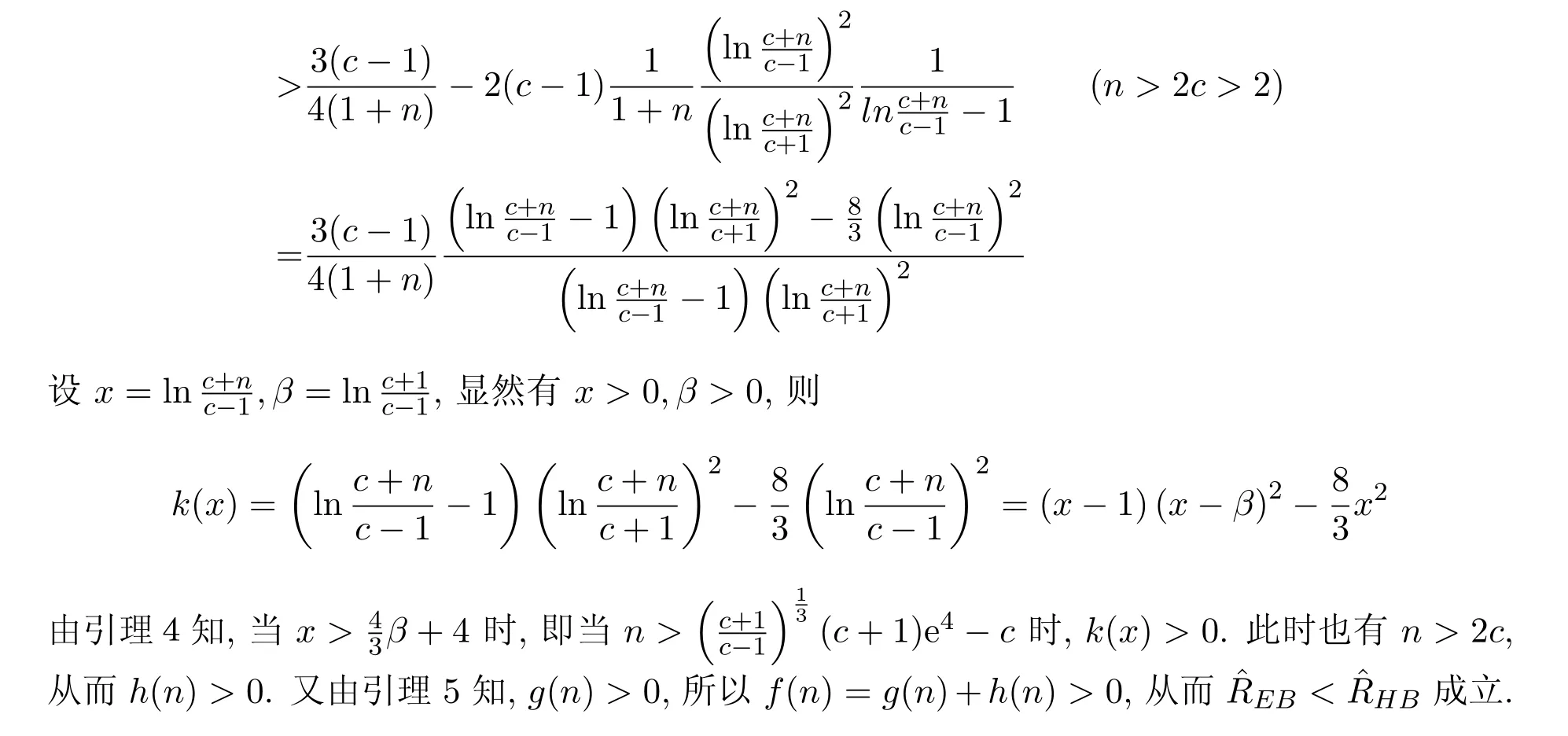
[1]韓明.基于無失效數據的可靠性參數估計[M].北京:中國統計出版社,2005.
[2]韓明.無失效數據情形可靠性參數的置信限[J].工程數學學報,2004,21(2):245-248.
[3]韓明.無失效數據情形可靠性參數的估計和調整[J].應用數學,2006,19(2):325-330.
[4]韓明.Pascal分布的參數估計[J].純粹數學與應用數學,2006,22(4):510-515.
[5]Elezovic N,Giordano C,Pecaric J.The best bounds in Gautschi’s inequality[J].M ath.Inequal.App l.,2000, 3(2):239-252.
The property of hierarchical Bayesian and E Bayesian estim ation of binom iald istribu tion’s param eter
WANG Jian-hua1,2,MAO Juan2
(1.School of Mathem atics and Statistics,Huazhong University of Science and Technology,Wuhan 430074,China;2.Department of Mathematics,College of Science,Wuhan University of Technology,Wuhan 430070,China)
This paper researches the asym ptotic property of hierarchical Bayesian and E Bayesian estim ation of binom ial distribution’s param eter in zero-failure data.This paper gives theMathem atical p roof of that the E Bayesian estimation of binom ial distribution’s parameter is asym ptotic equal to its hierarchical Bayesian estim ation and E Bayesian estim ation of binom ial distribution’s param eter is sm aller than its hierarchical Bayesian estim ation.
binom ial distribution,parameter estimation,E Bayesian estimation,hierarchical Bayesian estimation
O212.8
A
1008-5513(2009)02-0223-08
2007-10-25.
王建華(1965-),副教授.研究方向:應用概率統計與金融數學.
2000M SC:62F12,62F15

