模糊自動機的強連通性及群自動機

柏明強,莫智文

(四川師范大學數學與軟件科學學院,四川成都 610068)

模糊自動機的強連通性及群自動機

柏明強,莫智文

(四川師范大學數學與軟件科學學院,四川成都 610068)

為了更好地研究模糊自動機的結構和性質,采用代數的方法,在傳統的模糊有限狀態自動機的基礎上,通過定義狀態集合為代數群的自動機,討論了這一類自動機的連通性和正則性,這豐富了模糊自動機理論.

模糊自動機;群;強連通

1 前言

自動機理論是經典語言理論的一個重要內容,雖然其理論較為完善,但是研究成果仍然不斷涌現[12].自1965年Zadeh[3]提出了模糊集合的概念后,Wee[4]迅速將模糊集應用于自動機理論的研究,提出了模糊自動機.到現在為止,模糊自動機與模糊語言的研究成果也是十分豐富[59].強連通自動機是在自動機中的一種十分特殊的自動機,其不同于文[1-9]中的自動機,它要求狀態轉移必須是任意狀態之間均可進行.群自動機[1013]是在經典自動機基礎上擴展而成的.其將一般的狀態集拓展到代數群上.本文將群自動機和模糊集理論結合,提出了模糊群自動機的概念,這是模糊自動機理論的自然推廣.

設Σ是字母表,Σ?是Σ上的字符串集合,是一個么半群.設x=a1a2…an是一個字符串, 稱an…a2a1為x的逆像,記為xR.ε為空字符.

2 強連通模糊自動機

定義2.1[6]一個模糊有限自動機是一個五元組A=(Q,Σ,δ,I,F),其中Q是狀態的非空有限集,Σ是非空有限字母表,δ:Q×Σ→Q×[0,1]為狀態轉移函數,I?Q是初始狀態,F?Q是終止狀態集.

為了運算的方便,定義映射δ0為δ0(q,x)=p,當且僅當δ(q,x)=(p,μ),從而狀態轉移函數δ?可以擴展為從Q×Σ?到Q×[0,1]的映射,滿足:(1)?q∈Q,δ?(q,ε)=(q,1);(2)?q∈Q,x∈Σ,y∈Σ?,δ?(q,xy)=δ?(δ?(q,x),y),其中δ(q,xy)=(p,μ),δ(q,x)=(p1,μ1),δ(p1,y)= (p,μ2),μ=min{μ1,μ2}.

定義2.2設A=(Q,Σ,δ,I,F)是模糊有限自動機.如果?q,p∈Q,均存在x∈Σ?,使得δ(q,x)=(p,μ)且δ(p,xR)=(q,μ0),則稱A是模糊強連通自動機.

對于強連通自動機來說,其狀態轉移圖是連通圖,而且是完全圖.

定義2.3設A1=(Q1,Σ,δ1,I1,F1)和A2=(Q2,Σ,δ2,I2,F2)是模糊有限自動機,?是從Q1到Q2的映射.

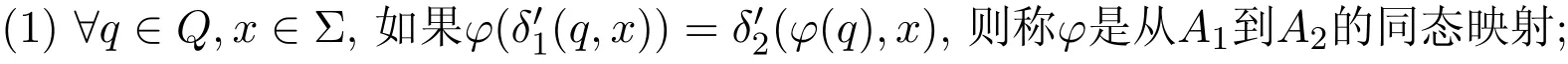
(2)如果?是從Q1到Q2的同態映射,且?是雙射,則稱?是從A1到A2的同構映射.

(3)如果A1和A2之間存在同構映射,則稱A1與A2相互同構,記為A1～=A2.

如果A1=A2,則稱A1與A2之間的同態和同構分別稱為自同態和自同構.記E(A)和G(A)分別為A上所有自同態和自同構構成的集合.顯然E(A)和G(A)分別為么半群和群.

性質2.1設A=(Q,Σ,δ,I,F)是一個強連通自動機.如果?,ζ∈G(A),且存在q0∈Q使得?(q0)=ζ(q0),則?q∈Q,均有?(q)=ζ(q).即如果?,ζ只要在某點的像相同,則?=ζ.

證明由于A是強連通的,?q∈Q,必存在x∈Σ?,使得δ(q0,x)=(q,μ),從而δ0(q0,x)=q,所以?(q)=?(δ0(q0,x))=δ0(?(q0),x)=δ0(ζ(q0),x)=ζ(δ0(q0,x))=ζ(q).

性質2.2設A=(Q,Σ,δ,I,F)是一個強連通自動機.則|G(A)|整除|Q|.

證明?p,q∈Q,如果存在?∈G(A),使得?(q)=p,則記p～q.顯然“～”是Q上的一個同余關系.記[q]={?(q)|?∈G(A)}.顯然[q]是含q且與q同余的一個類,稱為同余類.

定義2.4[9]設A=(Q,Σ,δ,I,F)是模糊有限自動機.如果?q∈Q,?x,y∈Σ?,均有δ(q,xy)= δ(q,yx),則稱A是可交換的.

交換性是代數中的一個重要性質,在自動機理論有很重要的地位.

如果一個交換的模糊有限自動機是強連通的,則稱其是完美自動機.

定理2.1設A=(Q,Σ,δ,I,F)是一個模糊有限自動機，則A是完美的充分必要條件是A是強連通的,|G(A)|=|Q|,且G(A)是可交換的.

從而?ζ=ζ?,即G(A)是可交換的.

4)由于A是完美的,所以A必是強連通的.

(充分性)欲證A是完美的,根據條件知,只需要證明A是可交換的即可.

?q∈Q,x∈Σ?,由?x(q)=δ0(q,x)定義的映射?x必是A上的自同構映射.

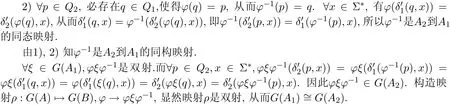
3 群矩陣型模糊自動機

定義3.1[13]設G是一個有限群.設G0=G∪{0},其上定義了兩個代數運算乘法“·”和加法“+”:

圖3 .1 A的狀態轉移圖

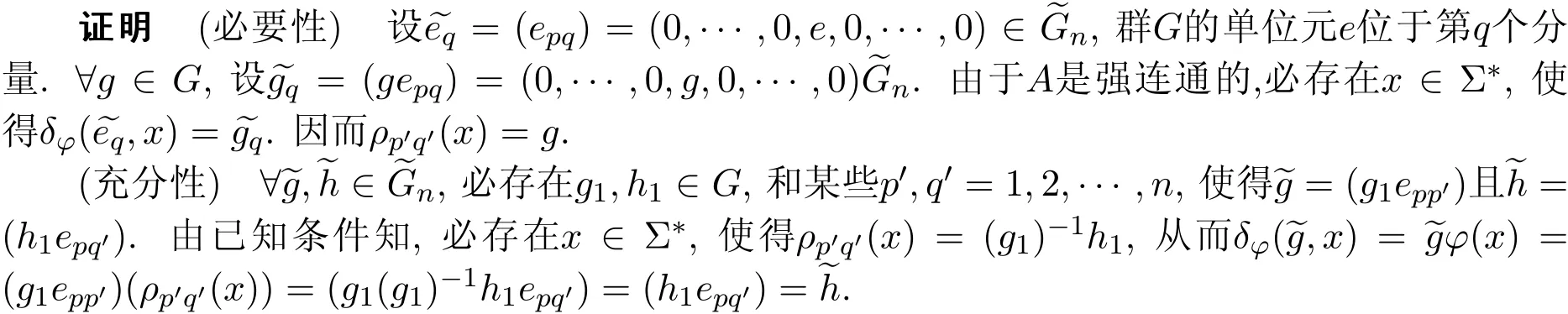
4 結論

自動機的強連通性是自動機理論中的一個重要研究內容.其良好的狀態轉移導致了研究工具的多樣化.在本文,將模糊自動機理論中的狀態集推廣到一般的代數群中.利用自動機的連通性和代數群理論,討論了群自動機的正則性.

[1]Hopcroft J E,Ullman J D.Introduction to Automata Theory,Languages and Computation[M].New York: Addison-Wesley,1979.

[2]Eilenberg S.Automata,Languages and Machines[M].Burlington:Academic Press,1976.

[3]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8:338-353.

[4]Wee W G.On generalizations of adaptive algorithm and application of the fuzzy sets concept to pattern classification[D].West Lafayette:Purdue University,June 1967.

[5]柏明強.模糊正則表達式與模糊有限態自動機的關系[J].純粹數學與應用數學,2000,16(4):1-6.

[6]Su Lan,Mo Zhiwen.Closure of the fuzzy finite state languages[J].Fuzzy Sets and Systems,1995,75:393-397.

[7]Lee E T,Zadeh L A.Note on fuzzy languages[J].Information Science,1969,1:421-434.

[8]Zoltan Esik,Guangwu Liu.Fuzzy tree automata[J].Fuzzy Sets and Systems,2007(1):1450-1460.

[9]柏明強.Fuzzy交換正則語言注記[J].四川師范大學學報:自然科學版,2005,28(4):391-393.

[10]Ito M.A representation of strongly connected automata and its applications[J].J.Comput System Sci., 1978,17:65-80.

[11]Sengupta A.On a group-matrix type automaton with output[J].Acta Math.Hung.1986,48(3-4):347-352.

[12]Barnes B I-I.Groups of automorphisms and sets of equivalence classes of input for automata[J].J.ACM, 1965,12:561-565.

[13]Feichtinger G.Some results on the relation between automata and their automorphism groups[J].Computing, 1966,1:327-340.

Connectedness of fuzzy automata and group automata

BAI Ming-qiang,MO Zhi-wen
(Colledge of Mathematics and Software Science,Sichuan Normal University,Chengdu610068,China)

In order to study the structure and properties of fuzzy automata,based on theory of general fuzzy finite state automata,a kind of fuzzy automata is introduced with its states set made up of algebra group matrix by algebra methods.The connectedness of fuzzy automata is discussed,then the regularity too.This is a foundation for further researches on fuzzy automata.

fuzzy automata,group,strongly connected

O235

A

1008-5513(2009)03-0454-05

2008-11-10.

國家自然科學基金(10671030),四川省青年科技基金項目(07ZQ026-114).

柏明強(1976-),講師,主要研究方向：形式語言與自動機.

2000MSC:03D12,68Q68