一種基于最小沖突集的約束沖突消解方法

劉曉平， 季 浩， 石 慧

（合肥工業大學計算機與信息學院VCC研究室，安徽 合肥 230009）

在協同設計中，不同設計者在網絡化平臺上依據各自經驗和理解對產品進行分工設計，實際過程中存在著大量相互影響、相互制約的約束關系。筆者所在的團隊在多年協同模板理論的研究過程中逐漸發現協同模板中約束關系的復雜 性[1]，當在協作過程中不同的設計選擇發生沖突時，如果設計者們對約束信息的組織關系把握不清楚，無疑會增加沖突消解的難度和設計過程的反復，降低協同設計的效率。

為了保證并行產品設計順利進行，文獻[2]采用改進的區間傳播算法用于實時在線檢測沖突，在約束網絡中沒有沖突時，給出傳播后變量的取值范圍。文獻[3]提出利用基于最小沖突集修補的算法，求解動態變化的約束滿足問題。但事實上都不能使設計者在變更約束的同時清楚了解約束條件之間的關系，而在約束信息發生沖突時，及時、準確地提取約束信息的制約關系、輔助設計者利用已有的知識進行協商調整約束信息是建立以人為中心的沖突消解方法的關鍵。

本文主要工作是從最小沖突集的角度出發，分析最小沖突集元素個數范圍和判定方法，并結合交邊算法[4]實現對最小沖突集的提取，通過算例說明最小沖突集，該方法對建立以人為中心進行控制和管理約束信息、消解約束沖突的有效性。

1 相關概念和性質

1.1 相關概念

一個工程設計問題實際上是多個約束條件滿足問題，即對滿足約束條件

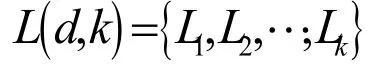
1.2 相關性質

為了方便描述和證明最小沖突集的相關性質，這里先給出交邊算法的數學描述和Helly 定理。

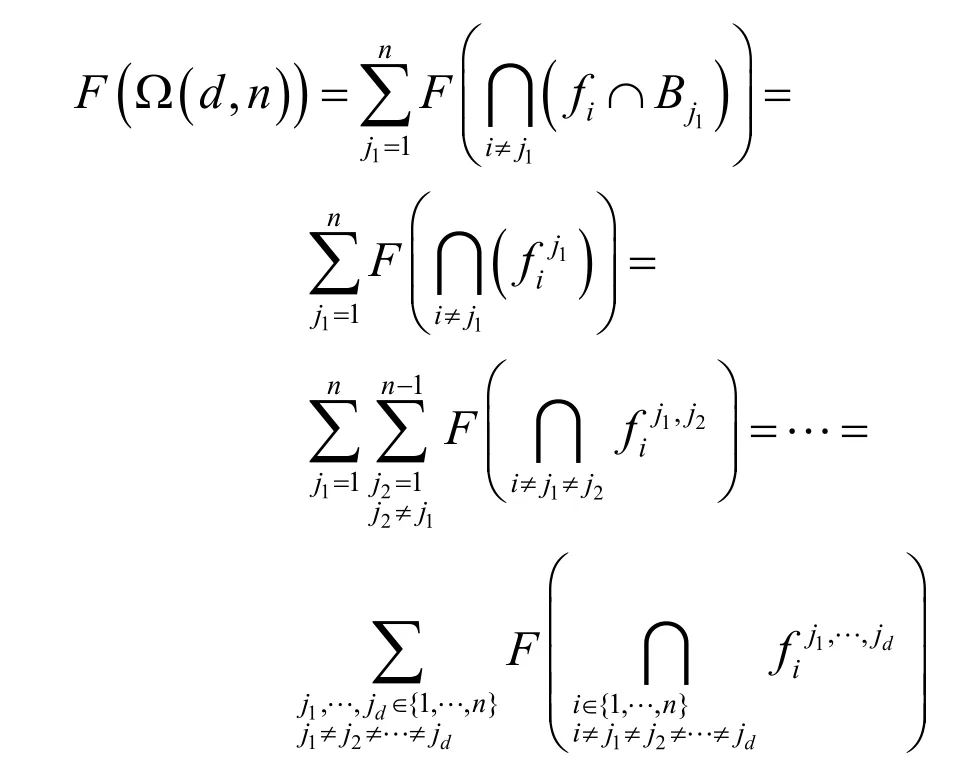
下面給出在交邊算法中提取最小沖突集時所用到的一些性質：

最小沖突集元素個數k 不小于2 是顯然。

若 1k d＞ + ，由最小沖突集的定義知

Ω ( d ,k)= ?， Ωi( d , k? 1)≠?， i = 1,… ,， k ? 1≥ d+1。

所以最小沖突集的元素個數k 滿足2 ≤ k ≤ d+1。

表1 約束冗余的判斷方法

對于 L1= L2的情況，通過指向 L1,L2所表示 區域的法向量是否相同來判斷冗余。

性質1 說明在d 維約束條件中，如果存在最小沖突集， 其元素個數k 的應該滿足 2 ≤ k ≤ d+1。性質2 指出判斷元素個數范圍為 [2, d+1]的沖突集方法，其證明由交邊算法的數學描述中易得。性質3 用來化簡冗余約束。在利用交邊算法判斷原約束集為沖突的同時，利用上述性質提取出最小沖突集和冗余約束。

2 約束沖突消解方法

本文在上述性質的基礎上，結合交邊算法提取最小沖突集和冗余約束，到達消解約束的目的。以下是約束沖突消解方法：

（1） 根據信息的屬性確定約束信息的維數d，由性質2 得最小沖突集的元素個數范圍。

（2） 將約束信息用改進的交邊算法，進行求解、檢測沖突和記錄相關信息。改進的交邊算法的非形式的描述如下：

Step 6 在記錄信息中依據上述的性質，化簡冗余約束信息，并提取 2k = 的最小沖突集。

Step 7 選取k s= 的最小沖突集，滿足：

Step 8 若 s ≤ d+1，則轉Step 7。否則算法結束。

（3） 由記錄的信息，去除冗余信息并提取最小沖突集。

（4） 對最小沖突集中的約束序號進行編碼，通過對編碼的運算，方便以后查找關鍵的約束信息。

（5） 設計者依照保留最多的約束、指定的約束等準則或要求，進行協商消解沖突。

3 算法示例

下面給出一個算例，假設設計者在進行約束沖突消解時，以保留最多約束條件為準則。

例：

由于線性約束是2 維的，只可能存在元素個數是2 或3 的最小沖突集。通過改進的交邊算法判定該約束集是沖突的，并得到如表2 的矛盾信息記錄。

表2 矛盾信息記錄

對最小沖突集中的約束進行01 編碼：

將編碼相加得：11010221，因有3 個最小沖突集，每個約束至多參與2 個最小沖突集，所以至少要剔除兩個約束，才能使得沖突消解。所以依據保留最多約束條件的準則，應當剔除約束條 件 L2, L3,L6。

圖1 約束條件的直觀圖

4 結 束 語

為了使設計者在協同設計中能清晰地把握約束信息的制約關系，有效地去除冗余信息、消解約束沖突。本文從最小沖突集的角度出發，在分析最小沖突集的相關性質和交邊算法的基礎上，提出了利用改進交邊算法提取最小沖突集，方便設計者按照一定的準則去除沖突約束信息。由于對最小沖突集剔除部分約束信息，需要建立在設計者的相關知識和準則上，并且在約束信息非常多的情況下，設計者不容易利用抽象思維完全把握約束信息之間的關系，而可視化具有細致、完善地展現約束信息，使設計者清晰、直觀地了解約束信息之間的關系，所以下一步工作將考慮結合約束信息可視化手段，研究可視約束信息、交互式處理沖突的方法。

[1] 劉曉平, 石 慧, 毛崢強. 協同模板中的信息可視化[J]. 計算機輔助設計與圖形學學報, 2005, 17(10)： 2334-2338.

[2] 朱湘毅, 唐 泉, 陳文培, 等. 并行工程中基于約束的沖突檢測研究[J]. 機械科學與技術, 2000, 19(5)： 849-852.

[3] 孫吉貴, 高 健, 張永剛. 一個基于最小沖突修補的動態約束滿足求解算法[J]. 計算機研究與發展, 2007, 44(12)： 2078-2084.

[4] 宋恩民, 黃文奇. 判斷具有多線性約束條件的凸空間是否為空的交邊算法[J]. 計算機學報, 1996, 19(9)： 704-708.

[5] Dimitri P Bertsekas, Angelia Nedic, Asuman E Ozdaglar. Convex analysis and optimization [M]. 北京： 清華大學出版社, 2006. 112-165.