會議籌備的優化模型

程 麗，胡英武，李代華，余素娟，吳丹萍

(金華職業技術學院師范學院，浙江金華 321017)

會議籌備的優化模型

程 麗，胡英武，李代華，余素娟，吳丹萍

(金華職業技術學院師范學院，浙江金華 321017)

利用數學規劃和概率統計知識對會議籌備問題進行了討論，從經濟、方便、代表滿意等方面出發，建立了預定賓館客房的0－1規劃以及相應的線性規劃。在一些合理的假設下，給出租借會議室、租用客車的方案，從而使租借會議室與租用客車的總費用盡可能少。最后，指出了模型中沒有考慮進去的因素，并提出了模型的改進方向，以滿足實際的要求。

會議籌備;0－1規劃;窮舉法

1 問題的提出

2009年，高教社杯全國大學生數學建模競賽D題提出會議籌備問題。某會議服務公司負責承辦一屆全國性會議，會議籌備組要為與會代表預訂賓館客房，租借會議室，并租用客車接送代表。由于預計會議規模龐大，而適于接待這次會議的幾家賓館的客房和會議室數量均有限，所以只能讓與會代表分散到若干家賓館住宿。為了便于管理，除了盡量滿足代表在價位等方面的需求之外，所選擇的賓館數量應該盡可能少，并且距離上比較靠近。再者，如果預訂客房的數量大于實際用房數量，籌備組需要支付一天的空房費，而若出現預訂客房數量不足，則將造成非常被動的局面，引起代表的不滿。會議期間，有一天的上下午各安排6個分組會議，籌備組需要在代表下榻的某幾個賓館租借會議室。租借客車方面:由于事先無法知道哪些代表準備參加哪個分組會，籌備組需向汽車租賃公司租用客車接送代表，現有45座、36座和33座3種類型的客車，租金分別是半天800元、700元和600元。本文通過數學建模的方法，從經濟、方便、代表滿意等方面，為會議籌備組制定一個預訂賓館客房、租借會議室、租用客車的合理方案。

2 問題的假設

1) 車輛都靠邊并沿直線行駛。

2) 6個 分組會議都同時召開，上午和下午安排的會議場地不變，參加的代表也不變。

3)上午6場會議的內容是相同的，下午6場會議的內容相同。

4) 當奇數個人去住雙人間時當偶數個人去處理。

5) 一輛客車可以送代表去不同的目的地。

6) 每輛客車盡可能載滿，一個賓館沒載滿可到其他賓館載滿。

7) 考慮時間問題，避免代表遲到，每輛客車每半天只送兩趟即客車在出發點只能出發兩次。

3 符號說明

Pi:表示以往幾屆已到人數占發來回執人數的百分比。(i=1，2，3，4)

P:表示以往幾屆已到人數占發來回執人數百分比的平均值。

dij:表示第i個賓館到第j個賓館的客車行駛距離。(i、j=1，2，…，10)

u:租用45座客車的數量。

v:租用36座客車的數量。

w:租用33座客車的數量。

4 問題的分析和模型的建立與求解

4.1 利用概率知識求出本屆會議可能參加代表的住房情況

根據D題附表3的以往幾屆會議代表回執和與會情況，求出以往幾屆會議已到人數占發來回執人數的百分比。

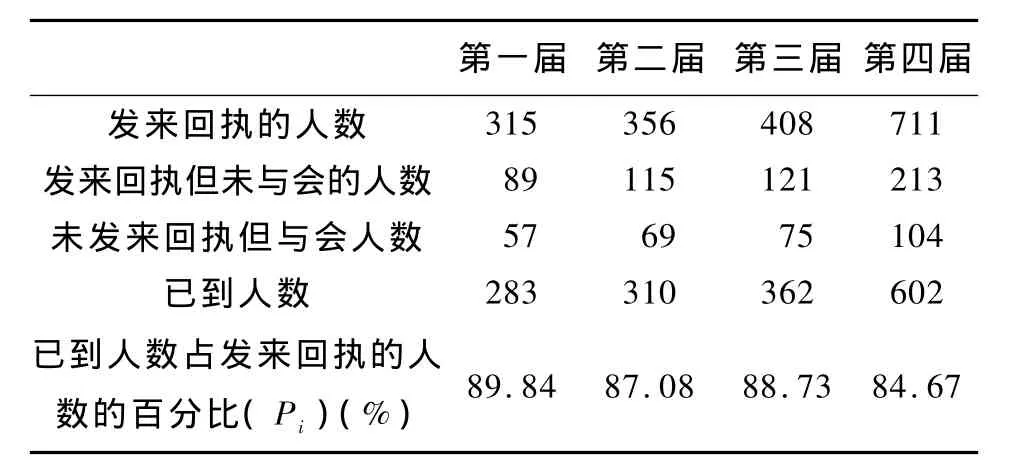
表1 以往幾屆已到人數占發來回執人數的百分比

87.58% 。從經濟角度出發，為了使預訂的客房不出現浪費或不足的局面，根據P值，對D題附表2的本屆會議的代表回執中有關住房要求的信息做一定的處理，讓它更符合實際。

表2 本屆會議可能參加的代表住房要求的情況 人

由表2求出本屆會議可能參加的人數為655人。再根據D題附表1的數據，對10個賓館各個價位的房間數量進行統計得表3。

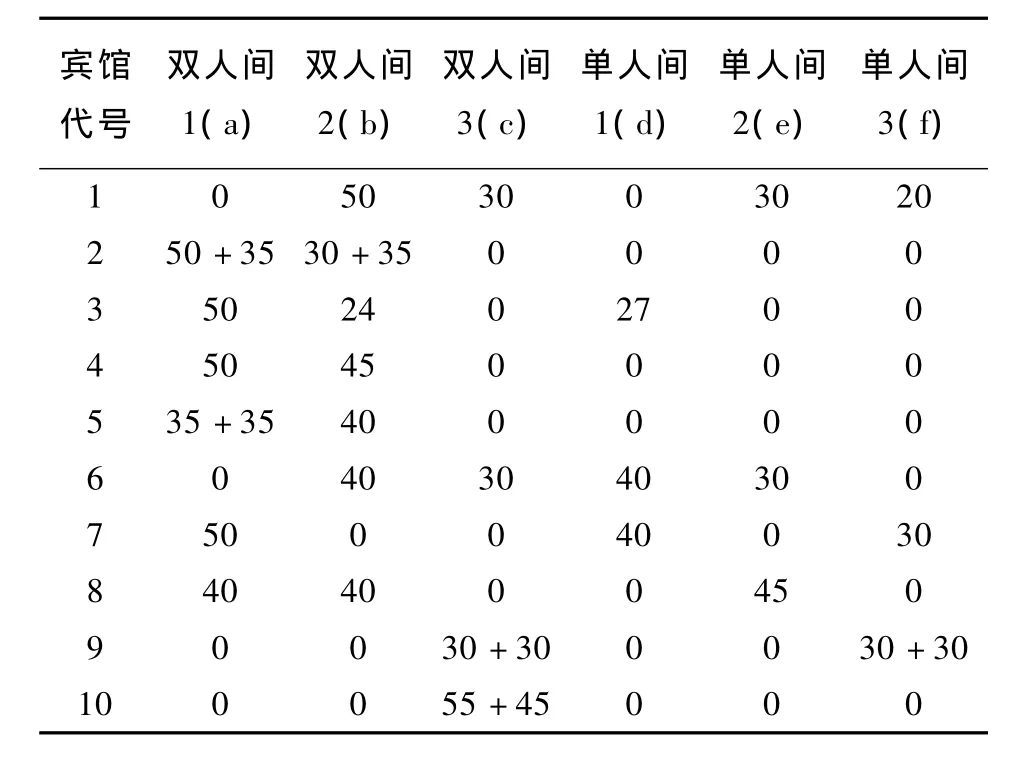
表3 10個賓館各個價位的房間數量 間

4.2 建立選擇賓館的模型

為了便于管理，首先要滿足所選的賓館數量盡可能少的要求，因此，對于賓館的房間，我們要充分地利用。在滿足合住的要求下，在安排獨住時，可以把獨住的人安排單人間或讓一個人單獨住一個雙人間。基于此原則，以賓館數量盡可能少為目標，建立如下的0－1規劃模型:xi=0或1(0表示不選擇第i個賓館，1表示選擇第i個賓館)。

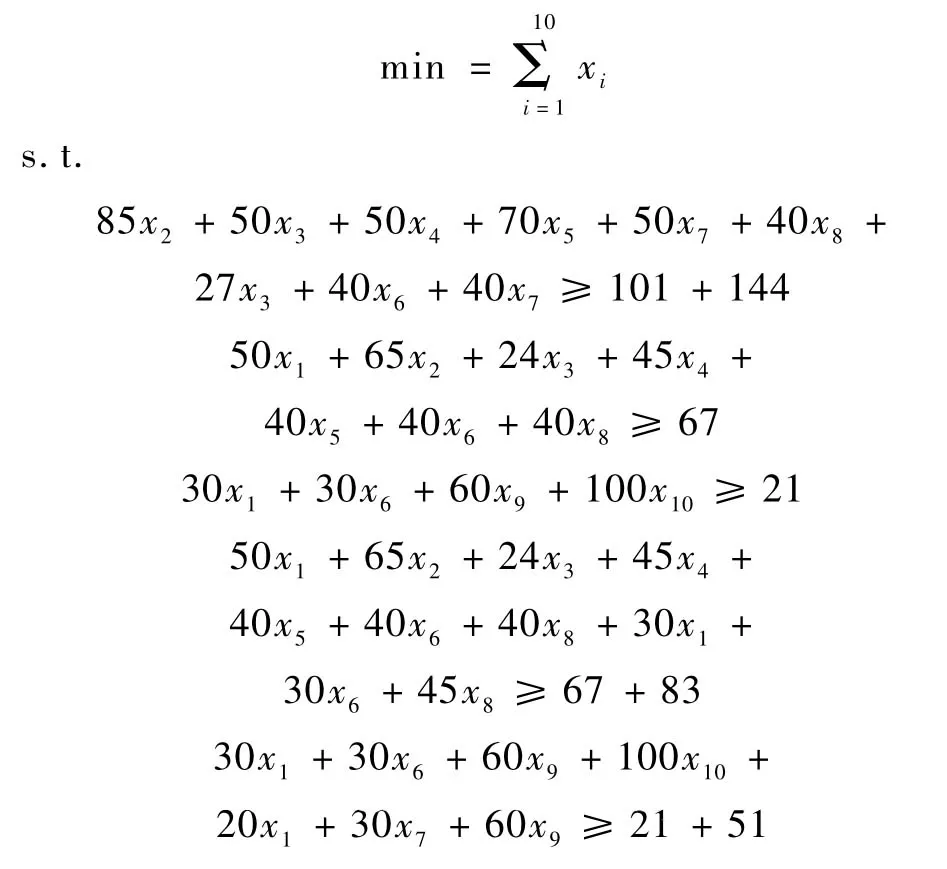
運用Lingo程序，求得有兩種解:第一種x1=x2=x3=x7=1，其他為0;第二種 x1=x2=x5=x7=1，其他為0。

當 x1=x2=x3=x7=1，其他為0 時，xi=4，d11=d22=d33=d77=0，d12=150m，d23=750 m，d27=450 m，d13=900 m，d37=1 200 m，d17=300 m，比較得出:max dij=d37=1200 m。

當x1=x2=x5=x7=1，其他為0時，xi=4，d11=d22=d55=d77=0，d12=150 m，d15=600 m，d17=300 m，d25=750 m，d27=450 m，d57=300 m，比較得出:max dij=d25=750 m。

通過兩種結果的比較，d37=1 200 m>750 m=d25，說明賓館 1、2、5、7 距離上比較靠近，因此選擇這4個賓館安排代表。

4.3 建立已選擇賓館的客房預定模型

從經濟、代表滿意等方面出發，以住房總價格盡可能少為目標，為會議籌備組制定一個向1、2、5、7這4家賓館預定客房的方案。設

x1b:表示賓館1價格為180元/天普通雙標間的預定間數。

x1c:表示賓館1價格為220元/天商務雙標間的預定間數。

x1e:表示賓館1價格為180元/天普通單人間的預定間數。

x1f:表示賓館1價格為220元/天商務單人間的預定間數。

x7a:表示賓館7價格為150元/天普通雙標間的預定間數。

x7d:表示賓館7價格為160元/天商務單人間的預定間數。

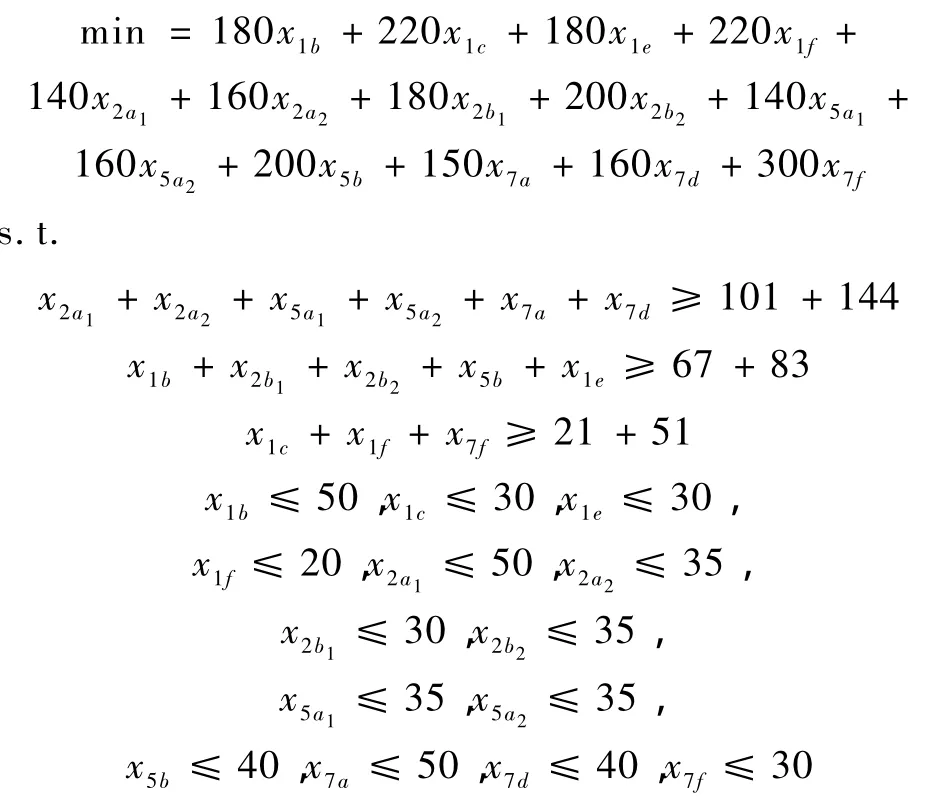
x7f:表示賓館7價格為300元/天商務套房(1床)的預定間數。x1b，x1c，x1e，x1f，x2a1，x2a2，x2b1，x2b2，x5a1，x5a2，x5b，x7a，x7d，x7f為非負整數。

利用lingo程序解得最優值為82 400元，這時，x1b=50、x1c=30、x1e=30、x1f=20、x2a1=50、x2a2=35、x2b1=30、x2b2=0、x5a1=35、x5a2=35、x5b=40、x7a=50、x7d=40、x7f=22。

由于獨住可安排單人間，或讓一人單獨住一個雙人間。因此，雙人間在先滿足合住的前提下，余下的安排獨住，具體分配見表4。

要求合住2的男代表出席人數為奇數，此多余的代表只能讓他單獨住雙人間，不妨把他安排在賓館1。從上表中可以求出，賓館1居住的人數為178人，賓館2居住的人數為174人，賓館5居住的人數為166人，賓館7居住的人數為137人。

4.4 制定租借會議室和租用客車的合理方案

會議期間，有一天的上下午各安排6個分組會議，由模型的假設，我們只考慮半天的安排。在預訂賓館的基礎上，對分組會議人數的確定按以下兩種情況進行討論。

1) 會議人數以會議室規模為準

相比之下，租用客車的半天租金比租借會議室的半天費用要高很多，因此不租車應是最優安排。我們在1、2、5、7每個賓館都租借會議室，在這個賓館住的就在這個賓館開會。設

表4預定的賓館客房分配情況

h11:表示賓館1價格為1 500元/半天會議室的租借間數。

h12:表示賓館1價格為1 200元/半天會議室的租借間數。

h13:表示賓館1價格為600元/半天會議室的租借間數。

h21:表示賓館2價格為1 000元/半天會議室的租借間數。

h22:表示賓館2價格為1 500元/半天會議室的租借間數。

h23:表示賓館2價格為300元/半天并容納45人的會議室的租借間數。

h24:表示賓館2價格為300元/半天并容納30人的會議室租借的間數。

h51:表示賓館5價格為1 000元/半天會議室的租借間數。

h52:表示賓館5價格為1 500元/半天會議室的租借間數。

h53:表示賓館5價格為500元/半天會議室的租借間數。

h71:表示賓館7價格為800元/半天會議室的租借間數。

h72:表示賓館7價格為300元/半天會議室的租借間數。

h73:表示賓館7價格為1 000元/半天會議室的租借間數。

以租借會議室半天的總費用最少為目標，可得整數規劃:

h11，h12，h13，h21，h22，h23，h24，h51，h52，h53，h71，h72，h73為非負整數。

解得 h11=h21=h23=h51=h53=h71=1，其余為0，即在賓館1租借一個價格1 500元/半天的會議室，在賓館2租借一個價格1 000元/半天的會議室、一個價格300元/半天并容納45人的會議室，在賓館5租借一個價格1 000元/半天的會議室和一個價格500元/半天的會議室，在賓館7租借一個價格800元/半天的會議室，此時不需要租車。半天租借會議室的總費用為5 100元，一天為10 200元。

2)會議人數平均分配

根據本屆會議可能參加的人數為655人，計算出每個分組會議的人數大約為 109人，即每個會議室的規模應大于109人。若還是在1、2、5、7每個賓館都租借會議室，則必定有一個賓館將租借2個會議室，這樣到此賓館開會的大約有220人，而這4個賓館居住的人數都不超過180人，因此籌備組必須要租用客車接送代表。

雖然租用客車的租金是以半天計算，但是考慮時間問題，為了避免代表遲到，假設每輛客車每半天只送兩趟，并盡量讓客車坐滿，一個賓館沒載滿可到其他賓館載滿，一趟可以送代表去不同的目的地。

如果6個會議室分別租借在4個賓館，則有2個賓館要租2個會議室或有1個賓館要租3個會議室，用排列組合算出共有10種情況。

以賓館1、2各租兩個會議室，賓館5、7各租一個會議室為例，建立模型:

h73≤1，h11，h12，h21，h22，h51，h52，h71，h73為非負整數。

得 h12=h21=2，h51=h71=1，其余為 0，目標函數最優解為6 200元。但在賓館5租借了一個會議室，須把166－109=57人送到賓館1或2參加會議，同樣也須把賓館7的137－109=28人送到賓館1或2參加會議，于是又建立如下模型:

h11，h12，h21，h22，h51，h52，h71，h73為非負整數。

得 h12=h21=2，h51=h71=1，u=1，其余為 0，目標函數最優解為7 000元。

其余9種情況同樣建立規劃可得，其計算結果見表5。

如果6個會議室租借在3個賓館，則有4種情況，對于每一種情況，先不考慮要送的代表人數，求出租用會議室的最少費用，然后再考慮至少要送的代表，求出租借會議室和租用客車至少所需的總費用，見表6。

如果6個會議室租借在兩個賓館，則至少有137+166=303位代表要送，租用客車至少需u=2輛，w=2輛，即需租金2 800元，而不考慮任何限制，租6個規模大于109人會議室最優地點是h21=h51=h71=2，租金為5 600元，這樣半天總費用至少要8 400元。

如果6個會議室都租借在同一個賓館里，這是不能安排的。

綜上所述，要使總費用最少，應在賓館1中租借兩個價格為1 200元/半天的會議室，在賓館2租借兩個價格為1 000元/半天的會議室，在賓館5租借一個價格為1 000元/半天的會議室，在賓館7租借一個價格為800元/半天的會議室，并租用45座類型的客車一輛;或在賓館1租借選擇一個價格為1 200元/半天的會議室，在賓館2租借兩個價格為1 000元/半天的會議室，在賓館5租借一個價格為1 000元/半天的會議室，在賓館7租借兩個價格為800元/半天的會議室，并租用33座類型的客車兩輛，此時半天總費用都為7 000元，一天就為14 000元。

5 模型分析與改進

論文就會議籌備優化模型進行分析討論。在盡可能提高與會代表對住房滿意度的前提下來討論預定賓館客房的方案，計算出居住在賓館1、2、5、7各自的總人數;對于分組會議人數的不同情形，利用窮舉法列舉出各種會議室分布情況，進而求出租借會議室和客車的最省總費用。

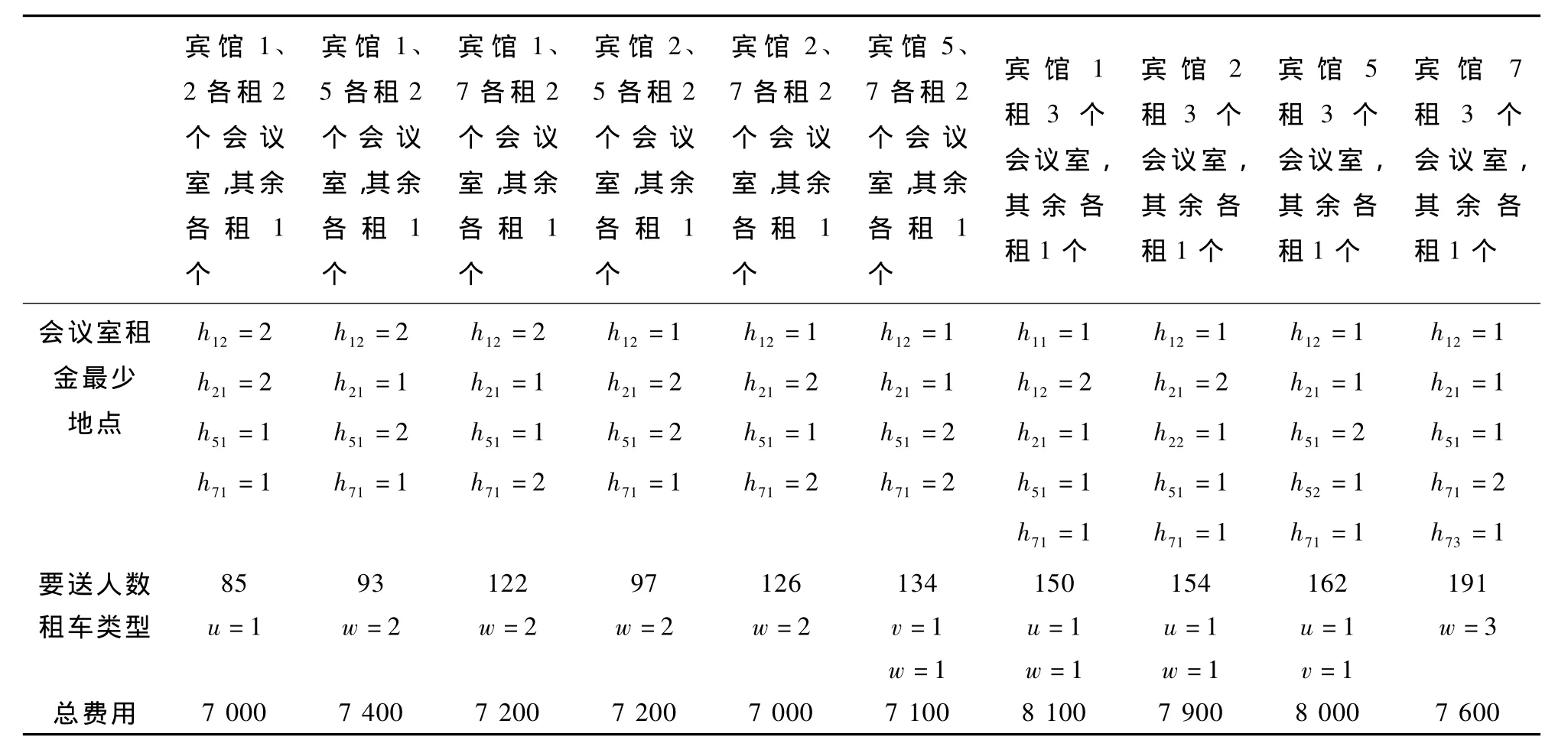
表5 在4個賓館都租借會議室以及客車租用的情況

表6 在3個賓館租借會議室以及客車租用的情況

在選擇會議室的時候，我們的模型還存在一些不足之處，即本文假設6個分組會議的內容是相同的，沒有考慮6個分組會議的內容互不相同，代表需到指定的會議室這一變因;在安排客車接送代表時，也只考慮每輛客車每半天只送兩趟，沒有考慮客車接送次數變化，而這些因素很可能會對模型的穩定性產生影響，不利于模型的推廣，模型有待于進一步地改進與優化。但無論如何，我們所建的模型對籌劃組的工作人員還是有一定的實際指導意義的。

［1］ 姜啟源.數學模型［M］.北京:高等教育出版社，2003.

［2］ 袁新生.Lingo和Excel在數學建模中的應用［M］.北京:科學出版社，2007.

［3］ 葉其孝.大學生數學建模競賽輔導材料(三)［M］.長沙:湖南教育出版社，1999.

［4］ 袁蔭棠.概率論與數理統計［M］.北京:中國人民大學出版社，2000.

［5］ 吳建國.數學建模案例精編［M］.北京:中國水利水電出版社，2005.

An Optimality Model of Conference Preparations

CHENG Li，HU Ying-wu，LI Dai-hua，YV Su-juan，WU Dan-ping

(Normal school of Jinhua College of Profession and Technology，Jinhua Zhejiang 321017，China)

An optimality model of conference preparations was discussed on the theory of mathematical programming and probability.First，some mathematical programming problems about hotels chosen and guestroom reservation were given from the perspectives of economy，convenience，and satisfaction of participants.Second，a reasonable plan for the Local Organizing Committee in their meeting room lease and coach lease by use of mathematical modeling is made under some reasonable hypothesis.Some fault and improvement about the model are pointed out in the end.

conference preparations;0－1 programming problem;exhaustive method

O 141.4

A

1005-0310(2010)01-0067-06

2009－10－08

程麗(1972—)女，浙江永康人，金華職業技術學院副教授，碩士，研究方向為最優化理論。

(責任編輯 李亞青)