帶有典型缺陷的金屬蜂窩夾層結構的共面力學性能研究①

孔祥皓,赫曉東

(哈爾濱工業大學復合材料與結構研究所,哈爾濱 150001)

0 引言

薄壁高溫合金蜂窩夾層結構因其既能滿足高超聲速飛行器對熱防護系統質量與體積的要求,又能解決防熱、隔熱、承載一體化設計難題而被越來越廣泛地應用于航空航天領域[1-3]。該結構屬于格柵夾層結構中的一種,中間層則為輕質多孔材料中的蜂窩材料。Gibson和Ashby利用材料力學中梁的彎曲變形理論建立了蜂窩芯子面內等效剛度理論模型[4]。Masters和Evans建立了蜂窩芯子面內等效模量的3種預報模型:彎曲模型、伸縮模型和鉸鏈模型[5]。Simone和Gibson利用數值模擬的方法研究了厚度分布不均勻對面內等效剛度的影響規律[6]。富明慧等人通過考慮蜂窩芯子壁的彎曲變形和伸縮變形克服了Gibson預報公式面內等效泊松比的不合理性[7]。Becker采用有限元法研究了蜂窩芯子高度對面內等效剛度的影響[8]。Silva和Gibson研究發現了蜂窩材料的彈性模量受蜂窩壁缺失的影響[9]。何景軒等對復合材料格柵結構的力學性能進行分析討論[10-14]。盧天健等探討了格柵結構的多功能應用設計[15-17]。范華林等在前人的理論基礎之上對格柵夾層結構的研究進展進行了較為全面而深入的總結[18-19]。可由于結構在制備或服役過程中可能產生缺陷,其力學性能受缺陷類型、尺寸和位置等諸多因素的影響,因此仍需進行大量的實驗來研究這類結構的變形及破壞規律。

本文對薄壁高溫合金蜂窩夾層結構在實際服役過程中可能產生的缺陷進行分類,并通過其共面拉伸與壓縮的宏觀力學性能實驗得到了結構的重要力學性能參數,研究了3種典型缺陷對結構共面力學性能的影響。對破壞后的試件的形狀變化及斷口形貌進行觀察,進而初步分析了結構在共面拉、壓載荷下的破壞機理。在高溫釬焊過程中鎳基高溫合金與釬料相互作用而導致材料強度、彈性模量等均發生改變,因此進行模擬計算時材料的基本參數均需要重新測量定義。本文所獲結論為結構設計及損傷容限體系的建立提供了必要的實驗基礎。

1 實驗

1.1 試件制備

文中的金屬面板和蜂窩芯子材料均選用鎳基高溫合金Haynes 214,其化學成分見表1。制備過程如下:首先將Haynes214薄壁材料用齒輪碾壓形成波紋板;再將波紋板進行激光點焊制成薄壁蜂窩芯子材料,最后通過高溫釬焊將金屬面板與蜂窩芯子焊接而成所需金屬蜂窩夾層結構。

表1 Haynes 214的化學成分Tab le 1 Com position of Haynes 214 %

薄壁格柵夾層結構的共面拉伸實驗是其力學性能測試中的一個難點,原因是結構的抗壓強度明顯小于抗拉強度以致實驗的夾持難度很難克服。需要在結構的焊接成型過程中,在蜂窩芯子材料的兩端添加等厚度的實體材料用以增加結構端部的抗壓強度,解決了共面拉伸實驗的夾持問題。根據蜂窩夾層結構的力學性能測試國標,要求試件的長度和寬度范圍內都至少包含4個以上完整的蜂窩單胞。本文所用的正六邊形蜂窩材料的單胞邊長和高度均為4mm,所以試件的長度和寬度都需要大于40mm。共面拉伸實驗樣件的標距取為70mm,寬度和厚度分別為40、4.5 mm。由于兩端各有10mm的實體加強段,所以試件的實際長度為90mm。共面壓縮實驗樣件的標距取為40 mm,寬度和厚度也分別為40、4.5 mm,拉伸和壓縮試件采用金屬材料加工中常見的線切割法進行制備。

1.2 缺陷分類

薄壁高溫合金蜂窩夾層結構是通過機械連接方式與機體裝配的,所以不可避免地需要在結構上制造宏觀缺陷。同時高超聲速飛行器的使用環境非常惡劣,其中的高速沖擊、周期性疲勞載荷及熱載荷也會使結構產生斷裂乃至擊穿破壞。根據實際情況可將這些缺陷分為以下3種典型缺陷類型:

(1)細裂紋(crack)缺陷:裂紋寬度遠小于晶胞尺寸,且裂紋長度與晶胞尺寸相當的對稱細長型缺陷類型。

(2)孔洞(hole)缺陷:破壞形狀為圓孔形,且半徑尺寸與晶胞尺寸相當的、多由沖擊載荷形成的缺陷類型。

(3)孔狀裂紋(notch)缺陷:裂紋寬度尺寸和裂紋長度尺寸均與晶胞尺寸相當的、對稱的半圓形缺陷類型。

拉伸試件的缺陷形狀及尺寸如圖1所示,3種缺陷均位于試件長度方向的中位線處,其中細裂紋長度、孔洞半徑和孔狀裂紋半徑均為5mm,均采用機械加工手段來制造缺陷。

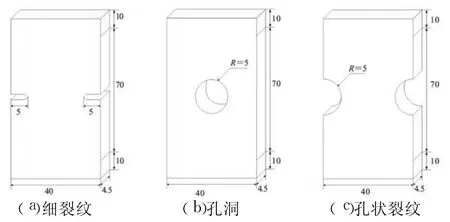
圖1 帶有細裂紋、孔洞、孔狀裂紋缺陷的拉伸試件的尺寸Fig.1 Size of tensile sample with crack hole and notch defects

1.3 力學性能測試

特別需要指出的是,通過實驗注意到鎳基高溫合金因在高溫釬焊過程中與釬料相互作用致使組織發生變化,于是其強度、彈性模量及塑性變形能力也隨之改變,因此在進行有限元模擬計算時,材料的基本參數均需重新測量定義。在圖2中,對比了Haynes214材料和釬焊后金屬蜂窩夾層結構的面板材料的拉伸力學性能,可清楚地觀察到材料的彈性模量和拉伸強度變化較小,基本可忽略,但其塑性變形能力大幅降低以致面板材料的彈塑性特征值必須重新定義,這也是后文中結構在共面拉伸實驗時應變較小及彈塑性過渡不明顯的主要原因。

本實驗的應力值是用載荷除以截面面積計算而得的,由于薄壁蜂窩夾層結構的中間層為周期性多孔材料,以致所得應力值較小,且不能反映金屬材料中的實際應力。結構的抗拉強度和抗壓強度值雖然偏低,但由于其密度很小,所以比強度乃至比剛度卻非常出眾。

圖2 金屬蜂窩夾層結構的面板的拉伸應力-應變曲線Fig.2 Tension stress-strain curves o f facep late ofm etalhoneycomb sandwich

金屬蜂窩夾層結構的共面拉伸強度在65～70 MPa之間,如圖3(a)所示。因為缺陷的尺寸約占結構橫截面尺寸的25%,所以帶有3種典型缺陷結構的理論抗拉強度應該衰減為原強度值的75%,即50MPa以上。這里只有帶有Hole缺陷的結構的共面拉伸強度能夠達到這個數值范圍,如圖3(c)所示;而帶有Crack缺陷和Notch缺陷的結構的共面拉伸強度均低于此強度值,如圖3(b)、(d)所示。而且注意到無缺陷和帶有Hole缺陷的結構的拉伸應力-應變曲線經歷了較長的塑性屈服階段,因此其應變也比較大,并且它們都是在達到強度極限時突然斷裂失效。反觀帶有Crack缺陷和Notch缺陷的結構的拉伸應力-應變曲線基本還處于線彈性階段或剛剛過度至塑性階段,斷裂失效時應變也較小,并且在發生斷裂后均具有一定的殘余強度。

金屬蜂窩夾層結構的共面壓縮強度在75～80 MPa之間,如圖4(a)所示。由于試件的長厚比較大,且結構中間層為薄壁多孔材料,導致其共面壓縮破壞模式常出現結構局部失穩;由于薄壁蜂窩夾層結構的有效橫截面面積較小,導致試件兩端因局部應力過大而發生塑性屈曲變形。這2種薄壁格柵夾層結構所特有的非常規破壞形式致使測試所得共面壓縮強度值并不能真實反映結構的抗壓性能。但可以確定,當壓縮強度接近80 MPa時,結構即使不發生局部失穩也會因端部的塑性屈曲而失效破壞。

在共面壓縮加載過程中,結構會發生不同程度的屈曲變形,所以在壓縮實驗中結構的應變數值遠大于拉伸實驗,但這里的應變所指的并不單單是實際意義上的材料應變,而是材料應變與結構應變的疊加。

圖3 金屬蜂窩夾層結構共面拉伸應力-應變曲線Fig.3 Tension stress-strain curves a long XY of metal honeycomb sandwich

帶有Crack缺陷的蜂窩夾層結構在共面壓縮性能測試中也可達到極限抗壓強度80 MPa附近,但也有在低強度值時發生破壞的情況存在,如圖4(b)所示。抗壓強度值不穩定的現象在帶有Hole和Notch缺陷的蜂窩夾層結構壓縮性能測試中也同樣存在,不同的是在后2種情況下強度值都達不到極限抗壓強度80 MPa,如圖4(c)、(d)所示。

圖4 金屬蜂窩夾層結構共面壓縮應力-應變曲線Fig.4 Com pression stress-strain curves along XY direction of metal honeycomb sandwich

2 結果與分析

2.1 缺陷對力學性能的影響

在共面拉伸力學性能測試中,通過對比無缺陷試件與帶有3種典型缺陷試件的實驗結果,可清楚地觀察到Crack和Notch缺陷對金屬蜂窩夾層結構拉伸強度的衰減影響最大。其中帶有Notch缺陷的試件的抗拉強度值較為穩定,而帶有Crack缺陷的試件的抗拉強度值上下波動較大。帶有Hole缺陷的試件的抗拉強度基本上等于具有等效面積的無缺陷試件的抗拉強度,所以Hole缺陷對結構的抗拉性能影響最小,僅為缺陷自身所造成的結構在尺寸上的縮減。

在共面壓縮力學性能測試中也是通過對比4組實驗結果,注意到除了帶有Crack缺陷的少數試件可達到無缺陷試件的抗壓強度外,基本上每種缺陷都會使結構強度產生或多或少地衰減,而且3種典型缺陷都會使結構的抗壓強度產生一定的波動幅度,在3組實驗中都存在一些試件的抗壓強度較接近無缺陷情況。其中帶有Hole缺陷的試件的抗壓性能并沒有像其在抗拉性能中表現出來的優勢,反而強度衰減較為明顯。

2.2 結構在共面拉伸載荷下的破壞機理

在共面拉伸實驗中發現結構的破壞形式為斷裂破壞,且可通過強度衰減的計算結果來輔助判斷帶有典型缺陷結構的破壞機理,每種缺陷下結構具體的破壞機理也不盡相同。在無缺陷與帶有Hole缺陷試件的拉伸曲線中可看到比較明顯的塑性階段,表明在這2種情況下結構是先后經歷彈性變形和塑性屈服并達到強度值后發生斷裂破壞的,與金屬材料的拉伸曲線比較接近。所以,帶有Hole缺陷結構的共面拉伸破壞機理與無缺陷結構相同,均為材料達到自身屈服極限后的失效斷裂。而在帶有Crack和Notch缺陷試件的拉伸曲線中塑性屈服段或是極短或是根本不存在,說明在這2種情況下結構是在經歷彈性階段后直接發生脆性斷裂的,其拉伸應力-應變曲線也與脆性材料相似。通過觀察實驗曲線和實驗樣件的斷口形貌,可判斷結構是由于在2種裂紋尖端的應力集中引發裂紋擴展而最終導致斷裂的,帶有3種典型缺陷的試件在共面拉伸測試后的斷裂形貌如圖5所示。實驗曲線中所見的殘余強度反映了結構在裂紋擴展且未完全斷裂階段的強度。

圖6為蜂窩夾層結構的拉伸斷裂剖面的金相圖。由圖6可知,區域Ⅰ為結構面板材料基體,區域Ⅱ為蜂窩芯子材料基體,區域Ⅲ為釬焊合金區。靠近基體的深灰色相是因釬焊合金區所含化合物相中的易于擴散的元素向母材中擴散而形成的連續固溶體組織;在釬焊合金區中彌散分布于鎳基固溶體當中的不連續的黑灰色相為共晶體組織;而在面板與蜂窩芯子材料中均存在從釬焊連接邊緣至基體中梯度分布的白色細小顆粒相,而且其在晶界處呈現出明顯的聚集現象,經過證明這是由于蜂窩夾層結構中的釬焊合金區所含B元素向面板以及蜂窩芯子材料的基體中進行擴散所導致的,并且因為蜂窩芯子材料的厚度僅為76μm且在焊接過程中雙面接觸釬料以至于在蜂窩芯子基體中白色顆粒相近似于均勻分布,可在厚度達200μm且在焊接過程中單側接觸釬料的面板材料基體中卻能清楚地看到明顯的擴散梯度。也正是由于材料在高溫釬焊過程中所發生的組織演變導致了整體結構的拉伸力學性能隨之發生改變,進而使得焊接成型的高溫合金蜂窩夾層結構在側拉實驗中的破壞模式和斷口形貌近似于脆性材料的拉伸斷裂。

圖5 金屬蜂窩夾層結構的拉伸斷裂失效Fig.5 Tensile fracture failure of metal honeycomb sandw ich

圖6 蜂窩夾層結構剖面的微觀照片Fig.6 Cross-section micrograph of super alloy honeycom bsandwich

為進一步證明實驗結果的準確性,利用ABAQUS有限元軟件對帶有以上典型缺陷的結構進行拉伸模擬。在計算過程中利用顯性分析,嵌入損傷模型,得到了這幾種結構的拉伸破壞形貌(如圖7),其模擬結果與實驗試件斷裂形貌基本吻合。

2.3 結構在共面壓縮載荷下的破壞機理

在共面壓縮實驗中,結構的破壞形式主要為局部失穩和屈曲變形,且由于極限抗壓強度的存在,并不能通過強度衰減的計算結果來判斷結構實際的破壞機理。與拉伸實驗不同的是3種缺陷下結構的破壞機理基本相同,而且在每種缺陷試件的失效破壞中都包含局部失穩和屈曲變形2種破壞形式,這也是試件強度波動較大的最主要原因。在無缺陷試件的共面壓縮實驗中就可看出,由于結構中間部位應力分布均勻,端部受壓而應力集中所致端部屈曲變形,這也是造成共面壓縮試件存在極限抗壓強度的主要原因。圖4(a)中無缺陷試件2的共面壓縮實驗曲線較為特殊,在結構的應變達到1%附近時應力值出現短暫的下降趨勢,而后又繼續上升至壓縮破壞強度后再次衰減。這是由于在壓縮加載過程中結構內部連接失效所引起的結構屈曲變形造成的,而且結構在屈曲變形過程中并未發生失穩現象。結構的內部連接失效會因遇到焊接加強點而終止破壞,此后也就是圖中屈曲變形停止而強度繼續攀升的曲線二次上升段。應力二次上升階段的曲線斜率基本相同,即結構的彈性模量保持不變,這也證明了之前發生的結構屈曲變形并非結構的整體失效破壞,而僅僅是局部的連接失效,其仍然保持原有的強度與彈性模量。

圖7 含有典型缺陷結構的拉伸斷裂模擬結果Fig.7 Simulation results of tensile failure for the structure with typical defects

帶有Crack、Hole和Notch缺陷的試件在共面壓縮實驗中的破壞機理主要可以分為以下2種:

(1)結構屈曲失效,這類失效形式是指在結構內部應力較大時特別是當達到極限抗壓強度時,于端部或缺陷附近區域發生的對稱性結構屈曲變形。通過圖8(a)可直觀地觀察到,上2種情況即為因端部發生塑性屈曲變形失效試件的俯視圖與正視圖,而后2種情況則是因缺陷部位附近區域的屈曲變形導致破壞的試件的俯視圖與側視圖。

(2)局部失穩失效,這類失效形式伴隨著結構在缺陷處的彎曲或錯位,而且往往導致結構的整體抗壓強度偏低。通過圖8(b)的俯視圖,可清楚地觀測到4個試件都在中間部位附近區域發生與上圖相似的寬度方向上的貫穿性面板屈曲變形;但由圖8(b)的側視圖可見,與第一種情況不同的是這里的面板屈曲是非對稱性的,而且導致了結構的失穩變形。

若想克服結構在共面壓縮測試中所產生的局部失穩現象,則需要減小試件的標距;若想克服端部塑性屈曲變形,則需要增加試件端部的橫截面積。前者會使試件的尺寸規格不符合國標要求,后者因改變結構的真實尺寸而減弱實驗結果的實際意義。這2種破壞模式既是不可消除的又是飛行器在服役過程中真實存在的。

圖8 蜂窩夾層結構在共面壓縮實驗中的破壞模式Fig.8 Failure model of metal honeycomb sandwich structure in compression test

3 結論

(1)在高溫釬焊過程中鎳基高溫合金與釬料相互作用導致其塑性變形能力大幅降低,這也是在共面拉伸實驗中金屬蜂窩夾層結構的應變較小以及彈塑性過度不明顯的主要原因。因此在進行模擬計算時,結構面板材料的彈塑性特征值必須重新定義。

(2)在共面拉伸載荷狀態下,Hole缺陷并不破壞金屬材料所特有的彈塑性,并且其破壞模式與無缺陷結構相似;而其他2種缺陷卻會導致結構直接發生脆斷,破壞機理為裂紋尖端應力集中導致裂紋擴展而失效斷裂。

(3)在共面壓縮載荷狀態下,結構的失效模式相近,主要分為結構屈曲和局部失穩,且失效部位多發生在缺陷所在水平區域。其中結構屈曲為理想破壞模式,而局部失穩常導致結構整體抗壓強度偏低。

[1] Tirpak J,John A.The flight to orbit[J].Air Force Magazine,1998,81(1):41-44.

[2] Correll B,John T.Destiny in space[J].Air Force Magazine,1998,81(2):11-16.

[3] Correll B,John T.The integration of aerospace[J].Air Force Magazine,1999,82(2):10-16.

[4] Gibson L J,Ashby M F.Cellular solids:structure and properties,second edition[M].Cambridge:Cambridge University Press,1997.

[5] Masters IG,Evans K E.Models for the elastic deformation of honeycombs[J].Composite Structures,1996,35:403-422.

[6] Simone A E,Gibson L J.Effects of solid distribution on the stiffness and strength ofmetallic foams[J].Acta Materialia,1998,46(6):2139-2150.

[7] 富明慧,尹久仁.蜂窩芯層的等效彈性參數[J].力學學報,1999,31(1):113-118.

[8] Becker W.Closed form analysis of the thickness effect of regular honeycomb core material[J].Composite Structures,2000,48:67-70.

[9] Silva M J,Gibson L J.The effects of non Cross-section periodic micro structure and defects on the compressive strength of two Cross-section dimensional cellular solids[J].International Journal of Mechanical Science,1997,39(5):549-563.

[10] 何景軒,何國強,任明法.復合材料格柵結構屈曲特性分析[J].固體火箭技術,2008,31(4):389-392.

[11] 何景軒,何國強,任明法,等.復合材料格柵結構穩定性分析[J].固體火箭技術,2009,32(3):331-335.

[12] 章繼峰,張博明,杜善義.平板型復合材料格柵結構的增強改進與參數設計.[J].復合材料學報,2006,23(3):153-157.

[13] Li G Q,Cheng JQ.A generalized analytical modeling of grid stiffened composite structures[J].Journal of Composite Materials,2007,41(24):2939-2969.

[14] Fan H L,Meng F,Yang W.Sandwich panels with Kagome lattice cores reinforced by carbon fibers[J].Composite Structures,2007,81(4):533-539.

[15] 盧天健,劉濤,鄧子辰.多孔金屬材料多功能化設計的若干進展[J].力學與實踐,2008,30(1):1-9.

[16] 蔣詩才,邢麗英,李斌太,等.格柵結構吸波性能探索研究[J].航空材料學報,2006,26(3):196-198.

[17] Fan H L,Yang W,Chao Z M.Microwave absorbing composite lattice grids[J].Composite Science and Technology,2007,67:3472-3479.

[18] 范華林,楊衛.輕質高強點陣材料及其力學性能研究進展[J].力學進展,2007,37(1):99-112.

[19] 范華林,金豐年,方岱寧.格柵結構力學性能研究進展[J].力學進展,2008,38(1):35-52.