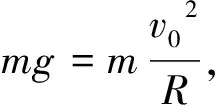豎直平面內圓周運動中的拋體運動
馮明志
(徐州一中 江蘇 徐州 221002)
圓周運動問題是力學中的基本問題之一,中學主要研究在水平面內和豎直面內的兩種圓周運動.通常我們認為,只要物體運動時有提供與運動方向相垂直的向心力,物體就能在一定軌道上做圓周運動,而事實上由于物體所處的運動狀態和受力特征不同,不是每種圓周運動都能發生;在一定情況下,就會由圓周運動變拋體運動.這類問題總是出現在變速圓周運動中,而豎直平面內的圓周運動是典型的變速圓周運動,下面我們主要通過豎直平面的圓周運動來探討這一問題.
1 圓軌道內側的拋體運動
當物體沿圓軌道內側做圓周運動時(如過山車),如果軌道對物體有作用力,只能是垂直支承面向內的壓力;當軌道與物體間沒有作用力時,物體將做拋體運動.
【例1】一質量m=2 kg的小球從光滑斜面上高h=3.5 m處由靜止滑下,斜面底端緊接著一個半徑R=1 m的光滑圓環[圖1(a)],求:
(1)小球滑至圓環頂點時對環的壓力;
(2)小球至少應從多高處靜止滑下才能越過圓環最高點;
(3)小球從h′=2 m處靜止滑下時將在何處脫離圓環.(取g=10 m/s2)
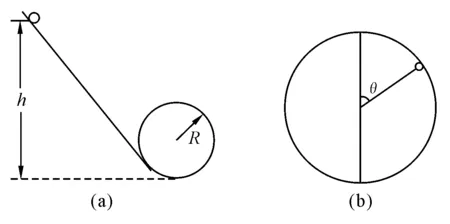
圖1
解:(1)設小球滑至環頂時速度為v,所受環的壓力為N,由機械能守恒和圓周運動條件得(以軌道最低點為零勢面)
(1)
(2)
聯立解得
N=40 N
(2)剛好越過圓環時,在環頂由重力提供向心力,球與環間的壓力等于零,在(1)解法中令N=0,可得
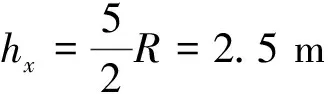
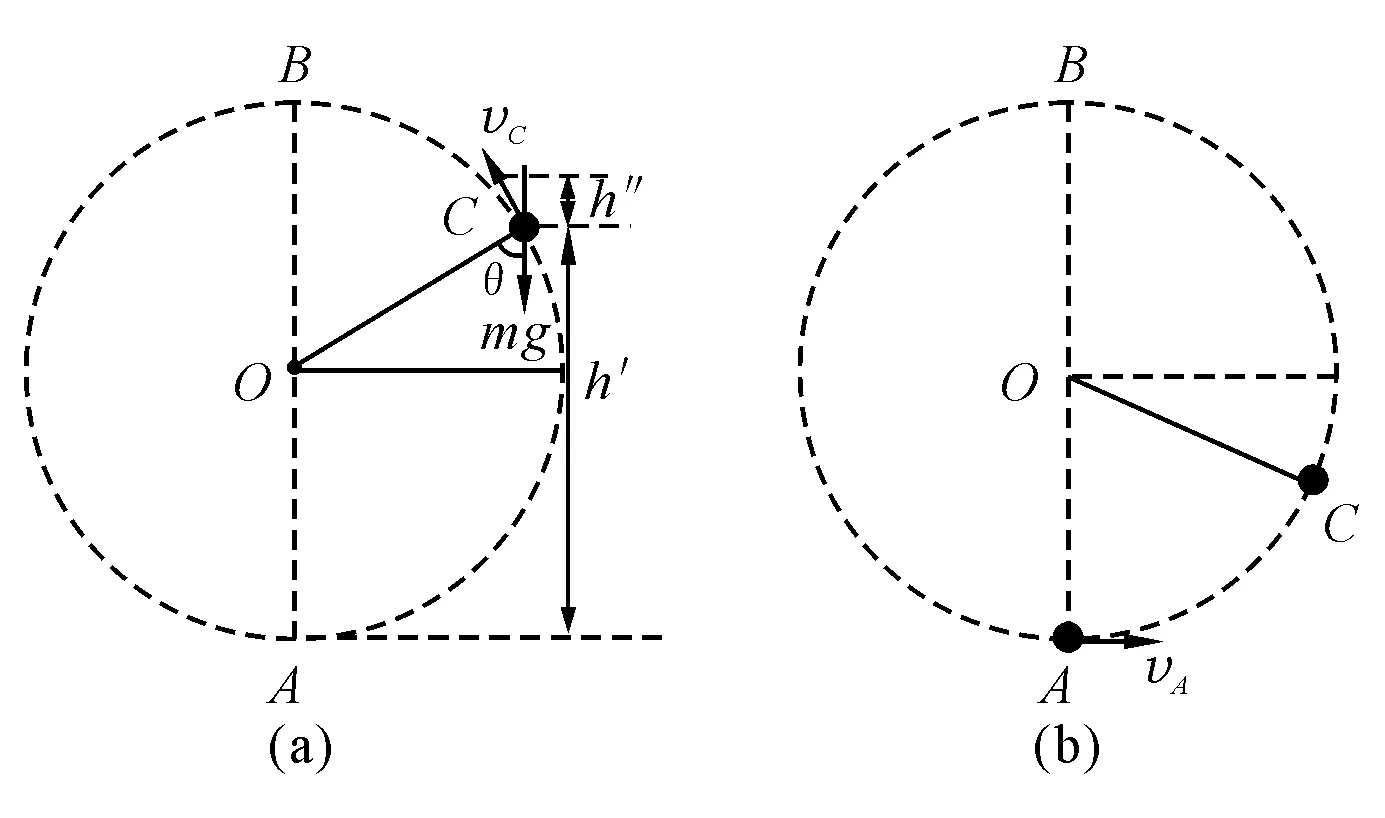
(3)由于h′ (3) (4) 聯立解得 圖2 解析:設物體在N處滿足彈力FN=0,設此時距頂點高度為h, 從頂點至N,由動能定理,有 (1) 在N處:FN=0有 (2) 而 (3) 由式(1)、(2)、(3)得 則有 (4) 【例3】用長為L=1.6 m的細繩,一端系著質量M=1 kg的木塊,另一端掛在固定點上.現有一顆質量m=20 g的子彈以v1=500 m/s的水平速度向木塊中心射擊,結果子彈穿出木塊后以v2=100 m/s的速度前進.求木塊能運動到的最高位置.(取g=10 m/s2,空氣阻力不計) 解析:木塊在向上運動的過程中,速度逐漸減小,有可能通過最高點B,也有可能不會通過B點,即木塊運動到某一臨界位置C時,若木塊所受的重力在沿半徑的分力恰好等于木塊做圓周運動所需要的向心力,此時繩子的拉力為零,繩子便開始松弛.如果C點在圓心O所在水平面以上[圖3(a)],木塊就以此刻所具有的速度vC做斜上拋運動.木塊所能到達的高度就是C點的高度和從C點開始的斜上拋運動的最大高度.如果C點在圓心O所在水平面以下[圖3(b)],即木塊的最高點在O點水平面下方時速度就減為零,此處即為物塊運動的最高點.由上分析可知,要先根據圓周運動的臨界條件判斷木塊的運動. 圖3 具體解答如下: 在水平方向動量守恒,有 mv1=MvA+mv2 (5) 式(5)中vA為木塊被子彈擊中后的速度,木塊被子彈擊中后便以速度vA開始擺動. 從式(5)求得 vA=8 m/s 設木塊剛好能擺動到了B點.則它在B點時的速度vB.應滿足方程 (6) 這時木塊的重力提供了木塊在B點做圓周運動所需要的向心力. 解上述方程得 vB=4 m/s 如果vB<4 m/s,則木塊不能升到B點,會在到達B點之前的某一位置以某一速度開始做斜向上拋運動,或者直接從該位置滑下,選A點為零勢能點,木塊在A點時的能量為 木塊在B點時的能量為 兩者不相等,可見木塊升不到B點;而物體在與圓心等高處的重力勢能為 Ep=MgL=16 J 所以物體上升的高度h滿足 1.6 m 設木塊在臨界位置C時的速度為vC,高度為h′如圖所示,則有 h′=L(1+cosθ) (7) 根據機械能守恒定律有 (8) 在C處,有 (9) 由式(7)、(8)、(9)得 所以 木塊從C點開始以速度vC做斜上拋運動所能達到的最大高度h″為 所以物體上升的最大高度為 通過對以上例題的分析,不難看出在變速圓周運動中的某些特殊位置上,常存在著最小(或最大)的速度,小于(或大于)這個速度,物體就不能再繼續做圓周運動了.通過對此類題型的分析,可以激發學生學習物理學的興趣,掌握物理學的基本規律,培養創造性思維.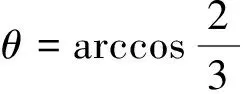
2 圓軌道外側的拋體運動
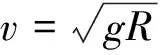
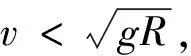
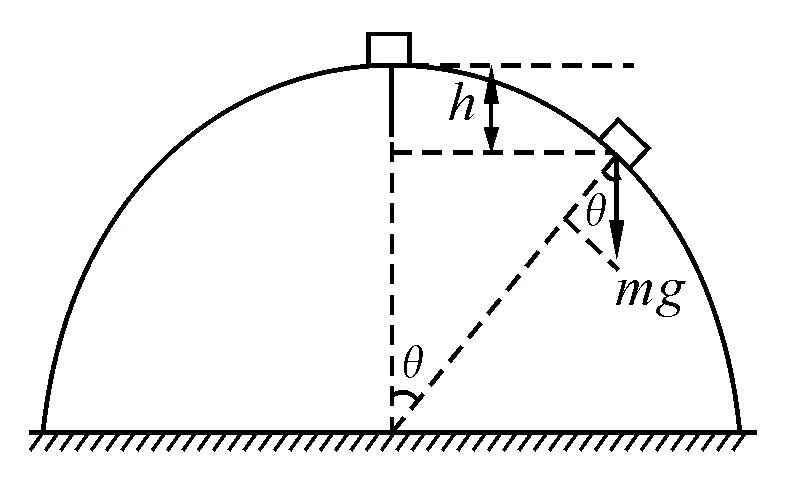
3 輕質繩作用下的拋體運動