海底隧道預注漿加固效果檢查與評價

汪 磊,李 濤,王全勝

(1.上海工程技術大學城軌學院,上海 201620;2.北京交通大學土建學院,北京 100044;3.中鐵隧道科研所,河南洛陽 471009)

注漿技術自從發明以來,已經廣泛地應用于封堵涌水和改良地層,在基礎建設的各個方面起到了良好的作用。而在海底隧道的修建中,由于環境的特殊性,裂隙巖體和無限量的海水補給使得隧道的安全施工更加特殊,隧道突涌水破壞或圍巖失穩都會帶來不可挽回的后果,因此，對于不良地質段隧道的施工往往采用預注漿對圍巖進行超前加固,但目前預注漿效果檢查技術很不規范,尚無完善的標準可以借鑒,繼而導致了一些注漿工作完成后無法正確評價,從而影響了注漿工程取得良好的效果。本文以青島膠州灣海底隧道斷層F4-4第一循環預注漿為背景,針對海底不良地質段隧道預注漿效果進行研究。利用理論公式法、數值法和現場實測的方法對涌水量進行計算和測定,比較它們之間的關系,分析其中的規律,得出海底隧道的實際注漿效果。

1 工程概況

青島膠州灣海底隧道是我國大陸第二條海底隧道,隧道南接黃島區的薛家島,北連青島團島,下穿膠州灣灣口海域,隧道全長6 170 m,其中海域段長3 950 m。隧道采用雙向雙洞六車道,中間設服務隧道,隧道主要采用鉆爆法施工。根據前期工程地質勘探的結果,隧道海域段基巖受構造運動影響較嚴重,破碎巖體及抗風化能力較低的輝綠巖脈較發育,對水敏感的Ⅳ～Ⅴ級圍巖所占比例較大,其中,隧道主洞II～III級圍巖約占55.7%,IV級圍巖約占38.1%,V級圍巖約占6.2%。隧道頂部25 m內巖體中的地下水活動痕跡普遍較明顯,隧道開挖時的爆破震動和圍巖松弛都可能使其透水性加劇,埋深不足25 m的海域段占了相當大的比例。

2 涌水量計算

2.1 涌水量理論計算

2.1.1 理論計算地質模型

斷層F4-4位于隧道YK6+915～YK6+961段,長46 m,高潮時水深27～30 m；海床呈緩坡狀。海底覆蓋層較薄,一般為2～3 m,主要為砂礫,局部沉積有淤泥。隧道拱頂覆蓋層24～26 m。基巖以含晶屑火山角礫凝灰巖為主,局部夾凝灰巖、并有較多輝綠巖脈、石英正長巖脈侵入。斷層F4-4為北西向破碎帶,帶內巖體為碎裂—鑲嵌碎裂結構,裂隙以密閉型為主,少數為微張型,裂隙面浸染跡象不甚明顯；圍巖在松弛變形時抗滲性能易惡化,還可能發生滲透變形破壞。注漿施工地段為斷層F4-4,相對位置如圖1所示。

考察相關地質資料,斷層F4-4為弱風化巖體受風化裂隙影響,具有弱～中等透水性,綜合滲透等級為中等透水。具體各層滲透系數見表1。

表1 海域巖土體滲透系數統計綜合成果

圖1 斷層F4-4相對位置示意

為了使所研究的海域段隧道穿越斷層F4-4更具有指導意義,具體計算位置為斷層F4-4的兩端和中間,即為YK6+915、YK6+938和YK6+961。

2.1.2 理論計算概化模型

根據地質模型,建立涌水量的理論計算模型。如圖2所示。當隧道圍巖含有兩種以上的含水層介質時,其滲透系數按下式進行等效化處理

(1)

式中，n、Mi、Ki分別為滲透性分層的數目、第i層的厚度和滲透系數。圖2中H為含水層中原始靜水位至隧道等價圓中心的距離，m；H0為含水體厚度，m；r為隧道洞身橫斷面的等價圓半徑，m；d為隧道洞身橫斷面的等價圓直徑，m。

圖2 涌水量計算概化模型示意

2.1.3 理論計算公式及結果

海底隧道位于半無限含水層中,地下水直接接受海水的定水頭入滲補給,施工前期的最大涌水量與施工中的經常涌水量基本一致。其最大涌水量的計算公式如下。

(1)大島志洋公式(模型1)

(2)

式中，q0為單位長度可能最大涌水量，m3/d·m；K為巖層滲透系數；H為含水層中原始靜水位至隧道等價圓中心的距離，m；r為隧道洞身橫斷面的等價圓半徑，m；d為隧道洞身橫斷面的等價圓直徑，m；m為轉換系數,一般取0.86。

(2)鐵路規范古德曼經驗式(模型1)

(3)

式中，q0為單位長度最大涌水量，m3/d·m；K為滲透系數，m/d；H為靜止水位至洞身橫斷面等價圓中心的距離，m；d為隧道洞身橫斷面等價圓直徑，m。

(3)鐵路規范經驗式(模型2)

q0=0.025 5+1.922 4K·H

(4)

式中，q0為單位最大涌水量，m3/d·m；K為滲透系數，m/d；H為含水體厚度，m。

(4)注漿后涌水量計算公式

(5)

式中，Q為單位最大涌水量，m3/d·m；Ki為注漿區域滲透系數，m/d；K為巖體滲透系數，m/d；h為含水層中原始靜水位至隧道等價圓中心的距離，m；R為隧道等效半徑，m；t為注漿加固圈厚，m。

利用如上4個公式計算結果分別如表2～表5所示。

表2 海域隧道(右洞)涌水量計算(大島洋志公式)

表3 海域隧道(右洞)涌水量計算(鐵路規范古德曼經驗式)

表4 海域隧道(右洞)涌水量計算(鐵路規范經驗式)

表5 海域隧道(右洞)涌水量計算(注漿后)

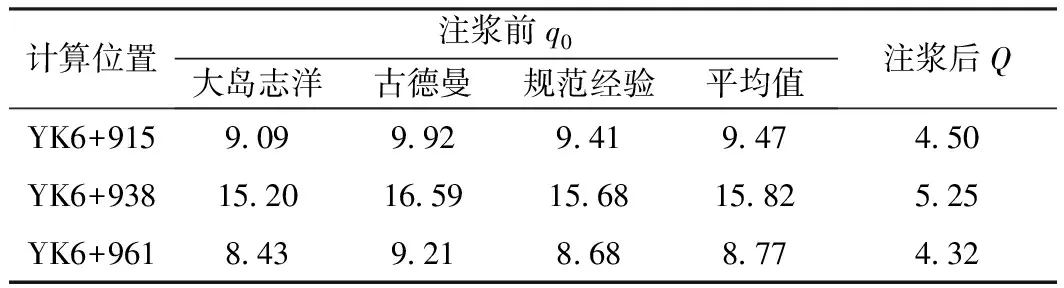
表6 海域隧道(右洞)最大涌水量對比 m3/d·m

分析表6,在斷層F4-4地段隧道右洞沿線的涌水量計算時用不同的公式計算所得結果有所不同,用大島洋志公式計算的涌水量最小,鐵路規范古德曼經驗式計算的涌水量最大,鐵路規范經驗式計算的涌水量居中。不過總的來說,三者結果相差不大,斷面YK6+915涌水量大約為9.47 m3/d·m；斷面YK6+938涌水量大約為15.82 m3/d·m；斷面YK6+961涌水量大約為8.77 m3/d·m。

根據注漿后試驗測得,注漿體的滲透系數大約為1.0×10-5cm/s,利用公式(5)可得注漿后的涌水量結果如表5所示,并將其與注漿前的涌水量進行比較可知,通過注漿后隧道涌水量明顯降低,由于在過同一個斷層F4-4的時候使用的是同樣的注漿結束標準,所以注漿結束后注漿體的滲透系數相似,進而注漿后各個斷面上的涌水量也相近。

2.2 涌水量數值計算

2.2.1 數值計算概化模型

為了與理論公式及經驗公式的計算結果進行對比,數值法計算仍取在斷層F4-4范圍即隧道YK6+915～YK6+961段內的兩端和中間的3個斷面進行模擬計算。具體位置分別為YK6+915、YK6+938和YK6+961,其中在斷面YK6+915和斷面YK6+961計算的涌水量代表斷層兩頭處隧道內的涌水量情況,而在斷面YK6+938所計算的涌水量代表斷層中間處的涌水量情況。另外,不考慮雙洞滲流效應,僅考慮右線隧道斷面內的涌水量情況。計算剖面1見圖3(其他2個剖面類似),其中水平向取200 m,豎向取100 m(不包括海水部分)。

圖3 剖面1(YK6+915)(單位：m)

YK6+915、YK6+938和YK6+961 3個剖面均為海域剖面,左右兩側及頂部均有水源補給,而且認為所選計算范圍足夠大,因此可以視為定水頭邊界,水頭值等于海平面所對應的位置高程(即水頭),為承壓滲流場。另外,由于隧道處巖體的滲透性較差,地下水以滲出的形式涌出,因此隧道內側可作為第一類邊界(自由滲出面)加以模擬；隧道底部邊界以下地下水呈水平滲流狀態,對隧道涌水量影響較小,視為第二類邊界條件(零流量邊界)。

2.2.2 數值計算理論基礎

單位厚度的隧道涌水量理論計算公式如下

(6)

式中,L為隧道周邊輪廓；n為隧道壁法線方向；其他參數意義同前。

實際計算中,作如下簡化：用隧道壁4個特征點(頂點、左側點、底點、右側點)(圖4)位置處的單寬流量的平均值代表整個隧道壁的單寬流量Q0,Q0與隧道周長L的乘積即為單位厚度隧道涌水量。

圖4 隧道涌水量計算點示意

2.2.3 數值計算分析

為了分析考慮隧道穿越F4-4斷層時預注漿加固前后涌水量的比較,考慮了3種工況進行分析：

(1)無預注漿加固時,考慮滲流場作用下隧道涌水量的計算；

(2)采用不同的預注漿加固圈厚度(分別取3、4、5、6、7 m和8 m)時,考慮滲流場作用下隧道涌水量的計算,其中設圍巖滲透系數Kr與注漿圈滲透系數Kg,令Kr/Kg=2、Kr/Kg=5和Kr/Kg=10；

(3)采用設計注漿加固圈厚度為5 m,令Kr/Kg=2、Kr/Kg=3、Kr/Kg=4、Kr/Kg=5、Kr/Kg=6、Kr/Kg=7、Kr/Kg=8、Kr/Kg=9和Kr/Kg=10時,考慮滲流場作用下隧道涌水量的計算。

膠州灣海底隧道預注漿加固圈的設計厚度為5 m,但對于不同的注漿剖面所取得的注漿效果也不同,主要由于所注圍巖的地質特征不同,進而表現為隧道開挖時的涌水量不同。如圖5為當注漿加固圈厚度為5 m時,采用不同的注漿圈滲透系數可以計算出不同的日涌水量。對于剖面1和剖面3當Kr/Kg>5后,隧道開挖涌水量的計算結果減少變緩；對于剖面2當Kr/Kg>7后就會出現隧道開挖涌水量的計算結果減少變緩的現象。

圖5 隧道開挖涌水量隨注漿圈滲透系數的變化

圖7 檢查孔布置

當所取注漿圈的滲透系數相同而注漿圈厚度不同時,計算所得隧道開挖日涌水量也不相同。如圖6分別為剖面1(其他2個剖面類似)在隧道開挖涌水量隨注漿圈厚度的變化情況,計算中分別考慮了Kr/Kg=2、Kr/Kg=5和Kr/Kg=10 3種情況。從圖中可以看出，這3種情況下隧道開挖涌水量隨注漿圈厚度變化的規律是相似的,并且當注漿圈厚度大于5 m后,隧道開挖日涌水量的變化逐漸趨緩并最終趨向于穩定。

圖6 剖面1隧道開挖涌水量隨注漿圈厚度的變化

同時,當注漿圈從3 m增加到8 m的過程中在各個滲透系數確定的情況下,隧道開挖日涌水量的變化值也是幾乎相同的。這就可以說明對于同一滲透系數,注漿圈厚度的改變對隧道開挖日涌水量的控制是有限的,所以對于一定的隧道圍巖地質狀況,當注漿材料、注漿工藝等確定時,必需注意控制注漿效果,避免浪費。

3 海底隧道預注漿檢查

此循環總注漿量為1 285.4 m3,總進尺為30 m,平均每延米注漿量為42.85 m3。單孔最大注漿量為0.51 m3/m,主要集中在隧道開挖面的上部和左側,此處裂隙較大,出水量較大；右側孔(地質情況較好)出現最小注漿量0.2 m3/m。

注漿分多次掃孔完成,注漿主要是填充裂隙加固巖層。拱頂部位是注漿的關鍵,從地質探孔和注漿鉆孔情況分析,拱頂正上方5 m,而這一位置恰好處于B續孔端部,為注漿加固之薄弱環節。拱頂A5、A6、B3、C1、C3等孔注漿量也較大,達到0.4～0.51 m3/m,在這4個孔中掃孔至7 m開始有較大出水量,在第二次補充注漿掃孔后無水或水量很小,但注漿量依然很大,注漿壓力很低(1 MPa左右),上升緩慢甚至注漿量達到設計值而壓力無法達到設計值。通過反復分析掃孔和注漿過程,在拱頂正上方偏左1～3 m,深度為17～20 m位置處有結構面,存在較大的裂隙,通過注漿已完全封堵了此裂隙。

此循環注漿為擠密注漿,注漿過程控制采用“控壓限量”的方法,注漿壓力限制在3～4 MPa內,主要以控制注漿壓力及流量作為單孔每循環注漿結束標準。

3.1 注漿檢驗孔布置

注漿效果檢查采用鉆檢查孔法,根據注漿狀況,選擇注漿范圍存在薄弱環節的注漿部位布設檢查孔,檢查孔布置如圖7所示。

3.2 實測涌水量統計(表7)

表7 檢查孔出水量匯總 L/min

分析如上各孔的出水量,總共出水量為1.49 L/min。其中,J2、J3和J4出水量較大,J7、J8出水量較小,可以說明隧道左側裂隙較發育,出水量較大,這和前面整個斷面內的注漿量分布是相對應的。為了進一步研究出水量在注漿前后的分布規律，下面將綜合公式法和數值法對涌水量進行計算。

4 涌水量計算比較及分析

4.1 無注漿情況下隧道開挖涌水量計算比較

在無注漿情況下,利用公式法和數值法的隧道開挖涌水量計算結果如表8所示。

表8 無注漿情況下隧道開挖涌水量計算結果 m3/d

通過分析表8可以發現，在剖面1和剖面3利用公式法計算的結果較數值法小一些,而在剖面2正好相反。分析兩種計算方法,對于公式法,它有很多的不足,比如說：只能考慮圍巖滲透系數為各向同性；只能對圓形洞室進行求解；大部分公式只是對毛洞進行研究，不能考慮注漿、襯砌結構等的影響；不能考慮滲流場和應力場等的耦合作用。而對于數值法,在求解邊界條件復雜、本構關系復雜的問題上有很大的優勢,但它的計算結果有很大的隨意性,仍然有它的不足,其中涌水量的計算結果受所取滲透系數、計算模型大小、網格劃分質量等條件影響很大。另外,就計算的3個剖面而言,3個剖面所對應的地質情況不相同,計算所得滲透系數也不同,其中在數值法計算中隧道圍巖的滲透系數是按公式等效后選用的,而在這個等效化公式中涉及到了模型尺寸,所以即使對于同一計算剖面,而選用不同的計算模型就會得出不同的等效化滲透系數,進而計算出不同的涌水量。即而會出現剖面1和剖面3利用公式法計算的結果較數值法小一些,而剖面2正好相反的情況。

4.2 注漿情況下隧道開挖涌水量計算比較

比較公式法和數值法在注漿后的隧道開挖涌水量見表9,一方面注漿后的比較結果和注漿前的比較結果是一樣的；另一方面,剖面1和剖面2的計算結果相似的。所以在實地注漿的時候,注漿設計時可以將Kr/Kg=5所對應的注漿量作為實際設計值進行參考,而剖面2的注漿量Kr/Kg=5所對應的注漿量及注漿壓力基礎之上應該有所提高,才能充分達到預期的注漿效果。

表9 注漿后隧道開挖涌水量計算結果 m3/d

4.3 與實測數據的比較

過斷層F4-4的第一個循環預注漿,即隧道過斷層F4-4的開始段,與計算模型的剖面1相對應。根據實測結果,此次注漿循環后隧道上半斷面10個檢查孔總共的出水量為2.145 6 m3/d。10個檢查孔的出水量僅為上隧道上半斷面的涌水量值,如果近似考慮隧道上半斷面和下半斷面的涌水量相等,整個隧道開挖出水量大約為4.29 m3/d,而用數值分析法和公式法的計算結果分別為4.35 m3/d和4.50 m3/d。因此可以說明,此循環注漿達到了預期設計目的。

5 結論

通過隧道開挖涌水量計算和注漿后隧道出水量實測兩方面對海底隧道穿越斷層F4-4時預注漿的效果進行檢查與評價,可以得出如下結論。

(1)公式法計算隧道開挖涌水量有很多的不足,主要是由于公式法的一些假設與實際隧道圍巖的地質情況有一定的差距；數值法在求解邊界條件復雜、本構關系復雜的問題上有很大的優勢,涌水量計算結果較為合理,在計算過程中需特別注意滲透系數的選取、計算模型大小、網格劃分質量等條件。

(2)比較兩種方法的計算結果可知,基本上利用數值法的計算結果要大于公式法的計算結果,原因主要在于數值法考慮的隧道圍巖地質特性和隧道斷面形狀與實際更符合些。

(3)當采用不同注漿圈厚度和不同注漿圈滲透系數時,隧道開挖涌水量的變化明顯有一定的規律,主要表現為兩方面：一方面,隨著注漿圈厚度的增加隧道開挖涌水量減小,但當注漿圈厚度大于5 m后,3個剖面的隧道開挖涌水量的變化趨于平緩。如果按注漿圈厚度為5 m和Kr/Kg=5時進行比較,3個剖面的涌水量分別為4.35、9.33、4.20 m3/d,而在未注漿的情況下,三者分別為9.11、17.40、7.35 m3/d,即涌水量分別減少了54%、46%和43%。另一方面,在相同注漿圈厚度的情況下,隨著注漿圈滲透系數的減小,隧道開挖涌水量也相應的減小,但對于不同的隧道圍巖地質,當注漿圈滲透系數小于一定值的時候,隧道開挖涌水量的減少就會變得不明顯。當Kr/Kg=5時,相對于未注漿隧道的涌水量減小了54%,并且會隨著Kr/Kg值的增大涌水量會進一步減少,但變化會越來越小。

(4)通過如上計算過斷層F4-4開始階段時,用公式法、數值法及實測所得的隧道涌水量分別為：4.50、4.35、4.29 m3/d,三者大小相近,說明本循環注漿達到了設計預期目標。

[1]王建秀,朱合華,葉為民.隧道涌水量的預測及其工程應用[J].巖石力學與工程學報,2004,23(7):1150-1153．

[2]丁萬濤,李術才,徐幫樹，等.隧道涌水量解析公式在海底隧道工程應用研究[J].地下空間與工程學報,2008,4(4):662-664．

[3]劉繼國,朱光儀,郭小紅，等.廈門海底隧道建設中涌水量流固耦合數值模擬[J].現代隧道技術,2006,43(2):34-38．

[4]姬永紅,項彥勇.水底隧道涌水量預測方法的應用分析[J].水文地質工程地質,2005(4)：84-87．

[5]李廷春,李術才,陳衛忠，等.廈門海底隧道的流固耦合分析[J].巖土工程學報,2004,26(3):397-401．

[6]畢煥軍.裂隙巖體數值法預測計算特長隧道涌水量的應用研究[J].鐵道工程學報,2000(1)：59-62．

[7]許巧詳,劉 斌,金 明,等.地鐵隧道穿越江河地質穩定性及滲流特性數值分析[J].中國安全生產技術,2007,3(1):62-65.

[8]Manuel M, Luis M, Jose M. Prediction and analysis of subsidence induced by shield tunneling in the Madrid metro extension. Canada. Geotech J., 2002,39:1273-1287.

[9]Hakami H. Rock characterisation facility (RCF) shaft sinking numerical computations using FLAC[J]. International Journal of Rock Mechanics and Mining Sciences, 2001,38(1):59-65.

[10]李昌寧.廈門海底隧道施工中重難點分析及技術措施[J].鐵道標準設計，2007(S2):1-4.

[11]汪小平.廈門東通道海底隧道涌水量分析及預測[J].鐵道勘察,2008(1)：27-29．