布爾函數的代數攻擊
楊文峰,胡予濮,高軍濤
(西安電子科技大學計算機網絡與信息安全教育部重點實驗室 西安 710071)
布爾函數的代數攻擊
楊文峰,胡予濮,高軍濤
(西安電子科技大學計算機網絡與信息安全教育部重點實驗室 西安 710071)
基于代數攻擊,提出了一種已知部分真值表還原整個布爾函數的方法。對于n元d次布爾函數, 該方法的空間復雜度和數據復雜度均為O(N),計算復雜度為O(N3),其中。由復雜度可知,所求密碼函數的代數次數越低,該方法的有效性越高。攻擊方法表明密碼設計中應該謹慎使用代數次數較低的布爾函數。
代數方法; 布爾函數; 密碼分析; 密碼學
作為許多流密碼的核心部件,布爾函數的設計和分析一直是密碼學中極為活躍的研究領域。在密碼算法設計中,設計者通過構造滿足各種密碼學指標的布爾函數以增加密碼的強度。而在密碼分析中,攻擊者往往通過尋找并利用布爾函數的設計漏洞和弱點實現對密碼算法的攻擊。密碼設計者和攻擊者這種堅持不懈的攻防爭斗正是密碼學發展的源動力所在[1-3]。各種密碼攻擊方法的不斷出現迫使布爾函數的設計必須滿足多方面的指標,而各種指標之間的相互制約關系往往又為攻擊者尋找新的攻擊方法提供了機會。本文提出的攻擊方法就是一個基于該攻擊思想的實例。
在流密碼分析中,攻擊者常常會遇到以下兩種情形:一種情形是攻擊者無法通過公開途徑獲得密碼算法,盡管文獻[4]指出流密碼的安全性不應該依賴于密碼算法的保密性,而應僅依賴于密鑰的保密性,但實際中使用的流密碼算法往往是不公開的[1]。另一種情形是密碼算法使用的布爾函數是由密鑰控制的[5]。對于這兩種情形,攻擊者的任務是不但要恢復密鑰而且必須恢復布爾函數。密碼分析過程中,布爾函數的恢復往往都是利用統計方法求取其真值表。統計方法的致命弱點是所需數據量巨大,使得攻擊者往往因為數據量有限而只能求得布爾函數的部分真值表。因此,如何通過布爾函數的已知部分特性恢復出完整的布爾函數具有現實的應用背景。代數攻擊思想[6-7]和布爾函數指標之間的內在制約關系為本文提供了一種基于部分真值表的布爾函數還原方法。只要布爾函數真值表的已知部分包含了確定該函數的所需的全部或者接近全部信息量,本文的攻擊方法可以唯一確定該函數的代數表達式。布爾函數的代數表達式和真值表之間存在著一一對應關系,求出代數表達式就等于確定了所求的布爾函數。
1 密碼學中的布爾函數
首先給出布爾函數的定義和兩種表示方法,然后討論布爾函數的相關密碼學指標,最后闡述本文的攻擊思路。

布爾函數主要有真值表表示、小項表示、多項式表示和Walsh譜表示4種表示方法。本文只考慮真值表表示和多項式表示。

多項式表示法則是指任意n元布爾函數f(x)都可用其代數表達式表示為:
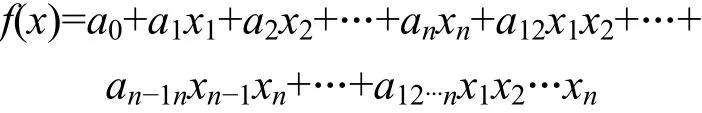
布爾函數的各種表示方法之間是相互等價的,只要知道了其中的一種表示方法就可以唯一確定其他的表示方法。
為了防止已知的各種攻擊方法,密碼學中使用的布爾函數必須滿足一定的密碼學指標,其中主要有次數(代數次數和非線性次數)、均衡性、相關免疫性、嚴格雪崩準則和擴散準則等。已有的研究結果表明,布爾函數各項指標之間是相互沖突、相互制約的,所以密碼設計者總是無法設計出各項指標都能達到最優的布爾函數。由于攻擊者是尋求利用布爾函數的最弱的一點采取攻擊,這就使得設計者設計布爾函數時不得不采取各項密碼學指標折衷的思想。充分挖掘利用密碼學指標之間的制約關系正是解決本文中問題的基本思路。
n元均衡布爾函數f(x)的代數次數d和相關免疫階m就存在著嚴格的制約關系,即如下定理。
定理 1[8]若n元d次布爾函數f(x),x∈GF(2)n是m階相關免疫的,則d+m≤n;若更設f(x)是均衡的,且1≤m≤n?2,則d+m≤n?1。
由上述定理可以看出,布爾函數的代數次數d必須滿足d≤n?1?m,即布爾函數的相關階m越大,代數次數d就越小。當設計者為了防止相關攻擊[9-10]而不得不提高布爾函數的相關免疫階和犧牲布爾函數的次數時,就為利用布爾函數的部分真值表還原整個布爾函數提供了有利條件。只要已知的部分真值表中包含了d(d≤n?1)次布爾函數的全部信息,應用代數攻擊的思想首先求出該函數的代數表達式,然后把真值表中未知函數值的自變量代入代數正規型就可以補全其真值表。
2 攻擊方法
代數攻擊[6]是一種密碼分析方法,常用于對流密碼、分組密碼及HFE公鑰密碼系統的安全性分析。代數攻擊方法的步驟為:(1)通過分析利用密碼算法的代數結構,把密碼算法的安全性(密鑰恢復)規約為一個次數盡可能低的超定多元方程組的求解問題;(2)求解步驟(1)中的多元高次方程組,代數攻擊的復雜度主要取決于多元方程組的求解復雜度,現有的求解方法主要有Linearization、Relinearization、XL、Gr?bner Base等;(3)如果步驟(2)中順利求出了多元方程組的解,結合步驟(1)中分析的密碼算法的代數特征,密碼算法的安全性就無法保證。
從上述代數攻擊的基本思想可以看出,所謂的代數攻擊實際上就是一個利用密碼系統的代數結構建立方程組進而求解的過程。本文的攻擊方法就是利用布爾函數的部分真值表和代數表達式建立一個(線性)方程組,然后求解方程組得到代數表達式的系數。主要分為以下3個步驟。

如果根據真值表的已知部分和上述代數表達式能夠確定出多項式的系數a0、a1、…、an?d+1…n,就求出了布爾函數。
2)建立多元線性方程組,根據真值表中已知的函數值,把對應的自變量和函數值分別代入步驟1)的布爾函數的代數表達式,得到一個包含M個線性方程的多元線性方程組。
3)求解線性方程組,利用Gauss消元法對步驟2)中得到的線性方程組進行化簡求解。假設方程組中含有Q個線性無關的方程,求解的結果有4種情況。
(1)Q (2)Q (3)Q=N。說明該布爾函數的代數次數正好為d并且真值表中包含所求布爾函數的信息量足夠唯一確定布爾函數。 (4)Q>N。說明所求布爾函數的代數次數大于d,利用已在的真值表無法確定該布爾函數。 該攻擊方法實現簡單,計算復雜度低,有利于工程實現。攻擊方法的主要計算就是用Gauss消元法求解一個線性方程組,其計算復雜度就是Gauss消元法的計算復雜度,即O(N3)。對于n元d次布爾函數來說由于方程組中未知元的系數是由1、x1、x2、…、xn、x1x2、…、xn?1xn、…、xn?d+1xn?d+2…xn組成的,輸入變量的相互糾纏使得方程組中的線性無關的方程個數不能精確計算,也就無法給出唯一確定布爾函數的M的精確估計。但可以利用布爾函數的理論給出M的上下界。由攻擊方法易知M的下界就是N。 定理 2[8]任意兩個不同的次數小于等于d的n元布爾函數的漢明距離至少為2n?d。 由上述定理可知M的上界就是2n?d。 舉例說明攻擊方法的有效性。假設已知8元布爾函數的部分真值表如下(自變量按照 x8,x7,x6,x5,x4,x3,x2,x1的字典序排列): 得到d=4。由此可以確定如果該布爾函數的代數次數d≤4,通過本文的攻擊方法就可基本求出函數的代數表達式;如果d>4,本攻擊方法無效。假設所求布爾函數的代數表達式為: 攻擊的目的就是求出上述代數正規型中的所有系數a0、a1、a2、…、a8、a12、…、a78、…、a5678。 根據攻擊方法中的步驟(2),把真值表中有函數值的x和f(x)代入上述代數表達式,得到一個包含163個線性方程的線性方程組。 接下來實施攻擊方法中的步驟(3),利用Gauss消元法化簡上述方程組后,獲得的方程組的秩為162,該方程組有一個自由變量a5678,這屬于攻擊方法中的第二種情形。通過窮舉自由變量a5678得到兩個布爾函數的代數表達式分別為: 從已知的真值表所能提供的信息量看,應用本文的攻擊方法無法確定所求布爾函數的代數表達式是f1(x)還是f2(x)。但是結合其他信息,例如流密碼的簡潔性原則或者密碼學中布爾函數設計的經驗,不難看出: 其中邏輯函數φ(x6,x7,x8)的真值表如表1所示。 表1 邏輯函數φ(x6,x7,x8)的真值表 這就是著名的Maiorana-McFarland函數[11-12]。由此可以得出,f1(x)即為所求的布爾函數。當然,這只是對所攻擊的布爾函數一種判斷方法,最終正確與否還要結合密碼攻擊的實踐進行判斷。 流密碼的安全往往取決于其密鑰流生成器中布爾函數的設計質量。在未知密碼算法或者由密鑰控制布爾函數的流密碼分析過程中,布爾函數的恢復是首先要解決的問題。另外,密碼分析中的許多問題都可以轉化為布爾函數的分析。當攻擊者占有的數據有限時,只能求出部分真值表。本文利用布爾函數的次數和相關免疫階的制約關系提出了一種基于代數攻擊思想的布爾函數還原方法。當已知的部分真值表包含所求布爾函數的全部信息時,該方法就可以唯一確定布爾函數。攻擊方法的計算復雜度低,實現簡單。但該攻擊方法的復雜度與布爾函數階的關系、小項數及其分布的關系等如何給定嚴格的界限,還有待進一步研究。 [1]KAHN D. The codebreakers: the story of secret writing[M].New York: Macmillan, 1967. [2]汪小芬, 李勝強, 肖國鎮. 認證群密鑰協商協議的安全性分析與改進[J]. 電子科技大學學報, 2009, 38(1): 51-54. WANG Xiao-fen, LI Sheng-qiang, XIAO Guo-zhen.Analysis and improvement of an authenticated group key agreement protocol[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(1): 51-54. [3]ZHANG J L, WANG Y M. Efficient membership revocation in ACJT group signature[J]. Journal of University of Electronic Science and Technology of China, 2008, 6(1): 39-42. [4]SCHNEIER B. Applied cryptography second edition:protocols, algorithms, and source code in C[M]. [S.l.]: John Wiley & Sons, 1996. [5]GOLI? J D, MORGARI G. On the resynchronization attack[C]//Proceedings of FSE’03, LNCS 2887. Berlin:Springer-Verlag, 2003: 100-110. [6]COURTOIS N T, MEIER W. Algebraic attacks on stream ciphers with linear feedback[C]//Proceedings of Eurocrypt’03, LNCS 2656. Berlin: Springer-Verlag, 2003: 345-359. [7]COURTOIS N T. Fast algebraic attacks on stream ciphers with linear feedback[C]//Proceedings of Crypt’03, LNCS 2729. Berlin: Springer-Verlag, 2003: 176-194. [8]CLARLET C. Boolean functions for cryptography and error correcting codes[DB/OL]. [2009-9-10]. http://www-rocq.inria.fr /secret/Claude.Carlet/chap-fcts-Bool.pdf. [9]SIEGENTHALER T. Decrypting a class of stream ciphers using ciphertext only[J]. IEEE Transactions on computers,1985, 34(1): 81-85. [10]MEIER W, STAFFELBACH O. Fast correlation attacks on stream ciphers[C]//Proceedings of Euro-crypt’88, LNCS 330. Berlin: Springer-Verlag, 1988: 301-314. [11]GUPTA K C, SARKAR P. Efficient representation and software implementation of resilient Maiorana-McFarland S-boxes[C]//Proceedings of WISA’04, LNCS 3325. Berlin:Springer-Verlag, 2004: 317-331. [12]CLARLET C. A larger class of cryptographic Boolean functions via a study of the Maiorana-McFarland construction[C]//Proceedings of Crypt’02, LNCS 2442.Berlin: Springer-Verlag, 2002: 549-564. 編 輯 稅 紅 Algebraic Attack on Boolean Functions YANG Wen-feng, HU Yu-pu, and GAO Jun-tao (Key Laboratory of Computer Networks and Information Security Ministry of Education, Xidian University Xi'an 710071) Based on algebraic attack, a new reconstruction method of Boolean functions from the partial truth table is proposed. For the Boolean function with n variables and the degree of d, the proposed method requires O(N)values in the truth table, and the computational complexity is O(N3), and the memory complexity is O(N), whereFrom the above complexity, the lower the degree of the Boolean function is,the more efficient the method is. The proposed attack shows the designer of stream cipher should use Boolean functions with low degree carefully. algebraic approach; Boolean function; cryptanalysis; cryptology TN918.1 A 10.3969/j.issn.1001-0548.2010.06.006 2009- 04- 10; 2009- 07- 08 國家自然科學基金(60833008,60803149);國家973計劃(2007CB311201) 楊文峰(1971- ),男,博士生,副教授,主要從事密碼學方面的研究.3 攻擊實例

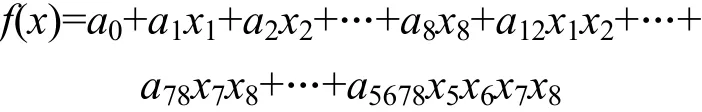



4 結 束 語

