基于靈敏度分析的改進遺傳算法
李建福,陳義保
(煙臺大學 機電汽車工程學院,山東煙臺 264005)
遺傳算法是上個世紀70年代由美國密執安大學的Holland教授提出的[1],是一種基于自然遺傳和自然選擇機理的全局尋優搜索方法。因為具有簡單通用、魯棒性強、適于并行處理以及高效、實用等顯著特點,所以其在各個領域得到了廣泛應用,取得了良好效果,并逐漸成為重要的智能算法之一。但在實際應用過程中,遺傳算法也暴露出了一些自身所固有的缺點,比如容易早熟、局部尋優能力差、求解精度不高等。
傳統的遺傳算法,可以很快到達最優解的90%左右[2],但是要達到最優解,往往還需要大量的時間,也就是遺傳算法具有較強的全局搜索能力,但是其局部搜索能力不強。本文提出的基于靈敏度分析的改進遺傳算法,將目標函數提供的導數信息加入到算法的搜索過程中去[3],使種群中的優秀個體,能按照指定的方向繼續進化,有效地提高了算法的局部搜索能力。同時,在該算法中融入了小生境技術,其應用有效地保持了種群的多樣性,提高了全局搜索能力,避免陷入局部最優解。
1 算法策略
1.1 小生境算法
小生境是指在特定環境中一種組織的功能,而把有共同特性的組織稱為物種。該技術就是將每一代遺傳個體分成若干類,從每個類中選出若干適應度較大的個體,作為一個類的優秀代表組成一個種群,再在種群中以及不同的種群之間通過雜交、變異,產生新一代個體群。本文使用的是基于排擠的小生境算法[4],其基本思想是依據個體之間的相似性,將種群分為若干個小生境,并排擠掉同一小生境中的較差的個體。這樣,各小生境中的最優個體,便可以認為是局部最優解鄰域內的一點。個體之間的相似性,用編碼串之間的海明距離來度量:

很顯然,dij越小,Xi和 Xj的相似程度就越大;dij越大,Xi和Xj的相似程度就越小。如果dij<L (L為設定的一較小的正數),也就說明它們屬于同一小生境,那么就對適應度較小的施加較強的懲罰函數Fmin=Penalty,其中Penalty為一個很小的正數。在基本遺傳算法運行的后期,小生境技術的融入,能克服適應度高的個體大量繁殖而充滿整個群體的缺陷,避免早熟現象的發生,保證了種群的多樣性及對整個解空間的搜索。
1.2 敏度分析原理
靈敏度就是導數信息,從數學意義上講,它反映了函數對某些自變量xi的變化梯度,若函數F(x)可導,其一階靈敏度S在連續系統中,可表示為S=F(x)/xi;在離散系統中,可表示為S=ΔF(x)/Δxi,分別為一階微分靈敏度和一階差分靈敏度[5]。當前靈敏度計算方法主要有3類:解析法、差分法和兩者混合的半解析法。解析法精度有保證,差分法和半解析法求解過程簡單,易于工程實現。
在遺傳算法中引入目標函數的導數信息,就可以通過靈敏度向量所指的方向尋找最優解,如果設問題的目標函數為f(x),種群中個體維數為m,那么目標函數f(x)的m維靈敏度向量可以表示為:

如果該向量方向始終指向增長方向,說明該方向是指向最大值,那么朝相反的方向移動則得到極小值,即:

如果該向量方向指向下降的方向,說明該方向是指向最小值,那么沿著該方向移動便得到最小值:

其中,η稱為步長,是一個很小的正數。
在實際應用中,由于某些目標函數不具有可導性,有些甚至無法寫出數學表達式,因此目標函數的導數信息往往不能用解析式表達出來。為了簡便起見,本文將利用目標函數的一階偏微分,來近似地代替其導數信息,即表示為:

對群體中每個小生境的最優個體進行基于靈敏度向量的局部尋優,就能使個體向局部最優解不斷地靠近,從而增強了算法的局部搜索能力,提高了算法的計算精確度,具體步驟如下:

else個體X已經到達了峰值。
2 遺傳算子
2.1 選擇算子
輪盤賭選擇法是一種回放式隨機采樣方法,也是遺傳算法中最早被提出來的一種方法。因為這種方法簡單而且實用,所以被廣泛使用。但由于隨機操作的原因,這種選擇方法的選擇誤差比較大,有的時侯甚至會出現“退化”現象,這樣便使適應度較高的個體失去了選擇機會。因此本文選用了一種改進的多輪輪盤選擇算子[6],改進的選擇算子每產生M個隨機數來確定一個個體,取代了傳統輪盤賭算子中的每產生一個隨機數確定一個個體,這樣產生隨機數的數量由原來的M增至M2,使隨機數的作用體現的更精確,從而降低了隨機操作所產生的誤差,提高了算子的選優能力,確保了優秀的個體能夠存留下來。
2.2 交叉算子
交叉運算是產生新個體的主要方法,它決定了遺傳算法的全局搜索能力。為了提高算法的全局搜索能力,本文采用算術交叉算子[7]。交叉后一點落于進行交叉的父代之間,另一點落于靠近較好父代的一側,使解能朝著較好的方向發展。自適應交叉系數,能使交叉量隨著進化代數的增大而減小。在算法中隨機選取兩個交叉個體Xi和Xj,先比較這兩個個體的適應度值F(Xi)和F(Xj),在這里我們可以假設F(Xi)>F(Xj),交叉點選為xik和xjk,那么交叉結果可以表示為:

其中

a0為預定系數;
t為當前進化代數;
T為最大進化代數;
Nk為取值范圍的上限;
Mk為xik取值范圍的下限。
2.3 變異算子
變異運算雖是產生新個體的輔助方法,但也是必不可少的一個步驟,決定了遺傳算法的局部搜索能力。為了增強算法的局部尋優能力,本文引入非均勻變異算子,重點搜索原個體附近的微小區域。如果變異個體設為X,變異點設為xi,取值范圍為[Nk,Mk],那么變異結果由下式決定:

式中
△(t,y)=y·(1-r(1-t/T)b),△(t,y)表示[0,y]范圍內符合非均勻變異的一個隨機數;
r為[0,1]范圍內的符合均勻分布的一個隨機數;
T為最大進化代數;
b為一個系統參數。
由此可見,該算法在進化的初始階段,將近似地進行均勻隨即搜索,隨著進化的延續,到了后期該算法將重點搜尋個體附近的微小區域,也就是進行局部搜索。
3 算法流程
算法的具體步驟如下:
Step1:設置進化代數,隨機產生M個初始個體組成初始種群 p(t),并求出各個個體的適應度 Fi(i=1,2,…,M)。
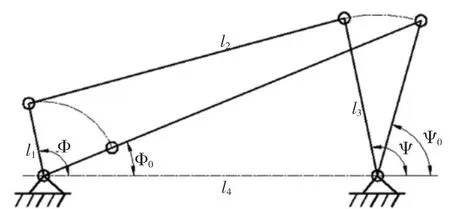
Step2:根據個體的適應度對其進行降序排列,記憶前N個個體(N Step3:選擇運算。用前面提的多輪輪盤賭法,對群體P(t)進行選擇運算,得到種群p'(t)。 Step4:交叉運算。對種群p'(t)進行算術交叉運算,得到種群p''(t)。 Step5:變異算法。對種群p''(t)進行非均勻變異運算,得到種群p'''(t)。 Step6:小生境排擠運算。將上面經過選擇、交叉、變異運算得到的M個個體和步驟2所記憶的N個個體合并在一起,得到一個含有M+N個個體的新群體。按照式(1)求出這M+N個個體中每兩個個體Xi和Xj之間的海明距離。當 Xi-Xj莨L時,比較個體Xi和Xj的適應度大小,并對其中適應度較低的個體處以罰函數。 Step7:敏度優化運算。按照式(5)計算得到的靈敏度向量,對這M+N個個體進行靈敏度優化。 Step8:計算、評價這M+N個個體,按適應度降序排序,并分別記錄記憶前M和前N個個體。 Step9:終止條件判斷。若不滿足終止條件,則:t=t+1,并將步驟8排序中的前M個個體作為新的下一代群體P(t),轉到步驟3;若滿足終止條件,則輸出計算結果,算法結束。 為了驗證本文提出的改進算法的性能,選用Shubert作為測試函數,這是一個多峰函數,該函數在其定義域內共有760個局部最小值,其中18個是全局最小值。全局最優點處的函數值為F=-186.73090883,其函數數學表達式如下: 本試驗用Matlab語編寫程序,種群規模M=100,記錄優秀個體為N=40,最大進化代數T=500,交叉概率pc=0.8,變異概率pm=0.1,海明距離下限L=0.4,罰函數Penalty=10-3,自適應交叉參數a0=40.0,靈敏度運算中參數η=10-4。 表1給出了本文算法與常規遺傳算法(GA)、基本小生境遺傳算法(NGA)、改進的小生境遺傳算法(GNGA)[8]的性能對比: 表1 本文算法與其他遺傳算法的性能對比 從表1中的結果可以明顯看出,本文所使用的改進算法對多峰Shubert函數進行全局尋優,收斂速度明顯比其他遺傳算法要快,計算結果的精確度也較高。 以文獻[9]中的曲柄搖桿機構再現運動規律為優化實例。所謂再現運動規律,是指當主動件運動規律一定時,要求從動件按給定規律運動[10],曲柄搖桿機構簡圖如下所示: 圖1 曲柄搖桿機構簡圖 由于按比例對桿件的長度進行縮放,將不會改變曲柄搖桿機構的運動規律,所以通常情況下設l1=1,l2、l3可由l1決定,機架長l4事先給定,因而設計變量定為: 其中l2、l3為桿件尺寸。 以給定的運動規律與機構實際運動規律間的偏差最小為目標函數,即: 其中ΨEi為期望輸出角,Ψi為實際輸出角,m為輸入角的等分數。 約束條件由傳動角滿足的許用值和曲柄搖桿機構滿足的曲柄存在條件決定,傳動角的最大最小許用值為,通過計算整理得約束為: 用基于靈敏度分析改進的遺傳算法,對曲柄搖桿機構再現運動規律進行優化,并與小生境GA[9]及罰函數法[10]的優化結果進行對比,如表2所示。 表2 本文算法與其他算法的計算結果對比 如表2所示,本文的算法收斂精度較高,而且結果更優。 本文將傳統優化算法的精髓導數信息引到了遺傳算法中,在保證了算法的全局搜索能力的同時,加強了算法的局部搜索能力。小生境技術的利用,增加了種群中個體的多樣性,在保留了最優解的同時,有效的防止了早熟現象的發生。改進的遺傳算子,改善了算法的各項性能,有效提高了算法的可靠性。通過對多峰Shubert函數的仿真試驗,說明該算法能有效的提高局部搜索能力及解的精度;對曲柄搖桿機構再現運動規律的實例優化,表明該算法具有一定實際應用價值。 [1]Holland J H.Adaptation in Natural and Artificial Systems[M].Cambridge,MA,USA:MIT Press,1975. [2]周洪偉,徐松林,徐 靜.改進的小生境遺傳算法[J].軟件時空,2007,23(6-3):208-209. [3]何新貴,梁久禎.利用目標函數梯度的遺傳算法[J].軟件學報,2001,12(7):981-986. [4]周 麗,孫樹棟.遺傳算法原理及應用[M].北京:國防工業出版社,2001. [5]HAFTKA R T.Second order sensitivity derivatives in structural optimization[J].AIAA Journal,1982,(20):1765-1766. [6]陳友文.一種改進選擇算子和基于小生境的遺傳算法[J].計算機與數字工程,2006,37(6):21-24. [7]董 穎,劉歡杰.一種基于實數編碼的改進遺傳算法[J].東北大學學報,2005,26(4):119-221. [8]黃聰明,陳湘秀.小生境遺傳算法的改進[J].北京理工大學學報,2004,24(8):675-678. [9]陳格娟,崔 煒,張京軍.小生境遺傳算法在機械優化設計中的應用[J].河北建筑科技學院學報,2004,21(1):56-59. [10]劉惟信.機械最優化設計[M].北京:清華大學出版社,1994.4 試驗及實例優化
4.1 試驗及分析


4.2 實例優化
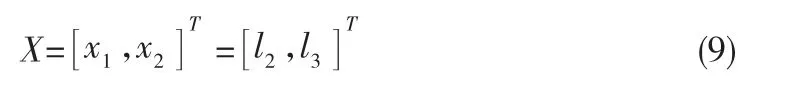




5 結束語

