圓中空夾層鋼管混凝土純扭構件工作機理研究

黃 宏,黃斌潔

（華東交通大學土木建筑學院,江西南昌 330013）

中空夾層鋼管混凝土是在兩個同心放置的鋼管中間填充混凝土而形成的新型組合結構,繼承了普通鋼管混凝土的承載力高、延性好、施工方便、經濟性好等優點,又由于特殊的截面形式而具有抗彎剛度大、自重輕、抗震性能和耐火性好等特點[1]。當中空夾層鋼管混凝土被用做構筑物獨立柱、輸電塔桿、發電風車支架時會受到扭矩作用,而國內外對這方面研究的報道尚屬空白,因此有必要對其抗扭性能進行研究。中空夾層鋼管混凝土的內、外鋼管可采用圓、方、矩形或其他截面形狀鋼管,由于圓形鋼管有利于防止局部屈曲,因此,本文擬對圖1所示截面形式的圓中空夾層鋼管混凝土構件進行研究,圖1中Do,Di,to和ti分別為外鋼管和內鋼管的外徑和厚度。

國內外已有研究者對實心鋼管混凝土純扭構件進行了試驗研究和數值模擬。Kitada和Nakai（1991）[2]進行了1個方鋼管混凝土短柱抗扭性能的試驗研究,同時也進行了空鋼管和素混凝土短柱純扭構件的對比實驗。韓林海和鐘善桐（1995）[3]進行了4個圓鋼管混凝土的純扭試驗研究。Beck和Kiyomiya（2003）[4]進行了圓鋼管混凝土、素混凝土和空鋼管柱純扭構件的對比實驗。堯國皇等（2007）[5]采

用有限元方法對鋼管混凝土純扭構件的荷載-變形關系進行計算,并進行了參數分析。陳宇超等（2009）[6]采用有限元軟件對矩形鋼管混凝土構件在純扭受力狀態下的力學性能進行了研究。

本文擬采用有限元方法對鋼管混凝土純扭構件的扭矩-轉角關系進行計算,并與其他研究者的試驗結果進行對比。在數值模擬結果得到試驗結果驗證的基礎上,對圓中空夾層鋼管混凝土純扭構件的扭矩-轉角全過程曲線進行計算。通過計算結果的全過程分析來研究圓中空夾層鋼管混凝土構件在扭矩作用下的工作機理。

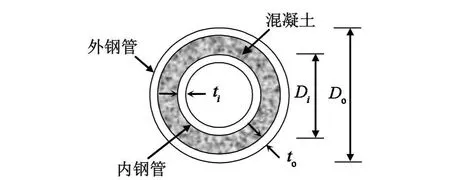
圖1 構件截面示意圖

1 有限元模型的建立

利用有限元軟件ABAQUS進行建模,對圓中空夾層鋼管混凝土純扭構件的扭矩-轉角全過程曲線進行計算。

1.1 單元類型和劃分

由于模擬中空夾層鋼管混凝土扭轉構件,單元網格會產生扭曲,應選用減縮積分單元。本文蓋板、內外鋼管和混凝土均采用8節點減縮積分格式的三維實體單元（C8D8R）。模型截面采用結構化網格劃分技術,在構件的長度方向上進行均勻的網格劃分。

1.2 材料的本構關系模型

鋼材的本構關系模型采用ABAQUS軟件中的彈塑性模型,該模型在多軸應力狀態下滿足經典的Von Mises屈服準則,采用各向同性的強化法則。本文低碳軟鋼采用五段式二次塑流模型來描述其塑性性能的應力-應變關系曲線[7]。鋼材彈性模量和泊松比分別取206 000 MPa和0.3。蓋板則考慮其為剛性材料,計算時彈性模量和泊松比分別為1×1012MPa和1×10-6。

混凝土的本構關系模型采用混凝土塑性損傷模型。該模型需要分別采用受拉和受壓的應力-塑性應變關系來定義材料的性能。對于單調荷載下的受拉混凝土,采用能量破壞準則來考慮混凝土的受拉軟化性能即應力-斷裂能關系[8]。單軸受壓應力-應變關系則采用劉威（2005）[9]改進的鋼管混凝土中核心混凝土模型,該模型考慮了核心混凝土受鋼管被動約束的特點,更適合有限元軟件ABAQUS對核心混凝土受壓應力-應變關系的分析。核心混凝土的泊松比 μc取0.2,彈性模量按Ec=4 730 fc（MPa）計算,其中fc為混凝土圓柱體抗壓強度。

1.3 鋼管與混凝土的界面模型

蓋板和內外鋼管均采用綁定（Tie）約束,以保證加載轉角位移時,蓋板和鋼管位移一致。蓋板和混凝土的界面模型采用法向硬接觸來模擬。內外鋼管與混凝土的界面模型由法向的接觸和切向的粘結滑移組成,在法向方向參考Beck和Kiyomiya（2003）[4]的研究方法,采用接觸剛度較大的單元來模擬,計算時接觸單元剛度為1 000 N?mm-1。在鋼管和混凝土的切向,采用庫侖摩擦模型來模擬鋼管與核心混凝土界面切向力的傳遞,摩擦系數μ取0.6。

1.4 邊界條件

采用全構件模型進行模擬計算,計算模型如圖2所示,模型一端為固定邊界,另一端約束其豎向位移。采用位移加載方法,在非固定邊蓋板的幾何中心設置參考點,在參考點處施加轉角位移,該參考點和蓋板上表面用Couple耦合。

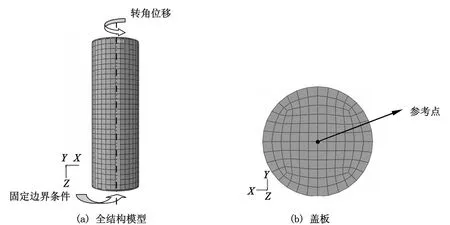
圖2 純扭構件計算模型

2 數值模擬結果與試驗結果對比

為了驗證上述數值模型的正確性,采用上述方法對圓鋼管混凝土純扭構件的扭矩-轉角關系進行了計算,并與文獻[3,10-12]的試驗結果進行對比。對比結果見表1,其中D為圓鋼管直徑,t為管壁厚度,fy為鋼材的屈服強度,fcu為混凝土立方體抗壓強度,Tue為試件抗扭強度試驗值,Tuc為試件抗扭強度計算值,其中抗扭強度 Tue和 Tuc為試件邊緣剪應變達10 000 μ ε時對應的極限扭矩Tu[3]。表1中,有限元計算的抗扭強度與試驗測得抗扭強度的比值（Tuc/Tue）的平均值為0.901,均方差為0.062。圖3為表1中部分圓鋼管混凝土純扭試件扭矩-轉角曲線計算結果與試驗結果的比較。由此可見,有限元計算結果與試驗結果吻合較好,且總體偏于安全。

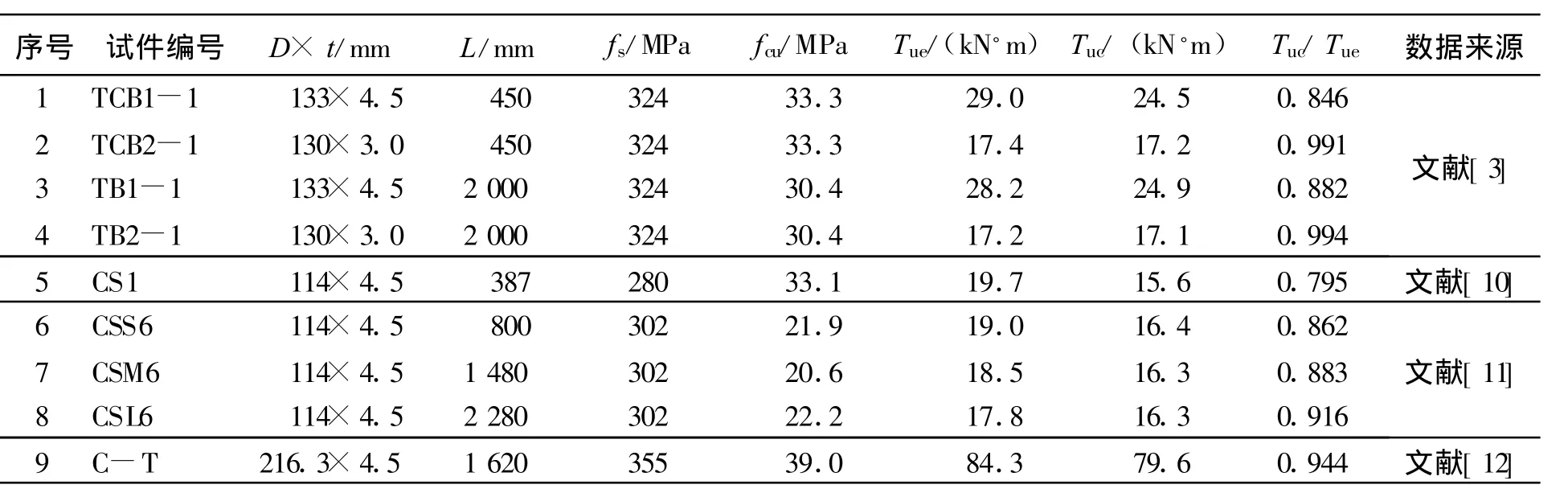
表1 純扭試件一覽表

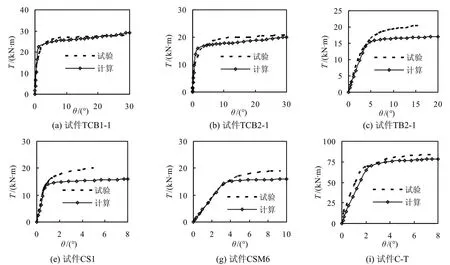
圖3 純扭扭矩-轉角曲線試驗結果與計算結果的比較

3 工作機理研究

本節采用以上有限元計算模型,通過典型算例對圓中空夾層鋼管混凝土純扭構件的工作機理進行研究,典型算例的基本條件是:Do=400 mm,to=9.31 mm,fyo=345 MPa,fyi=345 MPa,αn=0.1,χ=0.5,Di/ti=60,L=1 200 mm,其中 fyo為外鋼管的屈服強度,fyi為內鋼管屈服強度,αn為名義含鋼率（αn=Aso/Aco,Aso為外管截面積,Aco為外管以為所包圍的面條）,χ為空心率（χ=Di/（Do-2to））。典型算例的扭矩-轉角全過程曲線如圖4所示,圖中,T為扭矩,θ為構件總扭轉角。圖5和圖6給出了圓中空夾層鋼管混凝土典型算例中鋼管和混凝土截面 a點、b點和c點對應的固定邊界剪應力τxz分布。圓中空夾層鋼管混凝土純扭構件的典型T-θ曲線可分為下面幾個階段:

（1）彈性階段（oa）在此階段,T-θ關系曲線基本呈直線關系,內外鋼管和混凝土全部參加工作,三者一般是單獨受力,幾乎無相互作用力產生。在此階段,混凝土截面剪應力增長較快（如圖5（1）所示）。

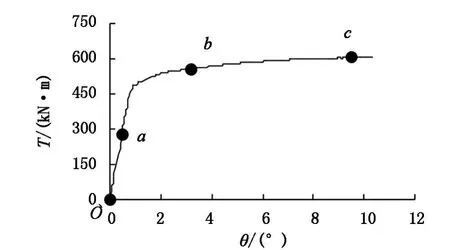
圖4 典型純扭構件 T-θ關系曲線

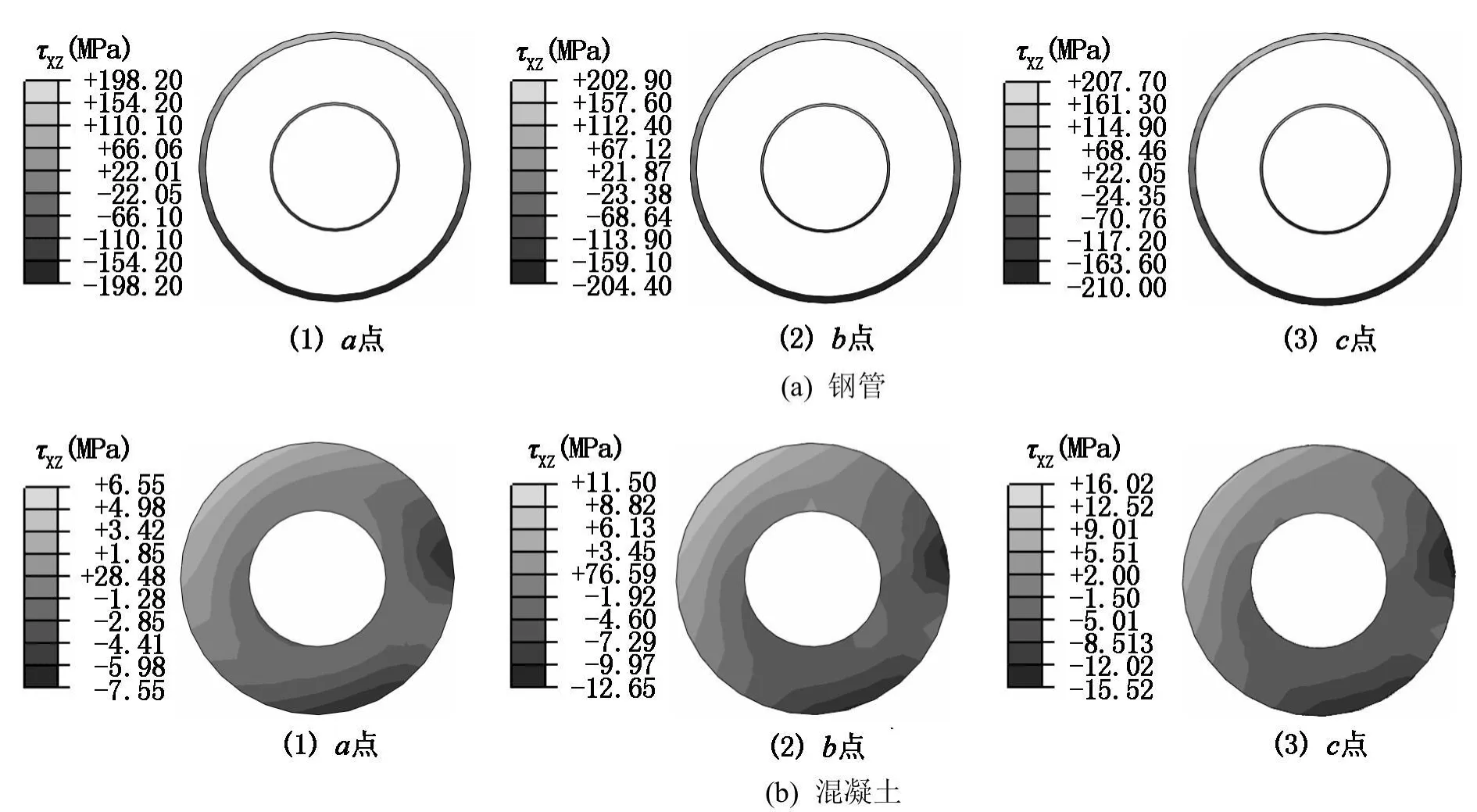
圖5 圓中空夾層鋼管混凝土純扭構件截面剪應力τxz分布云圖

（2）彈塑性階段（ab）達到a點時外鋼管進入彈塑性階段,內鋼管也隨后進入彈塑性階段。在扭矩作用下,內部混凝土開始發展微裂縫,由于微裂縫的擴展,使得混凝土的橫向變形超過了鋼管的橫向變形,這樣三者之間產生了相互作用力。由于與混凝土的相互作用,外鋼管先達到屈服,隨后內鋼管也達到屈服。鋼管和核心混凝土均處于復雜受力狀態之下,但主要處于雙向受剪的應力狀態。當構件進入彈塑性階段,混凝土截面剪應力增長幅度減小。

（3）塑性強化階段（bc）,當鋼管屈服后,雖然混凝土已發展了微裂縫,但由于受到外鋼管的約束,且由于混凝土的存在可以有效地抑制鋼管的局部內凹屈曲,從而使構件的抗扭承載力繼續增長,鋼管混凝土表現出良好的塑性性能。在此階段,混凝土界面剪應力增長幅度趨于平緩。對于圓中空夾層鋼管混凝土,在受力過程中,混凝土截面剪應力的分布始終是隨著與截面中心距離的增加,混凝土剪應力也增加（如圖6所示）。

圖7給出了圓中空夾層鋼管混凝土純扭構件典型算例在受力過程中內外鋼管與混凝土之間的相互作用力沿構件截面的分布。由圖可見,外鋼管主要以受壓為主,而內鋼管則受到拉力作用,這是因為內部混凝土在扭矩作用下發展裂縫使其橫向變形超過鋼管的橫向變形。圓中空夾層鋼管混凝土純扭構件內外鋼管的約束力在與構件成45°左右的截面處較大。圓中空夾層鋼管混凝土中的混凝土在扭矩的作用下的開裂為拉裂,其破壞面為45°左右翹曲面。但由于內外鋼管的約束作用,使混凝土裂縫的發展得到延緩并且阻止其發生錯位,因此沿軸線成45°左右翹曲面上產生比其他位置更大的相互作用力。

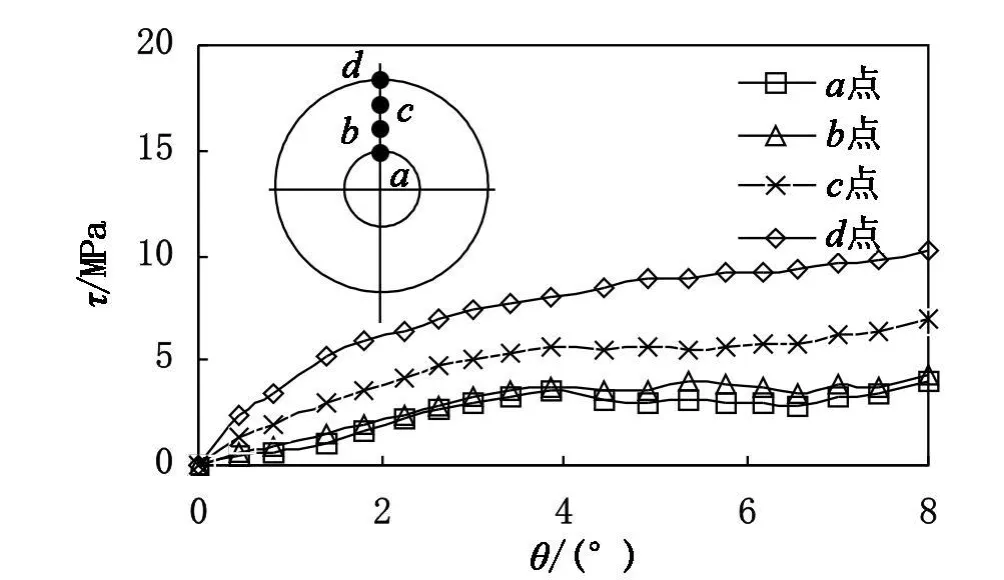
圖6 純扭構件混凝土不同位置處剪應力（τ-θ）關系曲線

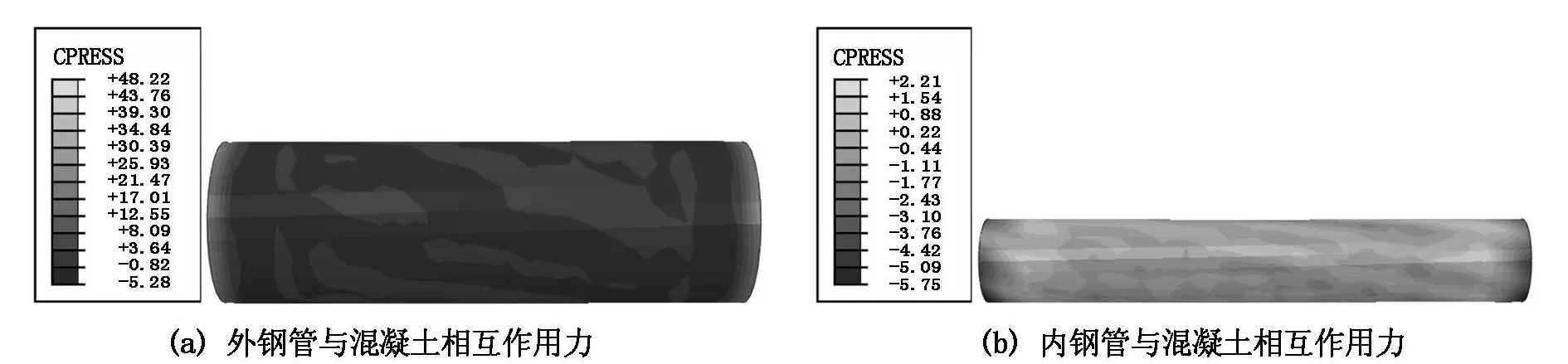
圖7 純扭構件內外鋼管與混凝土相互作用力分布（MPa）

4 結語

通過本文的分析可得如下結論:

（1）本文所建立的有限元模型能很好的模擬鋼管混凝土純扭構件,計算所得的構件抗扭承載力與試驗結果符合良好,并且計算結果總體趨于安全。

（2）在此基礎上,計算了圓中空夾層鋼管混凝土純扭構件典型算例的扭矩-轉角全曲線。全曲線分為三個階段:彈性段、彈塑性段和塑性強化段。全曲線不出現下降段,表明圓中空夾層鋼管混凝土純扭構件具有良好的塑性性能。

（3）通過分析三個階段中的內外鋼管和混凝土的剪應力分布以及他們之間的相互作用力,表明鋼管和混凝土在扭矩作用下能充分發揮各自的受力優勢,使得圓中空夾層鋼管混凝土具有優良的抗扭受力性能。

[1]黃宏,韓林海,陶忠.圓中空夾層鋼管混凝土柱軸壓工作機理研究[J].工業建筑,2006,36（11）:11-14.

[2]KITADA T,NAKAI H.Experimental study on ultimate strength of concrete-filled square steel shortmembers subjected to compressionor torsion[C]//Proceeding of the Inter.Confer.On Steel-concrete Composite Structures.Fukuoke,Japan,1991:137-142.

[3]韓林海.鋼管混凝土純扭轉問題研究[J].工業建筑,1995,25（1）:7-13.

[4]BECK J,KIYOMIYA O.Fundemental pure torsional properties of concrete filled circular steel tubes[J].Materials,Conc.Struct.Pavaments,JSCE,2003,60（739）:285-296.

[5]HAN LINHAI,YAO GUOHUANG,TAO ZHONG.Performance of concrete-filled thin-walled steel tubes under pure torsion[J].Thin-Walled Structures,2007,45（1）:24-36.

[6]陳宇超,張鵬鵬,王文達.矩形鋼管混凝土構件扭轉性能初探[C].中國鋼結構協會鋼—混凝土組合結構分會第十二次學術會議論文集,2009:13-16.

[7]韓林海.鋼管混凝土結構-理論與實踐[M].北京:科學出版社,2004.

[8]HILLER A,MODEER N W,MCHENRY P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement and Concrete Research,1976,6（6）:733-782.

[9]劉威.鋼管混凝土局部受壓時的工作機理研究[D].福州:福州大學,2005.

[10]宮安.鋼管混凝土短柱在壓扭復合受力下的研究[D].北京:北京建筑工程學院,1989.

[11]周競.鋼管混凝土中長柱在壓扭復合受力下的試驗研究[D].北京:北京建筑工程學院,1990.

[12]陳逸瑋.鋼管混凝土柱形狀因素于扭轉韌性行為研究[D].國立中央大學土木工程系,2003.