組學數據的核主成分聚類分析的可視化方法＊

哈爾濱醫科大學衛生統計學教研室 (150086) 孫 萌 張 濤 李 康

采用核主成分分析法(kernel p rincipal component anal

ysis,KPCA)。近幾年,核主成分分析法受到越來越多的重視,本文在簡要介紹 KPCA原理的基礎上,通過對模擬數據和實際數據的運算考核其可視化效果,并且對 PCA和 KPCA兩種方法進行了比較。

基本原理

核主成分分析法是將核函數與主成分分析法結合,通過事先確定的非線性映射函數φ,將輸入向量 Xk(k=1,2,…,m)映射到特征空間 H:φ(Xk)中,然后在該特征空間 H中對數據進行主成分分析〔1,2〕。通常情況下,我們并不了解變量間真正的關系,采用不當的非線性函數,反而使結果不理想,并可能引起維數災難。核函數則可以避免上述問題,它把非線性變換后的高維空間的內積運算轉換為原始空間中的核函數計算,不需要明確給出φ的具體形式,而是通過計算核函數K(Xi,Xj)的值來計算內積。核主成分分析方法不是基于變換后的特征空間的協方差矩陣來計算特征向量,而是先求出輸入向量的核矩陣,在此核矩陣的基礎上算得其特征向量和特征值,從而避免了直接在變換后的高維空間求特征向量的運算,大大減小了計算量。

KPCA法進行數據可視化分析的基本計算步驟簡述如下:

(1)選定核函數,并以此來計算輸入向量的核矩陣K;

(2)將 K矩陣中心化;

(3)按公式λiαi=Kαi計算矩陣 K的特征向量αi和特征值λi;

(4)為了確保原樣本的非線性相關系數矩陣的特征向量為單位向量,還需將相應的αi通過進行規范化;

針對具體數據,核函數的選擇是一個重要的問題,采用不同的核函數,可以構造原始變量不同類型的關系。任何一個函數只要滿足M ercer條件,就可以作為核函數,常用核函數有多項式核函數、徑向基核函數(RBF)、平方核函數和 Sigm oid核函數〔1,2〕。其中徑向基核函數 (RBF)被認為是一個較為穩健的核函數。計算軟件可以使用M atlab7.6.0核主成分分析工具包等程序。

模擬試驗

模擬試驗的目的是,在類間可分的情況下,考察核主成分聚類分析的可視化效果,并在相同條件下對PCA和 KPCA兩種方法的可視化效果進行比較。

1.模擬實驗 1

由圖 1(a)和圖 1(b)可見,當對分類有作用的差異變量間存在非線性關系時,KPCA的聚類可視化結果明顯優于 PCA的結果。KPCA的分析結果不僅能夠準確地反映兩組的分類情況,而且組間的樣品點相距較遠,而 PCA兩類的樣品卻混在一起無法分辨。

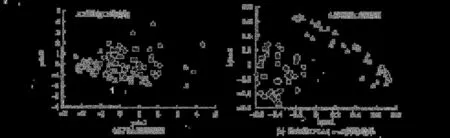
圖 1 PCA和徑向基 KPCA的兩種可視化方法比較

2.模擬實驗 2

在模擬實驗 1的基礎上,分別混入 m′=50,200,500,1000個與分類無關的正態變量作為干擾變量,PCA和 KPCA分析結果如圖 2。結果顯示,加入 50、200和 500個對分類不起作用的無差異變量時,KPCA仍具有顯著的分類可視化效果,但隨著無差異變量數目的增加 (如 m′=1000),其聚類效果會明顯變差。

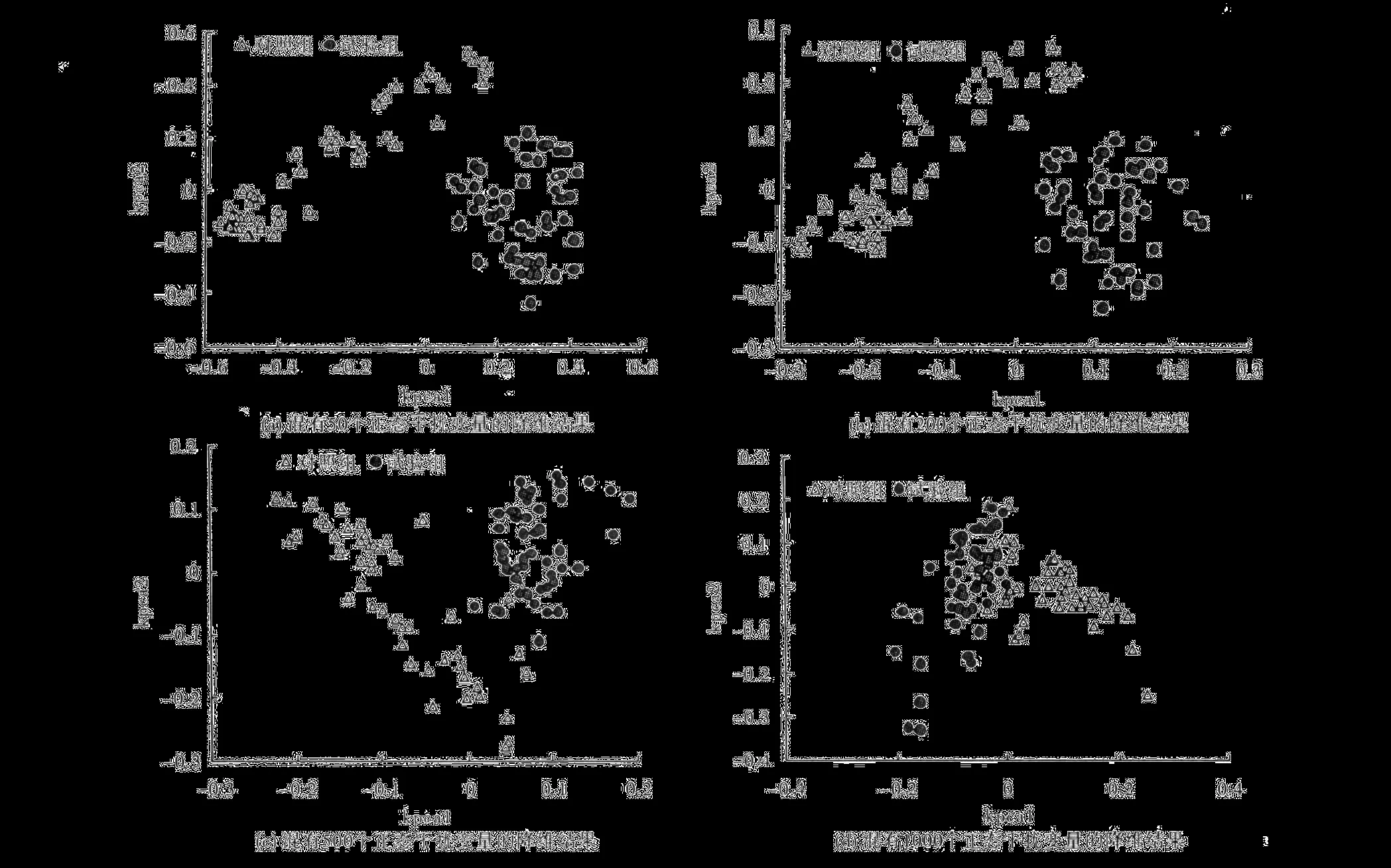
圖 2 加入不同數目正態干擾變量時徑向基 KPCA的可視化結果比較 (σ=8)

實 例

為進一步研究核主成分分析法對高維數據的可視化效果,現選取一個真實的實驗數據。實驗分為對照組、服用營養素兩組,每組各 10只小鼠,對其尿液的代謝組分用超高效液相色譜 -質譜聯用儀進行檢測,其中具有 886個代謝組分。在保持所有代謝組數據未進行變量篩選情況下,采用徑向基函數作為核主成分分析法的核函數,比較 KPCA與 PCA的效果,結果見圖3。結果顯示,PCA的分析結果不夠理想,但徑向基KPCA分析結果則較好地表示出了兩組的分類情況,說明其中可能含有具有生物學意義的代謝組成分。

小 結

與主成分分析法不同,核主成分分析法能夠解決變量間的非線性相關問題,其適用性更廣。用核主成分進行聚類分析時,需要設置的參數很少,改變這些參數可以得到更好的效果,本文用模擬試驗和實例說明了使用核主成分進行可視化分析的有效性。由于設定不同核函數的參數會產生不同的可視化效果,因此實際應用中需要確定最合適的核函數和參數。如果在作核主成分分析前,有針對性地對變量進行篩選,能夠獲得更好的可視化效果。

圖 3 營養代謝組實驗數據 PCA和 KPCA(RBF)的可視化結果比較

1.Sch?lkopf B,Burges C,Sm ola A.A dvances in kernel methods:support vector learning.Cam bridge:The M IT Press,1999.

2.Sch?lkopf B,Smola A,Müller KR.Nonlinear component analysis as a kernel eigenvalue p roblem.Neural Computation,1998,10(5):1299-1319.