多軸隨機(jī)振動(dòng)環(huán)境的疲勞損傷機(jī)理淺析

周興廣

（北京強(qiáng)度環(huán)境研究所，北京 100076）

0 前言

在振動(dòng)環(huán)境模擬試驗(yàn)領(lǐng)域，多軸振動(dòng)試驗(yàn)在產(chǎn)品故障模式復(fù)現(xiàn)和模擬精度方面具有顯著的優(yōu)勢(shì)，它能夠真實(shí)地模擬實(shí)際的動(dòng)力學(xué)環(huán)境，暴露產(chǎn)品在單軸激勵(lì)振動(dòng)方式下不易被發(fā)現(xiàn)的缺陷和隱患。一些已按規(guī)范通過單軸振動(dòng)的產(chǎn)品，在多軸振動(dòng)中會(huì)暴露出新的故障，而這些故障模式在實(shí)際使用過程中也會(huì)出現(xiàn)，從而表明多軸振動(dòng)環(huán)境試驗(yàn)可以更逼真地模擬使用環(huán)境[1-2]。

隨機(jī)振動(dòng)試驗(yàn)是考核產(chǎn)品結(jié)構(gòu)動(dòng)強(qiáng)度及環(huán)境適應(yīng)性的重要手段，是暴露結(jié)構(gòu)缺陷和鑒定設(shè)備承受使用環(huán)境能力的一種有效方法。通過對(duì)試驗(yàn)現(xiàn)場(chǎng)振動(dòng)測(cè)試數(shù)據(jù)的分析，發(fā)現(xiàn)產(chǎn)品在使用過程中的振動(dòng)環(huán)境絕大多數(shù)為多軸隨機(jī)環(huán)境，因此隨機(jī)載荷作用下結(jié)構(gòu)和部件的動(dòng)強(qiáng)度分析和疲勞壽命的預(yù)測(cè)尤為重要。據(jù)統(tǒng)計(jì)，工程構(gòu)件多是因承受隨機(jī)載荷作用而失效，疲勞損傷破壞約占到 80%以上。所謂疲勞損傷，是指產(chǎn)品及構(gòu)件在應(yīng)力或應(yīng)變的反復(fù)作用下所發(fā)生的性能變化。隨機(jī)載荷下疲勞損傷和可靠性的評(píng)價(jià)是一個(gè)關(guān)鍵的問題[3]。

1 多軸隨機(jī)振動(dòng)環(huán)境下的循環(huán)計(jì)數(shù)方法

多軸隨機(jī)振動(dòng)指的是同時(shí)使用多個(gè)振動(dòng)臺(tái)激勵(lì)一個(gè)試驗(yàn)件的高斯分布寬帶隨機(jī)振動(dòng)。文中主要針對(duì)高斯寬帶隨機(jī)振動(dòng)激勵(lì)的損傷機(jī)理進(jìn)行初步探討，分析多軸振動(dòng)損傷機(jī)理的計(jì)算方法及振動(dòng)特征與激發(fā)產(chǎn)品缺陷、加速產(chǎn)品失效的關(guān)系。

多軸振動(dòng)臺(tái)可分為兩類：一類是單方向激勵(lì)，即多個(gè)振動(dòng)臺(tái)平行激勵(lì)試件，當(dāng)各個(gè)振動(dòng)臺(tái)激勵(lì)相位相同時(shí)形成多臺(tái)同步振動(dòng)（圖1）；另一類是3個(gè)方向激勵(lì)，即振動(dòng)方向相互垂直，形成三軸相互垂直振動(dòng)（圖2），或者形成三軸向六自由度的空間運(yùn)動(dòng)（圖3）。試驗(yàn)數(shù)據(jù)表明：在多軸隨機(jī)振動(dòng)環(huán)境下，試件的應(yīng)力響應(yīng)與其受到的速度功率譜是等比例關(guān)系，速度功率譜可以通過試件上固定的加速度傳感器測(cè)得的時(shí)域信號(hào)轉(zhuǎn)化為加速度功率譜而計(jì)算得出。

圖 1 單方向多臺(tái)激振系統(tǒng)Fig. 1 One-way and multi-platform vibration system

圖 2 三軸振動(dòng)系統(tǒng)Fig. 2 Triaxial vibration system

圖 3 三軸向六自由度振動(dòng)系統(tǒng)Fig. 3 6-DoF triaxial vibration system

在隨機(jī)載荷作用下疲勞損傷機(jī)理的研究中，累積疲勞損傷分析方法在各種試件的載荷分析中都起著重要的作用。最早由Matsuishi和Endo[4]提出的主要以雨流計(jì)數(shù)法（Rainflow Counting）為核心的時(shí)域疲勞壽命估計(jì)方法應(yīng)用較為廣泛，并已成為標(biāo)準(zhǔn)的循環(huán)計(jì)數(shù)方法。雨流計(jì)數(shù)法對(duì)產(chǎn)品所承受的載荷時(shí)間歷程進(jìn)行循環(huán)計(jì)數(shù)，根據(jù)累積疲勞損傷理論計(jì)算出試件的疲勞循環(huán)壽命。經(jīng)典的雨流計(jì)數(shù)能夠處理單軸載荷的歷程，對(duì)多軸載荷的處理僅限于比例載荷。此后，Wang和Brown提出多軸疲勞計(jì)數(shù)法作為新的損傷計(jì)算方法，該方法采用傳統(tǒng)的相對(duì)當(dāng)量應(yīng)變法，其中循環(huán)被定義為從零到最大值的增加[5]。

Brown等指出了傳統(tǒng)的雨流計(jì)數(shù)方法的局限性，提出多軸非比例雨流計(jì)數(shù)方法和疲勞損傷計(jì)算流程[6]。Socie對(duì)多軸非比例隨機(jī)載荷中的4個(gè)問題，即循環(huán)應(yīng)力應(yīng)變模型、循環(huán)計(jì)數(shù)方法、損傷模型和損傷累積模型進(jìn)行了分析。指出Bannantine-Socie方法及Wang-Brown方法可應(yīng)用于比例載荷，但用于定義具有平均應(yīng)力的循環(huán)中仍有困難。

Anthes對(duì)經(jīng)典的雨流計(jì)數(shù)方法進(jìn)行了修正，對(duì)于應(yīng)力-應(yīng)變路徑的不封閉部分采用了虛擬滯環(huán)的概念，能夠考慮載荷順序的影響。Langlais等[7]通過對(duì)單軸循環(huán)計(jì)數(shù)方法簡(jiǎn)單修正后提出了多軸循環(huán)計(jì)數(shù)方法。在單軸情況下，應(yīng)力和應(yīng)變是同相的，應(yīng)變中的一個(gè)往復(fù)與應(yīng)力中的一個(gè)往復(fù)相一致。而多軸情況下應(yīng)力和應(yīng)變過程并不同相，如果仍對(duì)數(shù)據(jù)進(jìn)行計(jì)數(shù)，將難以保證不同的數(shù)據(jù)組間的關(guān)系。為了保證重要信息不被略去，必須考慮其他輔助通道的數(shù)據(jù)關(guān)系，從而實(shí)現(xiàn)多軸循環(huán)的計(jì)數(shù)。

Dirlik等提出了一個(gè)寬帶隨機(jī)應(yīng)力作用下疲勞壽命估計(jì)的經(jīng)驗(yàn)閉合解，即Dirlik經(jīng)驗(yàn)公式，以計(jì)算平穩(wěn)高斯應(yīng)力造成的疲勞損傷[8]。公式針對(duì)平穩(wěn)的、各態(tài)歷經(jīng)的高斯過程，從功率譜密度估計(jì)雨流計(jì)數(shù)法，利用波峰和波谷的近似模型，給出了一種多軸隨機(jī)振動(dòng)環(huán)境下的循環(huán)計(jì)數(shù)方法，該方法成為目前應(yīng)用最廣泛的隨機(jī)應(yīng)力疲勞壽命估計(jì)方法。

2 多軸振動(dòng)疲勞損傷分析方法

多軸疲勞是指疲勞損傷發(fā)生在多軸循環(huán)加載條件下，至少有兩個(gè)方向施加的應(yīng)力獨(dú)立隨時(shí)間變化。其變化可以是同相位、比例的，也可以是非同相位、非比例的。

多軸隨機(jī)載荷下的損傷累積研究并不多見。Fash等[9]針對(duì)多軸變幅載荷下的構(gòu)件進(jìn)行了分析，通過計(jì)算得到確切的峰值和谷值，采用傳統(tǒng)的局部應(yīng)變壽命的概念進(jìn)行疲勞壽命預(yù)測(cè)。

相對(duì)于單軸疲勞而言，多軸疲勞無論在力學(xué)、試驗(yàn)研究乃至物理機(jī)制方面都更為復(fù)雜。因?yàn)殡S著3個(gè)主應(yīng)力相對(duì)比值的改變，損傷可以在不同方向、不同平面內(nèi)形成。此外，在多軸情況下的循環(huán)應(yīng)力應(yīng)變特性，損傷的取向、形狀、擴(kuò)展方向、速率以及疲勞壽命等均受到更多因素的影響。由于多軸疲勞損傷機(jī)理和失效過程的理論分析與試驗(yàn)研究都還不足，尚有許多基本問題沒有解決，所以還沒有形成統(tǒng)一的理論[10]。

現(xiàn)有的多軸疲勞損傷分析方法主要有以下3種[11]。

1）等效應(yīng)力-應(yīng)變法：基于一定的靜強(qiáng)度理論，利用Von Mises最小畸變能原則或Tresca屈服準(zhǔn)則等，對(duì)多軸應(yīng)力狀態(tài)下的應(yīng)力（應(yīng)變）進(jìn)行等效。將等效應(yīng)力（應(yīng)變）作為損傷參量，估算出多軸狀態(tài)下構(gòu)件的壽命。等效應(yīng)力-應(yīng)變法不涉及到具體的多軸疲勞破壞機(jī)理。

2）能量法：基于能量建立疲勞損傷度，主要考慮多軸和平均應(yīng)力對(duì)材料變形的影響。能量法認(rèn)為塑性功的累積是產(chǎn)生材料不可逆損傷進(jìn)而導(dǎo)致疲勞破壞的主要原因，而材料達(dá)到疲勞斷裂時(shí)所需要的能量與加載方式無關(guān)。能量法可以應(yīng)用于多軸載荷條件下比例及非比例加載的壽命估算，但是能量法本身是標(biāo)量，不能反映出多軸疲勞破壞面，在估算長(zhǎng)壽命時(shí)誤差較大。

3）臨界損傷平面法：它不僅考慮應(yīng)力、應(yīng)變的大小，而且還考慮到它們所在的平面及方向，以建立一種與最大損傷平面上的應(yīng)變參數(shù)有關(guān)的疲勞

損傷參量。利用臨界平面理論，可以對(duì)比例及非比例兩種加載情形進(jìn)行壽命估算研究。該法反映了多軸疲勞變化破壞面具有一定的物理意義。但目前各種臨界損傷平面法基本上是基于試驗(yàn)的經(jīng)驗(yàn)公式，應(yīng)用范圍窄，且包含一些物理意義不明確的常數(shù)。

等效應(yīng)力-應(yīng)變法雖然不能反映材料內(nèi)部機(jī)理，但是它有效利用了單軸疲勞中成熟的理論和經(jīng)驗(yàn)數(shù)據(jù)，使用和計(jì)算方便，同時(shí)也能夠給出疲勞損傷的一個(gè)初步估計(jì)，所以實(shí)際工程中仍在廣泛應(yīng)用。目前，多軸疲勞頻域分析方法就是以等效應(yīng)力-應(yīng)變法為基礎(chǔ)，在頻域內(nèi)利用隨機(jī)應(yīng)力的統(tǒng)計(jì)參數(shù)來分析疲勞損傷的。

3 多軸正態(tài)隨機(jī)振動(dòng)的疲勞損傷計(jì)算

正態(tài)隨機(jī)是目前較為廣泛使用且很重要的應(yīng)力分布方式，很多統(tǒng)計(jì)方法都是由此分布引出的。多種類型的產(chǎn)品在涉及疲勞損傷問題時(shí)都可應(yīng)用正態(tài)隨機(jī)分布。

疲勞損傷分析方法的基本思路是從隨機(jī)應(yīng)力的統(tǒng)計(jì)特性功率譜估計(jì)出峰值應(yīng)力在單位時(shí)間內(nèi)的期望循環(huán)次數(shù)的概率密度函數(shù)，根據(jù)Miner準(zhǔn)則計(jì)算出期望疲勞損傷，最后得到疲勞損傷和疲勞壽命的估計(jì)。

正態(tài)分布的概率密度函數(shù)可表示為

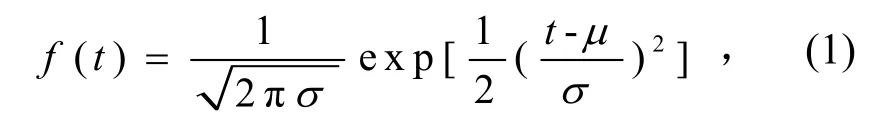
其中：-∞＜t＜+∞；-∞＜μ＜+∞；σ＞0 ；

正態(tài)分布的累積分布函數(shù)可表示為

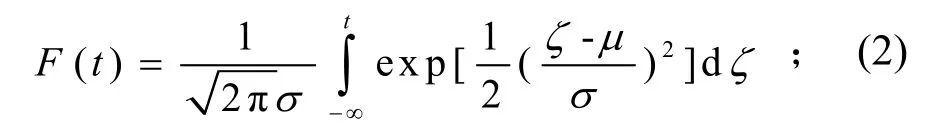
此分布關(guān)于其均值μ對(duì)稱，標(biāo)準(zhǔn)差σ表示離散度。對(duì)變量進(jìn)行簡(jiǎn)單變換，則(2)式得累積分布函數(shù)變?yōu)?/p>

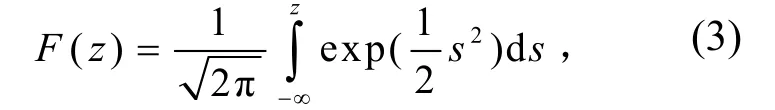
由應(yīng)力y1與它的一階導(dǎo)數(shù) y2和二階導(dǎo)數(shù)y3的聯(lián)合峰值概率密度函數(shù) f (y1y2y3)計(jì)算出單位時(shí)間內(nèi)應(yīng)力峰值的期望循環(huán)次數(shù)：

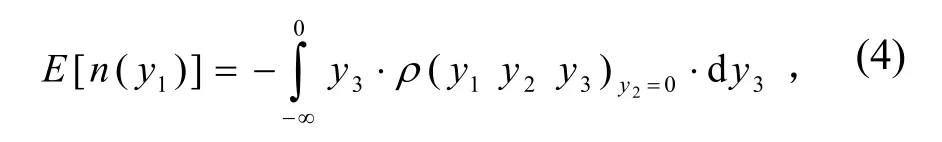
根據(jù) E [n(y1)] 估計(jì)其概率密度函數(shù)為

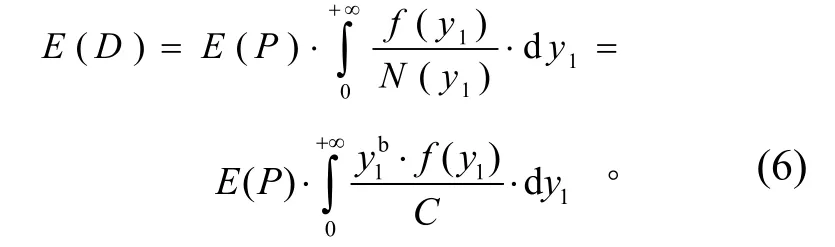
應(yīng)力在作用時(shí)間 T 后引起的期望疲勞損傷

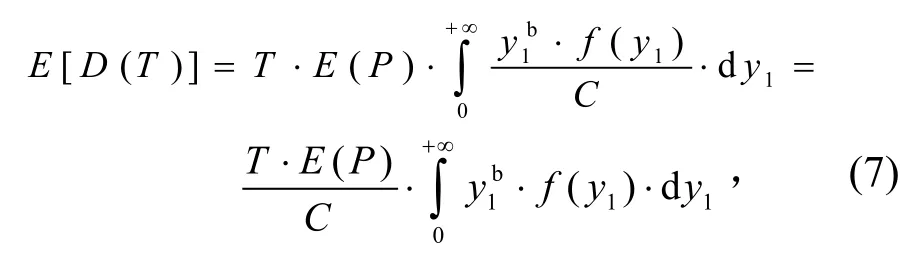
當(dāng) E [D(T)] = 1時(shí)，則試件已發(fā)生疲勞損壞，此時(shí)試件的總共作用時(shí)間TF，即期望壽命：

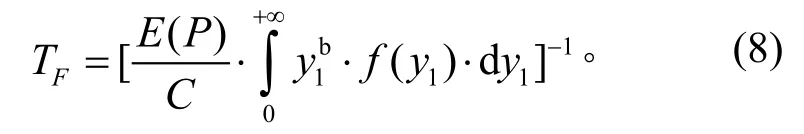
在疲勞損傷頻域分析方法中，應(yīng)力峰值期望循環(huán)次數(shù)E [n(y1)]的估計(jì)在處理隨機(jī)應(yīng)力疲勞問題的能力上起關(guān)鍵作用。

4 結(jié)束語

近年來，多軸隨機(jī)載荷下疲勞壽命的預(yù)測(cè)日益引起人們的重視，但因?yàn)閱栴}本身的復(fù)雜性使得對(duì)該研究仍處于數(shù)據(jù)累積階段，大量的試驗(yàn)研究有待進(jìn)一步深入。

振動(dòng)循環(huán)計(jì)數(shù)是隨機(jī)載荷下疲勞損傷計(jì)算的基礎(chǔ)。雨流計(jì)數(shù)方法幾經(jīng)修正完善，能夠?qū)崿F(xiàn)對(duì)多軸載荷下循環(huán)的計(jì)數(shù)。Dirlik經(jīng)驗(yàn)公式從功率譜密度估計(jì)雨流計(jì)數(shù)法，具有一定的物理背景，因此愈來愈受到各國(guó)學(xué)者的重視，結(jié)合多軸疲勞損傷分析的能量法以及Miner的線性損傷規(guī)律是目前多軸隨機(jī)振動(dòng)載荷疲勞損傷分析中常用的方法。

（

）

[1] 陳穎, 朱長(zhǎng)春, 李春枝, 等. 某結(jié)構(gòu)的多軸隨機(jī)振動(dòng)實(shí)驗(yàn)研究[J]. 實(shí)驗(yàn)力學(xué), 200924(1): 35-41

[2] 樊世超, 馮咬齊. 多維動(dòng)力學(xué)環(huán)境模擬試驗(yàn)技術(shù)研究[J].航天器環(huán)境工程, 2006, 23(1): 23-28

[3] 高樺. 多軸疲勞研究[J]. 機(jī)械強(qiáng)度, 1996, 18(1): 9-13

[4] Pitoiset X, Preumont A. Tools for a multiaxial fatigue analysis of structures submitted to random vibrations[J]. Journal of Vibration and Acoustics, 1994, 45(3)

[5] Spottswood S M, Wolfe H F. Comparing fatigue life estimates using experimental and spectral density based probability distributions[R]. American Institute of Aeronautics and Astronautics, 2001, 22(5): 155-162

[6] Adam Nies?ony. Comparison of some selected multiaxial fatigue failure criteria dedicated for spectral method[J]. Journal of Theoretical and Applied Mechanics, 2010, 48(1): 233-254

[7] Langlais T E, Vogel J H, Chase T R. Multiaxialcycle counting for critical plane methods[J]. International Journal of Fatigue, 2003, 64(5): 51-64

[8] Chen X, Jin D, Kim K S. Fatigue life prediction of 304 stainless steel under sequential biaxial load[J]. Int Fatigue, 2006, 28(3): 176-187.

[9] Bishop N W M, Sherratt F. A theoretical solution for the estimation of rainflow ranges from power spectral density data[J]. Fatigue Fract Engng Mater Stuct, 1990, 13(4)

[10] 金丹, 陳旭. 多軸隨機(jī)載荷下的疲勞壽命估算方法[J].力學(xué)進(jìn)展, 2006, 36(1): 65-74

[11] 尚德廣. 多軸疲勞損傷與壽命預(yù)測(cè)研究[D]. 西南交通大學(xué)博士學(xué)位論文, 1995