用類比法來探究圖像中“面積”的應用

李維兵

(南通高等師范學校 江蘇南通 226100)

類比法是中學物理教學中常用的一種基本方法,它是根據兩個對象在某些屬性或關系上相似而推出它們在另一個屬性或關系上也可能相似的一種推理形式.在教學中,類比法不僅體現在概念、原理的理解上,而且也體現在解題應用上.下面就用類比法來探究圖像中“面積”的應用.

【例1】總質量為80 kg的跳傘運動員從離地500 m的直升機上跳下,經過2 s拉開繩索開啟降落傘,圖1所示是跳傘過程中的v-t圖像,試根據圖像估算14 s內運動員下落的高度(g取10m/s2).

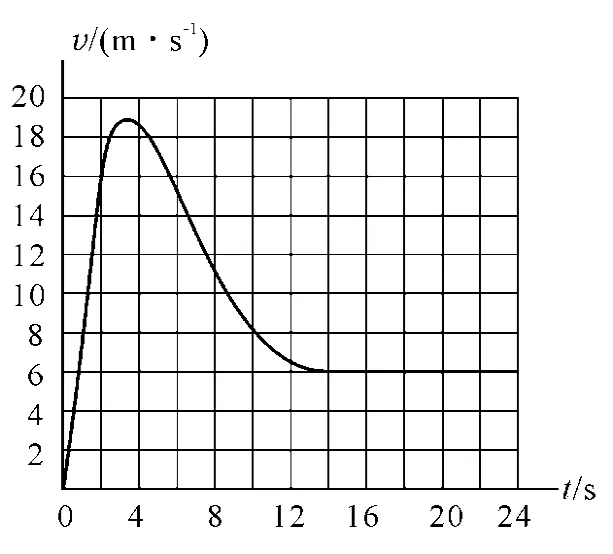
圖1

解析:由v-t圖中可知,運動員在14 s內速度是非線性變化,只能通過由面積估算得出運動員在14 s內下落的高度:即每格2×2m=4m,共計40×4m=160m(圖2).

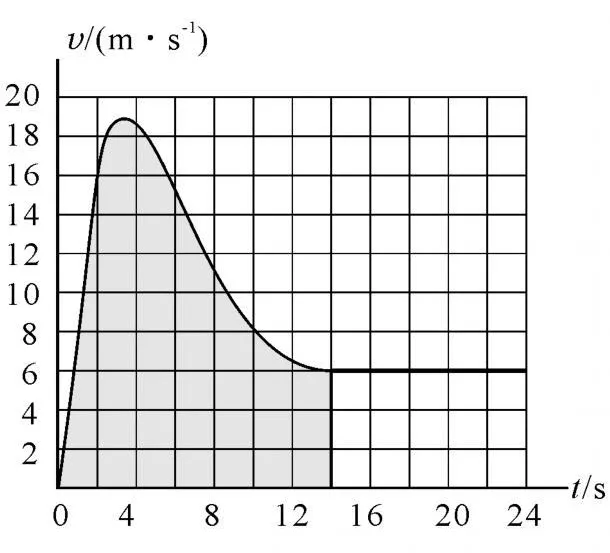
圖2

通過該題,我們知道了在v-t圖像中,速度曲線與t軸所夾的面積表示位移大小.

其實圖像中的“面積”應用很廣泛,在動力學、電學、熱學中都可涉及;下面分別從這三方面來探究.

1 圖像中的“面積”在動力學中應用

【例2】質量為2 kg的物體靜止在光滑水平面上,現對物體施加一水平力F,物體在力F作用下,產生的加速度a隨時間t的變化關系如圖3所示.重力加速度g取10m/s2,試根據圖3,求:

(1)物體開始運動時的拉力大小;

(2)估算物體在5 s內的平均加速度;

(3)估算拉力F在10 s內對物體所做的功.

圖3

解析:(1)由牛頓第二定律得

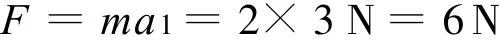
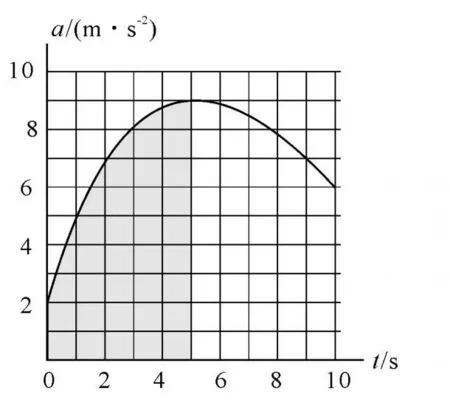
圖4

(2)與例1同理,由圖4估算可得5 s內的面積為35×1m/s2×1 s=35m/s,此時5 s內速度增量

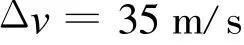
平均加速度

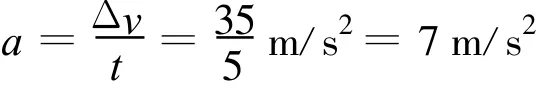
代入數據得

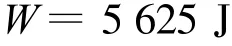
從a-t圖中,我們可以發現加速度隨時間的變化是非線性的.雖然沒有學過非線性變化下的平均加速度的求法,但是可以利用類比法,在a-t圖中加速度a隨時間的變化圖像與t軸所圍的面積表示速度的增量,即5 s內的面積可以表示5 s末的速度.這為動力學中解決變加速運動提供了一個求解的方法.

2 圖像中的“面積”在電學中應用

【例3】如圖5(a)所示,一邊長 L=2.5m、質量m=0.5 kg的正方形金屬線框,放在光滑絕緣的水平面上,整個裝置放在方向豎直向上、磁感應強度為B=0.8 T的勻強磁場中,它的一邊與磁場的邊界MN重合.在水平力F作用下由靜止開始向左運動,經過5 s,線框被拉出磁場.測得金屬線框中的電流隨時間變化的圖像如圖5(b)所示.在金屬線框被拉出的過程中:

(3)由圖像知v10=75m/s

(4)由動能定理得外力做功

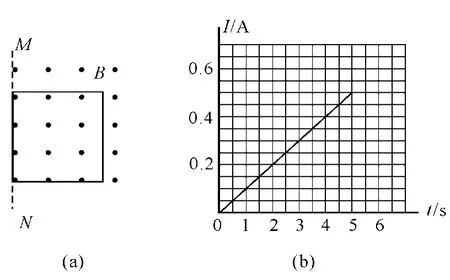
圖5

(1)求通過線框導線截面的電荷及線框的電阻;

(2)寫出水平力F隨時間變化的表達式;

(3)已知在這5 s內力F做功1.92 J,那么在此過程中,線框產生的焦耳熱是多少?

得

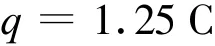
方法二 由I-t圖像中電流與時間所圍面積(圖6)得

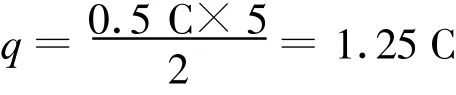
又根據

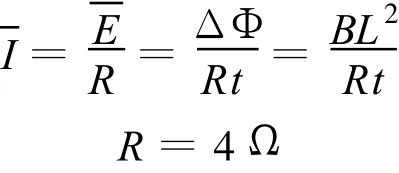
得

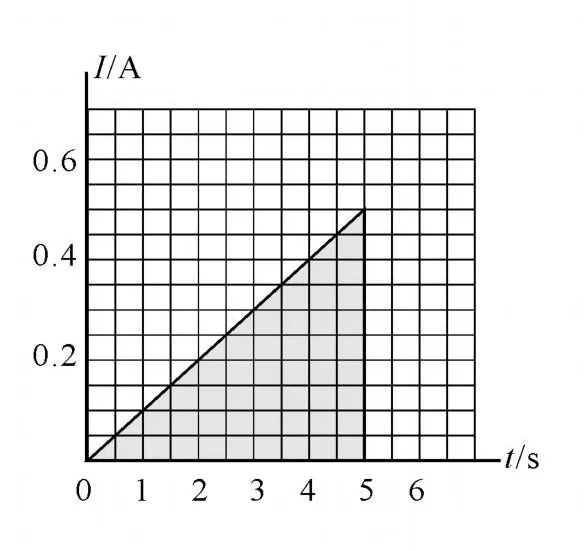
圖6

(2)由電流-時間圖像可知,感應電流隨時間變化的規律

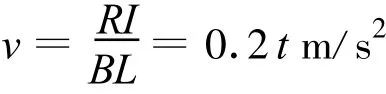
線框做勻加速直線運動,加速度

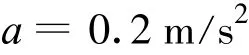
線框在外力F和安培力FA作用下做勻加速直線運動

(3)t=5 s時,線框從磁場中拉出時的速度

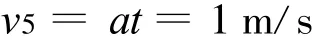
線框中產生的焦耳熱

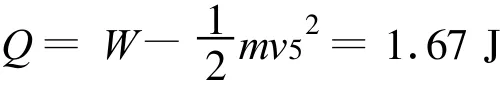
在線性變化下,平均值法和面積法都適用.在非線性變化下怎么辦?I-t圖線如圖7(a)所示,該如何求5 s內通過線框導線截面的電荷?

解析:如圖7(b),只能用面積法.

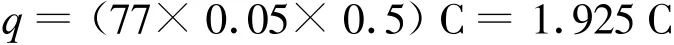
通過本題探究,我們發現在I-t圖中電流隨時間的變化圖像與 t軸所圍的面積表示電荷的增加.這在電學中解決電學量非線性變化時提供了一個求解的方法.

3 圖像中的“面積”在熱學中應用

【例4】圖8所示為一定質量的某種理想氣體由狀態A經過狀態C變到狀態B的圖像,下列說法正確的是

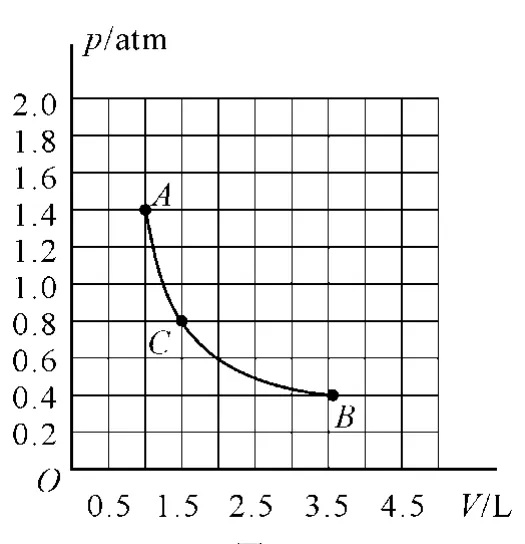
圖8

A.該氣體在狀態A時的內能等于在狀態B時的內能

B.該氣體在狀態A時的內能等于在狀態C時的內能

C.該氣體由狀態A至狀態B為吸熱過程

D.該氣體由狀態A至狀態C對外界所做的功大于從狀態C至狀態B對外界所做的功

解析:在A點pAVA的數值為1.4.在B點pBVB的數值為1.4.由恒量,故

理想氣體內能僅為溫度的函數,所以選擇A選項,排除B選項.從A態到B態,氣體一直對外做功,由ΔU=W+Q,可知,自A態至B態為吸熱過程,故選項C對.對于D選項,可以用面積來表示對外做功的多少.從A態到C態面積約占5格[圖9(a)];從C態到B態面積約占10格[圖9(b)]).不難看出從A態到C態對外做功比從C態到B態做功少,故選項D錯.

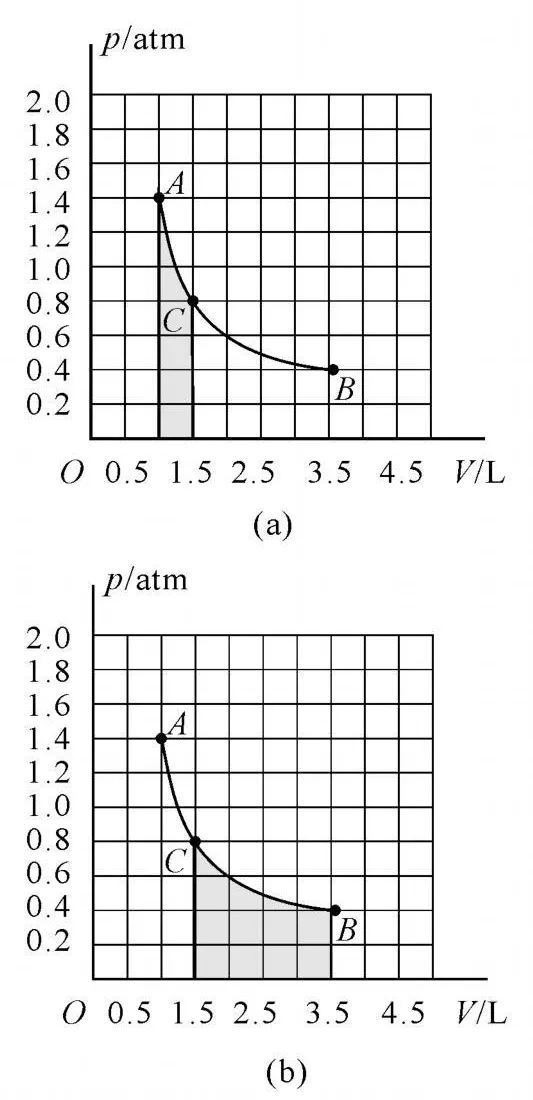
圖9

通過本題的探究,我們發現在p-V圖中壓強隨體積的變化圖線與體積所圍的面積表示對外做功的多少,這在熱學中解決壓強非線性變化下物體對外做功提供了一個求解的方法.

綜上所述,圖像中的“面積”在動力學、電學、熱學中均有應用,尤其對題目中涉及某個物理量隨另一個物理量非線性變化時,可以采用類比的思想使物體的復雜過程變得簡單明了.這種思維方法在物理解題過程中是非常重要的.