卵形鯧鲹貯藏過程中品質變化動力學模型

黃 卉，李來好*，楊賢慶，郝淑賢，馬海霞，岑劍偉，李 莎

(中國水產科學研究院南海水產研究所，廣東 廣州 510300)

卵形鯧鲹貯藏過程中品質變化動力學模型

黃 卉，李來好*，楊賢慶，郝淑賢，馬海霞，岑劍偉，李 莎

(中國水產科學研究院南海水產研究所，廣東 廣州 510300)

研究不同溫度貯藏條件下卵形鯧鲹揮發性鹽基氮值(TVB-N)、硫代巴比妥酸值(TBA)和菌落總數隨時間的變化規律及其動力學特性，建立TVB-N、TBA和菌落總數與貯藏溫度和貯藏時間的動力學模型，以預測和控制卵形鯧鲹在貯藏過程中的品質和貨架期。貯藏過程中卵形鯧鲹的TVB-N、TBA和菌落總數增加，隨著貯藏溫度的升高，卵形鯧鲹品質劣化速度加快。TVB-N、TBA和菌落總數均符合一級化學反應動力學模型，并且與Arrhenius方程有很高的擬合度。利用化學動力學原理建立了卵形鯧鲹貯藏過程中TVB-N、TBA和菌落總數的動力學模型：t= (lnAt－lnA0)/(1.68×109×e-56600/RT)，t= (lnAt－lnA0)/(3.10×108×e-52090/RT)，t= (lnAt－lnA0)/(1.87×108×e-47550/RT)。卵形鯧鲹的貯藏期可通過以上動力學模型進行預測。

卵形鯧鲹；揮發性鹽基氮(TVB-N)；硫代巴比妥酸值(TBA)；菌落總數；動力學模型

卵形鯧鲹俗稱金鯧、黃臘鯧，其肉色潔白細嫩，蛋白質、脂肪含量高，鮮美可口，是名貴食用海水魚。近年來，卵形鯧鲹的人工養殖取得了可喜進展，在廣東、廣西、福建均已進入網箱養殖[1]。卵形鯧鲹除了以活魚銷售外，大部分是以冰鮮魚和冷凍魚的形式銷售和出口，這兩種產品形式的卵形鯧鲹在貯藏過程中會發生品質變化。因此，監測和控制其品質變化是十分重要的，如何準確的預測卵形鯧鲹的貯藏期及合理確定其貯藏溫度是一個亟待解決的問題。

近年來，一些國內外學者利用化學動力學模型對冷藏魚[2-4]、冷卻肉[5-6]、板鴨[7]等的品質變化進行研究，并且預測其貨架期，而對卵形鯧鲹在貯藏過程中品質變化的動力學模型研究尚未見報道。本實驗主要針對卵形鯧鲹在貯藏過程中的揮發性鹽基氮(TVB-N)、硫代巴比妥酸值(TBA)和菌落總數進行測定，建立其隨貯藏溫度和時間變化的動力學模型，為貯藏過程中品質變化的預測提供參考。

1 材料與方法

1.1 材料與試劑

卵形鯧鲹：購于廣州市黃沙水產市場。將卵形鯧鲹體表洗凈，裝入袋中，真空包裝，分別貯藏于5、0、－10℃條件下，定期取樣，測定TVB-N、TBA及菌落總數，每個貯藏條件下的樣品平行測定3次。

高氯酸、鹽酸、硼酸、乙醇、三氯乙酸、氫氧化鈉、甲基紅、甲基藍等(分析純) 廣州化學試劑廠；硫代巴比妥酸(分析純) 上海遠帆助劑廠；營養瓊脂培養基 廣東環凱微生物制劑有限公司。

1.2 儀器與設備

紫外-可見分光光度計 上海精密科學儀器有限公司；蛋白質分析儀 丹麥福斯公司。

1.3 方法

1.3.1 TVB-N含量的測定

按照SC/T 3032—2007《水產品中揮發性鹽基氮的測定》方法測定。

1.3.2 TBA值的測定

取10g樣品研細，加入50mL 體積分數7.5% 三氯乙酸(含有1mg/mL EDTA)，振搖30min，雙層濾紙過濾兩次。取5mL上清液，加入5mL 0.02mol/L TBA溶液，沸水浴中保存40min，取出冷卻1h，5500r/min離心25min，取上清液，加入5mL氯仿搖勻，靜置分層后取上清液分別在532nm和600nm處比色，記錄消光值并用以下公式計算TBA值。

TBA/(mg/100g)=(A532－A600)/155×(1/10) ×72.6×100

1.3.3 菌落總數的測定

按照GB/T 4789.2—2003《食品衛生微生物學檢驗：菌落總數測定》的方法測定。

1.3.4 數據統計

采用Excel軟件和SAS軟件進行數據處理。

2 結果與分析

2.1 反應級數(n)的確定

食品品質在貯藏過程中的變化可用化學反應動力學來描述[8-9]。化學反應動力學的基本公式可表示為：

式中：A為品質因子的濃度；t為貯藏時間；K為變化速率常數；n為反應級數。

大多數食品的質量與時間關系表現出零級或一級的反應，即n=0或n=1，動力學方程如下：

圖1～3是卵形鯧鲹在不同溫度貯藏過程中TVB-N、 TBA和菌落總數與貯藏時間的關系。由3個圖可以看出，3個溫度下TVB-N、TBA和菌落總數與時間t近似呈指數關系，相關系數均大于0.9，根據(3)式可得卵形鯧鲹在貯藏中TVB-N、TBA和菌落總數的變化為一級反應，即反應級數n=1。

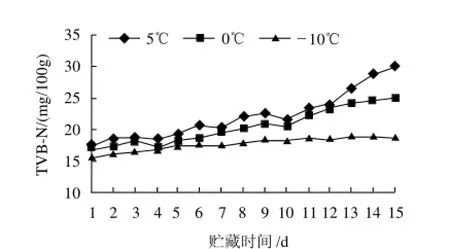
圖1 TVB-N與貯藏時間的關系Fig.1 Relationship between TVB-N and storage time

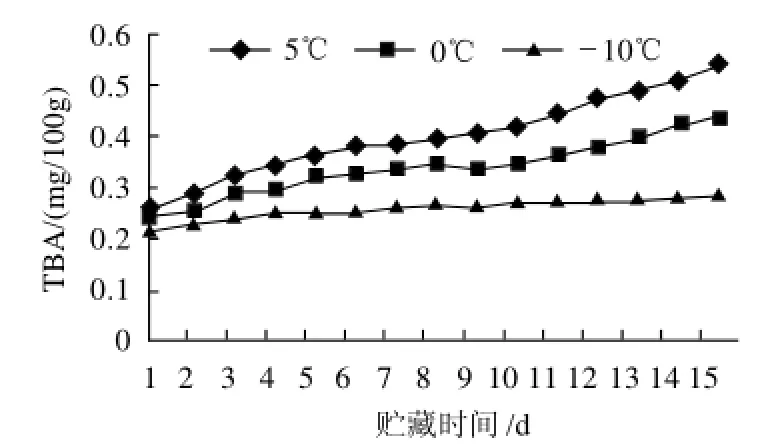
圖2 TBA與貯藏時間的關系Fig.2 Relationship between TBA and storage time

圖3 菌落總數與貯藏時間的關系Fig.3 Relationship between total bacterial count and storage time

2.2 反應速率常數K的確定

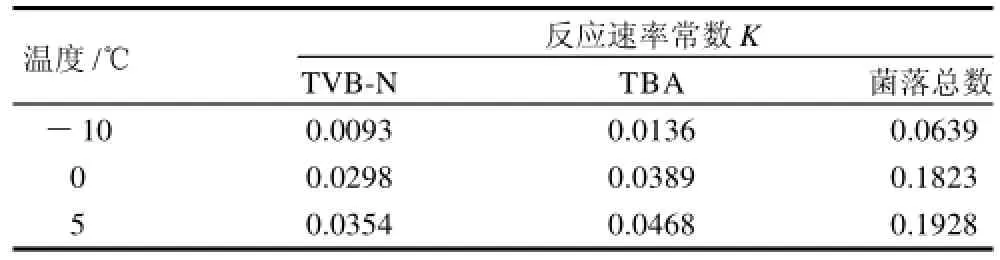
表1 TVB-N、TBA、菌落總數在不同溫度的反應速率常數Table1 Reaction rate constants of TVB-N, TBA and total bacterial count at different temperatures

由于TVB-N、TBA、菌落總數與時間(t)成指數關系，因此將三者取自然對數后與時間t進行線性回歸，由線性方程的斜率可得三者在不同溫度下的反應速率常數，見表1。

2.3 反應活化能(Ea)的確定

反應速率常數K與溫度的關系一般符合阿侖尼烏斯(Arrhenius)方程形式：

式中：T為絕對溫度/K；K0為方程常數；Ea為活化能/(J/mol)；R為氣體常數。

對式(4)取自然對數得：

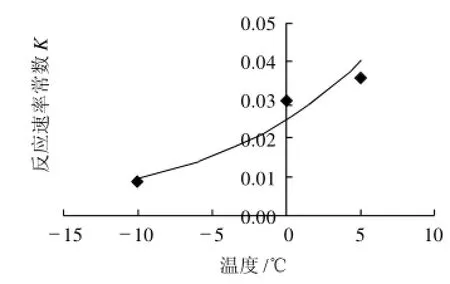
圖4 溫度對TVB-N反應速率常數的影響Fig.4 Effect of temperature on reaction rate constant of TVB-N

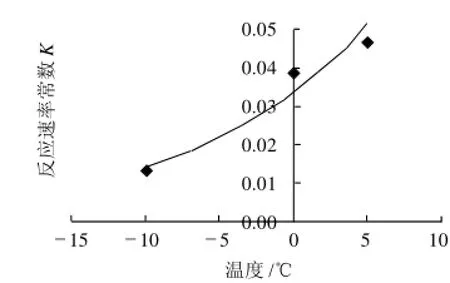
圖5 溫度對TBA反應速率常數的影響Fig.5 Effect of temperature on reaction rate constant of TBA

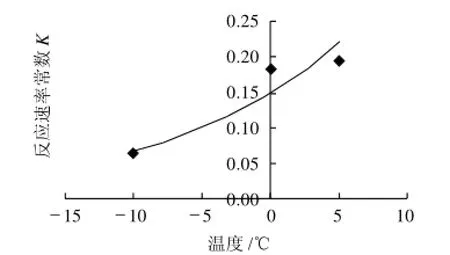
圖6 溫度對菌落總數反應速率常數的影響Fig.6 Effect of temperature on reaction rate constant of total bacterial count

表2 動力學模型參數Table2 Parameters of kinetic models

圖4～6是根據式(4)對速率常數K及溫度T進行回歸[10]。根據式(5)，將不同溫度下的反應速率常數K取自然對數后，對1/T作圖，根據所得直線的斜率可得到Arrhenius方程中的活化能Ea，由直線斜率可得到K0(表2)，相關系數均在0.9以上，能較好的反映卵形鯧鲹的TVB-N、TBA和菌落總數隨時間變化的反應速率常數與貯藏溫度的關系。

2.4 卵形鯧鲹貯藏期的預測模型

2.4.1 TVB-N預測模型

由式(1)和式(4)，可得：

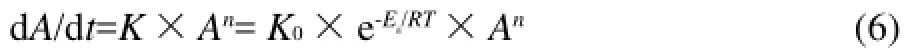
對式(6)積分后，可得貯藏過程中的品質變化通用動力學模型：

根據卵形鯧鲹在貯藏過程中TVB-N的變化，結合公式(7)可得卵形鯧鲹貯藏過程中TVB-N變化的動力學模型：

式中：A0為卵形鯧鲹的初始TVB-N值；At為卵形鯧鲹貯藏t時間后的TVB-N值。

將活化能Ea=56.60kJ/mol，反應常數K0=1.68×109代入式(8)可得：

2.4.2 TBA、菌落總數預測模型

同理可得卵形鯧鲹貯藏過程中TBA變化的動力學模型：

卵形鯧鲹貯藏過程中菌落總數變化的動力學模型：

式(9)、(10)、(11)皆可用來預測卵形鯧鲹在不同貯藏溫度下的貯藏期。

2.5 卵形鯧鲹動力學模型的應用

國標GB 2733—2005《鮮、凍動物性水產品衛生標準》規定，海水魚的TVB-N≤30mg/100g，國外學者研究指出，以細菌菌落總數106CFU/g作為人們消費高品質魚類可接受的限值[11]，細菌數達到107CFU/g或更高時有難聞的氣味和味道產生，即魚類已腐敗變質[12]。TBA值暫未見文獻報道貯藏極限值，本實驗中TBA值達到0.6mg/100g時魚類已變質，因此用此值作為實際可接受的限值來預測貯藏期。根據以上限值對公式(9)、(10)、(11)進行實驗驗證，結果見表3。

由表3可知，通過以上模型預測貯藏期時，實際貯藏期與理論貯藏期較為接近。因此，可根據產品的實際質量要求，利用TVB-N或菌落總數動力學模型，選擇合適的貯藏溫度和貯藏期。

表3 模型的驗證結果Table3 Results of validation of kinetic models

3 結 論

3.1 卵形鯧鲹在貯藏過程中，TVB-N、TBA和菌落總數不斷增加，三者的變化規律均符合一級反應動力學模型，貯藏溫度越高，反應速率越大。

3.2 利用化學動力學原理建立卵形鯧鲹貯藏過程中TVB-N、TBA和菌落總數的動力學模型：t=(lnAt－lnA0)/ (1.68×109×e-56600/RT)，t= (lnAt－lnA0)/(3.10×108× e-52090/RT)，t= (lnAt－lnA0)/(1.87×108×e-47550/RT)。通過以上動力學模型，可根據產品的實際質量要求，選擇合適的貯藏溫度和貯藏期，為生產和銷售提供指導。

[1]齊旭東, 區又君. 卵形鯧鲹不同組織同工酶表達的差異[J]. 南方水產, 2008, 4(3): 38-42.

[2]許鐘, 楊憲時, 郭全友, 等. 冷藏大黃魚貨架期預測模型的建立和評價[J]. 中國水產科學, 2005, 12(6): 779-785.

[3]YOON I H, MATCHES J R, RASCO B. Microbiological and chemical changes of surimi-based imitaition crab during storage[J]. Journal of Food Science, 1998, 53(5): 1343-1346.

[4]KOUTSOUMANIS K P, TAOUKIS P S, DROSINOS E H, et al. Applicability of an arrhenius model for the combined effect of temperature and CO2packaging on the spoilage microflora of fish[J]. Applied and Environmental Microbiology, 2000, 66(8): 3528-3534.

[5]柴春祥. 豬肉品質變化的動力學模型[J]. 食品與發酵工業, 2004, 30 (6): 10-12.

[6]李苗云, 孫靈霞, 周光宏, 等. 冷卻豬肉不同貯藏溫度的貨架期預測模型[J]. 農業工程學報, 2008, 24(4): 235-239.

[7]張麗平, 余曉琴, 童華榮. 動力學模型預測板鴨貨架壽命[J]. 食品科學, 2007, 28(11): 584-586.

[8]鄭寶東, 李怡彬, 張怡, 等. 高透光率青梅濃縮汁貯藏過程顏色的動力學研究[J]. 農業工程學報, 2006, 22(12): 242-244.

[9]van BOEKEL M A J S. Statistical aspects of kinetic modeling for food science problems[J]. Journal of Food Science, 1996, 61(3): 477-485

[10]趙思明, 李紅霞, 熊善柏, 等. 魚丸貯藏過程中品質變化動力學模型研究[J]. 食品科學, 2002, 23(8): 80-82.

[11]ROSNES J T, KLEIBERG G H, SIVERTSVIK M, et al. Effect of modified atmosphere packaging and superchilled storage on the shelf-life of farmed ready-to-cook spotted wolf-fish (Anarhichas minor) [J]. Packaging Technology and Science, 2006, 19(2): 325-333.

[12]許鐘, 楊憲時, 肖琳琳. 低溫貯藏羅非魚微生物學質量變化特性和保藏期[J]. 中國海洋大學學報, 2005, 35(4): 621-625.

Kinetic Model of Quality Change for Trachinotus ovatus during Storage

HUANG Hui，LI Lai-hao*，YANG Xian-qing，HAO Shu-xian，MA Hai-xia，CEN Jian-wei，LI Sha
(South China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences, Guangzhou 510300, China)

Total volatile basic nitrogen (TVB-N), thiobarbituric acid (TBA) and aerobic bacterial count of Trachinotus ovatus at different storage temperatures were investigated. The kinetic models of TVB-N, TBA and aerobic bacterial count were established to predict shelf life and control the quality change of Trachinotus ovatus during storage. Results indicated that TVB-N, TBA and aerobic bacterial count were increased during storage with the increase of storage time and temperature. The reaction model was first order and Arrhenius equation could be used to describe the change of TVB-N, TBA and aerobic bacterial count. The kinetic models of Trachinotus ovatus were t = (lnAt－lnA0)/(1.68×109×e-56600/RT) for TVB-N, t = (lnAt－lnA0)/(3.10×108× e-52090/RT) for TBA, t = (lnAt－lnA0)/(1.87×108×e-47550/RT) for aerobic bacterial count. Therefore, the storage period of Trachinotus ovatus could be calculated using these models.

Trachinotus ovatus；volatile basic nitrogen (TVB-N)；thiobarbituric acid (TBA)；aerobic bacterial count；kinetic model

S984.1；TS254.4；S965.331

A

1002-6630(2010)20-0490-04

2010-06-30

中央級公益性專項資金項目(2009TS14)

黃卉(1980—)，女，助理研究員，博士，研究方向為水產品加工與質量安全。

E-mail：huanghuigd@yahoo.com.cn

*通信作者：李來好(1963—)，男，研究員，博士，研究方向為水產品加工與質量安全。E-mail：laihaoli@163.com