碟形飛行器復合控制系統的控制分配策略研究

劉 鐵，楊 侃，文建國

（海軍航空工程學院 a.飛行器工程系；b.研究生管理大隊；c.科研部，山東 煙臺 264001）

0 引言

現代飛行器由于氣動布局的變化，大多采用多控制面結構，這樣就產生了多種控制面組合方式。如何合理組合多種控制面，使飛行器能適應不同的飛行條件和飛行任務，同時在部分控制面發生故障情況下，仍然能通過剩余控制面的重新組合來協同控制飛行器運動，提高飛行器對故障及損傷的魯棒性，已越來越多的引起國內外科研工作者的關注。

碟形飛行器呈圓盤形，是一種無尾無舵、翼身完全融合的非常規飛行器，它是一個高度非線性的系統，可以采用變質量矩控制與推力矢量控制相結合的方法實現它的飛行控制[1]。變質量矩控制與推力矢量控制構成的復合控制系統可以利用這兩種控制技術的優點，形成復合優勢，實現碟形飛行器的機動飛行控制，但同時也帶來了一系列難題。難題之一就是如何處理一個高度非線性的多輸入系統。論文首先對碟形飛行器的縱向運動方程進行簡化，采用控制分配思想在結構上對碟形飛行器復合控制系統進行了優化，將設計過程分割成控制律設計和分配策略設計兩個部分，再進行控制器設計和控制分配率設計，并進行仿真研究。

1 碟形飛行器縱向通道復合控制模型

通過對碟形飛行器（如圖1所示）所受合外力和力矩的分析可以得到碟形飛行器動質心運動動力學方程、動質心運動學方程、繞動質心轉動的動力學和運動學方程、以及角度關系方程等數學模型，這些非線性方程描述了碟形飛行器的基本運動。限于篇幅，論文不再一一列出。

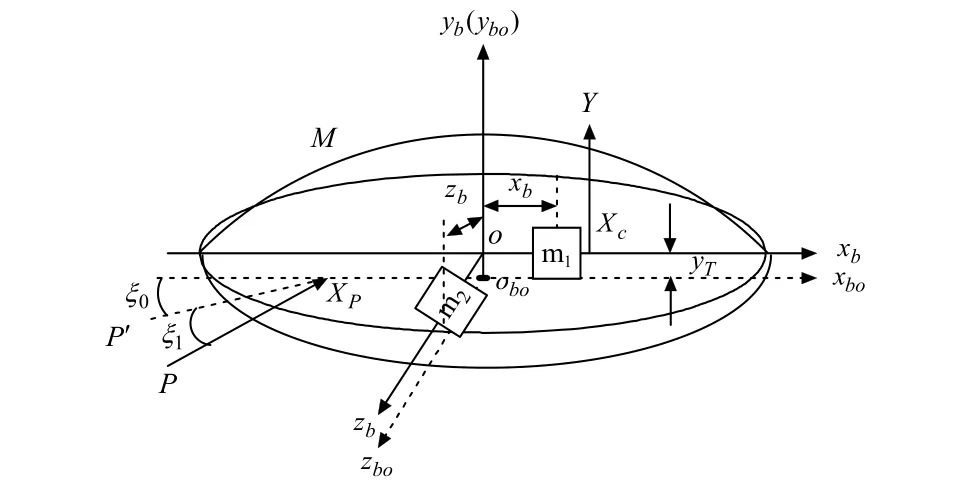
圖1 一類碟形飛行器示意圖

根據縱向運動假設，得到碟形飛行器縱向運動簡化方程[2]

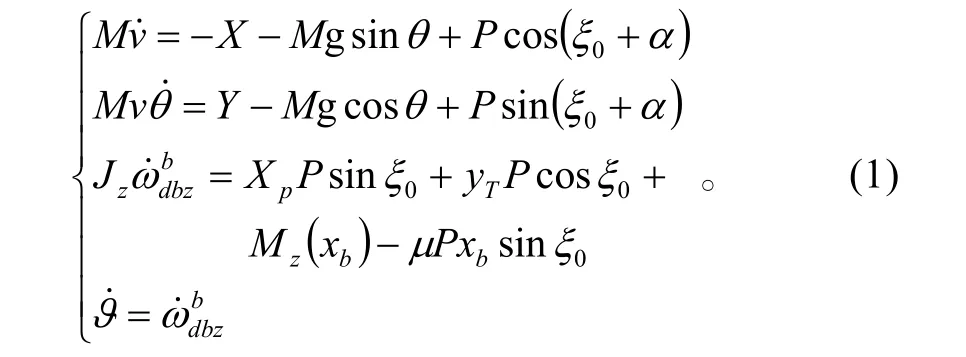
利用小擾動假設，且考慮對速度不進行控制，對式(1)進行小偏差線性化，把簡寫為ωz，得到縱向通道變質量矩/推力矢量復合控制線性化方程

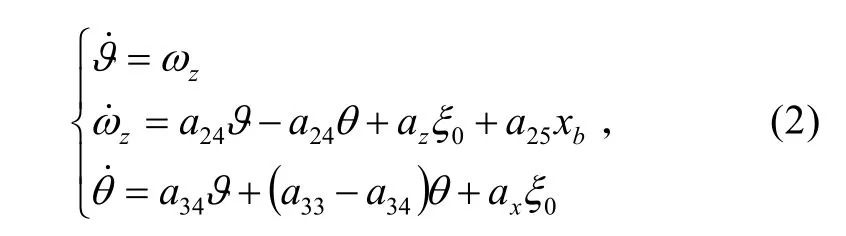
式中：a24、a25、a33、a34、ax和 az為模型線性化后基于基準彈道參數的動力學系數。具體數據由碟形飛行器實物模型的風洞試驗所得。

2 復合控制分配技術簡介

2.1 碟形飛行器復合控制分配系統的結構

碟形飛行器復合控制系統的總體結構如圖2所示：首先，構造一個虛擬控制，針對這個虛擬控制設計控制律；然后，通過復合控制分配策略模塊，將虛擬控制量恰當地分配給兩個控制機構，由兩個控制機構配合共同控制飛行器的姿態運動。按這種設計，控制系統的設計就分割成兩個部分，即控制律設計和分配策略的設計[3-4]。

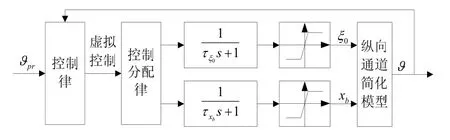
圖2 碟形飛行器復合控制分配系統結構圖

圖2中，控制律的設計仍與一般系統的控制律設計相同。復合控制的分配策略應使整個控制回路從效果上等同于虛擬控制直接作用于系統。因此，對控制分配策略的設計有如下要求：

1）可以根據虛擬控制指令決定單獨或者同時使用各個控制機構；

2）在各個控制進行切換時，不應影響控制器的穩定性。

對于控制分配，國內外的科研工作者取得了很多的研究成果。這些方法歸結起來主要有非優化的控制分配方法和優化的控制分配方法。

2.2 非優化的控制分配方法

非優化的控制分配方法有廣義逆方法、串接鏈方法和直接分配方法等。

2.2.1 廣義逆控制分配方法

廣義逆方法[5-9]包括偽逆法、加權偽逆法及所謂最優的廣義逆分配方法等。偽逆法的思想是取控制量的二次范數（能量函數）為優化指標。即：

式中：B為控制效率矩陣。它的最優解為：u=BT(B BT)?1v=B+v，其中 B+稱為B的偽逆。

偽逆法在所有飛行條件下各個控制量都參與控制，因此可以減少氣動舵面總的偏轉量，延緩質量滑塊位移和推力矢量舵面進入飽和的時間，但是卻可能因為飽和而達不到最大可用力矩。

加權偽逆法是對偽逆法的一種推廣，對于要求的控制力矩，按照使用側重點的不同，對各個控制量進行加權。考慮到控制約束的廣義逆法有多級廣義逆和重新分配偽逆法，這些方法在期望目標可達時，一般可以求出可用的控制，而當期望目標不可達時，誤差將劇烈增大。

2.2.2 串接鏈控制分配方法

串接鏈方法[10-11]將整個操縱面分為若干組，每一組可以產生所期望的力矩。其分配方式描述如下：

將m個控制輸入分為M組，并將相應的控制效率矩陣分為M組，即

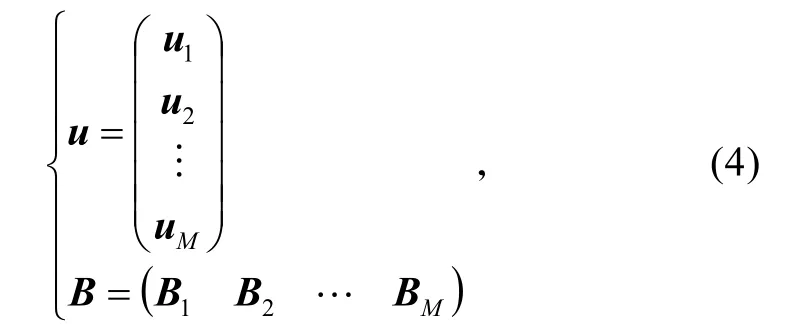
則控制分配問題便是求解下式：

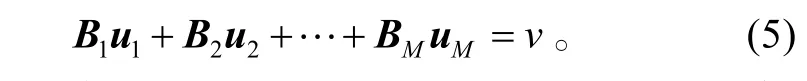
首先用第一組操縱面來實現偽控制輸入v，使得 B1u1=v，如果用第一組不可實現，則依次使用其余組操縱面來是實現控制分配。其過程控制表示：

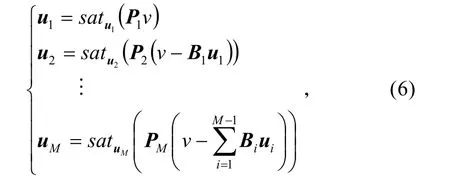
式中：BiPi=I，satui(?)代表第i個操縱面的位置約束和速率約束。

2.2.3 直接分配方法

直接分配方法[12-15]可以描述成如下的最優分配問題：設表示轉矩空間φ 中的單位向量，即

給定控制效率矩陣B，帶約束的控制向量集合? 和期望轉矩向量確定u∈?，使u 產生的轉矩向量在方向上的幅值最大。如果這樣求得的u 產生的轉矩向量的幅值超過了期望轉矩向量的幅值，可對u 乘以一個衰減系數，使兩者相等。其物理意義為：在控制限制范圍內，確定最優控制向量u，使在給定方向上的轉矩最大。

2.3 優化的控制分配方法

2.3.1 基于線性規劃的直接最優分配方法

控制分配的線性規劃問題可描述為如下形式：

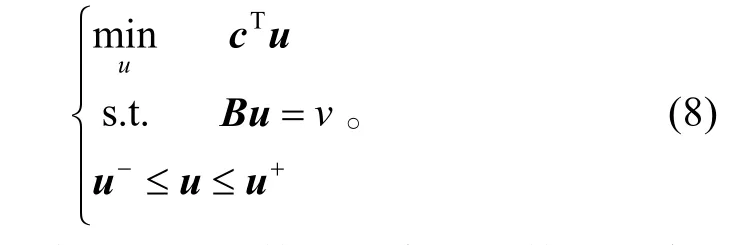
式(8)包括代價函數、等式約束和不等式約束3個重要元素，這里規劃指標取控制量的線性函數，等式約束定義了控制變量的解空間，而不等式約束則體現了執行機構的位置和速率限制。

2.3.2 基于二次規劃的直接最優分配方法

二次規劃方法[16-17]在控制分配中可以表述為：

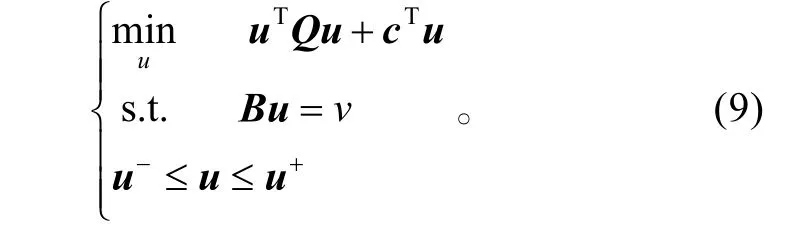
二次規劃方法和線性規劃方法的區別在于代價函數的不同。線性規劃取控制量的線性函數，二次規劃取控制量的二次函數。

當執行機構發生飽和時，滿足條件的最優解位于可達轉矩集之外。此時，求解過程將會放松等式約束，而不等式約束卻保持不變，轉而尋求次優解。二次規劃方法可以靈活利用代價函數和約束條件，對某些控制量進行加權或者懲罰，從而迫使系統遵循其他特定的約束條件，解決復雜控制分配問題。當執行機構出現故障或失效時，二次規劃方法可以同時更新控制效率矩陣B以及等式和不等式約束，使系統重構。例如基于二次規劃方法的方向保持法（Direction Preserving Method）在等式約束不能滿足時，通過引入一個比例系數 0≤σ≤1來修改期望轉矩矢量的大小，但是卻保持期望轉矩矢量的方向，該方向和可達集邊界的交點即為所求解。符號保持法（Sign-Preserving Method）則對于各個軸的期望轉矩分別引入一個比例系數 0≤σi≤1，僅僅改變其中某些期望轉矩的大小，從而構成一個新的期望轉矩矢量，但是符號卻沒有改變，從而更大限度地利用各個控制量。此外，基于頻率加權的二次規劃方法，考慮執行機構的頻率，采用對特定控制量進行頻域加權的方法，可在頻域實現控制量的合理分配。

3 仿真研究

3.1 非優化的控制分配方法

這里僅用廣義逆控制分配方法進行仿真研究。采用PD控制作為虛擬控制。根據文獻[18]知

式中：M是俯仰力矩。

模型的動力學系數見表1。執行機構時間常數0ξτ=0.03 s，bxτ=0.03 s。推力矢量角約束為?30～30°，滑塊滑動距離約束為?0.45～0.45 m。

表1 簡化模型的動力學系數

1）當輸入 ?pr=1°（單位階躍信號）時，單獨控制和復合控制的響應曲線如圖3所示。

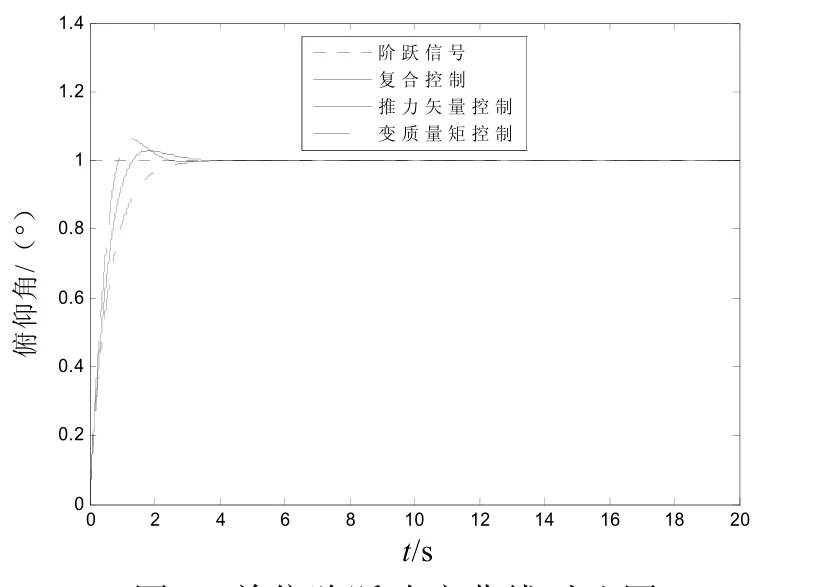
圖3 單位階躍響應曲線對比圖

從圖中可以看出，復合控制的動態性能介于兩者之間。圖4和圖5是控制分配系數變化曲線。

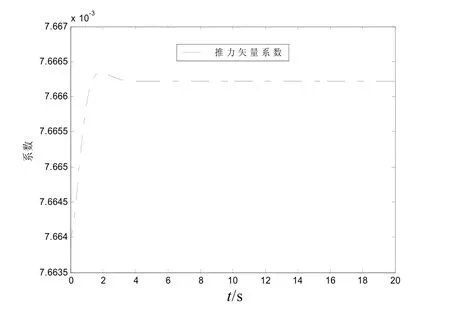
圖4 推力矢量系數變化曲線

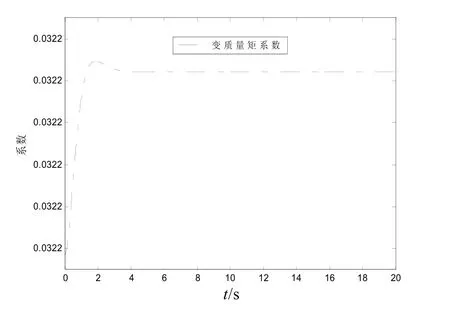
圖5 變質量矩系數變化曲線

從圖4、5中看出，推力矢量系數穩定在0.007 6，而變質量矩系數穩定在0.032 2，大約是推力矢量系數的4倍。

2）考慮控制面發生故障的情況。在t=10 s時，變質量矩控制系統失效，輸入為?pr=1°（單位階躍信號），系統的響應曲線如圖6所示。

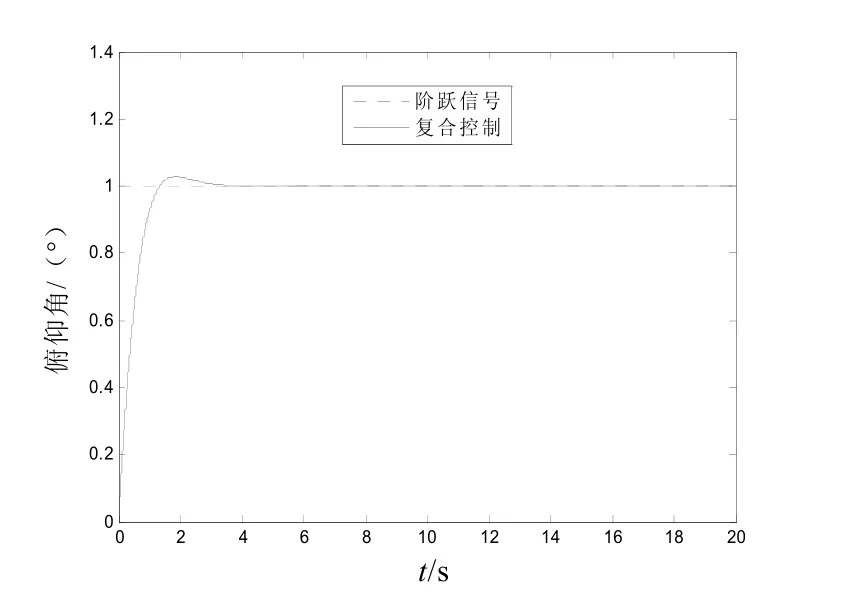
圖6 發生故障情況下單位階躍響應曲線

從圖6中可以看出，故障對控制系統基本沒有產生影響。

圖7和圖8是控制分配系數變化曲線。

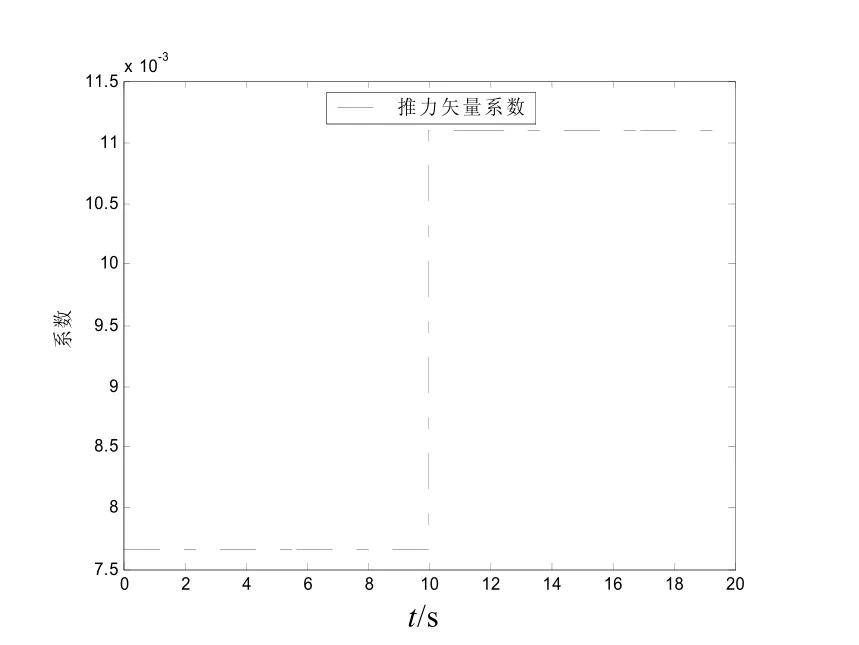
圖7 發生故障情況下推力矢量系數變化曲線

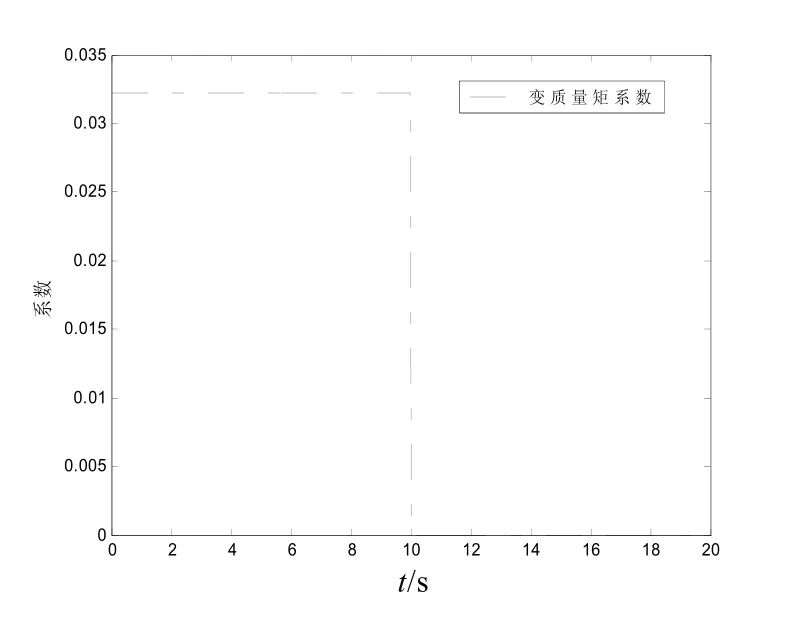
圖8 發生故障情況下變質量矩系數變化曲線

3.2 優化的控制分配方法

這里僅用基于二次規劃的直接最優分配方法進行仿真研究。從2.3.2節分析可知，它本質上是一個目標規劃問題，約束條件Bu=v是一個軟約束，它可以化為一個目標約束，本文用Matlab 中的fgoalattain函數來求解。模型的動力學系數見表1。執行機構時間常數 0ξτ=0.03 s，bxτ=0.03 s。推力矢量角約束為?30°到30°，滑塊滑動距離約束為?0.45m到0.45 m。仿真結構圖如圖2所示。

取Q=I，c=0，當輸入 ?pr=1°（單位階躍信號）時，單獨控制和復合控制的響應曲線如圖9所示。

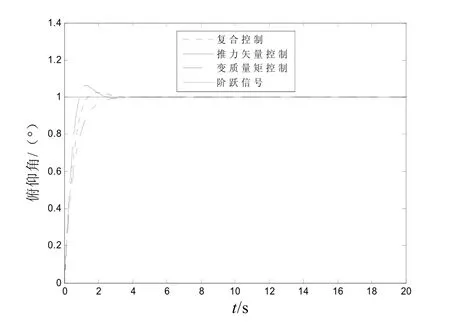
圖9 單位階躍響應曲線對比圖

從圖9中可以看出，與廣義逆控制分配方法類似，復合控制的動態性能介于兩者之間。圖10和圖11是控制分配系數變化曲線。從圖10、11中可以看出，在調節時間內，推力矢量系數大約穩定在0.008，而變質量矩系數大約穩定在0.033 5，這與廣義逆控制方法結果相近；之后，控制分配系數就在穩定值附近小幅震蕩。

控制量變化曲線如圖12、13所示。

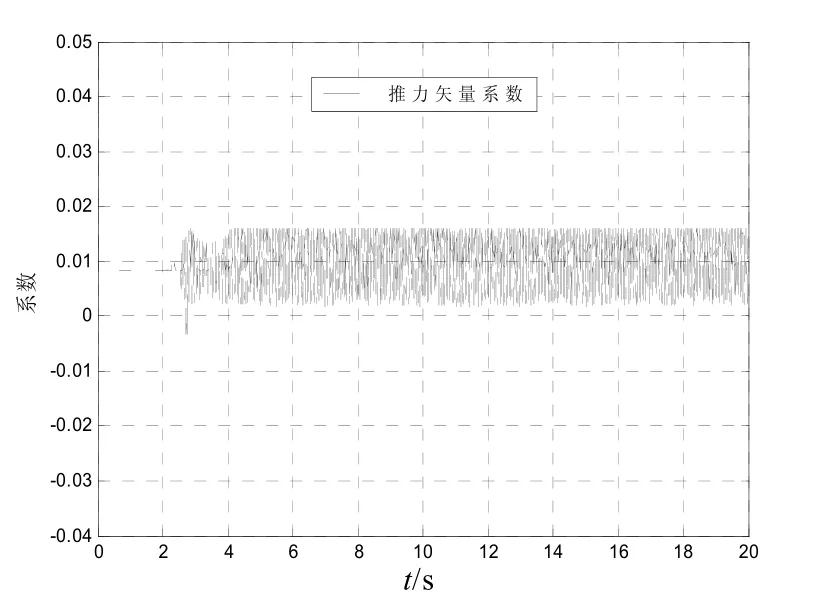
圖10 推力矢量系數變化曲線

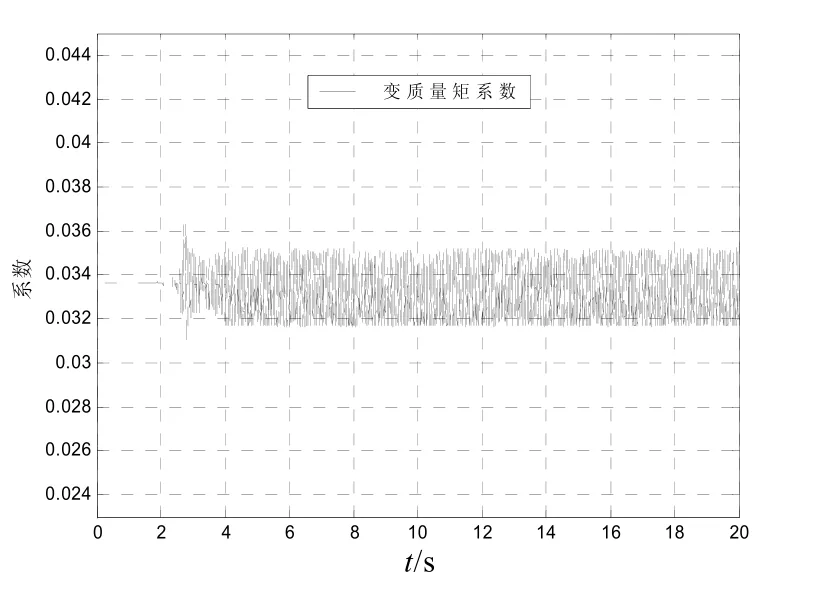
圖11 變質量矩系數變化曲線

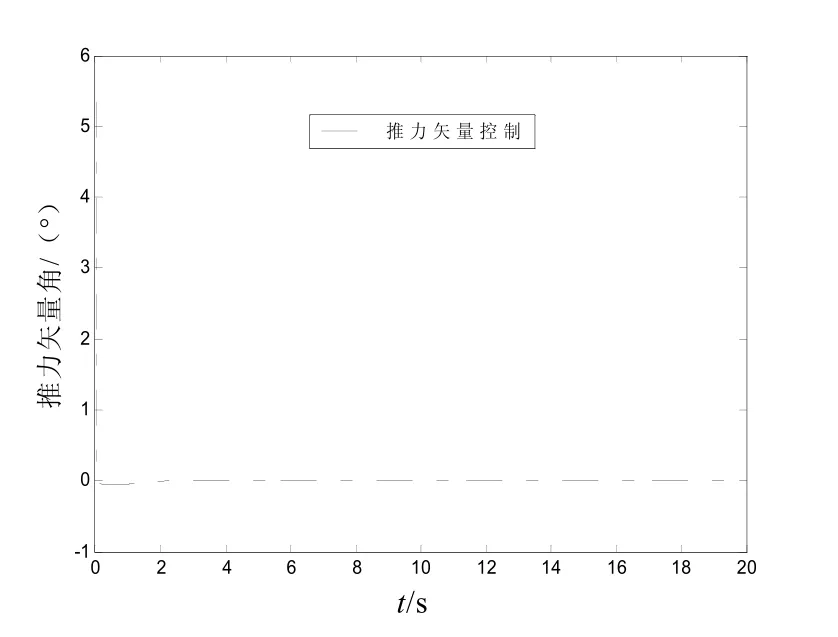
圖12 推力矢量控制的控制量變化曲線

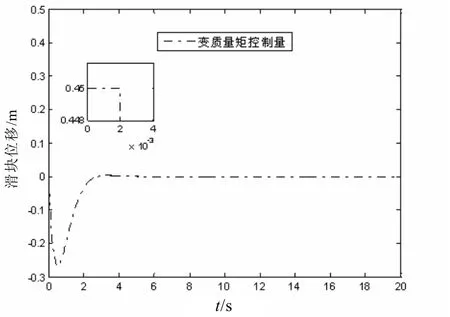
圖13 變質量矩控制的控制量變化曲線

從圖13中可以看出，變質量矩控制在初期有一段飽和狀態，且在整個控制過程中占主導地位。

4 結論

本文采用控制分配思想在結構上對碟形飛行器復合控制系統進行了優化，將設計過程分割成控制律設計和分配策略設計兩個部分，分別采用了廣義逆控制分配方法和基于二次規劃的直接最優分配方法進行了仿真研究，兩種方法各有優缺點：廣義逆控制分配方法原理簡單，解算速度快，便于實時控制，但它沒有考慮約束條件的影響；基于二次規劃的直接最優分配方法在求解的過程中已經考慮了控制量的飽和約束，所以在仿真的過程中不用加飽和環節，簡化了控制系統的結構，但它的求解時間較長，在實際應用中，可能達不到實時控制的要求。

[1]王軍生,徐勝紅,劉海波,等.碟形飛行器復合控制分配策略的設計與分析[J].戰術導彈技術,2006(3):69-73.

[2]馮國虎.碟形飛行器復合控制中的控制分配策略[J].系統仿真學報,2008,20(4):970-973.

[3]徐勝紅,盛忠培,顧文錦.碟形飛行器復合控制的非線性分配策略研究[J].彈箭與制導學報,2006,26(1):8-11.

[4]程鳳舟,萬自明,陳士櫓,等.防空導彈直接力與氣動力復合控制系統設計[J].飛行力學,2003,21(2):49-52.

[5]RANEY D L,MONLNOMERY R C.Flight control using distributed shape-chance effector arrays[R].AIAA-2000-1560,2000.

[6]REINELSPERNERW C.BANDA S S.Nonlinear simulation of a modified F-16 with full-envelope control law[J].Control Engineering Practice,1998,17(6):309-320.

[7]BORDINNON K.Constrained control allocation for systems with redundant control effectors[D].Blacksburg.VA:Virninia Polytechnic Institute and State University.1996.

[8]EBERHARDT R,WARD D.Indirect adaptive flight control of a tailless fighter aircraft[C]//Proceedings of the AIAA Guidance,Control,and Dynamics Conference.Portland.OR,1999:466-476.

[9]VIRNIG J,BODDEN D.Multivariable control allocation and control law conditioning when control effectors limit[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference.Scottsdale,AZ,1994:572-582.

[10]BUFFINGTON J M,ENNS D F.Lyapunov stability analysis of daisy chain control allocation[J].Journal of Guidance,Control,and Dynamics,1996,19(6):1226-1230.

[11]TEEL A R,BUFFINGTON J M.Anti-windup for an F-16's daisy chain control allocate[R].AIAA-1997-3606.1997.

[12]DURHAM W C.Constrained control allocation[J].Journal of Guidance,Control,and Dynamics,1993,16(4):717-725.

[13]DURHAM W C.Attainable moments for the constrained control allocation problem[J].Journal of Guidance,Control,and Dynamics,1994,17(6):1371-1373.

[14]DURHAM W C.Computationally efficient control allocation[J].Journal of Guidance,Control and Dynamics,2001,24(3):519-524.

[15]PELERSEN J,BODSON M.Fast control allocation using spherical coordinates[R].AIAA-1999-4215.1999.

[16]PELERSEN J,BODSON M.Constrained quadratic programming techniques for control allocation[C]//Proceedings of the 42ndIEEE Conferences on Decision and Control.Maui,Hawaii,USA,2003.

[17]SIMMONS A T.Control allocation techniques using existing and novel quadratic programming algorithms[D].Auburn University,2003.

[18]MICHAEL W OPPENHEIMER,DAVID B DOMAN.A method for including control effector interactions in the control allocation problem[R].AIAA-2007-6418.2007.