支持向量機原理及展望

陳冰梅，樊曉平，周志明，李雪榮

CHEN Bing-mei1,2, FAN Xiao-ping1, ZHOU Zhi-ming3, LI Xue-rong2

（1. 中南大學 信息科學與工程學院，長沙 410083；2. 中南大學 湘雅二醫院，長沙 410011）3. 長沙環境保護職業技術學院，長沙 410004）

支持向量機原理及展望

The principle and prospect of support vector machine

陳冰梅1,2，樊曉平1，周志明3，李雪榮2

CHEN Bing-mei1,2, FAN Xiao-ping1, ZHOU Zhi-ming3, LI Xue-rong2

（1. 中南大學 信息科學與工程學院，長沙 410083；2. 中南大學 湘雅二醫院，長沙 410011）3. 長沙環境保護職業技術學院，長沙 410004）

支持向量機(SVM)是90年代中期發展起來的基于統計學習理論的一種機器學習方法，通過尋求結構化風險最小來提高學習機泛化能力，實現經驗風險和置信范圍的最小化，從而達到在統計樣本量較少的情況下，亦能獲得良好統計規律的目的。該方法不但算法簡單,而且具有較好的“魯棒”性，與神經網絡相比，它的優點是訓練算法中不存在局部極小值問題，在解決小樣本、非線性及高維模式識別問題中表現出許多特有的優勢，并能夠推廣應用到函數擬合等其他機器學習問題中，現在已經在許多領域取得了成功的應用。

支持向量機；神經網絡；分類器；核函數

0 引言

支持向量機(Support Vector Machine,SVM)是由Vapnik領導的AT&TBell實驗室研究小組在1963年提出的一種新的非常有潛力的分類技術，SVM是一種基于統計學習理論的模式識別方法，主要應用于模式識別領域。由于當時這些研究尚不十分完善，在解決模式識別問題中往往趨于保守，且數學上比較艱澀，這些研究一直沒有得到充分的重視。直到90年代，統計學習理論 (Statistical Learning Theory，SLT)的實現和由于神經網絡等較新興的機器學習方法的研究遇到一些重要的困難，比如如何確定網絡結構的問題、過學習與欠學習問題、局部極小點問題等，使得SVM迅速發展和完善，在解決小樣本、非線性及高維模式識別問題中表現出許多特有的優勢，并能夠推廣應用到函數擬合等其他機器學習問題中，從此迅速的發展起來，現在已經在許多領域取得了成功的應用。

1 基本原理

假設如圖1這些數據點是n維實空間中的點。我們希望能夠把這些點通過一個n-1維的超平面分開。通常這個被稱為線性分類器。有很多分類器都符合這個要求。但是我們還希望找到分類最佳的平面，即使得屬于兩個不同類的數據點間隔最大的那個面，該面亦稱為最大間隔超平面。如果我們能夠找到這個面，那么這個分類器就稱為最大間隔分類器。

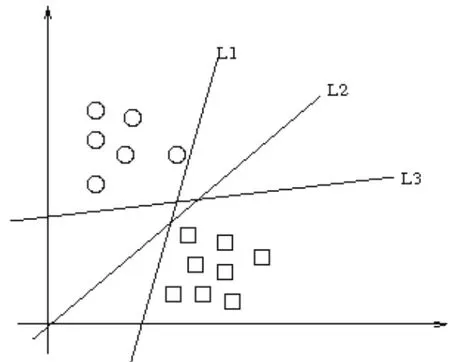
圖1 多種分類超平面示意圖

如圖1有很多個分類器(超平面)可以把數據分開，但是只有一個能夠達到最大分割。

支持向量機將向量映射到一個更高維的空間里，在這個空間里建立有一個最大間隔超平面。在分開數據的超平面的兩邊建有兩個互相平行的超平面。建立方向合適的分隔超平面使兩個與之平行的超平面間的距離最大化。假定平行超平面間的距離或差距越大，分類器的總誤差越小。

支持向量機屬于一般化線性分類器。他們也可以認為是提克洛夫規則化（Tikhonov Regularization）方法的一個特例。這種分類器的特點是他們能夠同時最小化經驗誤差與最大化幾何邊緣區。因此支持向量機也被稱為最大邊緣區分類器。

所謂支持向量是指那些在間隔區邊緣的訓練樣本點。 這里的“機（machine,機器）”實際上是一個算法。在機器學習領域，常把一些算法看做是一個機器。

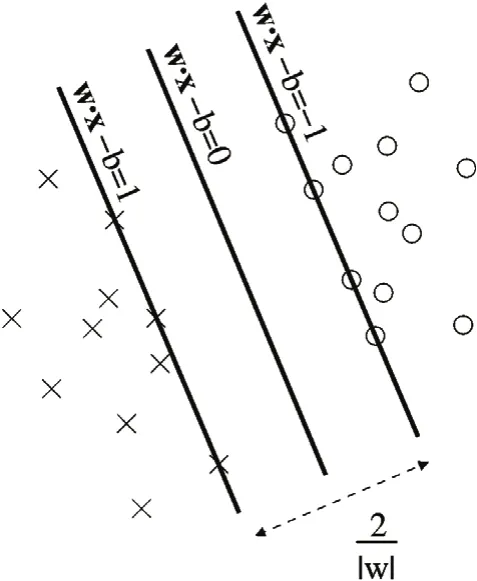
圖2 在超平面上的樣本點也稱為支持向量

如圖2設樣本屬于兩個類，用該樣本訓練svm得到的最大間隔超平面。在超平面上的樣本點也稱為支持向量，支持向量機方法是建立在統計學習理論的VC 維理論和結構風險最小原理基礎上的，根據有限的樣本信息在模型的復雜性（即對特定訓練樣本的學習精度）和學習能力（即無錯誤地識別任意樣本的能力）之間尋求最佳折衷，以期獲得最好的推廣能力 。

支持向量機(Support vector machines，SVM)與神經網絡類似，都是學習型的機制，但與神經網絡不同的是SVM使用的是數學方法和優化技術。

2 支持向量機的算法

SVM的支持向量機的主要思想可以概括為兩點:

1）它是針對線性可分情況進行分析，對于線性不可分的情況,通過使用非線性映射算法將低維輸入空間線性不可分的樣本轉化為高維特征空間使其線性可分，從而使得高維特征空間采用線性算法對樣本的非線性特征進行線性分析成為可能；

2）它基于結構風險最小化理論之上在特征空間中建構最優分割超平面，使得學習器得到全局最優化，并且在整個樣本空間的期望風險以某個概率滿足一定上界。

支持向量機的目標就是要根據結構風險最小化原理，構造一個目標函數將兩類模式盡可能地區分開來，通常分為兩類情況來討論：線性可分與線性不可分。

2.1 線性可分情況

在線性可分的情況下，就會存在一個超平面使得訓練樣本完全分開，該超平面可描述為:

w ·x + b = 0 (1)

其中，“·”是點積, w是n維向量, b為偏移量。

最優超平面是使得每一類數據與超平面距離最近的向量與超平面之間的距離最大的這樣的平面，最優超平面可以通過解下面的二次優化問題來獲得：

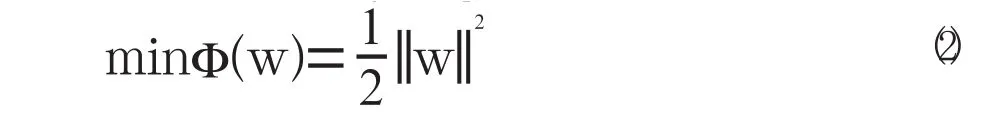
滿足約束條件：

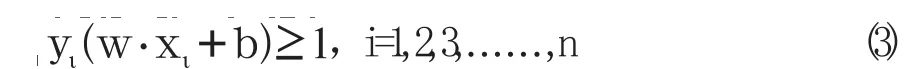
在特征數目特別大的情況，可以將此二次規劃問題轉化為其對偶問題：

滿足約束條件：

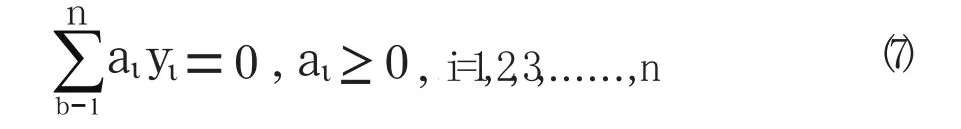
這里α=(α1,...,αn)是Lagrange 乘子，b*是最優超平面的法向量， 是最優超平面的偏移量,在這類優化問題的求解與分析中，KKT條件將起到很重要的作用，在(7) 式中,其解必須滿足：

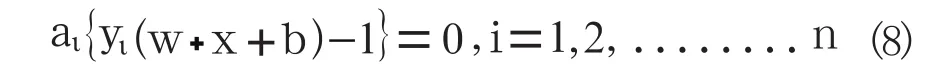
從式(5)可知,那些aι=0的樣本對分類沒有任何作用，只有那些aι>0的樣本才對分類起作用，這些樣本稱為支持向量，故最終的分類函數為：

根據f (x)的符號來確定X 的歸屬。

2.2 線性不可分的情況

對于線性不可分的情況,可以把樣本X 映射到一個高維特征空間H，并在此空間中運用原空間的函數來實現內積運算，這樣將非線性問題轉換成另一空間的線性問題來獲得一個樣本的歸屬，根據泛函的有關理論，只要一種核函數滿足Mercer條件,它就對應某一空間中的內積，因此只要在最優分類面上采用適當的內積函數就可以實現這種線性不可分的分類問題。此時的目標函數為：

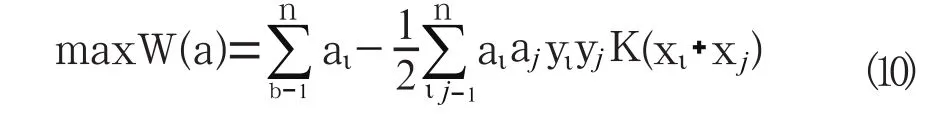
其相應的分類函數為:

2.3 內積核函數

SVM的關鍵在于核函數。低維空間向量集通常難于劃分，解決的方法是將它們映射到高維空間。但這個辦法帶來的困難就是計算復雜度的增加，而核函數正好巧妙地解決了這個問題。也就是說，只要選用適當的核函數，就可以得到高維空間的分類函數。在SVM理論中，采用不同的核函數將導致不同的SVM算法。目前有三類用的較多的內積核函數：第一類是

我們所能得到的是p階多項式分類器，第二類是徑向基函數（RBF），也稱作高斯核函數：

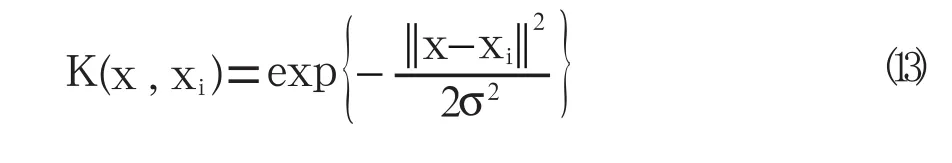
第三類是Sigmoid函數：

這時SVM實現的就是包含一個隱層感知器，隱層結點數是由算法自動確定的。究竟用哪一種核函數比較好，這還是取決你對數據處理的要求，不過建議可以使用徑向基函數。

3 支持向量機的特點

1）它是專門針對有限樣本情況的，其目標是得到現有信息下的最優解而不僅僅是樣本數趨于無窮大時的最優值；

2）算法最終將轉化成為一個二次型尋優問題，從理論上說，得到的將是全局最優點，解決了在神經網絡方法中無法避免的局部極值問題；

3）算法將實際問題通過非線性變換轉換到高維的特征空間(Feature Space)，在高維空間中構造線性判別函數來實現原空間中的非線性判別函數，特殊性質能保證機器有較好的推廣能力，同時它巧妙地解決了維數問題，其算法復雜度與樣本維數無關；

4）在SVM方法中，只要定義不同的內積函數，就可以實現多項式逼近、貝葉斯分類器、徑向基函數(Radial Basic Function或RBF)方法、多層感知器網絡等許多現有學習算法。

5）該方法不但算法簡單,而且具有較好的“魯棒”性。

4 結束語

支持向量機算法是一個凸二次優化問題,能夠保證找到的極值解就是全局最優解，是神經網絡領域取得的一項重大突破。與神經網絡相比，它的優點是訓練算法中不存在局部極小值問題，可以自動設計模型復雜度(例如隱層節點數)，不存在維數災難問題，泛化能力強，SVM已初步表現出很多優于已有方法的性能。 SVM正在成為繼神經網絡研究之后新的研究熱點，并將推動機器學習理論和技術有重大的發展。

支持向量機能非常成功地處理回歸問題(時間序列分析)、模式識別(分類問題、判別分析)、 概率密度函數估計等諸多問題，并可推廣于預測和綜合評價等領域，例如，在模式識別方面，對于手寫數字識別、語音識別、人臉圖像識別、文章分類等問題，SVM算法在精度上已經超過傳統的學習算法或與之不相上下。目前國際上支持向量機理論研究和實際應用兩方面都正處于飛速發展階段。

[1] B.E.Boser,I.M.Guyon,and V.N.Vapnik. A training algorithm for optimal margin classifiers.In D.Haussler, editor,5th Annual ACM Workshop on COLT,pages 144-152,Pittsburgh,PA,1992.ACM Press.

[2] Corinna Cortes and V.Vapnik,"Support-Vector Networks,Machine Learning,20,1995,1.

[3] 張艷.一類基于支持向量機的軟件故障預測方法[J].小型微型計算機系統,2010.31(7):1380-1383.

[4] 杜樹新,吳鐵軍.模式識別中的支持向量機方法[J].浙江大學學報(工學版), 2003,9,37(5):521-526.

[5] 劉渤海.基于ANN和SVM的質量預測方法研究[J].制造業自動化,2010.32(5):152-155.

[6] 韋抒.應用支持向量機實現轉子故障的模式分類[J].制造業自動化,2009.31(7):82-85.

TP273

A

1009-0134(2010)12(上)-0136-03

10.3969/j.issn.1009-0134.2010.12(上).45

2010-08-17

國家自然科學基金題（39270262）

陳冰梅（1963 -），女，廣西玉林人，高級，工程師，在讀博士，研究方向為人工智能和智能計算。