灰色GM(1，1)模型在氯離子濃度模擬中的應用

應敬偉 陳賀功

1 氯離子濃度變化模擬的意義

在沿海地區(qū)，鋼筋混凝土結(jié)構(gòu)耐久性的主要影響因素是氯離子的侵蝕，海洋是氯離子的主要來源，對沿海鋼筋混凝土結(jié)構(gòu)而言，其構(gòu)件一般直接或間接地遭受海水侵蝕，且與海風、臺風、海霧、海潮、海砂中攜帶的氯離子含量有關，沿海混凝土中的氯離子濃度變化的影響因素復雜，因此研究氯離子濃度沿混凝土深度的變化規(guī)律對正確評估鋼筋混凝土的耐久性具有重要意義。針對氯離子濃度在沿海混凝土中的分布規(guī)律，一些學者基于Fick第二擴散定律提出各自的混凝土中氯離子濃度變化的分析方法[1-4]，但Fick第二擴散定律是基于飽和溶液濃度梯度的單一因素推導出來的，因此對于海洋干濕交替環(huán)境下氯離子在混凝土中的變化并不完全符合該定律。通過對Fick第二擴散定律的方程進行修正，可以得到更加符合試驗結(jié)果的模型[2，5]。衛(wèi)軍通過最小二乘擬合出氯離子濃度隨深度的變化特征[6]，由于氯離子的濃度一般是按照進深7 mm取值，在保護層內(nèi)氯離子濃度沿著深度的變化只能取若干有限的數(shù)據(jù)，不能使用統(tǒng)計方法來分析，而灰色系統(tǒng)理論擅長于少數(shù)據(jù)的分析[7]，因此筆者采用灰色系統(tǒng)理論對混凝土中氯離子濃度沿著深度的變化進行模擬更加具有合理性。

2 灰色GM(1，1)模型介紹

灰色系統(tǒng)理論是由鄧聚龍創(chuàng)立并由劉思峰等學者發(fā)展的一門新興的邊緣學科，灰理論極強的滲透性使其在不同領域有著廣泛的應用[7]。GM(1，1)模型是灰理論的核心部分，其他類似模型均是基于其建立的。

設原始序列:

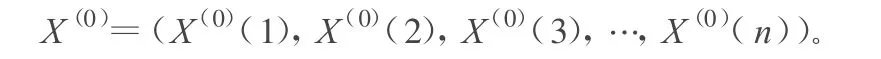
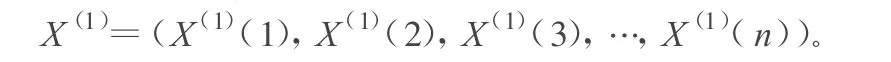
X(1)(k)可建立下述白化方程:

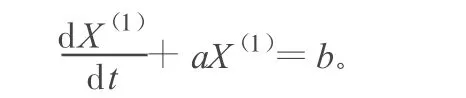
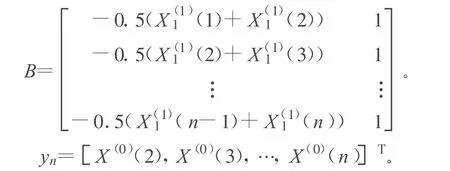
白化微分方程的解為:

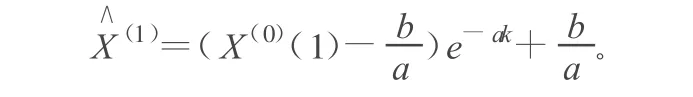
稱其為GM(1，1)的預測響應式，其還原值為:

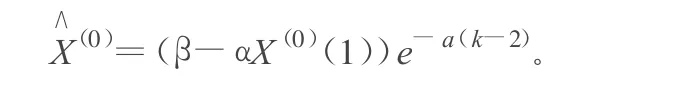
或?qū)懽?

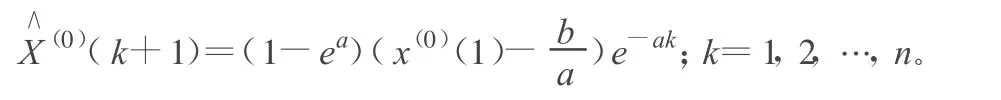
在GM(1，1)模型中，-a為發(fā)展系數(shù)，b為灰色作用量。-a實際上反映了與的發(fā)展勢態(tài)。

3 GM(1，1)模型的適用條件

3.1 準光滑性

任何一種理論只有滿足其一定的前提條件才成立，灰色序列必須滿足光滑性條件才適合GM(1，1)模型，即需要滿足函數(shù)的光滑和連續(xù)的條件，因灰色序列的數(shù)據(jù)是離散的，不能求導，故序列的光滑性不能用導數(shù)確定。然而通過光滑比可以從另一個角度反映序列的光滑性，序列 x的光滑比定義為:

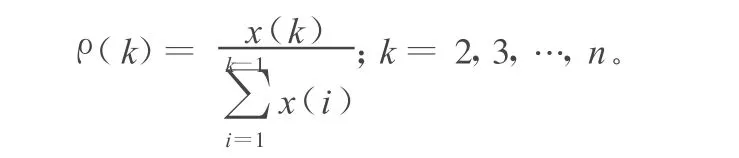
若序列x滿足:

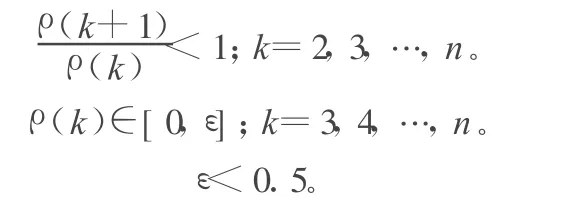
則稱x為光滑序列。

3.2 準指數(shù)規(guī)律

準指數(shù)規(guī)律是灰色建模的基礎，因此灰色序列 x還需要滿足準指數(shù)規(guī)律。對于灰色序列 x:?k，σ(k)∈[a，b]，b-a=δ。稱序列 x具有絕對灰度為δ的灰指數(shù)規(guī)律;當δ＜0.5時，稱 δ具有準灰指數(shù)規(guī)律。

4 工程實例分析

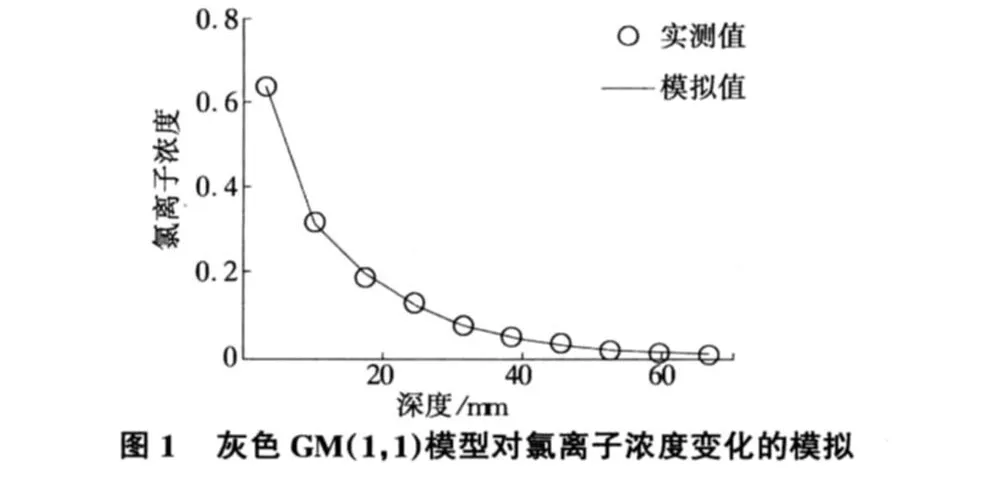
對嘉興港一碼頭進行氯離子濃度檢測，檢測進深為7 mm，氯離子濃度由淺到深的分布為表1中的實測數(shù)據(jù)[8]。光滑比在[0，0.5]范圍內(nèi)時即為準光滑序列，灰指數(shù)在[1，1.5]范圍內(nèi)時即為滿足準灰指數(shù)規(guī)律[7]。由表1中的光滑比、灰指數(shù)可知實測數(shù)據(jù)序列適用于GM(1，1)建模。計算后的各個數(shù)據(jù)見表1。實測值與模擬值的比較如圖1所示。

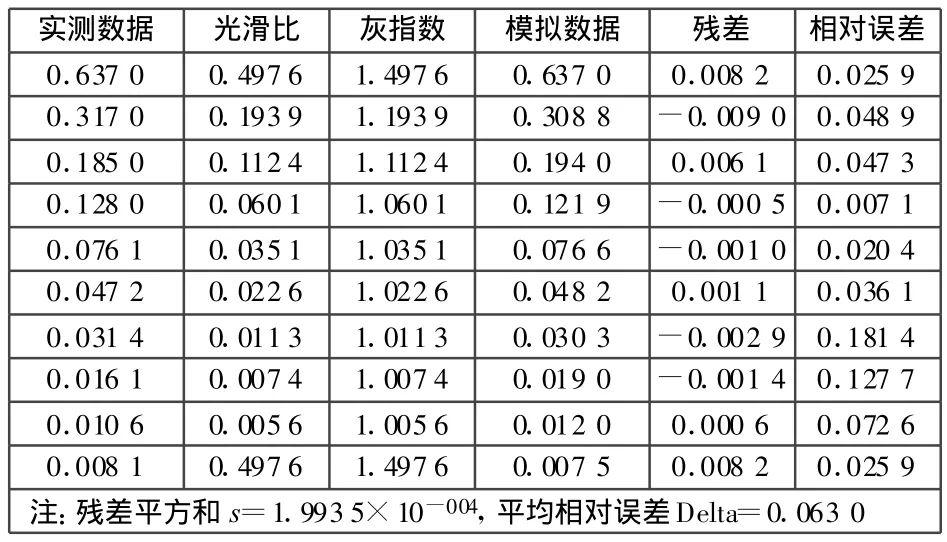
表1 誤差檢驗表

由表1，圖1可知:平均相對誤差為6%。由于殘差尾段未出現(xiàn)4個連續(xù)同號情況，故不適合繼續(xù)用殘差模型來進一步調(diào)高精度，說明采用GM(1，1)模型模擬已經(jīng)達到了最佳逼近的程度。

[1] 吳相豪.預估海港工程混凝土氯離子濃度分布新方法[J].水利水運工程學報，2006(1):20-23.

[2] 孟憲強，王顯利，王凱英，等.海洋環(huán)境混凝土中氯離子濃度預測的多系數(shù)擴散方程[J].武漢大學學報(工學版)，2007，40(3):40-42.

[3] 于林軍，榮艷倩，劉文光.基于氯離子濃度的混凝土構(gòu)件耐久性壽命預測[J].黑龍江科技信息，2009(30):48-50.

[4] 吳相豪，李 麗，Xianghao WV，等.海港碼頭混凝土構(gòu)件氯離子濃度預測模型[J].上海海事大學學報，2006，27(1):28-30.

[5] 吳 瑾，吳勝興.海洋環(huán)境下混凝土中鋼筋表面氯離子濃度的隨機模型[J].河海大學學報(自然科學版)，2004，32(1):30-32.

[7] 劉思峰，謝乃明.灰色系統(tǒng)理論及其應用[M].北京:科學出版社，2008.

[8] 姚昌建.沿海碼頭混凝土設施受氯離子侵蝕的規(guī)律研究[D].杭州 :浙江大學 ，2007.