信息熵模糊層次分析在橋梁方案比選中的應用

林 彬

現在信息熵模糊層次分析理論在農業、經濟及管理等眾多領域的應用中已取得了可喜的效果。在土木工程建設中的應用還是近幾年的事情，而在橋梁工程建設中的應用卻更為少見。眾所周知，在橋梁工程設計方案的優選中需要考慮使用功能、技術、經濟、美觀和社會等諸方面的效果進行綜合論證，從提出的諸方案中進行選擇。在這一過程中會發現，有些信息或指標如直接工程造價、臨時工程費、工期等可通過計算成為已知信息。但有不少因素及指標如施工難度、橋梁美觀、通航要求等只能定性描述是非量化的灰數，這就給方案的評價和優選帶來了困難。事實上，橋梁方案比選用信息熵模糊層次分析方法可獲得較滿意的結果[1]。

1 項目概況

1.1 信息熵

信息熵是系統有序程度度量。信息熵計算公式為:

其中，xi為隨機事件獨立出現的可能狀態;p(xi)為某一狀態出現的概率。對數的底取為e時，其單位為奈特(Nat);取為10時，其單位是哈特(Hartley)。

1.2 信息熵模糊物元

模糊物元系指用有序三元組(事物、特征、模糊量值)來描述事物的基本元。如果模糊物元中事物為方案，特征為信息熵，則稱為信息熵模糊物元，記為 RH。若信息熵模糊物元中有 n個方案，則稱為 n個方案的信息熵模糊物元，記為 RnH。

1.3 層次分析

層次分析是把復雜的決策問題分成若干層次，形成遞階層次結構，并根據一定的數量規則給出各層次的指標判斷矩陣，然后，利用數學方法對其可信性、正確性進行驗證[2]。

2 橋梁方案比選模型

2.1 模糊層次結構模型

層次分析結構模型是根據影響橋梁方案的諸多因素之間的相互聯系及隸屬關系來構造的，它包括目標層、準則層和指標層。就每一層次的相對重要性給出定量的表示，如圖1所示。

2.2 信息熵模糊層次評價模型

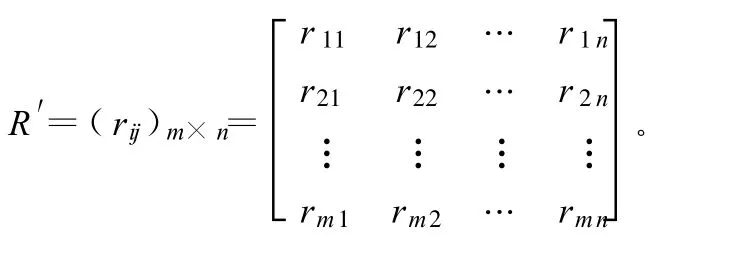
利用層次分析法，求出各評價指標的主觀權重 wi，再結合熵權構成綜合的權重 Wi，即可進行信息熵模糊層次評價。在橋梁方案比選過程中，當有n個方案時，若用m項指標及其相應量值來描述，則構成為n個方案 m維矩陣，記為 R，然后將各分指標通過適當的變化(如向量歸一化、線性比例變換、極差變換等方法)進行標準化，使其均勻落在統一的無量綱區間。一般而言，指標可以分為效益型指標(越大越優型)、成本型指標(越小越優型)、固定型指標(越接近某一理想B越優型)以及區間型指標(期望區間[a1，a2]越優型)，本文采用極差變換法，對各類指標無量綱化。

1)對于效益型指標:

2)對于成本型指標:

3)對于固定型指標:

4)對于區間型指標:

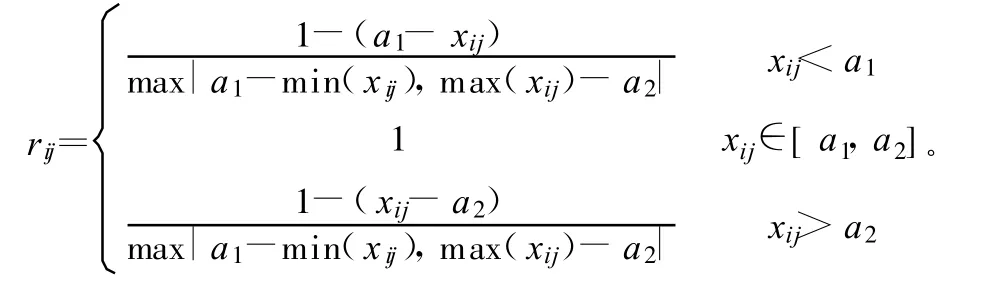
3 應用實例

廣西融水水東大橋位于融水苗族自治縣東南部，融江水在橋位段接近北南流向，橋位段緊鄰拉沙洲，約有1 km順直段后緊接河灣，橋位段屬穩定河段，呈U形，兩岸為一級階地，西岸為融水縣城區，東岸為水東城區。

根據橋址的自然地理情況，擬定5個橋型方案進行比選，其相應的技術經濟指標數值和定性評價如表1所示。

根據各個方案的技術、經濟和美觀等多方面的模糊層次結構模型，通過對過去工程資料的分析、專家咨詢、理論計算，確定的判斷矩陣A為:

表1 擬選方案的技術經濟指標

用方根法計算，特征向量Rw=[0.276 8 0.189 7 0.189 7 0.126 5 0.086 2 0.059 9 0.031 6 0.022 8 0.016 8]T。特征根 λmax=9.376 9，CR=CI/RI=0.047＜0.10時，結果滿足一致性。

根據表1數值，可建立橋梁方案特征矩陣:

其中承載潛力、橋梁美觀和通航要求屬效益性指標，其他均屬成本型指標，根據極差變化法原則，可得標準化處理后的特征矩陣為:

將判斷矩陣A和標準化后的方案特征矩陣代入可得信息熵復合矩陣:

H=[0.468 4 0.359 3 0.438 1 0.643 40.602 8]。

從計算結果可以看出，5個擬選橋梁方案的優劣順序為n4＞n5＞n1＞n3＞n2，方案4號為最優方案。

[1] 王 成.灰色理論在橋梁方案比選中的應用[J].重慶交通學院學報，1999，18(4):125-129.

[2] 王廣月.深基坑支護決策的信息熵模糊層次分析模型[J].巖土力學，2004，25(5):737-739.

[3] 張鐵夫.熵權模糊綜合評價法在工程機械選優決策中的應用[J].礦山機械，2004，36(4):70-73.

[4] 趙 剛.基于熵權的建筑方案模糊優選模型[J].華北水利水電學院學報，2008，29(4):97-99.

[5] 羅君君.熵權決策法在公路工程評標中的應用[J].佳木斯大學學報，2007，25(1):28-30.