基于馬爾可夫鏈的EWMA控制圖參數優化及其實現

白雙梅，杜福洲

（北京航空航天大學 機械工程及自動化學院，北京 100191）

基于馬爾可夫鏈的EWMA控制圖參數優化及其實現

白雙梅，杜福洲

（北京航空航天大學 機械工程及自動化學院，北京 100191）

0 引言

SPC是一種借助數理統計理論的過程質量控制方法，通常采用控制圖來達到過程控制的目的。

傳統的休哈特控制圖的統計變量只與當前觀測值相關，而忽略大量過程歷史數據中包含的信息，因此，傳統的休哈特控制圖對小偏移過程不敏感，往往會造成漏判情況的出現。為此，研究者們提出了累積和（CUSUM）控制圖和指數加權滑動平均（EWMA）控制圖來實現對小偏移過程的監控。

EWMA控制圖的性能取決于參數（平滑系數λ、控制線參數L）的選取，因此，EWMA控制圖參數的選取直接影響控制圖對小偏移過程的控制效果。有關控制圖參數優化問題日益引起廣泛關注，相關研究人員曾提出以田口質量損失函數最小為目標的CUSUM控制圖優化設計方法，應用馬爾可夫鏈研究了多元指數移動平均控制圖及MCUSUM控制圖中ARL計算的數學模型[1～3]，設計監控EWMA控制圖均值和方差的經濟控制圖[4]，在文獻[5]中基于馬爾可夫鏈法對EWMA控制圖參數優化算法進行了研究。

學術界和實際應用中常用平均運行鏈長（average run length，ARL）作為控制圖性能評價指標。運行鏈長（run length，RL）是對給定的質量水平、控制圖從開始應用到發出報警所抽取的樣本數，為隨機量，其分布狀況可以作為控制圖應用的決策依據。ARL是RL的期望值，理想控制圖的特點是：過程受控時，ARL值盡可能大；過程失控時，ARL值盡可能小。目前，常用的ARL計算方法有三種，即蒙特卡羅仿真法、積分法、馬爾可夫鏈法。基于馬爾可夫鏈法的EWMA控制圖ARL計算算法原理是：將EWMA控制圖的上下控制線之間的區間分成k（k為奇數）個子區間，將EWMA控制圖繪制的過程近似看成一個離散的馬爾可夫鏈（k的取值越大，該過程越近似于馬爾可夫鏈，則ARL可以用轉移概率矩陣表示。

本文在現有研究成果的基礎上，系統地研究了基于馬爾可夫鏈的EWMA控制圖參數優化方法，基于matlab進行仿真驗證，總結出具體的EWMA控制圖參數優化步驟，并基于J2EE平臺實現EWMA控制圖參數優化系統，進而與傳統的控制進行了比較研究。

1 EWMA控制圖

設X，N(μ0,σ02)其中μ0和σ02分別是過程處于受控狀態時的均值和方差。X1,X2,L,Xn（n為樣本容量），是相互獨立的隨機變量序列，其中Xi為第i個樣本值，則EWMA統計量為：

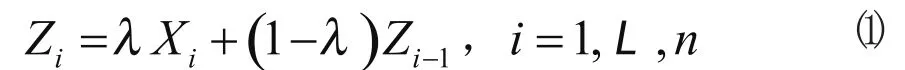
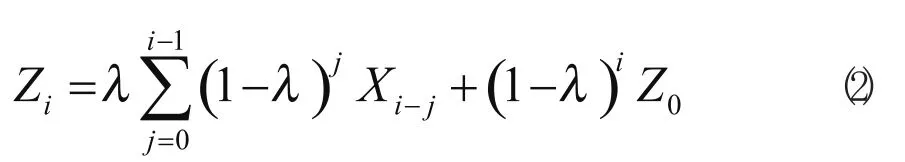
由式(2)可見，距離當前越遠的數據，權重越小，以指數形式遞減。

根據上述模型及六西格瑪原則，EWMA控制圖上、下控制限UCL和LCL，分別為[5]：

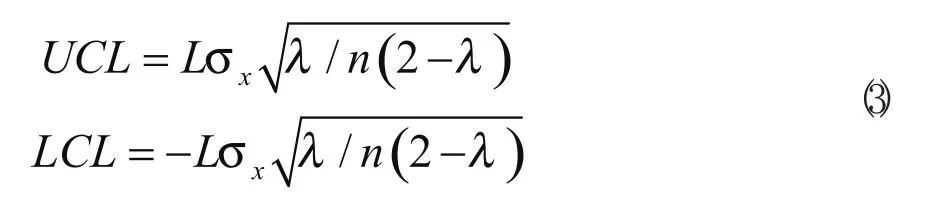
式中，n為樣本容量，λ為平滑系數，L為確定控制線的參數。由此可見，平滑系數λ及控制線參數L的選取是影響EWMA控制圖對小偏移控制的重點因素。

2 基于馬爾可夫鏈的ARL計算方法

圖1 馬爾可夫鏈狀態空間劃分示意圖

將EWMA控制圖繪制的過程近似看成一個離散的馬爾可夫鏈（k的取值越大，該過程越近似于馬爾可夫鏈），用Si(i=1,2,…,k)表示該馬爾可夫鏈的狀態，且設Si為子區間的中心點，則

統計量zi落在控制限之外的狀態表示為Sa，Si假設zi一旦超出控制限不會自動返回，則Sa為一個吸收態。這樣整個EWMA的監控過程就可以描述為帶有一個吸收壁的馬爾可夫鏈。該馬爾可夫鏈的一步轉移概率矩陣P可表示為

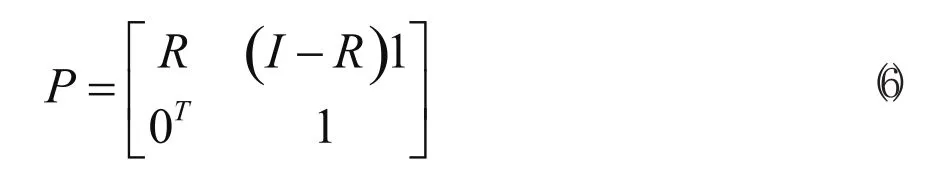
式中，R為k×k矩陣，表示從轉移狀態Si到轉移狀態Sj的概率Pij(i=1,2,…,k)。I為k×k單位矩陣，1為所有元素均為1的k×1列向量，0為所有元素均為0的k×1列向量。Pij可表示為：

由馬爾可夫鏈的定義，第i步轉移概率矩陣Pi可表示為

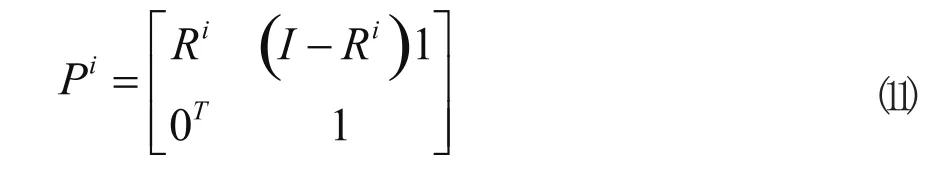
則鏈長PL=i的概率可以表示為

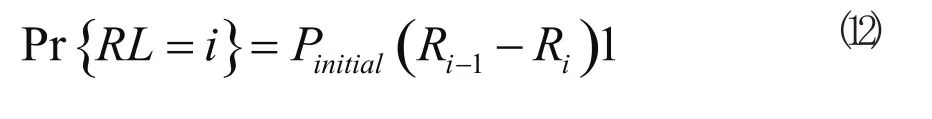
式中，Pinitial為初始狀態概率，為簡單起見設恒從中心點出發，因此

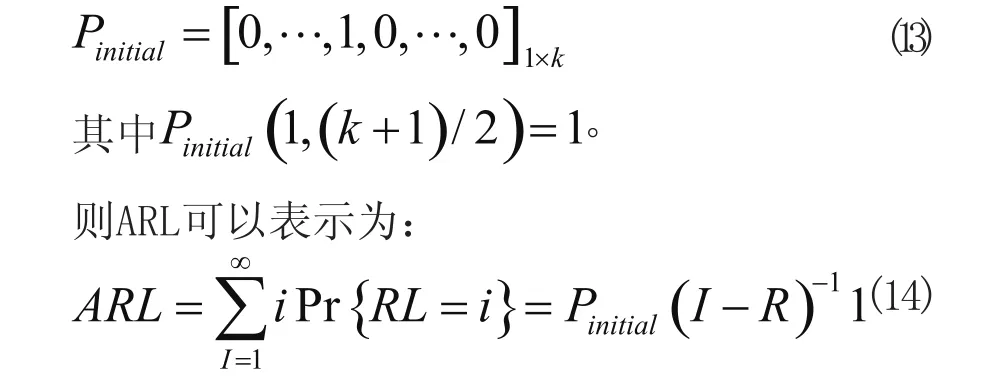
3 EWMA控制圖參數優化算法

基于上述計算EWMA控制圖ARL的數學模型，總結了EWMA控制圖參數優化算法。

EWMA控制圖參數優化算法流程如圖2所示：

圖2 EWMA控制圖參數優化算法流程

對于給定參數（λ,L）的EWMA檢驗方案來說，對過程的不同質量水平進行檢驗，其效果表現在它的ARL值。反之，對于一個具有不同質量水平的過程來說，其效果表現在給定受控平均運行鏈長值（ARL0）的情況下，能推導出適合的檢驗方案（λ,L）。

在進行EWMA控制圖的設計時，參數λ和L的選取至關重要。基于ARL的EWMA控制圖參數（λ,L）優化算的一般步驟如下：

1）先確定參數：置信度α、樣本容量n、欲控過程偏移量δ、標準差σ、馬爾可夫鏈區間劃分數k、控制線參數變化范圍LN，并計算出ARL0；

2）然后，計算滿足ARL0的幾組（λ,L）值對，擬合λ與L的回歸曲線；

3）擬合λ、L的回歸方程，以一定間隔取得（λ,L）值對；

4）根據（λ,L）值對及給定參數，計算取該參數時的ARL值；

5）計算ARL與λ的回歸方程，尋找ARLmin，從而得到優化參數（λ0，λ0）。

基于ARL的EWMA控制圖參數選取的方法是：在ARL0已定的前提下，即控制圖的置信度已知，選取參數（λ,L）使得ARL1越小越好。

4 基于matlab的EWMA控制圖參數優化

由前面基于馬爾可夫鏈的EWMA控制圖ARL的計算方法的研究可知，隨著區間劃分數k的增加，EWMA控制圖繪制過程越來越趨向于馬爾可夫鏈過程；為驗證算法的穩定性，取k從10到190，步長為4（δ=0.2,λ=0.2,L=2.7），基于matlab仿真ARL曲線如圖3所示。

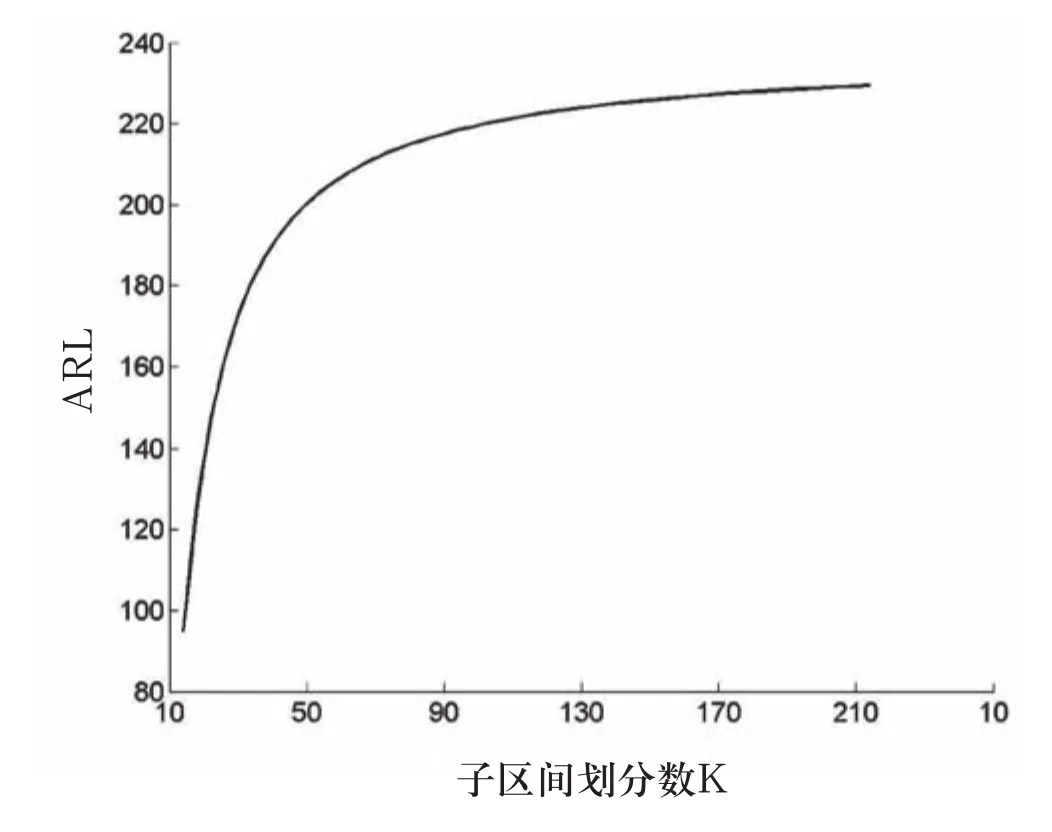
圖3 子區間劃分數對ARL計算結果的影響

隨著k的增加，ARL極限存在，由此可知，此過程可收斂。

下面研究EWMA控制圖參數對其過程控制的影響。

首先，研究不同控制線參數L(λ=0.23、k=50)下的EWMA控制圖操作特性（operation characteristic，OC）曲線，觀查控制線參數L對控制效果的影響，如圖4所示。

由曲線圖可見，L越大，ARL0越大，表示過程受控時誤判的概率越低。隨著偏移量δ增大，ARL呈下降趨勢，但L越大，ARL越大，也就意味著當過程失控（δ＞0）時，漏判的概率隨L的增大

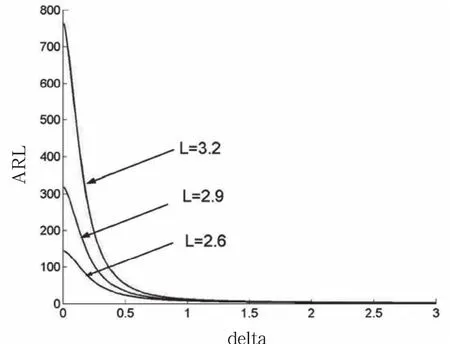
圖4 控制線參數 對EWMA控制圖OC曲線的影響

圖5 不同平滑系數λ下的EWMA控制圖OC曲線

由圖5可見，取不同平滑系數λ時， OC曲線存在交點δ?和δ??。δ=0時，λ越小，控制圖性能越優。0＜δ＜δ?之間，λ越大，控制圖性能越優。δ?＜δ＜δ??時，隨λ的減小控制圖性能變好；δ＞δ??時，控制圖的性能趨同。

5 EWMA控制圖參數優化實例

根據第4部分的結論，EWMA控制圖的性能與控制線參數L、平滑系數λ以及過程均值偏移量δ相關。顯然，需要根據過程均值波動的不同，選擇不同的參數。下面根據具體案例演示控制圖參數優化系統界面及優化參數選取過程。

在軸的車削加工過程當中，由于溫度升高以及磨損等原因導致刀具迸刀，因而軸的直徑發生了小偏移，假設偏移量為δ=1.0。為此，采用EWMA控制圖對軸的直徑進行過程監控，下面研究監控軸直徑的EWMA控制圖參數選取具體步驟：

1）在一定置信度（α=0.005）下，確定受控平均運行鏈長ARL0（200）、馬爾可夫鏈的子區間劃分數k(50)以及欲控偏移量δ（本例中為1.0）；

2）設δ=0，采用java計算程序，根據已知條件，計算出在不同λ下滿足ARL0的L，通常選取λ=0.1,0.2,L,0.9，見表1。然后采用回歸方法求出L與λ之間的關系式，如式15所示。

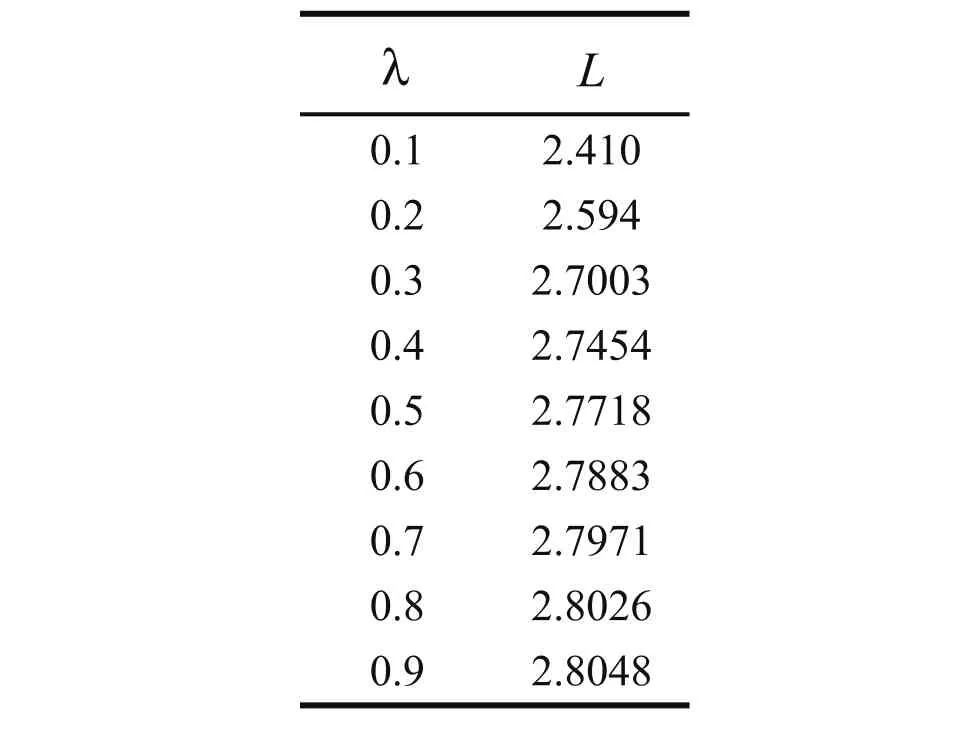
表1 幾組符合條件的（λ,L）值對計算結果

采用基于J2EE開發的控制圖參數優化系統演示λ與L的擬合曲線，得到λ與L之間的擬合曲線如圖6所示。

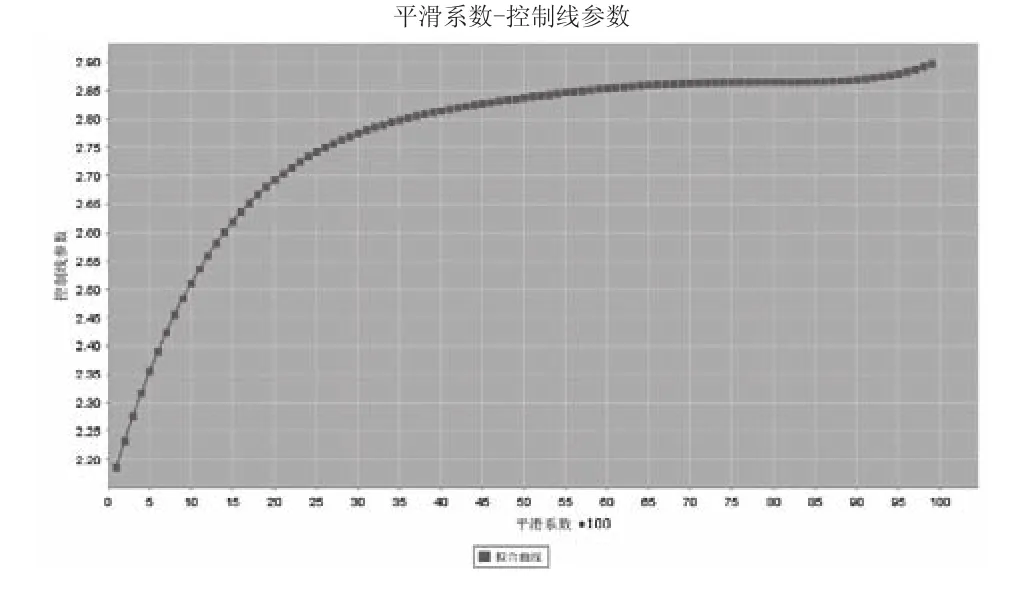
圖6 λ與L擬合曲線圖

3）在λ軸以0.01為間距，在λ、L的關系曲線上獲得（λ,L）值對。

4）計算取不同（λ,L）值對、過程偏移量δ=1.0時的ARL0值。的計算結果曲線如圖7所示。

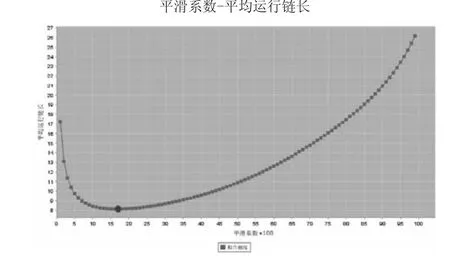
圖7 δ=1.0時ARL1.0與λ的關系曲線

5）從ARL1.0與λ的關系曲線，計算得到ARL1.0的最小值min(ARL1.0)=8.1341，以及此時對應的平滑系數λ0=0.17，在圖6上計算λ0=0.17所對應的控制線L0=0.17。此時的λ0=0.17、L0=2.6517即為該條件下EWMA控制圖的優化參數。對于優化后的EWMA控制圖，其在不同偏移量下的OC曲線如圖8所示。

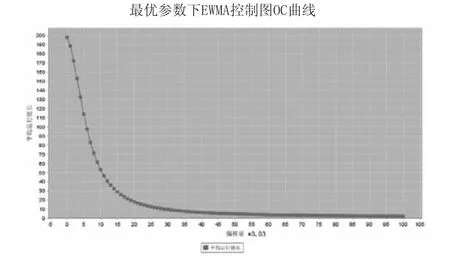
圖8 δ=1.0時最優參數下的OC曲線

在相同置信度α=0.9973及偏移量δ=0.17下，用matlab仿真休哈特控制圖和取不同參數的EWMA控制圖的ARL隨均值漂移的變化情況，表2比較了ARL計算結果：

由上述分析可見，當均值發生微小偏移δ＞0.5σ時，EWMA控制圖能比休哈特控制圖更即時地檢測出異常，因此對小偏移的控制更為靈敏，且在相同置信度α=0.9973下，參數取λ0=0.17、L0=2.8912時對偏移量δ=1.0最敏感，參數（λ0=0.17、L0=2.8912）即為置信度α=0.9973、偏移量δ=1.0下設計出的最優參數組合。

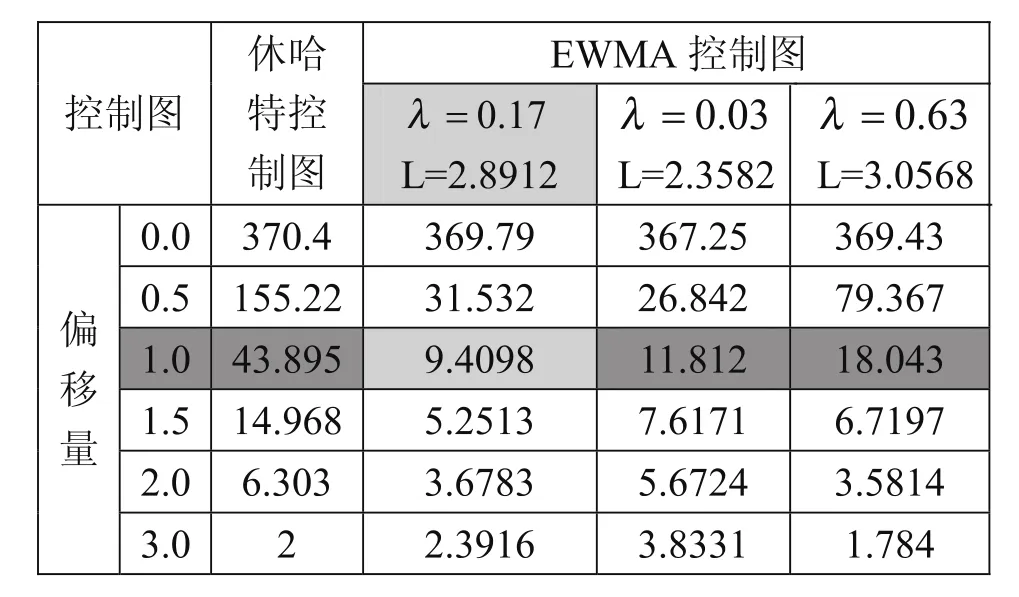
表2 休哈特控制圖與EWMA控制圖不同參數下的ARL

6 結論

本文研究監控小偏移過程的EWMA控制圖參數（λ、L）優化問題，基于馬爾可夫鏈法對EWMA控制圖的參數優化算法進行深入研究，并用matlab對EWMA控制圖參數優化算法進行仿真驗證，總結出在一定置信度及特定小偏移量下計算最優參數組合的一般步驟，通過比較驗證了優化參數的正確性，在上述研究的基礎上，基于J2EE平臺實現了控制圖參數優化系統界面。

[1]杜福洲.多元統計過程控制與診斷方法研究[D].北京:北京航空航天大學,2006,9.

[2]杜福洲,唐曉青,孫靜.MEWMA控制圖運行鏈長分析及實例研究[J].中國機械工程,2007,18(7):820-824.

[3]杜福洲,孫靜,唐曉青.基于馬爾可夫鏈的MCUSUM控制圖運行鏈長分析[J].清華大學學報,2007,47(2)169-172.

[4]Dogan A.Serel, Herbert Moskowitz Joint economic design of EWMA control charts for mean and variance,2008,157-168.

[5]何曙光,何楨,齊二石.基于馬爾可夫鏈模型的EWMA控制圖性能分析與優化[J].系統工程與電子術,2008,6(30):1127-1130.

[6]Su-Fen Yang,Yi-Ning Yu A Using VSI EWMA charts to monitor dependent process steps with incorrect adjustment 2009 442-454.

Parameter optimization and implementation for ewma control chart based on markov chain

BAI Shuang-mei, DU Fu-zhou

EWMA控制圖的性能取決于其參數的選取，學術界和工業界常采用平均運行鏈長作為控制圖性能評價指標，本文對基于馬爾可夫鏈的EWMA控制圖的參數（平滑系數 、控制線參數 )優化問題進行了深入的研究：給出了一種EWMA控制圖參數優化方法及一般步驟；采用matlab平臺對該算法進行研究并基于J2EE平臺實現EWMA控制圖參數優化系統界面，給出示例計算，并與傳統的控制圖進行了比較研究。

EWMA控制圖；小偏移過程；質量控制；matlab仿真；參數優化；系統實現

白雙梅 (1985－ )，女，內蒙人，碩士研究生，主要從事計算機集成制造、計算機輔助質量管理、過程管理等方面的研究。

TH166;021;0242;TP391

A

1009-0134(2010)06-0064-05

10.3969/j.issn.1009-0134.2010.06.22

2009-08-18

總裝預研項目；國防基礎科研項目