氣象衛星夜間微光云圖和紅外云圖的融合技術研究

劉凱,寇正

(解放軍理工大學 氣象學院，江蘇 南京211101)

氣象衛星云圖可分為可見光云圖和紅外云圖，前者只能在晝間得到，圖像中灰度取決于地表或云頂的反射率；后者在晝間、夜間均可獲得，圖像灰度取決于地表或云頂的溫度(即亮溫)。可見光云圖和紅外云圖是兩種具有互補性的圖像，單獨使用其中一種都有不足之處。夜間和晨昏時段只有紅外信息沒有可見光信息，使得大霧等災害性天氣的監測比白天難度要大。這種情形隨著美國國防氣象衛星（DMSP）的業務線掃描系統（OLS）的出現而得到改善，OLS傳感器可用于獲取夜間1/4月光和白天可見光云圖，以及晝夜紅外云圖。為了提高夜間云、霧的檢測和識別能力，考慮將微光云圖和紅外云圖進行融合。美國海軍研究室（NRL）曾開發了一種假彩色融合方法，能夠在融合后的圖像上比較容易地從色調上分辨出云和霧。假彩色融合法只是對微光云圖和紅外云圖融合進行了初步的研究。近年來，圖像融合技術特別是像素級圖像融合方法得到了迅速的發展，本文將多分辨率融合方法和多尺度幾何分析融合方法運用到兩種云圖的融合中，并用客觀評價指標對融合結果進行質量評價，對微光云圖和紅外云圖的融合進行了進一步的研究和分析。

1 圖像融合方法

目前主流的圖像融合方法包括多分辨率分析融合方法和多尺度幾何分析融合方法。

1.1 金字塔變換融合法

金字塔變換融合法是最早出現的多分辨率分析圖像融合方法。1983年，BURT P J和 ADELSON E H[1]提出了拉普拉斯金字塔變換；1985年，BURT P J和ADELSON E H[2]將拉普拉斯金字塔變換運用到圖像融合中，獲得了較好的融合結果；1989年TOET A[3]提出了低通比率金字塔變換融合方法；1992年BURT P J[4]提出了基于梯度金字塔的圖像融合算法。金字塔變換是一種冗余的圖像多分辨率分析方法，分解各層數據彼此相關。而且，除了梯度金字塔變換以外，其他的金字塔變換無方向性。

1.2 小波變換融合法

小波（Wavelet）變換融合法是另一類多分辨率分析圖像融合方法。1995年，LI H等[5]和CHIPMAN L J等[6]首先分別將小波變換引入到圖像融合領域中。小波變換同金字塔變換的不同在于，小波變換具有方向性，而且可以是非冗余的。

1.3 多尺度幾何分析融合法

上個世紀末， 以 RIDGELET[7]、CURVELET[8,9]、BANDLET[10]、CONTOURLET[11,12]、非 下 采 樣 CONTOURLET[13]為代表的多尺度幾何分析 (MGA)工具作為一種新的高維函數的最優表示方法相繼應運而生。從2005年開始，CHOI等、屈小波等、賈建等[14-16]相繼將MGA引入到圖像融合中。多尺度幾何分析融合法的基本思路同金字塔變換融合法和小波變換融合法相似，但其算法的計算復雜度較高。

2 圖像融合質量評價

本文采用平均互信息和Xydeas-Petrovic指標來評價融合圖像的質量。

2.1 平均互信息

源圖像A(或B)和融合圖像F之間的互信息(Mutual Information)定義如下：

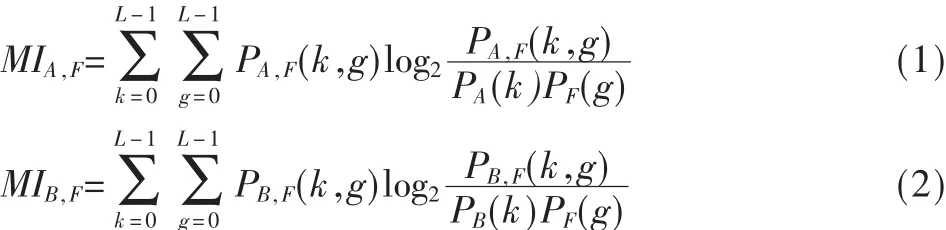
平均互信息[17,18]的定義為：

平均互信息越大，說明融合圖像從源圖像中提取的信息越多，融合的效果也越好。

2.2 Xydeas-Petrovic 指標[19,20]

QAB/F(m,n)的定義為：

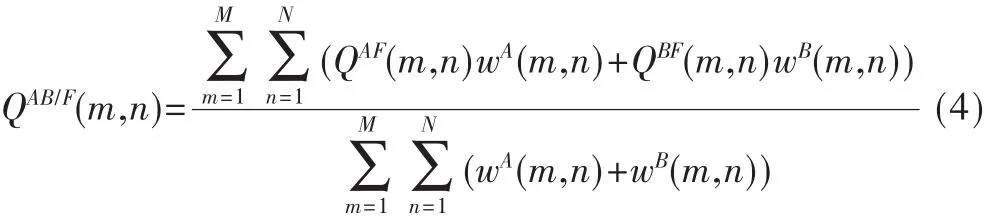
QAB/F(m,n)的值域范圍為[0,1]，值越大表示融合圖像保留了越多的源圖像邊緣信息，融合的效果越好。

3 融合實驗結果及分析

進行融合實驗的兩組源圖像分別截取自美國國防氣象衛星 (DMSP)2008年1月6日～7日的衛星云圖，該衛星云圖可從Internet上下載。微光云圖其成像被分成64個灰度級,紅外云圖其成像被分成256個灰度級。融合前把微光云圖的灰度級也拉伸到256個灰度級，大小均為 256×256。

分別用對比度金字塔(CON算法)、拉普拉斯金字塔(LAP算法)、離散小波變換(DWT算法)、非下采樣 Contourlet變換(NSCT 算法)、Bandlet變換(Bandlet算法)五 種方法對兩組實驗云圖進行融合，以上算法均采用低頻子帶系數取平均，高頻子帶系數模值取大的融合規則，分解級數均為4級。采用MI和QAB/F(m,n)指標分別對五種方法的融合圖像進行客觀評價。

圖1中,(a)、(b)為第一組微光和紅外源圖像，(c)～(g)分別為應用五種算法后的融合結果。第二組微光和紅外源圖像和融合結果圖略。表1、表2分別給出了兩組融合實驗的指標比較數據。

由圖 1(c)～(g)可以看到，五種融合算法都取得了良好的視覺效果。如表1所示，從MI指標看，NSCT算法最高，說明NSCT算法使融合圖像從源圖像中提取的信息最多；LAP算法次之，Bandlet算法最低。從指標QAB/F看，Bandlet算法最高，說明融合圖像中保留了源圖像中的邊緣信息最多；NSCT算法次之，而CON算法最低。綜合兩種指標，對第一組源圖像，NSCT算法和LAP算法的性能較其他三種算法好。對第二組源圖像，如表2所示，從MI指標看，LAP算法最高，NSCT算法次之，Bandlet算法最低。從指標QAB/F看，也是LAP算法最高,NSCT算法次之，Bandlet算法最低。綜合兩種指標，對第二組源圖像，LAP算法和NSCT算法的性能較之其他三種算法融合效果好。綜合以上兩組圖像融合實驗的結果，從MI和QAB/F看，LAP融合算法和NSCT融合算法的性能要優于其他三種算法，由于NSCT算法的計算復雜度較高，耗時較LAP算法多，而且圖像越大耗時越多，因此NSCT融合算法目前并不適合于實時處理，相對來說，LAP算法速度較快，適合于實時處理。

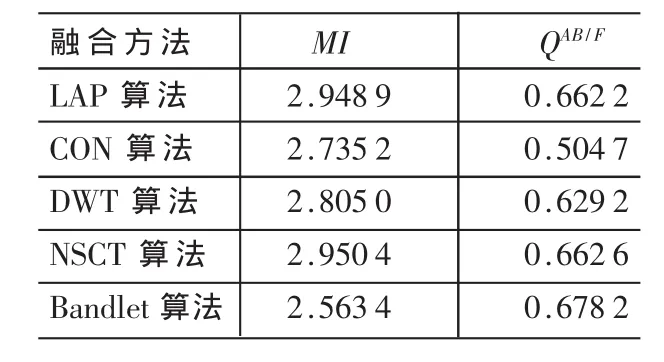
表1 微光云圖1、紅外云圖1的各種融合算法的性能比較

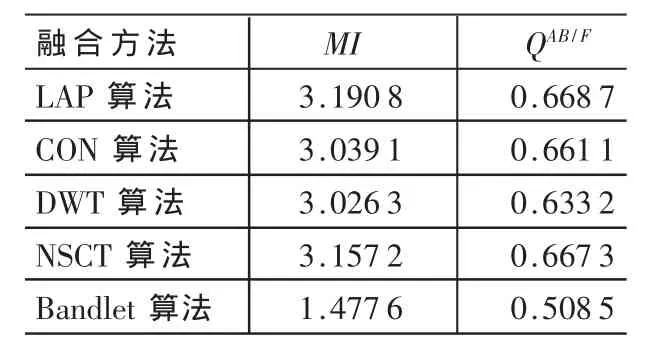
表2 微光云圖2、紅外云圖2的各種融合算法的性能比較

本文將多分辨率分析融合方法和多尺度幾何分析融合方法運用到DMSP氣象衛星夜間微光云圖和紅外云圖的融合中，從 MI和QAB/F指標看，拉普拉斯金字塔融合算法和非下采樣Contourlet融合算法的融合效果較其他方法優越。由于融合圖像的視覺效果比任一幅源圖像要好，因此，在融合圖像基礎上便于進行云類的識別和目標的檢測等進一步的工作，這也是后續要開展的研究工作。

[1]BURT P J,ADELSON E H.The laplacian pyramid as a compact image code[J].IEEE Transactions on Communications,1983,31(4):532-540.

[2]BURT P J,ADELSON E H.Merging images through pattern decomposition[C].Proceedings of SPIE on Application of Digital Image ProcessingⅧ,1985,575(3):173-181.

[3]TOET A.Image fusion by a ratio of low-pass pyramid[J].Patten Recognition Letters,1989,9(4):245-253.

[4]BURT P J.A gradient pyramid basis for pattern selective image fusion[J].Processings of the Society for Information Display Conference.San Jose:SID Press,1992:467-470.

[5]LI H,MANJUNATH B S,MITRA S K.Multisensor image fusion using the wavelet transform[J].Graphical Models and Image Processing,1995,27(3):235-244.

[6]CHIPMAN L J,ORR T M.Wavelets and images fusion[C].Proceedings of IEEE International Conference on Image Processing,Washington D.C.,1995:248-251.

[7]RIDGELETS E J C.Ridgelets:theory and applications[D].Ph.D.Thesis,Stanford University,USA,1998.

[8]CANDèS E J,DONOHO D L.Curvelets—a surprisingly effective nonadaptive representation for objects with edges.COHEN A,C.Rabut,L L SCHUMAKER(Eds.).Curves and surface fitting[M].Saint-Malo 1999,Vanderbilt University Press,Nashville,TN,1999.

[9]STARCK J L,CANDèS E J,DONOHO D L.The curvelet transform for image denoising[J].IEEE Transactions on Image Processing,2002,11(6):670-684.

[10]CANDèS E J,DEMANET L,DONOHO D L,et al.Fast discrete curvelet transforms[J].Multiscale Modeling&Simulation,2005,5(3):861-899.

[11]DO M N,VETTERLI M.Contourlets.G.V.Welland(Eds.),beyond wavelets[M].Academic Press,New York,2003.

[12]DO M N,VETTERLI M.The contourlet transform:an efficient directional multi-resolution image representation[J].IEEE Transactions on Image Processing,2005,14(12):2091-2106.

[13]CUNHA A L D,ZHOU J,DO M N.The nonsubsampled contourlet transform:Theory,design,and applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.

[14]CHOI M,KIM R Y,NAM M R,et al.Fusion of multispectral and panchromatic satellite images using the curvelet transform[J].IEEE Geoscience and Reomte Sensing Letters,2005,2(2):136-140.

[15]QU Xiao Bo,YAN Jing Wen,XIE Guo Fu,et al.A novel image fusion algorithm based on bandelet transform[J].Chinese Optics Letters,2007,5(10):569-572.

[16]賈建,焦李成,孫強.基于非下采樣Contourlet變換的多傳感器圖像融合[J].電子學報,2007,35(10):1934-1938.

[17]QU G,ZHANG D,YAN P.Medical image fusion by wavelet transform modulus maxima[J].Opt.Express,2001,9(4):184-190.

[18]QU G,ZHANG D,YAN P.Information measure for performance of image fusion[J].Electronics Letters,2002,38(7):313-315.

[19]XYDEAS C S,PETROVIC V.Objective image fusion performance measure[J].Electronics Letters,2000,36(4):308-309.