改進的六角網格系統上矩形窗口裁剪算法*

付文超,張傳林

(暨南大學 信息科學技術學院，廣東 廣州 510632)

裁剪是計算機圖形學中的一個重要內容，它能對圖形做出正確的判斷，去除不可見部分，選取可見信息提供給顯示系統進行顯示。目前研究的裁剪算法很多，矩形窗口的圖形裁剪算法更是使用最廣泛的一類算法，但這些算法都是基于方形網格系統提出和實現的。而早在20世紀60年代初,數學家們就已經提出了平面上點的最佳分布是按六角網格分布的[1]，這種分布就是用正六邊形來覆蓋整個平面，每個像素對應著一個正六邊形，將正六邊形的中心點作為網格點。相比于方形網格系統，六角網格系統具有更好的圖形圖像顯示特性[2-4]，因此基于六角網格顯示系統的圖形生成和處理算法的研究已成為了發展的必然。

本文給出了一種基于類直角坐標系的六角網格系統，并將其在方形網格顯示設備上進行模擬顯示，以作為六角網格系統上相關算法實現的模擬平臺。

總體來說，六角網格上的裁剪操作要比方形網格上麻煩，參考文獻[5]和參考文獻[6]中分別給出了一種基于六角網格的矩形窗口的線段和圓裁剪算法，參考文獻[7]給出了一種基于六角網格的圓形窗口的裁剪算法。這幾種算法都是基于傳統60°角六角網格系統提出的，算法處理比較復雜，導致六角網格系統優于方形網格系統的特性不再明顯。本文基于類直角坐標系的六角網格系統提出了一種改進的矩形窗口圖形裁剪算法，算法的復雜程度遠遠低于基于傳統60°角六角網格系統的相關算法。

1 兩種六角網格系統的比較

傳統60°角六角網格系統與方形網格系統的關系：傳統60°角六角網格系統上的任何一個點的坐標(x′,y′),都可以通過變換：

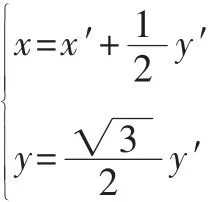
轉換成方形網格坐標(x,y)。

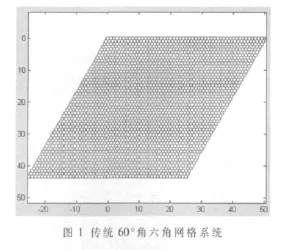
在方形網格顯示設備上模擬顯示傳統60°角六角網格系統，如圖1所示。

基于類直角坐標系的六角網格系統與方形網格系統的關系：基于類直角坐標系的六角網格系統上的任何一個點的坐標(x′,y′)，都可以通過變換：

轉換成方形網格坐標(x,y)，其中 r0=mod(y′,2)。

在方形網格顯示設備上模擬顯示基于類直角坐標系的六角網格系統，如圖2所示。

在傳統60°角六角網格系統上設矩形窗口裁剪算法要比在方形網格系統上麻煩,這是因為在傳統60°角六角網格系統上窗口的垂直邊界需要用一條斜線來表示，而不是用常數表達式來表示。

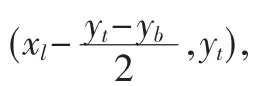
在基于類直角坐標系的六角網格系統上，設矩形窗口左下角點的坐標為(xl,yb)，右上角點的坐標為(xr,yt)，則矩形窗口的上邊界和下邊界表達式為 y=yt和y=yb。至于矩形窗口的左邊界和右邊界，可基于類直角坐標系的六角網格的排布特點（如圖3所示）來確定。

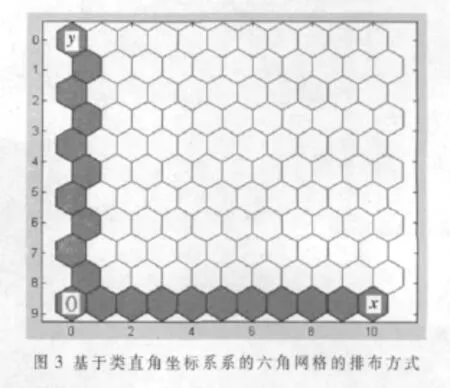
根據左下角的點(xl,yb)，可以知道矩形窗口左邊界的方程為x=xl，是一個常數表達式。但是，如果縱坐標yb為偶數，則左邊界x=xl直線上六角網格的排布就如圖4(a)所示；如果縱坐標 yb為奇數，則左邊界 x=xl直線上六角網格的排布就如圖4(b)所示。

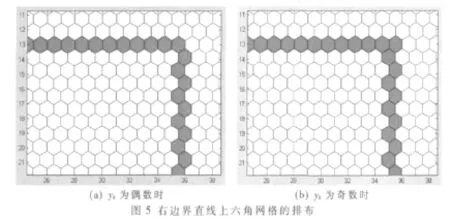
同樣地，根據右上角的點(xr,yt)，矩形窗口的右邊界的方程為x=xr，也是一個常數表達式。如果縱坐標 yt為偶數，則右邊界x=xr直線上六角網格的排布就如圖5(a)所示；如果縱坐標yt為奇數，則右邊界 x=xr直線上六角網格的排布就如圖5(b)所示。

綜上所述，可以在模擬實現的基于類直角坐標系的六角網格系統平臺上生成一個矩形窗口，如圖6所示。

2 基于類直角坐標系的六角網格上的矩形窗口裁剪算法

前面已經在六角網格系統模擬平臺生成了矩形窗口，下面討論基于類直角坐標系的六角網格上的矩形窗口裁剪算法，并給出一個在矩形窗口中裁剪圓的操作實例。

圓在基于類直角坐標系的六角網格系統中的方程為：

其中，(x0,y0)為圓心坐標，(x,y)和(x0,y0)均為六角網格系統中的坐標，R為圓的半徑。

圓與矩形窗口的位置關系，有包含、相離、相交三種。對于包含和相離的情況，裁剪操作很容易處理。對于相交的情況，必須求出交點坐標，并且把交點分為入點和出點兩類：入點即圓在該點處進入矩形窗口,出點即圓在該點處離開矩形窗口。由于圓是封閉曲線，因此如果圓在某一個點處進入矩形窗口，那么在它再次進入矩形窗口之前，中間必須有一個第三點使得圓先離開矩形窗口，即：在矩形窗口的邊界上，不會有相鄰的兩個入點；同理，在矩形窗口的邊界上，也不會有相鄰的兩個出點。

2.1 算法描述

在基于類直角坐標系的六角網格系統上使用矩形窗口裁剪圓曲線的流程是：先判斷圓與矩形窗口是否包含或者相離，如果是，則裁剪算法結束；否則，求出圓與矩形窗口邊界的交點，并進行裁剪操作。

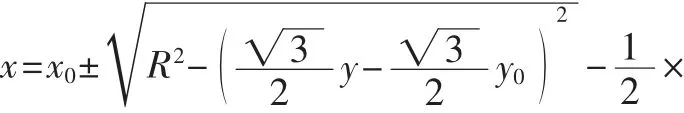
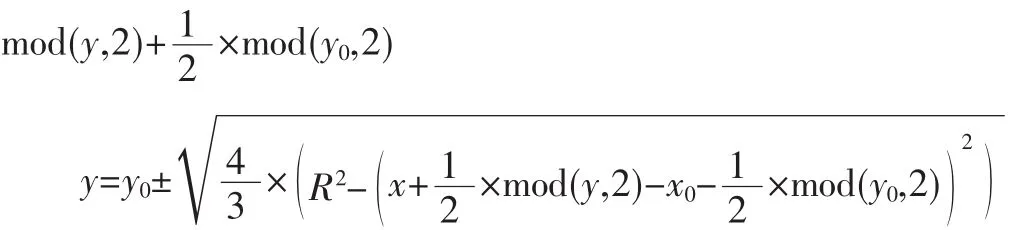
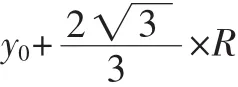
2.1.1 整個圓在矩形窗口內部(包含關系)

如果x坐標的最大值、最小值和y坐標的最大值、最小值滿足：

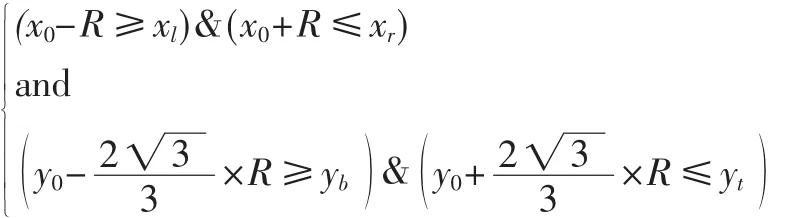
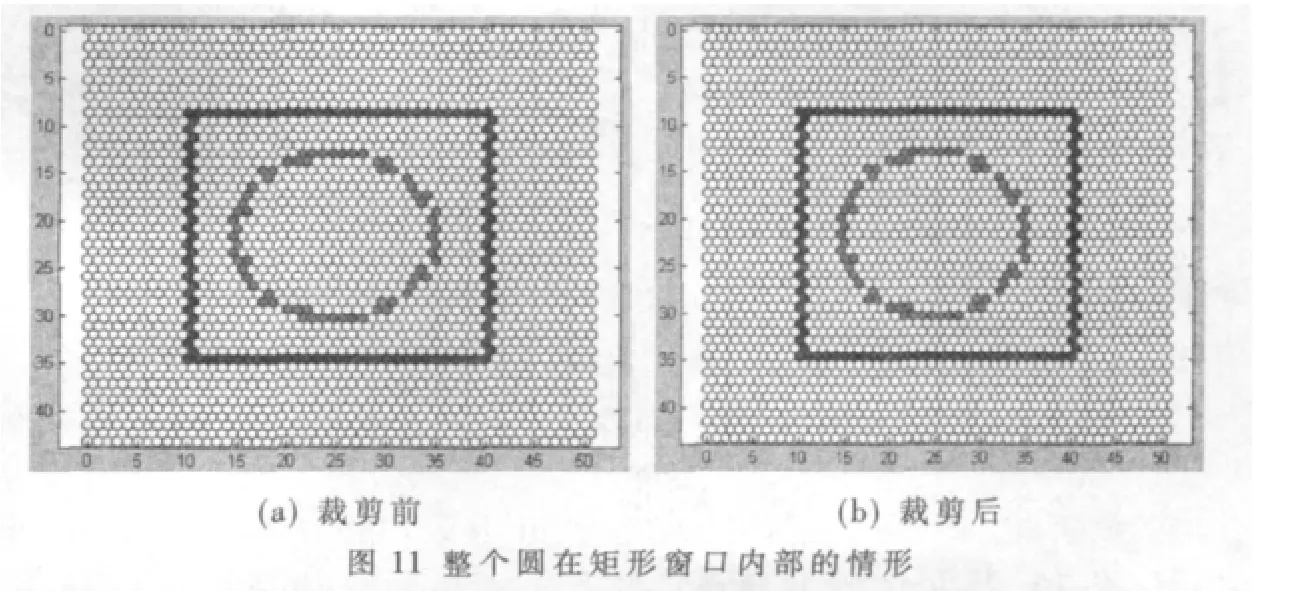
則整個圓在矩形窗口內部，如圖7所示，這種情況下不需要裁剪，整個圓在矩形窗口中都得到顯示。

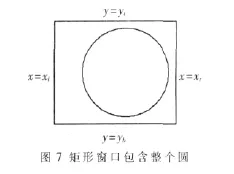
2.1.2 整個圓在矩形窗口外部（相離關系）

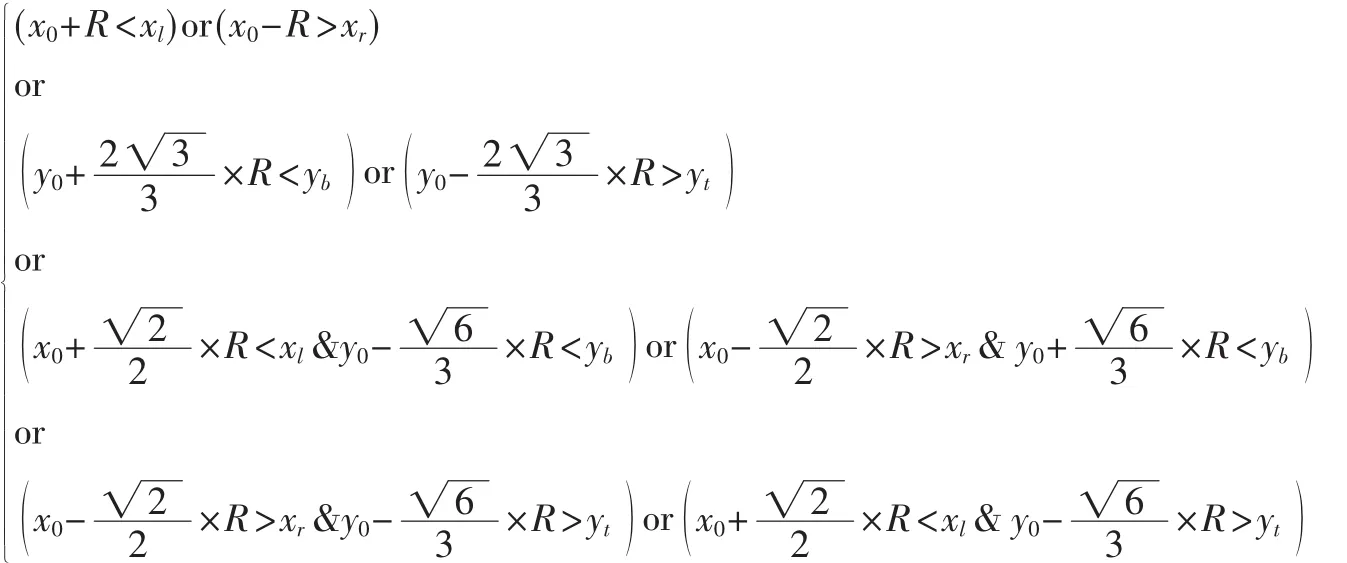
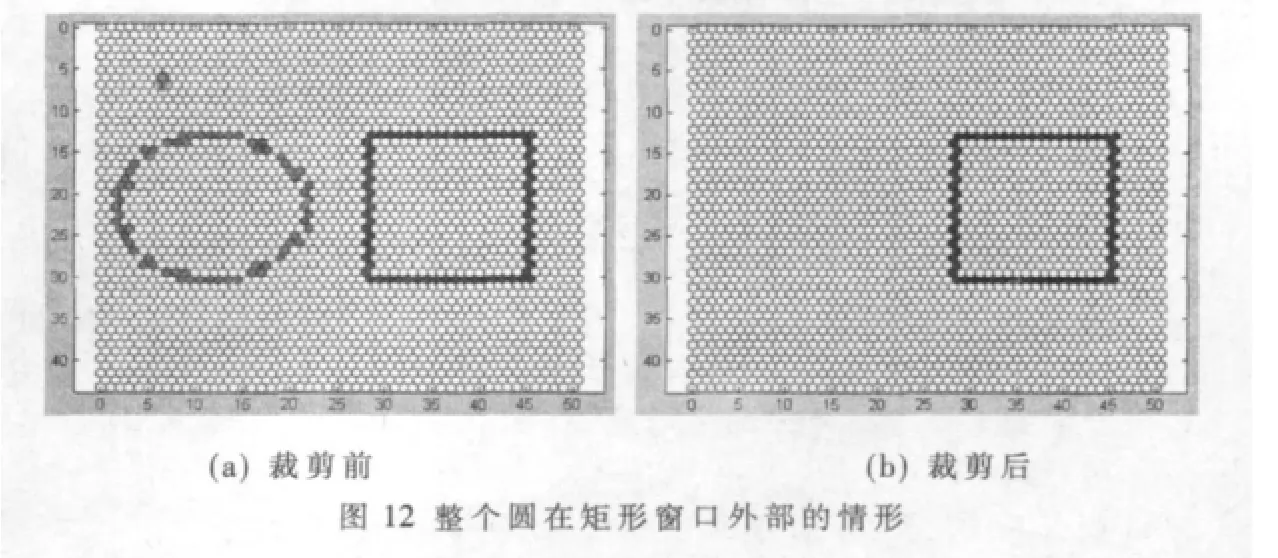
如果x坐標的最大值、最小值和y坐標的最大值、最小值滿足：則整個圓在矩形窗口外部，如圖8所示，這種情況下不需要裁剪，整個圓在矩形窗口中都沒有顯示。

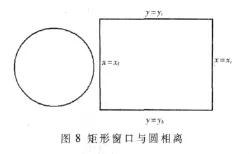
2.1.3 圓部分在矩形窗口內部,部分在矩形窗口外部（相交關系）

圓與矩形窗口相交是裁剪算法中最復雜的部分，這種情況下需要求出圓與矩形窗口的交點，并將窗口外的部分裁剪掉，顯示窗口內的部分。

將矩形邊界 方程 x=xl、x=xr、y=yb和 y=yt與 圓 的 方程聯立，求出所有交點坐標，寫入交點集合I。如果某個邊界與圓相切，只有一個交點，則該點不寫入交點集合。

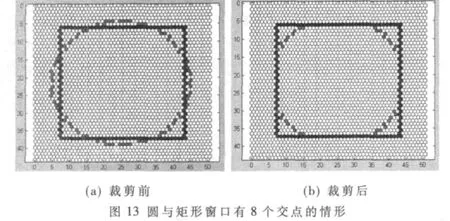
(1)矩形窗口與圓有 8個交點，如圖 9所示，記最下方交點中靠左的交點為I1，然后按照逆時針順序依次記其他交點為 I2,I3,…,I8。

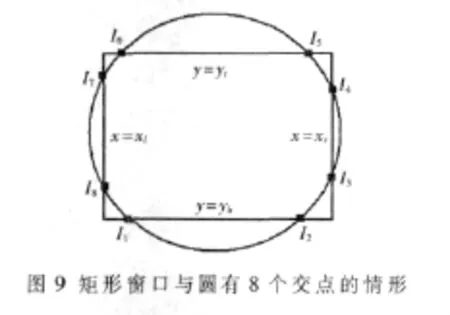
判斷I1是出點還是入點，方法是：如果I1在矩形窗口的下邊界上，則將I1=(x,yb)的橫坐標增加1并代入圓的方程，可求出相應的縱坐標y′有兩個，取圓弧上I1沿逆時針方向的下一個點 I1′=(x+1,y′)，如果 y′>yb，則 I1為入點，否則 I1為出點；如果I1在矩形窗口的右邊界上，則將I1=(xr,y)的縱坐標增加1并代入圓的方程，求出圓弧上I1沿逆時針方向的下一個點 I1′=(x′,y+1)，如果 x′xl，則 I1為入點，否則 I1為出點。

如果 I1為出點 ， 則圓弧 I2I3、I4I5、I6I7、I8I1位于窗口內部，將其余部分裁剪掉；如果I1為入點，則圓弧 I1I2、I3I4、I5I6、I7I8位于窗口內部， 將其余部分裁剪掉。

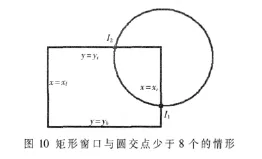
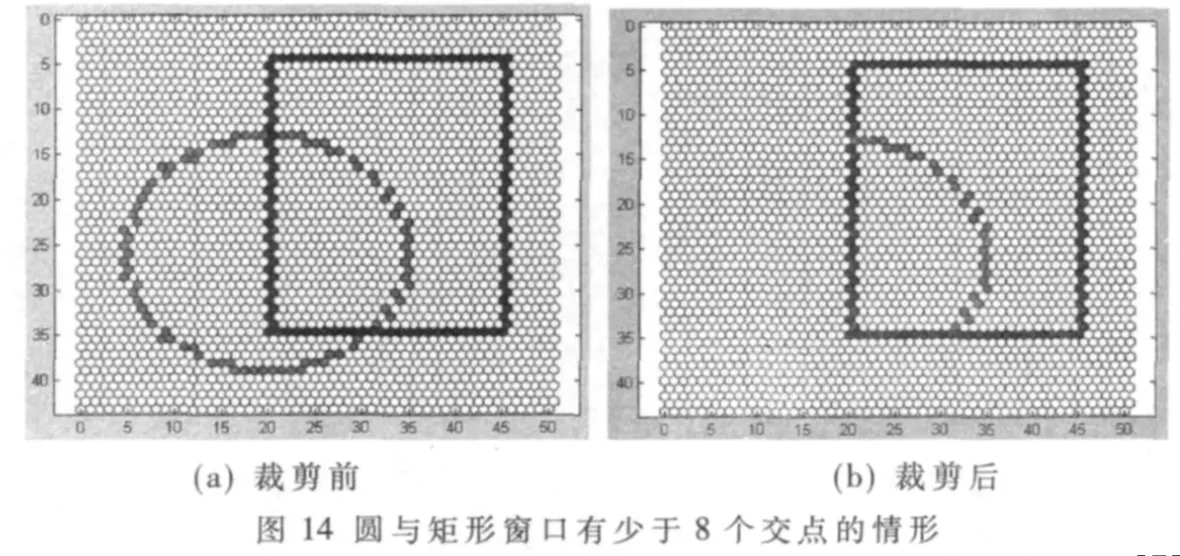
(2)矩形窗口與圓的交點少于8個，如圖10所示，仍然記最下方靠左的交點為I1，如果不存在這樣的I1，則按照逆時針順序，將遇到的第一個交點記為I1，其余交點順次標記。然后按照(1)中的步驟進行裁剪操作。

2.2 算法模擬實現

對本文提出的算法進行模擬,結果如圖11～圖14所示。

2.3 算法分析

由于六角網格系統的特殊性，一些在方形網格系統中比較簡單的公式在六角網格系統下就變得比較復雜，本文給出的基于類直角坐標系的六角網格系統的相關算法對該問題做了簡化，具有以下優點：

(1)矩形窗口的左右邊界也是一條簡單的垂直線，可以用常數表達式來表示，這樣就可以大大降低算法的計算量;

(2)算法處理速度快。本算法分三種情況來討論圓與矩形窗口的關系，前期先判斷圓與矩形窗口是否為包含或者相離的關系，通過簡單的比較運算來替代復雜的求交運算，減少了計算量;

(3)簡化了入點和出點的判斷。本算法利用封閉圖形的入點和出點在矩形窗口邊界上交互出現，只需判斷一個起始點為入點或出點，然后按照逆時針順序，根據入點和出點交互分布的原則依次判斷其他點是入點或出點。

在基于類直角坐標系的六角網格系統上，矩形窗口的邊界可以用常數表達式來表示，這大大簡化了六角網格系統上圖形裁剪算法的研究。由于這類六角網格系統上矩形窗口邊界表達式與方形網格系統上矩形窗口表達式形式一致，可以將方形網格系統上的其他圖形圖像處理算法直接或間接地移植到該類六角網格系統上。此外，本文給出的算法具有一定通用性，只需將圖形方程進行變化，即可適用于其他圖形圖像的矩形窗口裁剪。

[1]ROGERS C A.Packing covering[M].Cambridge：Cambridge University Press,1964.

[2]TIRUNELVELI G,GORDON R,PISTORIUS S.Comparison of square-pixel and hexagonal-pixel resolution in image processing[J].Proceedings of the 2002 IEEE Canadian Conference On Electrical&Computer Engineering.

[3]CONDAT L,Dimitri Van De Ville,BLU T.Hexagonal versus orthogonal lattices:a new comparison using approx-imation theory[J].ICIP:IEEE International Conference on Image Processing,2005,3:11-14.

[4]劉勇奎,鄒善舉.六角網格上的圖像算法及幾何量定義[J].計算機工程與設計,2000,21(1):61-64.

[5]趙慧杰,晏俊德,劉勇奎,等.六角網格單色顯示器及圖形算法研究[J].沈陽工業大學學報,1997,19(5):66-71.

[6]韓麗.基于六角網格的矩形窗口的圓裁剪算法[J].錦州師范學院學報(自然科學版),2003,24(4):64-66.

[7]孫長嵩,李麗潔,宋陽.一個基于六角網格的圓形窗口的裁剪算法[J].交通科技與經濟，2006,33(1):78-80.

[8]付文超,羅小華,張文爭,等.改進的六角網格下橢圓繪制算法[J].暨南大學學報(自然科學與醫學版).已錄用，待刊登.