一種基于級聯混沌系統的圖像加密算法

景運革，王彩霞

(運城學院 公共計算機教學部，山西 運城 044000)

目前混沌加密己成為密碼學研究的熱點之一，但已有的大部分混沌加密算法都是基于單個混沌系統的。事實表明，一些混沌映射可通過相空間重構的方法精確預測出來[1]。另外，由于計算機精度的限制，單混沌系統輸出的時間序列并不能達到理論上的完全隨機，而可通過多個混沌系統的級聯使這一缺陷得到改善[2]。為此，本文提出了一種基于多混沌系統級聯的圖像加密算法，理論分析與數值實驗均表明本算法能夠達到密碼學要求的混淆和擴散的目的，并能有效地預防差分攻擊。

1 混沌序列的生成

1.1 Logistic映射

Logistic映射由數學生態學家May于1976年提出，是非線性迭代方程和研究最廣泛的動力系統。Logistic映射的定義為：

當3.569 945 6<μ≤4時，Logistic映射工作處于混沌狀態，即由初始條件x0在Logistic映射的作用下所產生的序列{xk}是非周期、不收斂的，并對初始值非常敏感；當μ=4時，該映射是滿射，產生的混沌序列在區間(0，1)上具有遍歷性。由于Logistic映射具有與白噪聲相似的特性、簡單和初始值敏感性的特點，因此很多混沌圖像加密算法都是基于Logistic映射的。

1.2 時空混沌映射

時空混沌系統是一個空間上的擴展系統[3]，它展現了時間和空間上的混沌性。耦合映射格子(CML)通常被作為時空混沌系統使用，這種系統是具有離散時間、離散空間和連續狀態的動力系統。它由位于格子站點上的稱為局部映射的非線性映射組成，每個局部映射與其他局部映射以一定規則進行耦合連接。由于每個局部映射所固有的非線性動力特性及相互間耦合所產生的發散性，CML可以展現時空混沌性。所以采用不同的局部映射和耦合方法便可以構造出不同形式的CML[4]。本算法構造的二維CML為：

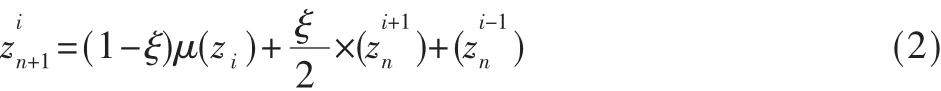
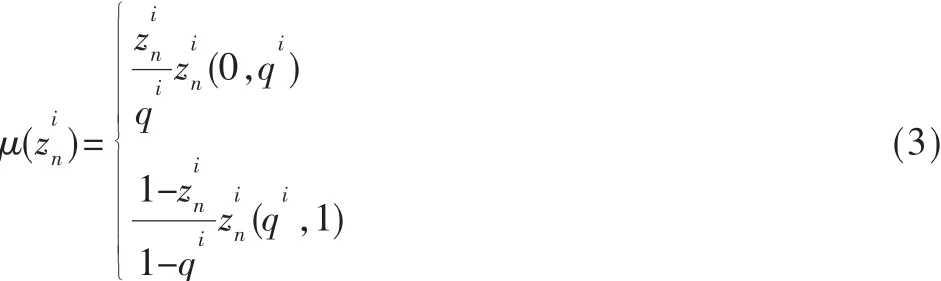
2 加密與解密的實現

本算法選用的混沌系統為時空混沌系統與一維Logistic映射。首先利用式(2)時空混沌系統產生隨機序列，然后將這個序列值分別作為式(1)的Logistic映射初始值，經過特定次數的迭代以后得到最后所需的混沌序列。這個特定次數是由上一個圖像像素加密后的結果決定的。

2.1 加密過程

假設待加密的數字圖像為z(M×N)。首先，將圖像 z中的像素值從左到右、從上到下進行橫向掃描，將掃描得到的像素值存儲到f(n)中。加密過程如下：

(2)對第i和i+1個像素加密時，首先將si作為式(1)的初值進行特定次數的迭代得到k。假設前兩個已加密的像素值分別為c(i-2)和c(i-1)，則求 k所需要的迭代次數為：

n=(c(i-2)+c(i-1))mod 25，其中當 n=0時，迭代 25次。K的二進制形式表示為∶

k=0b1(k)b2(k)……bi(k)……k∈(0，1)bi(k)∈{0，1}。第i個比特bi(x)可由下式得到：

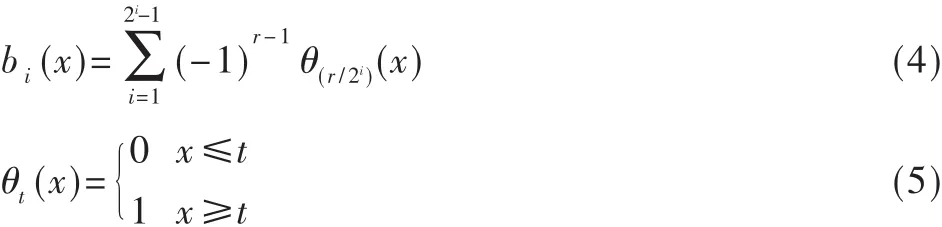
經計算可得到一個16位的比特序列，取前8位作為key1與第i個像素值進行“異或”操作得到密文c1(i)，取后8位作為key2與第i+1個像素值進行“異或”操作得到密文 c1(i+1)。

(3)對第1個和第2個像素值加密時，首先用由時空混沌系統式(2)產生的隨機序列s(1)作為初值進行迭代25次，將由步驟(2)得到的 key1、key2分別與對應的像素值進行“異或”操作得到密文c1(1)和c1(2)，然后按步驟(2)依次對圖像中的每個像素進行操作，最后可以得到圖像c1。

(4)對圖像c1按相反的方向從最后兩個像素開始按步驟(3)對像素值進行操作得到圖像c，即為加密后的密文圖像。

2.2 解密過程

解密過程與加密過程相反，即：將步驟(2)中提到的迭代的次數改為由密文圖像的前兩個像素值決定，再將步驟(3)與步驟(4)的順序顛倒過來，即可完成密文圖像的解密。

2.3 實驗結果

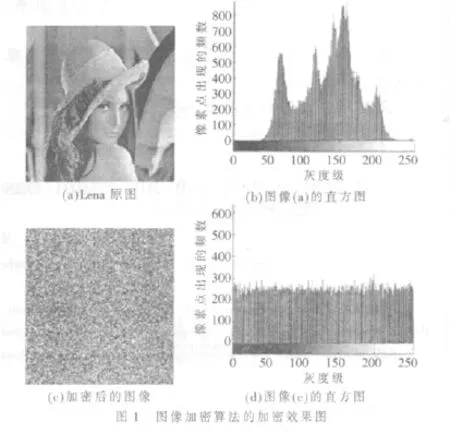
利用本文提出的算法，令Logistic映射的參數μ=4，ξ=0.99，時空混沌映射的初始值x=0.421 52、x=0.639 42、x=0.533 46、q1=0.327 54、q2=0.525 12 和 q3=0.832 14，對256×256的圖1(a)進行加密。圖1(c)即為加密后的結果。圖1(b)和圖1(d)分別是待加密圖像和已加密圖像的直方圖。

3 安全性分析

本算法有很高的安全性，具有更大的密鑰空間，且能夠抵御大部分常見的攻擊。

3.1 密鑰空間分析

3.2 密鑰敏感性的測試

圖2給出了密鑰敏感性的測試結果。其中圖2(a)是用正確密鑰 x=0.421 52、x=0.639 42、x=0.533 46、q1=0.327 54、q2=0.525 12和 q3=0.832 14進行解密后所得到的圖像；圖2(b)和圖2(c)分別是將密鑰中 x和 x改為0.421 53與0.639 42時解密后所得到的圖像。將圖2(b)和圖2(c)與圖2(a)進行比較，可見雖然密鑰僅發生了非常微小的改動，但是解密后的結果卻完全不同，這表明本算法對密鑰是敏感的。

3.3 統計分析

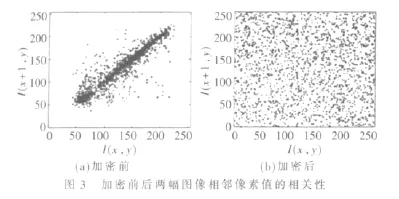
圖像中相鄰像素的相關性非常大，在加密過程中為了防御統計攻擊，必須使得相鄰像素間的相關性降低[5]。本文在待加密圖像和加密后的圖像中各隨機地選取了2 008對像素對，測試其水平方向、垂直方向、對角方向的像素相關性，并利用式(8)計算其相關系數：

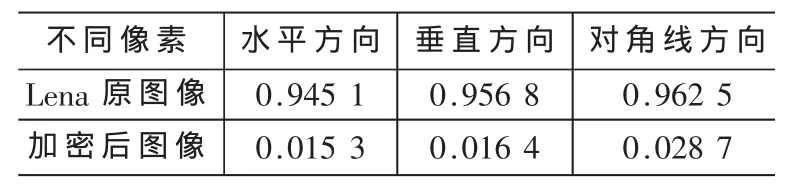
表1 相鄰像素值的相關系數rxy

3.4 差分攻擊分析

通過對待加密圖像做微小的改變，然后觀察該改變帶來的結果的方法，攻擊者可以獲得加密后圖像與原圖像之間的關聯。若某加密算法可使原圖像發生微小變化，使前后加密的結果變化很大，則該算法即可很好地預防差分攻擊。

像素數目改變率(NPCR)是指當待加密圖像改變一個像素時，加密后圖像像素數目的改變率。NPCR越大，表明加密算法對于待加密圖像變化越敏感，則該加密算法抵抗明文攻擊能力越強；平均強度變化率(UACI)是指待加密圖像和加密后圖像相應像素的平均強度的變化率，該指標越大，表示加密后圖像與待加密圖像比平均強度變化越大，則該加密算法抵抗差分攻擊能力越強。設兩幅加密后的圖像分別為c1和c2，則：

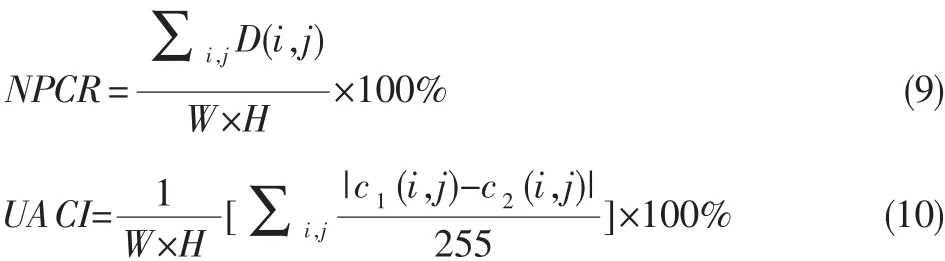
式 中，c1(i，j)、c2(i，j)分 別 表 示(i，j)處 的 像 素 灰 度 值，W 為圖像的寬度，H為圖像的高度。定義矩陣D(i，j)：若c1(i，j)=c2(i，j)，則 D(i，j)=0；否則 D(i，j)=1。

選取Lena原圖像圖1(a)作為測試對象，隨機選取其中某個像素點并改變它的像素值，然后用本算法對這兩幅差別微小的圖像加密，分析加密后圖像相同像素的比率。 經計算得到 NPCR=99.653 7%，UACI=37.682 5%，表明了即使將待加密的圖像做微小的改動，通過本算法加密后，也會得到明顯的差異。

3.5 信息熵攻擊

信息論是研究信息傳輸與信息壓縮的數學理論，最早由香農在1949年提出[6]。信息論中一個非常重要的概念就是信息熵，一個信息源m的信息熵：

式中，P(mi)表示信號mi出現的概率。對于給定的一個實際信息源很少能夠產生隨機的信息，所以通常它的熵值小于理想值。在對信息加密后，一般希望它的熵H(m)=8。若加密后的信息熵值小于8，則會威脅到所加密圖像的安全性。

利用本算法對圖2(a)進行加密得到圖2(c)，記錄圖2(c)中每一個不同像素值，并計算其出現的概率，最后可求出：

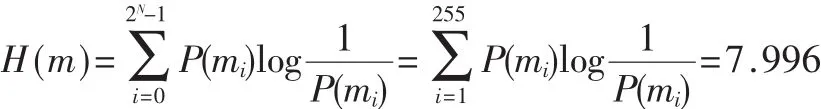
本文提出一種基于級聯混沌系統的圖像加密算法，采用由Logistic映射構成的一維CML作為時空混沌系統，然后將它的輸出序列作為Logistic由某一初始值經過特定次數的迭代后得到最終的密鑰序列。安全性分析表明，本算法的密鑰空間足夠大，使得暴力攻擊不可能。仿真實驗結果也表明，本算法具有較高的性能，在圖像加密和圖像傳輸中具有一定的潛在應用價值。

[1]ZHANG S， XIAO X C.Prediction of chaotic time series by using adaptive higherorder nonlinear fourier infrared filter[J].Acta Physica Sinica， 2000，49(7)∶1221-1227.

[2]KACHRIS C， BOURBAKIS N， DOLLAS A.A reconfig-urablelogic-based processorfortheSCAN imageand video encryption algorithm[J].International Journal of Parallel Programming， 2003，31(6)∶489-506.

[3]XIANG T， LIAO X F， TANG G P.A novel block cryptosystem based on iterating a chaoticmap[J].Physics Letters A， 2006，349(1)∶109-115.

[4]LI P， LI Z， WOLFGANG A.A stream based on a spatiotemporal chaotic system[J].Chaos，Solitons and Fractals，2007，32(5)∶1867-1786.

[5]孫偉.關于Arn01d變換的周期性 [J].北方工業大學學報，1999，11(1)：29-32.

[6]SHANNON C E.Communication theory of secrecy systems[J].Bell Syst Tech J， 1949，28：656-715.