基于誤判率的貝葉斯判別法在變形監測點穩定性分析中的應用
陳 超 張獻州
(西南交通大學土木工程學院, 四川成都 610031)
在變形監測過程中,監測點的相鄰兩期坐標之間存在差異,其包含了測量誤差和點位穩定性信息[1~2]。為了判斷這種差異究竟是測量誤差干擾還是點位變動引起的,本文采用基于誤判率的貝葉斯判別法對變形監測點的穩定性進行判別。
對于變形監測點的穩定性分析其實是一個分類問題,而且是一個二類分類問題,即穩定類(Ri)和非穩定類(Rj)
式中XΙ、XΠ分別為兩期坐標平差值,ΔX為坐標之差。Ri表示兩期坐標之差異是由測量誤差的干擾引起的,此時點位是穩定的;Rj表示兩期坐標之差異雖然存在測量誤差的干擾,但主要是由于點位自身的變動引起的,此時點位是非穩定的。
1 貝葉斯判別理論
在分類問題中,往往希望盡量減少分類的錯誤。從這樣的要求出發,利用概率論中的貝葉斯公式,建立基于誤判率的目標函數,得到分類規劃并對未知點進行判定的方法,稱之為貝葉斯判別法[3]。
類別的狀態是一個隨機變量,而某種狀態出現的概率是可以估計的。假設在m維空間中,對兩種類別(設類別為R1和R2)進行判定,識別前已知先驗概率P(R1)和P(R2),顯然有P(R1)+P(R2)=1。則合理的判別規則應為
若P(R1)>P(R2), 則做出屬于R1的判斷;若P(R1) 顯然,如果僅僅按照先驗概率判別就會把所有樣本點都判別為一類,而根本沒有達到把兩類樣點分開的目的。這是因為先驗概率提供的分類信息太少,為此還必須利用對樣本進行觀測和分析得到的信息,也就是構成樣本數據中的m維觀測量。在變形監測點的穩定性分析中,我們通常進行的是單點分析,這樣就有m=1。則觀測樣本X在Ri狀態下的類條件概率密度就為P(X|Ri),i=1,2。利用貝葉斯公式 (1) 得到的條件概率P(Ri|X)稱為狀態的后驗概率。因此,貝葉斯公式實質是通過觀察X把狀態的先驗概率轉化為后驗概率。則基于誤判率的貝葉斯判別規則為 若P(R1|X)>P(R2|X),則做出屬于R1的判斷;若P(R1|X) 設變形監測點穩定類和非穩定類的先驗概率分別為P(Ri)和P(Rj),則有P(Ri)+P(Rj)=1;兩類的類條件概率分別為P(X|Ri)和P(X|Rj)。由于測量誤差的存在,兩類的條件概率密度的分布在一般情況下總是存在著不同的重疊,在非重疊的區域內,樣本可以被正確的區分開;而在重疊的區域內,就不能正確的把樣本區分開,從而決定了錯誤率的大小。如圖1,圖中Pi(e)和Pj(e)分別為穩定類和非穩定類的錯誤率,θij為兩類條件概率密度分布的交點。 圖1 類概率密度分布及錯誤率示意 由于類概率距離Dij能直接反映類概率密度的分布情況,且又與誤判率P(e)密切相關,因此可成為類可分性的一種度量,作為變形監測點的穩定性判別的基準。 設在m維空間里,類概率密度P(X|Ri)的分布服從N(ξi,Σi),P(X|Rj)的分布服從N(ξj,Σj),且根據同精度觀測有Σi=Σj=Σ,則有 (2) (2)式中,ξi,ξj,Σ分別為均值矩陣和協方差陣,Dij稱為兩類之間的馬氏距離[5](是類概率距離的一種)。當樣本X的各維特征值之間相互獨立時,則有 (3) (4) (4)式中ξi,ξj分別為Ri類和Rj類的期望值,σ為兩類的方差(兩類方差相等)。 由(2)、(3)和(4)式可知,兩均值之間的距離越遠,且它們的分布越集中(方差越小),則兩類的類概率距離(Dij)就越大,反之,Dij越小。由此可知,在兩期觀測坐標及統計信息確定后,Dij的大小直接反映了兩期觀測值的可區分度。Dij越大,兩類就越容易區分,分類錯誤率越小;Dij越小,兩類越難區分,分類錯誤率就越大。 當類概率距離確定后,需要考慮該距離是否能區分兩期觀測值,即評價其優良性,在判別分析中采用誤判概率(P(e))來衡量。如果源于Ri(或者Rj)的樣品,取值落在Rj(或者Ri)中,那么按照貝葉斯判別規則就會把它誤判為Rj(或者Ri)的樣品,這種誤判的概率為 (5) 由圖1可知,分類誤判率P(e)為 P(e)=P(Ri)Pi(e)+P(Rj)Pj(e) (6) (6)式中P(Ri)和P(Rj)分別為變形監測點穩定類和非穩定類的先驗概率[6~9]。由于變形監測點的穩定性判別屬于二類分類問題,且假設兩類別出現的概率相等,即P(Ri)=P(Rj)=0.5。同時變形監測點服從方差相同的一維正態分布,即P(X|Ri)服從N(ξi,σ),P(X|Rj)服從N(ξj,σ),因此P(X|Ri)與P(X|Rj)密度分布將關于他們的交點θij(臨界值點)對稱,即θij為兩類空間取值范圍Ri與Rj的分界點。即可得 (7) (7)式中Dij為兩類之間的馬氏距離。則根據(5)式可進一步計算誤判率 (8) 由(6)、(7)和(8)可得 (9) 由上式可知,分類誤判率P(e)與類概率距離間存在反相關的關系。兩類之間的距離越大,誤判率越小;距離越小,誤判率越大。據此,我們可以通過設置適當的分類誤判率,由(9)式反向計算得到合理的判別距離基準,根據基準即可判別變形監測點的穩定性。 (2)計算DⅢ和P(e)。兩期觀測精度相同,且服從一維正態分布,則由上步算得的σ根據(4)式計算類概率距離DⅢ;并由(9)式計算誤判率P(e)。 (3)選擇判別基準D0。根據計算所得誤判率的大小,綜合工程的精度要求,合理的給定一個可接受的誤判率P0(e),由(9)式反向計算出判別的基準值D0。 (4)分類判別。根據表1的分類規劃進行變形監測點穩定性的判別。 表1 分類規劃 設有四點組成的二維(平面)網,按重心基準平差,兩期成果列于表2。 表2 平差坐標及其統計信息 傳統的做法是采用統計假設檢驗(t檢驗),以α=0.05為顯著性水平進行t檢驗,檢驗結果如表3[10]。 本文采用基于誤判率的貝葉斯判別法,根據計算所得的誤判率,并為了能與t檢驗法進行比較,綜合考慮,決定選取誤判率臨界值P0(e)=0.05進行判別。判別結果如表4。 表3 t檢驗法結果 注:√表示點位發生了顯著性位移。下同。 表4 基于誤判率的貝葉斯判別結果 (1)本文所述方法對于監測穩定性的判別結果與傳統t檢驗法所得的結果一致,驗證了該方法在變形分析中的可行性。 (2)在得出結論的同時還給出了誤判率,增強了判別結論的可靠性,與t檢驗法相比具有一定的優越性。 (3)本文方法可根據具體情況(如計算所得的誤判率大小),綜合考慮變形監測精度的要求,設置合理的誤判率臨界值,進而進行分類判別,有效克服了傳統t檢驗法中對于顯著性水平α選取的主觀性。 [1] 寇新建.變形分析的Bayes估計與檢驗[J].地殼形變與地震,1994,14(3):21-26 [2] 黃聲享,尹暉,蔣 征.變形監測數據處理[M].武漢:武漢大學出版社,2003 [3] 劉耀玲,焦利民.土地評價理論、方法與系統開發[M].北京:科學出版社,2008:132-134 [4] 高惠璇.應用多元統計分析[M].北京:北京大學出版社,2005:176-192 [5] 何 平.數理統計與多元統計[M].成都:西南交通大學出版社,2007:159-163 [6] 王科欣,徐 輝.基于最小錯誤率與最小風險的貝葉斯分類比較與研究[J].科技信息,2009(23) [7] 王義敏,安錦文.基于最小錯誤率的SAR圖象分割方法研究[J].計算機工程與應用,2006(16):80-82 [8] 包曉敏,汪亞明.基于最小錯誤率貝葉斯決策的蘋果圖像分割[J].農業工程學報,2006,22(5):122-124 [9] 沈 虹,汪劍鳴.基于貝葉斯最小錯誤率的一種新的指紋分割算法[J].微計算機信息,2006,22(1-1):208-210 [10] 陶本藻.自由網平差與變形分析[M].武漢:武漢測繪科技大學出版社,2000:111-114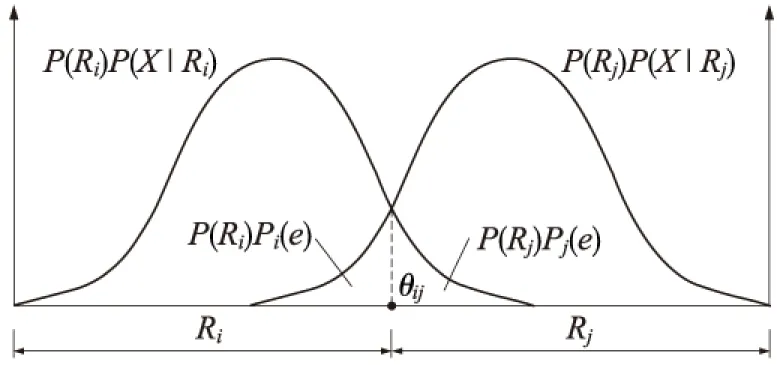
1.1 類概率距離(Dij)
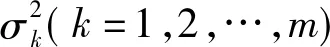
1.2 分類錯誤率(P(e))
2 分類判別步驟
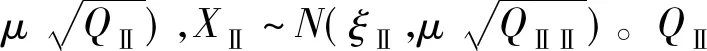
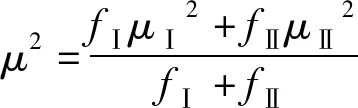

3 應用實例



4 結論

