神經網絡在PMV指標控制中的應用研究

李成利，黃存柱，常 軍

(青島科技大學 自動化與電子工程學院，山東 青島 266042)

隨著我國居民生活水平的持續提高，空調已進入千家萬戶。人們對空調的要求，已經不僅僅滿足于合適的溫度，而是要求房間整體環境具有舒適性，對空調控制理論提出了更高的要求。而我國能源匱乏且消耗巨大，故對空調的要求為舒適度和節能并重。

1 熱舒適性和PMV指標理論

根據人體工程學和微生物學的理論，人體在新陳代謝過程中產生熱量，人體散熱和體內新陳代謝產熱相平衡時，熱感覺良好，體溫保持在36.5℃左右，否則就覺得不舒服。在穩定狀態下，大多數人體的冷熱感覺可以由6大因素決定；(1)平均輻射溫度；(2)室內空氣溫度；(3)室內空氣相對濕度；(4)室內空氣流速；(5)人的活動量；(6)衣著[1]。平均輻射溫度可以用房間四周的平均表面溫度代表，人的活動量用人體的新陳代謝和機械功來表示，而衣著保溫程度則以服裝熱阻值和身體與穿衣的表面積比來作為指標。

熱舒適指標研究人體熱舒適感與熱濕環境構成因素之間的關系，將它們用固定的計算公式或計算方法相關聯。其中的平均預測投票PMV(Predicted Mean Vote)關聯了以上提到的6大因素與人體感覺之間的關系，是對人體熱感覺的近似模擬，Fanger教授進一步發展了熱舒適方程，并用公式表示一個可預測任何給定環境變量的參數組合所產生的熱感覺的指標并以此作為控制指標，這個指標就是PMV。

Fanger認為要滿足人最基本的3個條件，才能在某一熱環境中感到舒適。條件如下：(1)人與環境達到熱平衡，也就是人體蓄熱率S=0；(2)皮膚平均溫度應在與舒適相適應的水平；(3)人體排汗率應最佳，排汗率是新陳代謝的函數。綜合以上，可以獲得熱舒適方程的表達式[1]：

式中Icl為服裝的基本熱阻；fcl為服裝的面積系數；M為人體的新陳代謝率(W/m2)；η為人體的機械效率；V為空氣流速(m/s)；Pa為空氣水蒸氣壓力(kpa)；ta為空氣溫度(℃)。

PMV指標與6個因素關系式如下：

W為外部活動量，多數活動情況該值為零(W/m2)；Ia為衣服熱阻，Clo，1Clo=0.155(m2·℃)/W；tr為平均輻射溫度(℃)；hc為對流換熱系數 W/(m2·℃)；tcl為衣服的表面溫度(℃)[3]。

2 神經網絡在PMV值中的應用

綜前所述，PMV與各個參數之間的聯系復雜、計算繁瑣，尋找簡便方法十分困難。在此選用神經網絡的方法計算如下。

(1)輸入層與輸出層的設計

因PMV值與6個參數有關，故輸入層即為這6個參數，分別為平均輻射溫度、室內空氣溫度、濕度、室內空氣流速、人體活動量及衣著。對于輸出層，只有1個值PMV，所以選擇神經網絡的輸出層的神經元只有1個。故輸入層維數為6維，輸出層為1維。

(2)網絡隱層數的選擇

具有輸入層和至少1個隱含層加上1個線性輸出層的網絡，能夠逼近任何有理函數。如果增加隱層數，主要目的是進一步降低誤差、提高精度，但也使網絡復雜化，增加了網絡權值的訓練時間。在兼顧準確性與效率的前提下，最終確定此處為3層網絡。

(3)隱層神經元數的選擇

對于要建立的網絡，隨意選取神經元個數，根據實驗結果再作出調整，最終得到適合的每層神經元個數為6，21，1。

(4)初始權值的選取

PMV指標是個復雜的非線性關系，初始權值對于學習是否能夠收斂、訓練時間的長短以及是否達到局部最小關系很大。希望初始權值在輸入累加時，能使每個神經元的狀態值接近零，以保證在學習開始時，輸出不至落在平坦區內。因此，初始權值一般是隨機產生的，而且值要求比較小，如果一個神經元的輸入數為q，則初始權值可在[-2/q，2/q]之間。這樣就可以保證每個神經元從一開始就在它們激勵函數變換最大的地方進行學習。

(5)學習步長的選擇

學習步長選擇較小值，可使網絡總誤差函數E達到最小值。但如果步長過小，延長了網絡學習時間，將使得學習過程變得很慢；如果誤差函數有許多局部極小值時，會使網絡陷入局部最小值或進入平穩停滯狀態。學習步長如果選擇較大值，則使權值更新加快，同時加快了收斂速度；但學習步長如果選擇過大，有可能造成算法的不穩定，甚至無法收斂。所以根據PMV模型和此問題的性質，選擇初始步長為0.75[4]。

綜上所述，PMV指標的神經網絡預測模型如圖1所示。

圖1 PMV指標的神經網絡預測模型

3 BP神經網絡的構建和仿真

(1)網絡模型的構建與初始化

構建BP網絡模型的第1步是建立網絡對象并初始化，可用MATLAB神經網絡工具箱函數newff建立一個可訓練的單隱層BP網絡，其語法為：

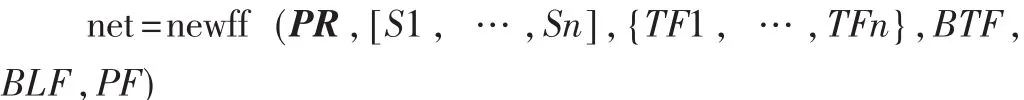
其中PR是 R×2的矩陣，用來定義 R個輸入向量的最小值和最大值；[S1，…，Sn]是包含每層神經元個數的數組，此處 BP網絡每層神經元的個數為 6，21，1，故S1=6，S2=21，S3=1； 網絡每層的加權函數為 dotprod；輸入函數為netsum；{TF1，…，TFn}用于指定各層神經元的傳遞函數，此處取“tansig”函數，它的作用是將神經元的輸入范圍(-∞，+∞)映射到(0，+1)；BTF 用于指定網絡的訓練函數的名稱，此處用trainlm；BLF為權值和閾值的學習函數，此處采用learngdm，該函數為帶動量項的BP學習規則；PF為網絡運行性能表征方式，此處采用最小誤差平方和可微函數mse[5]。

(2)網絡模型的訓練

在MATLAB神經網絡工具箱中有很多訓練BP神經網絡的函數，本課題采用trainlm函數，它的語法是[net，tr]=trainlm(net，Pd，TL)。 其中，net為初始化之后的網絡;tr為訓練過程中每一步長的網絡性能記錄;Pd為訓練網絡的輸入樣本；TL為訓練用的輸出樣本。

(3)網絡模型的仿真

BP網絡每次訓練結束后，都要驗證網絡性能。驗證時，使用sim函數模擬訓練后的網絡，其中新的網絡輸入pnew，網絡對象 net，返回網絡輸出anew，其語法為

[anew]=sim(net，pnew)

(4)程序實現及結果分析

其中A為平均輻射溫度、B為室內空氣溫度、C為室內空氣相對濕度、D為室內空氣流速、E為人體活動量、F為衣著情況[6]。程序數據參閱參考文獻[3]、參考文獻[4]。

根據以上程序，訓練結果為：

圖2 誤差收斂變化曲線

訓練的誤差收斂變化曲線如圖2所示，在訓練到36步時，網絡性能達到預期目標，可以計算出比較準確的數據。

根據以上訓練得到的神經網絡預測模型，可以應用到空調的控制系統中，根據PMV指標的變化情況調整空調的控制系數，使房間盡快達到最舒適的狀態。

[1]孫增圻，智能控制理論與技術[M].北京：清華大學出版社，廣西：廣西科學技術出版社，2004.

[2]申歡迎.基于PMV指標的舒適空調模糊控制系統仿真研究[D].西安：西安交通大學，2004.

[3]郭永吉.中央空調溫度控制系統研究[D].蘭州：蘭州理工大學，2008.

[4]劉謹.基于PMV指標的空調系統舒適控制研究 [D].長沙：湖南大學，2003.

[5]李翔.從復雜到有序：神經網絡智能控制理論新進展[M].上海：上海交通大學出版社，2006.

[6]董長虹，Matlab神經網絡與應用[M].北京：國防工業出版社，2005.