決策樹ID3算法研究及其優化

武獻宇 ，王建芬 ，謝金龍

(1.湖南現代物流職業技術學院，湖南 長沙 410131；2.長沙醫學院，湖南 長沙 410131)

分類是一種非常重要的數據挖掘方法，也是數據挖掘領域中被廣泛研究的課題。決策樹分類方法是一種重要的分類方法，它是以信息論為基礎對數據進行分類的一種數據挖掘方法。決策樹生成后成為一個類似流程圖的樹形結構，其中樹的每個內部結點代表一個屬性的測試，分枝代表測試結果，葉結點則代表一個類或類的分布，最終可生成一組規則。相對其他數據挖掘方法而言，決策樹分類方法因簡單、直觀、準確率高且應用價值高等優點在數據挖掘及數據分析中得到了廣泛應用。

1 決策樹分類過程

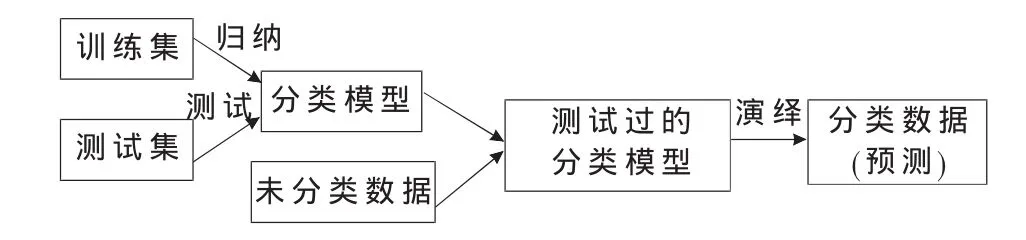
圖1 決策樹分類過程圖

決策樹的分類過程也就是決策樹分類模型(簡稱決策樹)的生成過程，如圖1所示。從圖中可知決策樹分類的建立過程與用決策樹分類模型進行預測的過程實際上是一種歸納-演繹過程。其中，由已分類數據得到決策樹分類模型的過程稱歸納過程，用決策樹分類模型對未分類數據進行分類的過程稱為演繹過程。需要強調的是：由訓練集得到分類模型必須經過測試集測試達到一定要求才能用于預測。

2 ID3算法

2.1 ID3算法的理論基礎

ID3算法的理論依據為：

設 E=F1×F2×…×Fn是 n 維有窮向量空間，Fj是有窮離散符號集，E 中的元素 e=＜V1，V2， …，Vn＞稱為例子，其中 Vj∈Fj，j=1，2，…，n。設 PE 和 NE 是 E 的兩個例子集，分別叫正例集和反例集。

假設向量空間E中的正例集PE和反例集NE的大小分別為p和n。ID3算法是基于如下兩種假設：

(1)向量空間E上的一棵正確決策樹對任意例子的分類概率同E中的正反例的概率一致。

(2)一棵決策樹對一例子做出正確類別判斷所需的信息量為:

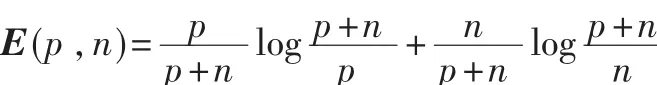
如果以屬性A作為決策樹的根，A具有V個值{V1，V2，V3，…，Vv}，它們將 E 分成 V 個子集{E1，E2，…，Ev}，假設 Ei中含有 pi個正例和 ni個反例，則子集Ei所需的期望信息是 E(pi，ni)，以屬性 A為根的期望熵為：

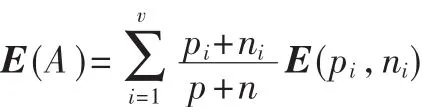
因此，以A為根的信息增益是：

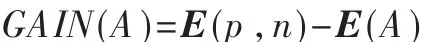
信息增益是不確定性的消除，也就是接收端所獲得的信息量。

2.2 ID3算法多值偏向性分析

首先，設A是某訓練樣本集的一個屬性，它的取值為 A1，A2，…，An，創建另外一個新屬性 A′，它與屬性 A唯一的區別：其中一個已知值 An分解為兩個值 A′n和A′n+1，其余值和A中的完全一樣，假設原來 n個值已經提供足夠的信息使分類正確進行，很明顯，則屬性A′相對于A沒有任何作用。但如果按照Qulnina的標準，屬性A′應當優先于屬性A選取。

綜上所知，把ID3算法分別作用在屬性A和屬性A′上，如果屬性選取標準在屬性A′上的取值恒大于在屬性A上的取值，則說明該算法在建樹過程中具有多值偏向；如果屬性選取標準在屬性A′上的取值與在屬性A上的取值沒有確定的大小關系，則說明該決策樹算法在建樹過程中不具有多值偏向性。

2.3 ID3算法的缺點

(1)ID3算法往往偏向于選擇取值較多的屬性，而在很多情況下取值較多的屬性并不總是最重要的屬性，即按照使熵值最小的原則被ID3算法列為應該首先判斷的屬性在現實情況中卻并不一定非常重要。例如:在銀行客戶分析中，姓名屬性取值多，卻不能從中得到任何信息。

(2)ID3算法不能處理具有連續值的屬性，也不能處理具有缺失數據的屬性。

(3)用互信息作為選擇屬性的標準存在一個假設，即訓練子集中的正、反例的比例應與實際問題領域中正、反例的比例一致。一般情況很難保證這兩者的比例一致，這樣計算訓練集的互信息就會存在偏差。

(4)在建造決策樹時，每個結點僅含一個屬性，是一種單變元的算法，致使生成的決策樹結點之間的相關性不夠強。雖然在一棵樹上連在一起，但聯系還是松散的。

(5)ID3算法雖然理論清晰，但計算比較復雜，在學習和訓練數據集的過程中機器內存占用率比較大，耗費資源。

決策樹ID3算法是一個很有實用價值的示例學習算法，它的基礎理論清晰，算法比較簡單，學習能力較強，適于處理大規模的學習問題，是數據挖掘和知識發現領域中的一個很好的范例，為后來各學者提出優化算法奠定了理論基礎。表1是一個經典的訓練集。

表1 天氣數據庫訓練數據集

由ID3算法遞歸建樹得到一棵決策樹如圖2所示。

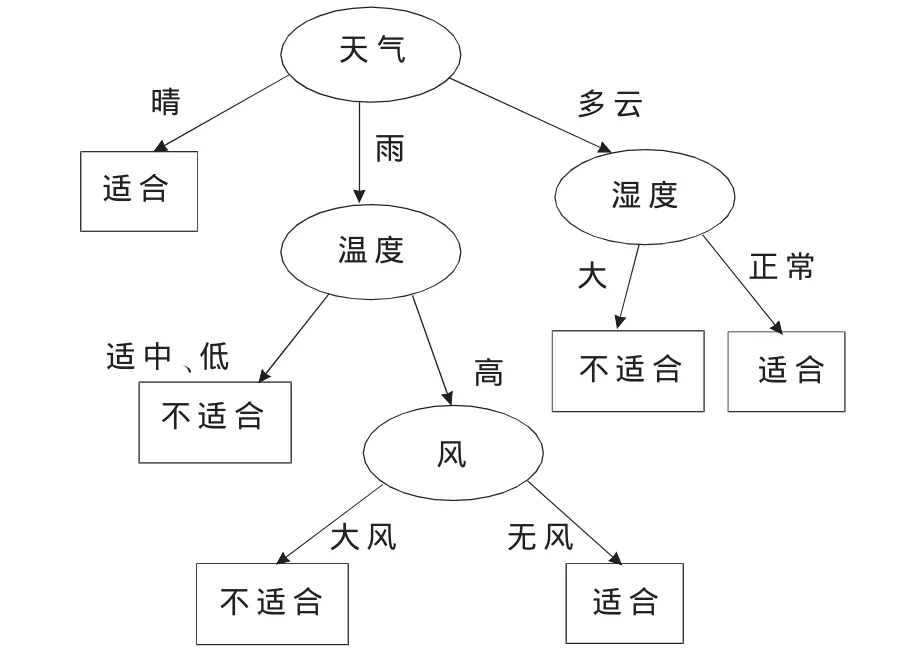
圖2 ID3算法所生成的決策樹

3 ID3算法優化的探討

ID3算法在選擇分裂屬性時，往往偏向于選擇取值較多的屬性，然而在很多情況下取值較多的屬性并不總是最重要的屬性，這會造成生成的決策樹的預測結果與實際偏離較大，針對這一弊端，本文提出以下改進思路：

(1)引入分支信息熵的概念。對于所有屬性，任取屬性A，計算A屬性的各分支子集的信息熵，在每個分支子集中找出最小信息熵，并計算其和，比較大小，選擇其最小值作為待選擇的最優屬性。

(2)引入屬性優先的概念。不同的屬性對于分類或決策有著不同的重要程度，這種重要程度可在輔助知識的基礎上事先加以假設，給每個屬性都賦予一個權值，其大小為(0，1)中的某個值。通過屬性優先法，降低非重要屬性的標注，提高重要屬性的標注。

4 實例分析

仍以表1為例，分別計算其H(A)的值。在此通過反復測試，天氣的屬性優先權值為0.95，風的屬性優先權值為0.35，其余兩個的屬性優先權值都為0。

(1)確定根結點

選取天氣屬性作為測試屬性，天氣為多云時，信息熵為：

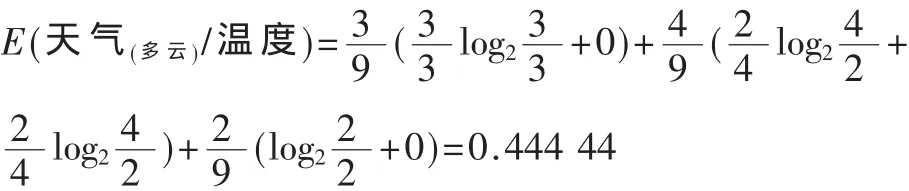
同理 E(天氣(多云)/濕度)=0，E(天氣(多云)/風)=0.972 77

從上面的計算可知，天氣為多云時的最小信息熵為0。

當天氣為晴時，由于此時對應的類別全部為適合打高爾夫球，所以信息熵都為0。

當天氣為雨時的信息熵為：

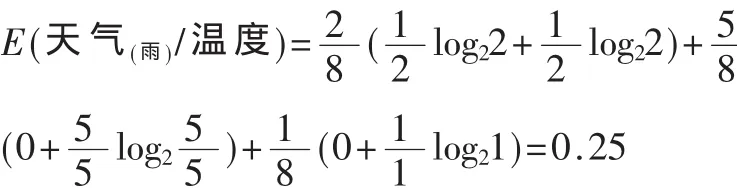
同 理 E(天 氣(雨)/濕 度)=0.451 21，E(天 氣(雨)/風 )=0.344 36

從上面的計算可知，天氣為雨時的最小信息熵為0.25。

同 理 H(溫 度)=1.083 83，H(濕 度)=1.068 7，H(風)=2.775 54

根據算法步驟(6)，選擇值H(A)為最小的作為候選屬性，所以此時應選擇濕度作為根結點。在24個訓練集中對濕度的2個取值進行分枝，2個分枝對應2個子集，分別為：

F1={1，2，3，4，5，6，7，13，14，21，22，24}(濕度為高對應)

F2={8，9，10，11，12，15，16，17，18，19，20，23}(濕度為正常對應)

(2)確定分支結點

計算F1分支子集：

H(溫度)=0.908 05，H(天氣)=0.95，H(風)=1.554 56

選擇H(A)值為最小的作為候選屬性，所以此時應選擇溫度作為濕度為大的下一級結點。在濕度為大的12個訓練集中對溫度的3個取值進行分枝，3個分枝對應3個子集，由于溫度為低的子集不存在，所以此時也只有2個子集，分別為：

F11={1，2，3，4，5}(濕度為大且溫度為高對應)

F12={6，7，13，14，21，22，24}(濕度為大且溫度為適中對應)

同理，對于F2分支子集：

H(溫度)=0.863 71，H(天氣)=1.250 8，H(風)=1.554 6

選擇H(A)值最小的作為候選屬性，所以此時應選擇溫度作為濕度為正常的下一級結點。在濕度為正常的12個訓練集中對溫度的3個取值進行分枝，3個分枝對應3個子集，分別為：

F21={8，10，23}(濕度為正常且溫度為高對應)

F22={17，18，19，20}(濕度為正常且溫度為適中對應)

F23={9，11，12，15，16}(濕度為正常且溫度為低對應)

繼續對 F11，F12，F21，F22，F23等分支子集采用此優化算法遞歸建樹，經過合并和簡化后得到的決策樹如圖3所示。

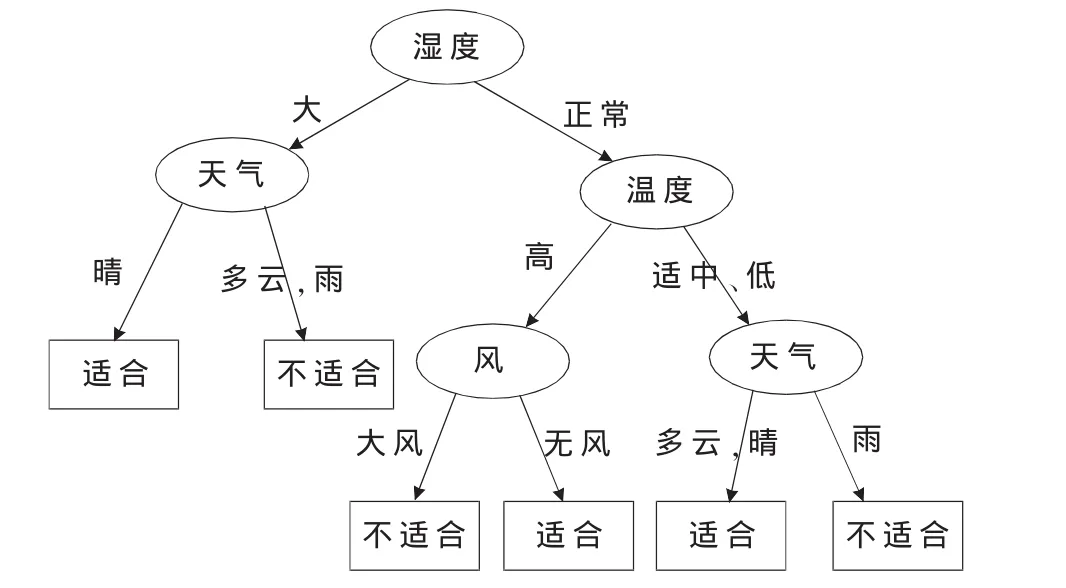
圖3 優化算法所生成的決策樹

通過比較ID3算法和本文所提出的組合優化算法所生成的決策樹可知，組合優化算法的改進為：

(1)從本實例所生成的決策樹的形態來看，改進后的算法生成的是一棵二叉樹，而ID3算法生成的是多叉樹，簡化了決策問題處理的復雜度。

(2)引入了分支信息熵和屬性優先的概念，用條件熵、分支信息熵與屬性優先三者相結合來選擇分裂屬性。從本實例來看，根結點選擇濕度而未選擇屬性值最多的天氣，所以本優化算法確實能克服傳統ID3算法的多值偏向性。

[1]安淑芝.數據倉庫與數據挖掘[M].北京：清華大學出版社，2005：104-107.

[2]史忠植.知識發現[M].北京：清華大學出版社，2002：23-37.

[3]徐潔磐.數據倉庫與決策支持系統[M].北京：科學出版社，2005：77-86.

[4]路紅梅.基于決策樹的經典算法綜述[J].宿州學院學報，2007(4)：91-95.

[5]韓慧.數據挖掘中決策樹算法的最新進展[J].計算機應用研究，2004(12)：5-8.

[6]KANTARDZIC M.Data mining concepts， models， methods，and algorithms[M].北京：清華大學出版社，2003：120-136.

[7]OLARU C，WEHENKEL L.A complete fuzzy decision tree technique[J].Fuzzy Sets and Systems， 2003，138(2)：221-254.

[8]AITKENHEAD M J.Aco-evolving decision tree classification method[J].Expert System with Application， 2008(34)：18-25.

[9]Norio Takeoka.Subjective probability over a subjective decision tree[J].Journal of Economic Theory，2007(136):536-571.