聯合生存概率準則下的最優再保險研究

李 凱

（中央財經大學 中國精算研究院，北京 100081）

0 引言

再保險精算研究中，最優再保險一直備受關注，最早由Pesonen[1]提出使原保險人風險的波動（即方差）達到最小作為最優準則，求得最優再保險的形式。Gajek[2],Kaluszka[3]則以原保險人方差最小作為最優準則，得到了最優再保險的統一形式。Young[4,5]研究了在Wang’s計算準則下，效用函數期望達到最大時的最優問題。以往大量的文獻僅僅考慮了原保險人的利益，而在再保險過程中，往往需要考慮再保險雙方的利益，因此，將原保險人和再保險人相結合進行研究亦頗具意義。曹云松[6]以原保險人和再保險人風險波動的凸組合作為目標函數，研究最優再保險的具體形式。在這些研究工作中，風險和效用函數常常作為衡量再保險合同優劣的標準。

原保險人與再保險人均希望獲得更多的保費，并承擔較低的風險，最優再保險策略應兼顧這兩方面的關系，更直觀的方法是以聯合生存函數作為優化準則，尋求聯合生存概率最大的再保險安排。本文主要研究在給定的時間段內，原保險人和再保險人的聯合生存概率問題，即雙方的理賠額均不超過各自收取的保費和初始余額之和的概率。假設發生總額為S的理賠時，原保險人承擔SI,再保險人承擔剩余部分SR=S-SI。我們將分別討論成數再保險（SR=（1-a）S）和停止損失再保險(SR=(S-M)+)。本文選擇期望值保費計算原理，即總保費P=(1+θ1)E(S)，再保險公司獲得保費 PR=(1+θR)E(SR), 而原保險人保留剩余部分P1=P-PR，其中θ1θR為附加因子，通常θ1≤θR。原保險人和再保險人的初始余額則分別為U1、UR,則雙方聯合生存概率為{Pr(SI≤PI+UI,SR≤PR+UR)},我們將重點研究在給定條件下，使得聯合生存概率最大的再保險策略，即

本文將通過推導和數值求解，分別給出成數再保險（比例）和停止損失再保險（非比例）的最優自留額。相對而言，成數再保險的最優解比較簡單且直觀，而停止損失再保險的結果則需要更多的推導。并通過具體的例子，計算停止損失再保險的最優自留額以及最大生存概率。

1 最優成數再保險

成數再保險是一種最簡單的分保方式，是指原保險人與再保險人在合同中約定保險金額的分割比例，將每一風險單位的保險金額，按照約定的比例在分出公司與分入公司之間進行分割的再保險方式。成數再保險的最大特征是“按比率”的再保險，即原保險人和再保險人保險金額的分攤、保險費的分攤、賠款的分攤都是按照合同規定的同一比例來進行的。

若理賠總額為S,那么原保險人承擔S1=aS,再保險人承擔SR=(1-a)S,其中0≤a≤1。雙方獲得的保費收入分別為：

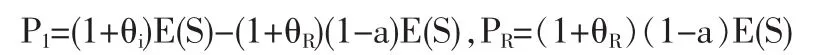
由于成數再保險的保費分攤也是按照一定比例進行的，因此θ1=θR,而為了從理論上探討最優再保險問題，并與全文內容保持一致，我們仍將θ1、θR看成兩個不同的參數，定理1給出了成數再保險的最優分保比例。

定理1 在成數再保險中，若原保險人和再保險人的初始余額則分別為U1、UR,保費計算均遵循期望值原理，則原保險人在準則(1)下的最優自留比例為

證明：在成數再保險中，賠款的分攤是按照合同規定的比例來進行的，故

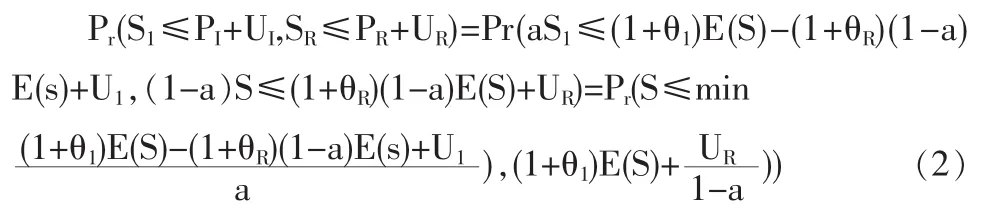
由于保險公司初始余額、附加因子以及理賠額的期望均已給定，因此聯合生存概率(2)是一個關于a的函數，不妨設為G(a)，下面我們分情況討論：

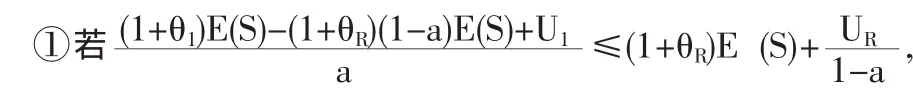
綜上所述，對于成數再保險而言，由于 θI=θR，故(2)式在a=UI/UI+UR處取得最大值，從而得到了原保險人的最優自留比例。

特別的，若UR=0,則a*=1,即完全不分保時，聯合生存概率最大。這個結果是顯而易見的，此時聯合生存函數

故不分保時達到最優。當然這是一種很特殊的情形，如果再保險人沒有初始余額，那么在分保后雙方的聯合生存概率總小于不分保時原保險人的生存概率。

成數再保險是一種最基本的再保險形式，手續簡單，且成本較低，雙方均按約定的比例分擔風險。若該比率與保險公司初始余額的比率保持一致，則聯合生存概率可達到最大值。如原保險人的初始余額較高，則應自留更高比例的風險；如再保險人的初始余額較高，則可分出更多的風險。

2 最優停止損失再保險

停止損失再保險是以損失為基礎來確定再保險當事人雙方的責任，自留額以內的損失完全由原保險人承擔，而再保險人對超過部分責任負責，即SR=(S-M)+。若損失金額（索賠額）x的密度函數為f(x)，其他條件不變，則再保險人獲得保費

若給定理賠額的分布，則原保險人和再保險人的聯合生存概率為M的函數G(M)，定理2給出了停止損失再保險的最優自留額及其存在的必要條件，符號和假定與前文均保持一致。

定理2 在停止損失再保險中，原保險人在準則(1)下的最優自留額M*需同時滿足如下條件：

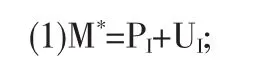
(2)損失金額S的分布函數在M*處的值F(M*

(3)聯合分布函數在M*處的值不小于不分保時原保險人的生存概率，即G(M*)≥Pr(S≤P+UI).

證明：原保險人和再保險人的聯合生存概率為M的函數，由停止損失再保險的性質，有：

G(M)=Pr(S1≤PI+UI,SR≤PR+UR)=Pr(S1≤PI+UI,SR≤PR+UR,SM)+Pr(SI≤PI+UI,SR≤PR+UR,S＞M)=Pr(SPI+UI,S≤M)+Pr(M≤PI+UI,S-M≤PR+UR,S＞M)

其中，UI、UR為正常數，PI、PR是關于 M 的函數， 對 PR求導可得：

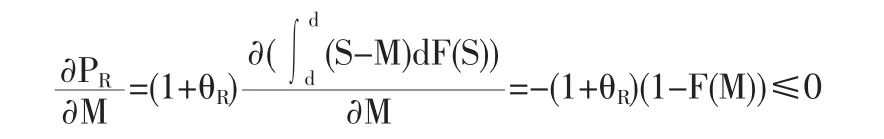
下面，我們分兩種情況討論：

①若M≥M*，則M≤PI+UI,

G(M)=Pr(S≤M)+Pr(M＜S≤PR+UR+M)=Pr(S≤PR+UR+M)

我們對函數G(M)求導：

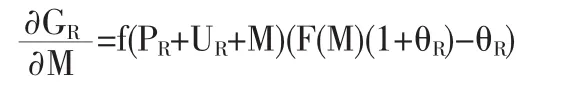
其中f、F分別是損失分布的密度函數和分布函數，F(M)==0，并設該點為。函數G(M)在左側遞減，在右側遞增。若M*≤，則G(M)在M=0處取得最大值，而這意味著全部風險分出，這是不合理的，最優自留額不存在。因此，最優解存在的一個必要條件是M*＞，即損失金額S的分布函數在M*處的值

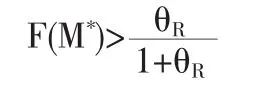
則函數G(M)在M*處取得最大值。

②若 M＞M*，則 M＞PI+UI,G(M)=Pr(S≤PI+UI),在此情形下，

綜上所述，停止損失再保險的最優自留額須滿足定理條件(1)、(2)，并且最優聯合生存概率不應小于不分保時原保險人的生存概率。

需要特別注意的是，函數G(M)在M*處是不連續的。左極限

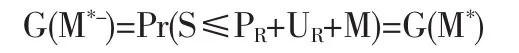
而右極限

顯然G(M*-)＞G(M*+)。事實上，在情形①中，風險自留額不超過原保險人保費與初始余額之和，我們只需考慮再保險人的生存概率；情形②中，風險自留額大于原保險人保費與初始余額之和，所以必須保證原保險人損失額小于保費與初始余額之和，而此時再保險人不需要理賠，必然生存。由于我們考慮的是雙方同時生存的概率，停止損失再保險合同又可以看成是一類分段函數，從而導致聯合生存概率函數在M*處不連續的。下面，我們通過兩個實際的例子，計算停止損失再保險的最優自留額。

3 實例分析

指數分布：若理賠額S服從期望為100的指數分布，即f(S=x)，μ=100。若停止損失再保險的自留額為M，則再保險人獲得保費

其中，附加因子θ1=0.1,θR=0.2，雙方的初始余額分別為UI=40，UR=10。 運用數值方法，可獲得方程 （1+θI）μ-(1+θR）μe=M 的根 M*≈110.1,此時顯然 。 聯合生存概率G(M*)=0.7980。如不分保，原保險人的生存概率為

F(S≤P+UI)=0.7769＜G(M*)

因此，M*≈110.1即為停止損失再保險在聯合生存概率準則下的最優自留額。

帕累托分布：若理賠額S服從期望為100的帕累托分布，即 f(S=x)，其中 k=400,α=5,其他條件同上，則再保險人獲得保費

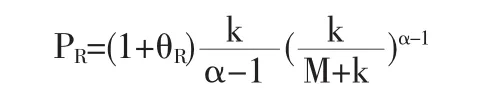
原保險人保留保費

F(S≤P+UI)=0.7956＜G(M*)

因此，M*≈110.4為帕累托分布下停止損失再保險的最優自留額。

4 小結

本文以原保險人和再保險人的聯合生存概率最大化為準則，分別探討了兩類常見的再保險形式：成數再保險和停止損失再保險的最優策略。研究結果表明，成數再保險的最優策略與雙方的初始余額直接相關。而停止損失再保險的最優策略須使得自留額與原保險人剩余保費相等，同時滿足最優解存在的必要條件。此外還通過具體實例驗證結論。基于該準則的最優再保險策略兼顧了再保險當事人雙方的利益，可為保險公司與再保險公司的決策提供有力依據。

[1]Pesonen,M.L.Optimal Reinsurances[J].Scandinavian Actuarial Journal,1984,84.

[2]Gajek,L.,Zagrodny,D.Insurer’s Optimal Reinsurance Strategies[J].Insurance:Mathematics and Economics,2000,27.

[3]Kaluszka,M.Optimal Reinsurance Under Mean 2 Variance Premium Principles[J].Insurance:Mathematics and Economics,2001,28.

[4]Young,V.R.Optimal Insurance under Wang’s Premium Principle[J].Insurance:Mathematics and Economics,1999,25.

[5]Young,V.R.Discussion of Christofides’Conjecture Regarding Wang’s Premium Principle[J].ASTIN Bulletin,1999,29(2).

[6]曹云松.最優再保險的研究[D].浙江大學碩士論文，2006.