一種新的艦船電子設備失效分布的探討

劉 會 李 蕾

中國艦船研究設計中心，湖北武漢 430064

一種新的艦船電子設備失效分布的探討

劉 會 李 蕾

中國艦船研究設計中心，湖北武漢 430064

隨著現代艦船電子技術的發展設備技術性能和結構要求提高，可靠性問題愈顯突出。根據電子設備的現實使用情況，在其壽命方差線性變化的假設下，推導一種新的電子設備失效分布；進一步研究該分布密度函數中的參數特性，以及在完整數據情況下參數的負指數矩估計；推導新失效分布下電子設備的可靠性指標。實證分析表明選取的該電子設備失效率隨時間的增長而增大，故符合推導的新分布的情況，分析結果與實際情況基本符合，說明推導的新分布及相應的密度函數性質、參數估計方法以及可靠性指數的計算等是切實可行的。

可靠性；新失效分布；負指數矩；估計

1 引 言

隨著電子技術的發展，現代艦船對電子設備也提出了更高的要求。由于設備技術性能和結構要求等方面的提高，可靠性問題愈顯突出。如果沒有可靠性保證，高性能指標是沒有任何意義的，特別對現代軍艦來說，可靠性就是戰斗力，就是生命，關系到戰爭的勝負。從部件、元器件的角度來講，電子元器件的可靠性水平決定了設備的可靠性程度。從軍艦的設計建造來講，可靠性貫穿于設計、生產、管理中［1～3］。

合理分析和評價電子設備的可靠性，科學合理地認識電子設備失效情況，對于通信導航、敵我識別等系統的可靠性有重大意義。可靠性屬于質量管理的范疇，是產品質量的時間函數。從基本概念上講，可靠性指標與質量的性能指標所強調的內容是不同的，可靠性的基本概念與時間有關，它是產品故障或壽命特征的數學模型化［4-5］。

2 電子設備失效新分布

在可靠性工程中，最常見的壽命分布函數有指數分布、威布爾分布、對數正態分布和正態分布。目前，絕大多數關于電子設備的可靠性分析中，都假定電子設備的失效分布服從指數分布［6］。從電子設備及許多電子元器件的失效機理來看，隨著時間的足夠長，失效率趨近于一個穩定值，其基本特征可以用指數函數的曲線相比擬，即服從指數分布［7-8］。然而，指數分布在傳統可靠性分析中廣泛應用的壽命分布形式的適用范圍，實際上是很有限的，它只適用于失效率為常數的情形。

正常情況下，失效率隨著時間的增長是逐漸增大的，下面從電子設備的現實使用情況出發，推導電子設備的失效分布，因為失效即意味著壽命結束，故失效分布也可稱為 “電子設備的壽命分布”［9-10］。

考慮電子設備壽命波動的方差，由于考慮系統的可靠性，方差不能超過最大值Kmax。當K＞Kmax時，該電子設備將不再被使用。假定在一小段時間內隨設備使用時間增加而增加，一般假設為線性變化：

式中，r表示變化率，受系統內外環境、使用人員能力等眾多獨立微小因素的影響，因此可以認為r為服從類似于均值為，方差為σ2的正態分布隨機變量。由于有r＞0的限制，可視該分布為截尾正態分布，密度函數不妨設為：

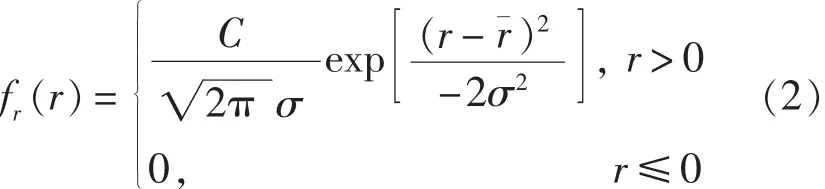
式中，常數C可由密度函數積分為1的性質計算出來：

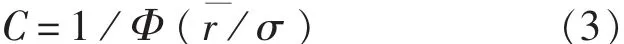
式中，Φ為標準正態的分布函數。正態分布是自然界中最常見的分布，這里由于r＞0，故假定其分布為截尾正態分布是非常合理的。

設一個設備的壽命時間為T，則

也是隨機變量。由概率論里隨機變量函數的分布密度的推導，可以求得T的密度函數

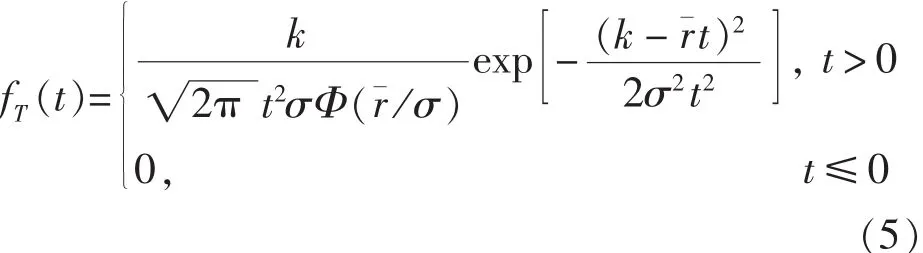
式中，k＝Kmax。T的分布函數為：

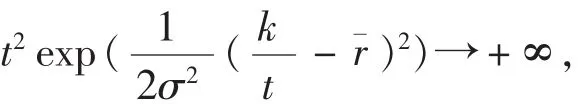
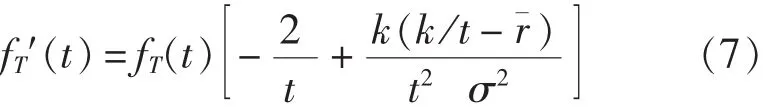
方程 f′（t） ＝0 的解為：

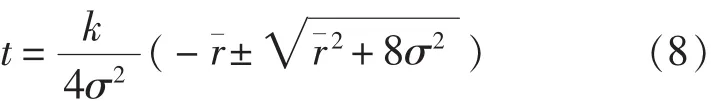
當 t＞0時， 方程 fT′（t）＝0有唯一解， 此時 fT（t）有唯一峰值，即該密度函數圖像是單峰的。它的左極限是原點，右側水平漸近線是t軸。它的眾數由上式（8）所決定。這個分布不妨稱其為“電子設備失效新分布”。

這里設定壽命方差隨時間線性變化。線性變化是一種較簡單的函數形式，只要壽命方差與時間之間存在單調函數關系，都可以依據本文的推導方法進行失效率分布的推導。

3 完全樣本的參數估計

在研究fT（t）的參數估計時，需注意它實際上只有兩個獨立參數。 不妨令 k／σ＝a，／σ＝b，則 fT（t）可以變形為：

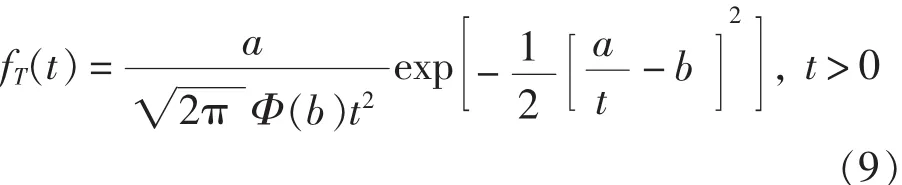
式中，a，b 為參數；Φ（x）為標準正態 N（0，1）的分布函數。這樣在新的電子設備失效分布中就只有兩個獨立參數，這是由fT（t）本身函數特性所決定的。從推導過程看，k，σ，都是相互獨立的參數，但在推導結果fT（t）中，三個參數合并為兩個參數，若要估計出σ，須事另外作出k的估計，以下只對式（9）做出參數 a，b的估計。

首先考慮矩估計，對于一般的矩估計E（tj），j＝1，2，…，由于 fT（t）函數本身特性，積分不能直接求出。針對fT（t）函數的特點，采用負指數矩估計E（t－j）， j＝1，2，…，可以較好地解決估計問題。

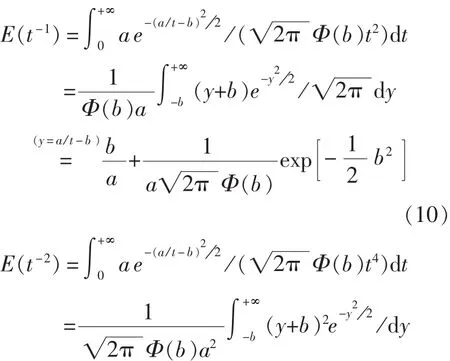
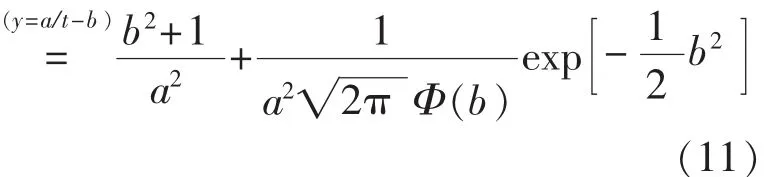
設t1，…，tn為n個電子設備的壽命時間的i.i.d數據，仍然用樣本矩去估計母體矩，所不同在于矩的階數為負數，由方程組：

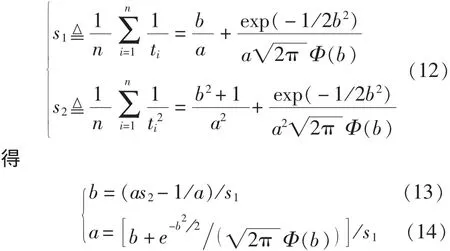
實際計算可將式（13）代入式（14），用對分法求出a的估計a^，再代入式（14）即可求出b的估計b^。不難驗證，本文提出的電子設備失效分布參數的負指數矩估計和其極大似然估計是一致的。

4 新分布下電子設備的可靠性指標

可靠度R（t）描述電子設備在規定條件下和規定時間內完成規定功能的概率，以T表示電子設備使用時間，t為任意實數，則 R（t）=P｛T ＞t｝，根據上文推導的新電子設備失效分布，不難得出：

累積失效概率F（t），即電子設備失效分布的分布函數，表示該類電子設備在規定條件下和規定時間內失效的概率：

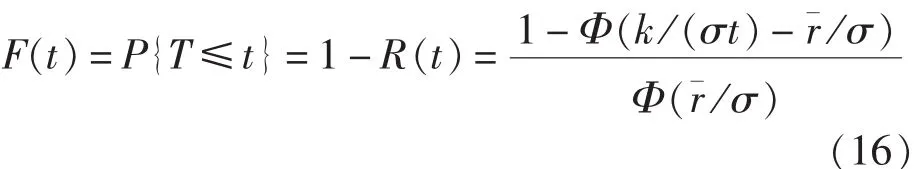
失效密度函數fT（t）表示該類電子設備在t時刻的單位時間內的失效概率。f（t）=F′（t）如式（9）。 平均失效函數 λ（t）：電子設備在 t時刻后的時間內失效的產品數相對于t時刻還在工作的產品數的比值。記r（t）表示t時刻失效設備數，N為樣品總數，則

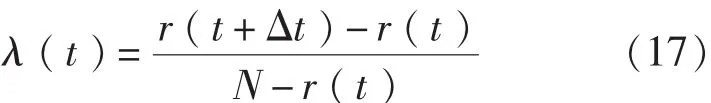
平均故障間隔時間MTBF，即電子設備 （壽命）失效數學期望。由于推導的電子設備失效分布的函數特性，其數學期望不便于求出，根據矩估計的性質，可以利用其一階負指數矩的導數來估計：

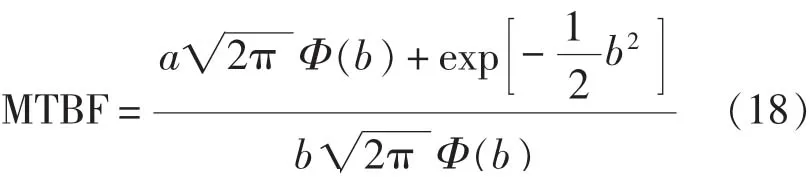
有了電子設備的可靠性指標，就可以進行各個電子模型的可靠性分析，從而可以分析和評價整個系統的可靠性。

5 實證分析

這里選取某電子設備失效的時間數據，該電子設備的最大壽命是1 000 h左右，故障發生平均時間間隔20多小時，下面根據推導利用觀測數據具體分析其可靠性情況。通過統計數據分布情況做失效數統計如圖1所示。從圖1中可以看出失效率隨著時間的增長是逐漸增大的，而指數分布只適用于失效率為常數情形時壽命統計分布，故這里不適合用指數分布做分析。作該電子設備失效統計情況的直方圖如圖2。計算樣本數據的最大方差 K^max＝9.01，得參數估計值 a^＝4.10，b^＝0.21，相應地得分布參數值 r^＝0.45，σ^2＝ 4.81。 作該電子設備失效分布密度函數曲線如圖2中的連續曲線。從中可以看出，該密度曲線類似截斷正態密度曲線，只有一個峰值，它的左極限趨向于原點，右側水平漸近線是時間t軸，符合前面對該概率密度曲線特征的分析。

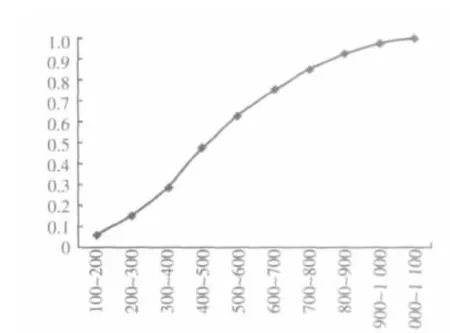
圖1 某電子設備失效率統計

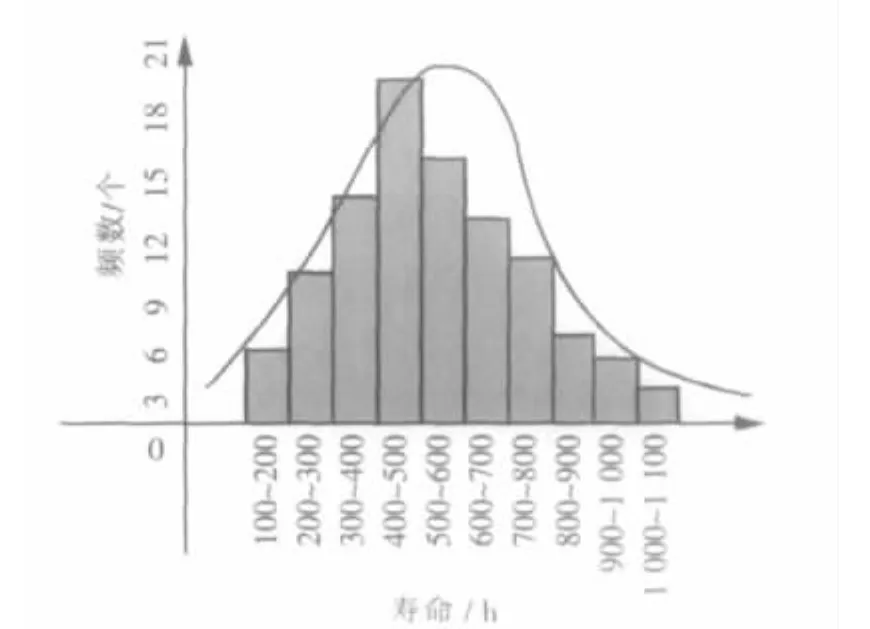
圖2 某電子設備失效分布密度曲線

計算該電子可靠性指標平均故障間隔的時間MTBF≈23，即該電子設備平均故障時間間隔大約是23 h，與實際情況比較符合，說明推導是切實可用的。

6 結束語

本文在電子設備壽命方差在一小段時間內隨時間線性變化的假設下，給出了一種新的電子設備失效分布，對于分布的密度函數性質、參數估計及新分布下電子設備的可靠性指標的計算都做了詳細的推導，并利用某一電子設備失效的時間數據進行實證分析。選取的該電子設備失效率隨時間的增長而增大，故符合本文推導的新分布的情況。實證分析結果也與實際情況基本符合，說明本文推導的新分布及相應的密度函數性質、參數估計方法以及可靠性指數的計算等，都是切實可行可用的。這就為電子設備可靠性的分析提供了新的理論指導及操作方法，有利于開展電子設備可靠性的進一步研究。

［1］ 李永紅.電子系統設備可靠性預計與評估標準及其指南淺析［J］.航空標準化與質量，2006（2）：50-54.

［2］ 伏洪勇，林寶軍，陳福恩.一種基于通用失效率的航天設備可靠性評估算法［J］.空間科學學報，2007，27（3）：250-252.

［3］ M ACIEJEWSKI H，ANDERS G.Estimation of impact of maintenance policies on equipment risk of failure ［C］//IEEE Computer Society Washington，DC，USA，2006：351-357.

［4］ 白宏光，葛紅宇.電子設備的可靠性統計試驗方法研究［J］.電子產品可靠性與環境試驗，2008，26（3）：40-43.

［5］ 王志剛，戴柏林.電子設備可靠性試驗技術的應用與發展［J］.環境技術，2008，2（1）：25～29.

［6］ 朱忠義，常青美.電子設備的可靠性分析與預測［J］.光盤技術，2007（4）：51-53.

［7］ 童恒慶.理論計量經濟學［M］.北京：高等教育出版社，2008.

［8］ 蘇振中，羅錦，江勁勇.基于可靠性仿真的電子設備故障規律建模［J］.計算機測量與控制，2007，15（1）：29-31.

［9］ EDWAR DS J，OAK H.，CARR L.The impact of variable hazard rates on in-service reliability ［J］.Proceedings of the Institution of Mechanical Engineers，Part E.Journal of Process Mechanical Engineering，2001，215（3）：233-242.

［10］ CHENG G，LIG，CAIY.Reliability-based structural optimization under hazard loads ［J］.Structural and Multidisciplinary Optimization，2005，16（2）：128-135.

New Approach to Electronic Equipment Failure Distribution of Naval Vessels

Liu Hui Li Lei
China Ship Developmentand Design Center， Wuhan 430064， China

With t he application of state-of-the-art electronic equipment in naval vessels， it requires more robust and reliable performance in response to increasing demand on the technical property and system structure.For this reason， a new approach to failure distribution of electronic equipment wa s derived given that the life-cycle variance of equipment in actual use environment varie d linearly.Additionally， function＇s parameter characteristics of distribution density were examined and an estimation of parameters negative exponentialmoment in the case of complete data wa s performed.Consequently， the reliability indexes of electronic equipment for the new failure distribution were deduced.Empirical analysis wa s also carried outand it demonstrate d that the failure probability of the equipment become greaterwith the increase of time.The results agree with the actual case as a whole and comply with the derivation of new failure distribution.

reliabil ity； failure distribution； negative exponentialmoment； estimation

U665

A

1673-3185（2010）03-63-04

10.3969/j.issn.1673-3185.2010.03.015

2009-07-06

××艦全壽期綜合保障技術應用研究（Z0820092001）

劉 會（1980-），男，碩士，工程師。研究方向：艦載作戰系統。E-mail：44552833@qq.com

李 蕾（1963-），女，研究員。研究方向：艦載作戰系統