考慮估計方差的軟件可靠性估計

劉舒辰 孫莉

1南京理工大學計算機科學與技術學院 江蘇 210094 2鹽城工學院信息工程學院 江蘇 224003

0 引言

軟件可靠性是描述和評價軟件質量屬性的一個特征量。可表示為：在規定的條件下和規定的時間內，軟件成功地完成規定功能的能力或不引起系統故障的能力，稱其為軟件可靠性。到目前為止，軟件可靠性的定量度量方法還很不完善，并且基本沿襲硬件可靠性度量指標化概念。然而近年來，軟件可靠性的評估特征量越來越受到重視，并且已取得可喜的進展。國外已相繼研究出多種靜態和動態模型及相關的計算方法，來評估軟件的可靠性。例如，用可靠性增長測試模型定量地評估軟件可靠性，用靜態模型在測試之前評估軟件可靠性等。

由于軟件市場的競爭，現代軟件系統的設計需要日益縮短的開發時間和精簡的測試預算。雖然系統設計者和用戶對軟件系統的要求是高可靠性和低風險，但是對軟件組件可靠性進行非常精確的測量通常并不可行。通常采用的方法是對軟件組件可靠性進行估計，而可靠性工程師一般會忽略估計方差。如果估計方差非常大的時候，這種假設會產生誤導作用。為了獲得低風險的系統設計，我們必須明確的考慮可靠性估計方差。

為了滿足這些開發需求，軟件系統需要有效利用系統可靠性模型和改進技術，如可靠性優化模型和權重度量。因此，在現實世界對組件可靠性估計的限制條件下，我們必須把系統可靠性模型技術和度量不可靠的統計觀點結合，才能開發出真正有用的可靠性估計模型和優化算法。

本文首先分析現有的軟件組件可靠性估計的參數模型，其次在基于組件可靠性估計不可靠的特點上，提出一種系統可靠性估計的非參數模型。

1 國內外研究現狀

目前，軟件可靠性工程是一門雖然得到普遍承認，但還處于不成熟的正在發展確立階段的新興工程學科。

國外從上世紀 60年代后期開始加強軟件可靠性的研究工作，經過 20年左右的研究推出了各種可靠性模型和預測方法，于1990年前后形成較為系統的軟件可靠性工程體系。西歐各國每年都有大量人力物力投入軟件可靠性研究項目，并取得一定成果。

國內對于軟件可靠性的研究工作起步較晚，在軟件可靠性量化理論、度量標準(指標體系)、建模技術、設計方法、測試技術等方面與國外差距較大。國內多數軟件的生產方式還處于計算機時代的早期階段，缺點很明顯，主要表現在：①透明度差；②軟件交付系統聯調前只靠自檢，質量得不到保證；③用戶對交付的軟件可靠性缺乏信心。

當前系統可靠性估計的方法有兩類：參數模型和非參數模型。參數模型是假設系統和組件的失效時間有一個確定的分布。如果軟件生命周期的分布是未知的，或者根據有限的失效數據或短暫的生命期計劃難以推斷出生命周期的分布，則這種模型就不適用。非參數模型不需要關于生命周期分布的任何假設，也不需要知道組件失效時間的分布。當組件失效時間難以記錄或對于可靠性極高的產品，僅用少量的失效數據去定義合適的失效時間分布的情況下，該模型則非常實用。現在的理論研究主要都集中在系統可靠性估計的參數模型。

2 軟件可靠性估計的非參數模型

確定組件可靠性估計及可靠性估計方差有很多方法。常用的方法是把失效部件的數量看成是二項式變量，組件可靠性就成為了分布參數。如果系統中使用的第i個部件，分配了ni個部件參加測試。每個組件測試t小時，在測試時間內觀察到 ki個錯誤(ki≤ ni)。每個組件的狀態(有效/失效)被看作一個獨立的具有參數 ri(t)的柏努利試驗，ri(t)是在任務時間 t時的可靠性。

軟件系統可靠性估計的各種非參數模型中，除了擴展對數正態模型ELN和修正最大似然模型MML，其它所有模型都需要系統組件的可靠性估計是統計獨立的。因此，為了克服傳統的非參數估計模型的缺點，我們提出了一個新的可靠性估計模型的非參數模型：遺傳函數GF模型。這種新模型不僅可以擴充現有的可靠性估計理論，解決了原來的非參數模型不適用于具有統計獨立的組件可靠性估計的問題；而且也適用于具有任意重復組件的系統。當重復的組件在系統中任意的使用時，新模型為系統可靠性估計的期望值和方差提供了精確的估計。

2.1 遺傳函數GF模型

開始，系統可靠性R表示成子系統不可靠性Qi(i=1,2, ...s;s為子系統的個數)的函數；同時，子系統不可靠性 Qi和組件不可靠性 qh(h=1,2,...c;c為組件類型的數目)之間的相應關系也可以建立。這樣通過升序排列組件不可靠性估計值hq^，可以計算系統可靠性估計的方差 Var(R)和可靠性的無偏估計R^的期望值。最后，可以獲得R^的置信區間。

該模型開發程序如圖1所示。

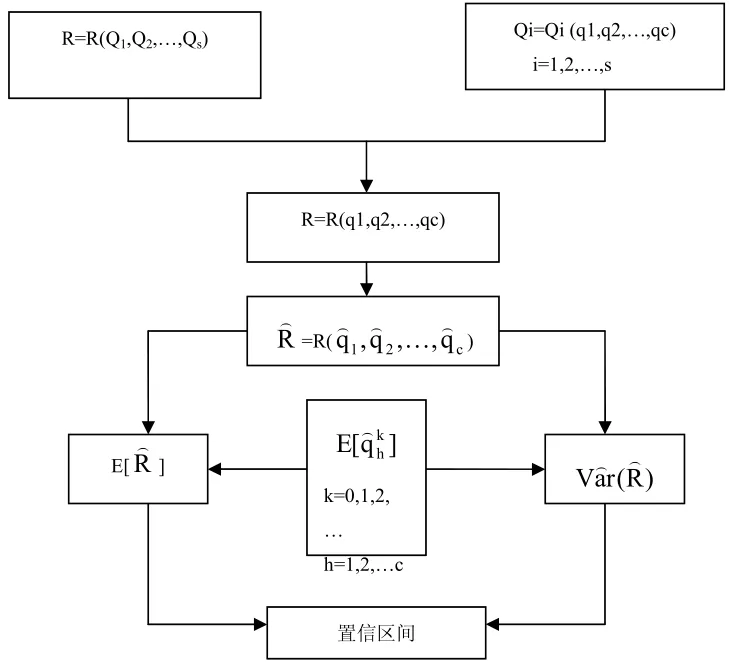
圖1 遺傳函數GF模型開發程序

2.2 系統可靠性的近似值

系統可靠性一般可以表示成組件可靠性的函數：

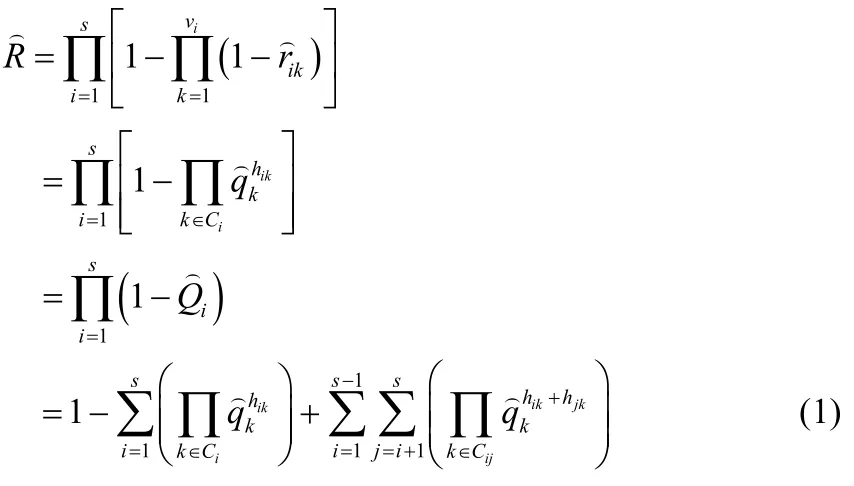
這里：s=子系統的個數

vi=子系統i中組件的個數，i=1，2，...，s

=子系統i的不可靠性，

Ci=子系統i中使用的所有類型的組件集合，Cij= Ci∪Cj

上式清楚的建立起系統可靠性的估計值和組件不可靠性估計值之間的關系。

2.3 系統可靠性估計的期望值和方差

每個子系統通過選擇組件形成冗余級別。由于不同的制造技術和質量保證規定，即使同一個子系統中功能相同的組件也會具有不同的可靠性、價格和權重。因為初始測試樣本不夠大，組件的可靠性估計肯定會受估計不可靠的特點的影響。這些不可靠性將會導致系統級的可靠性估計方差的產生。

系統可靠性估計的期望值可以通過直接對(1)式進行期望化：

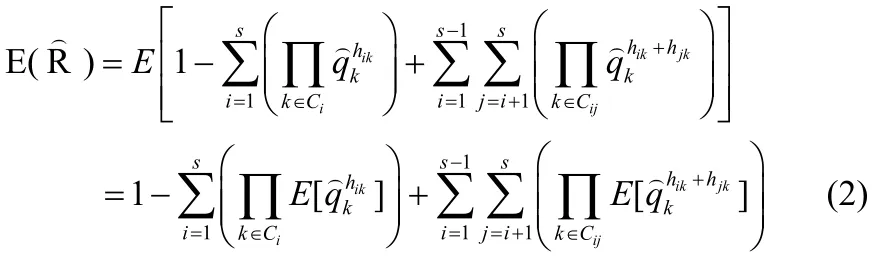
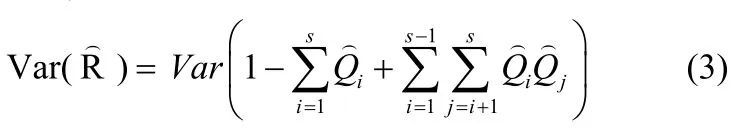
3 結束語

通常，進行可靠性估計的前提條件是：假設組件或系統的生命周期分布可以用參數模型來表示。但是，如果系統或組件對于原始分布的推論沒有充足的失效數據，這個參數模型就不適用了。可靠性工程師一般會忽略估計方差，并且把系統或組件的可靠性看作確定量。如果估計方差非常大的時體防護系統，有組織有計劃地監測和分析終端安全狀態，統一配置終端安全策略，提高政務終端的安全保障能力，確保終端正常、高效地運行。

不過，網絡安全復雜多變，政府辦公網絡終端安全建設除了依靠相應的產品技術外，制度規范也是必不可少的，三分技術，七分管理，政府部門需要從自身入手，制定切實可行的制度來規范員工使用計算機終端的行為，才能更好的杜絕政府辦公網絡的安全隱患。終端安全管理的制度規范條例要反復修改，反復討論，在獲得領導和大多數職工的認可后，正式發布就要認真執行，定期檢查審核，不能只是停留在紙面上當作擺設，關鍵是落實檢查和定期審核，需要有相應的機構和人員專門從事安全制度的落實情況。

[1]柯江源.我國電子政務網絡存在的安全隱患[J].網絡安全技術與應用.2006.

[2]蔡智龍，羅曉哲.淺談電子政務辦公系統中的信息安全問題[J].廣東農工商職業技術學院學報.2007.