基于PCA和PNN的發動機故障診斷研究

李鳳春

山東理工職業學院電氣工程系 山東 272105

0 前言

概率神經網絡(Probabilistic Neural Network，PNN)是在徑向基函數(RBF)神經網絡的基礎上發展而來的一種前饋型神經網絡，最早是由D.F.Specht博士在1989年提出。其實質是基于貝葉斯最小風險準則的一種并行算法，特別適合于模式識別及分類。PNN結構簡單，訓練簡潔，當獲得足夠多且足夠代表性的樣本后可直接使用，無需訓練過程，在一般的模式識別問題中都能取得比較理想的效果。

但PNN在訓練樣本數量較大冗余度較高的情況下，分類效果往往不理想。主成分分析(Principal Component Analysis，PCA)是一種重要的多元統計分析方法，它將顯示變量作一定的線性轉化產生數量較少的隱式變量，降低原始數據空間的維數，再從新的隱式變量中提取主要變化信息及特征，這樣既保留了原有數據信息的特征，又消除變量間的關聯、簡化分析復雜度，從新的數據空間中提取符合相應的主元數，同時也消除了部分的系統噪聲干擾。目前PCA被廣泛用于神經網絡，主要用來降低神經網絡輸入向量的維數，進而提高神經網絡的模式識別效率。為此，本文提出了一種基于PCA和PNN的故障診斷方法，克服了訓練樣本數據冗余度比較大的缺點，并以某汽車發動機的故障診斷為例驗證了所提算法的有效性。

1 主成分分析法

主成分分析法(PCA)通常又稱為Hotelling變換或者K-L變換，它是研究如何將多指標問題轉化為較少綜合指標的一種重要方法，是一種基于目標統計特性的最佳正交變換，這是因為它具有很多重要的優良性質，如變換后產生的新的分量正交或者不相關，以部分新的分量表示原矢量時均方誤差最小，變換矢量更趨確定、能量更趨集中等，這使它在特征選取、數據壓縮等方面都有著極其重要的應用。

設x=(x1,x2,???,xn)T為n維隨機矢量，則PCA的具體計算步驟如下：

（1）將原始觀察數據組成樣本矩陣X，每一列為一個觀察樣本x，每一行代表一維數據。

（2）計算每一維的均值，即計算樣本矩陣X每一行的均值，并對矩陣中的每個樣本x做如下處理：

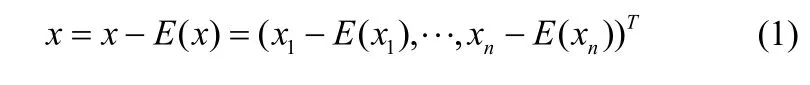
這樣做的目的是簡化利用新生成的分量估計原始目標特征時估計式的形式。

（3）計算樣本的協方差矩陣：

（4）計算協方差矩陣Cn的特征值λi及相應特征向量，其中i=1,2,…,n。

（5）將特征值按由大到小順序排列，并按照下式計算前m個主元的累積貢獻率：

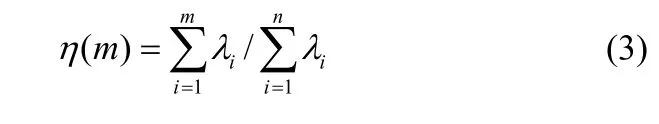
（6）取前m個較大特征值對應的特征向量構成的變化矩陣'T：

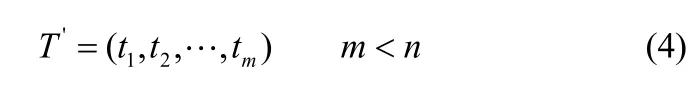
（7）通過Y=(T')TX計算前m個主成分，達到降低維數的目的。

若用壓縮后的數據Y估計原始數據，即數據恢復，可以按照以下步驟進行處理：

（1）估計原始數據矩陣：

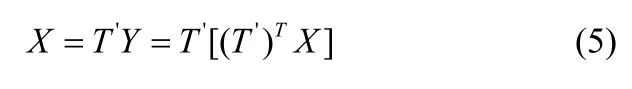
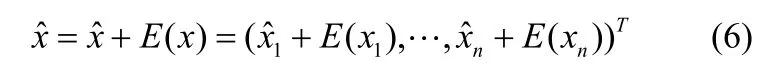
（2）對估計矩陣X每一維分別進行加均值處理：由于變換矩陣'T僅由協方差矩陣的部分特征向量構成，因此，恢復數據不可能完全與原始數據相同，差異程度由所選的m個主元的累積貢獻率衡量。

2 基于PCA和PNN的汽車發動機故障診斷研究

2.1 發動機模型描述

發動機是最常用的動力設備之一，在國民經濟和日常生活中起著舉足輕重的作用，廣泛應用于各個行業，已成為某些行業中不可或缺的關鍵設備。它具有零部件多且相互關聯、運動復雜、工作環境惡劣等特點，因而發生故障的可能性也比較大，而且發生故障后，將會影響機械系統的正常運轉，直接或者間接地造成巨大的經濟損失。發動機在運行過程中，最常見的故障一般分為兩類，一類是油路故障；另一類是氣路故障。這兩類故障的檢測與診斷一直是研究的熱點。

本文以某汽車發動機的故障診斷為研究實例。在發動機運行過程中，選取AI、MA、DI、MD、TR和PR共計6個變量作為特征參數。其中，AI為最大加速度指標，MA為平均加速度指標，DI為最大減速度指標。

在進行故障診斷時，首先根據PCA對所提取的特征參數進行降維處理，然后利用 PNN進行診斷，診斷模型如圖 1所示。

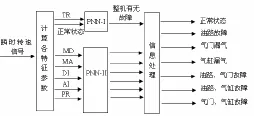
圖1 基于PNN的發動機診斷模型

2.2 仿真研究

由圖2可見，我們設計了兩個PNN進行故障診斷。PNN-I的輸入層有兩個節點，對應TR和正常狀態；樣本模式層有兩個節點，分別對應正常和故障兩種模式；輸出層有兩個節點，分別對應正常和故障兩種狀態。

PNN-II的輸入層有5個節點，分別對應5個特征參數為AI、MA、DI、MD、PR；模式層有十個節點，對應每個節點的正常和故障中的10組模式；輸出層有4個節點，分別對應油路故障、氣門漏氣、汽缸漏氣和正常4種狀態。所謂信息處理就是通過輸出的4種狀態綜合判定實際輸出究竟是單故障還是復合故障。

選用發動機中的1號汽缸進行分析。經過分析，該汽缸一共出現了3種故障，分別為油量少、氣門漏氣和汽缸漏氣，再加上正常狀態，可以認為一共有4種故障模式。利用二進制數格式描述這4種故障模式，如表1所示。這4種故障模式通過現場試驗和對歷史資料的收集分析，可以得到4組故障樣本數據，如表2所示。

表1 故障模式分類

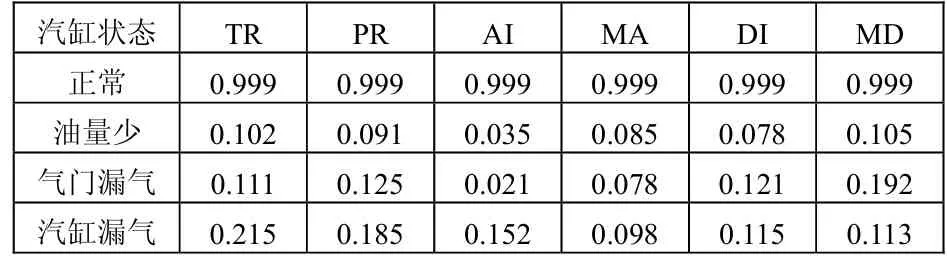
表2 故障樣本數據

由于這些數據之間相差都不大，因此，不需要再進行歸一化處理。將表2所得的故障樣本數據用PCA方法進行分析處理，得到降維后的數據，如表3所示。

表3 降維后的故障樣本數據

利用這些降維后的故障信息作為網絡的訓練樣本，從而創建一個概率神經網絡用于故障診斷。PNN的創建方法和RBF網絡的創建方法非常相似，代碼為：

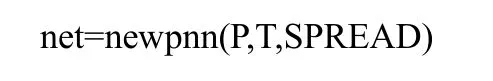
其中，P和T分別為輸入向量和目標向量，SPREAD為徑向基函數的分布密度，默認為 0.1。為了更好地分析SPREAD對網絡性能的影響，這里將SPREAD設置為5個值，分別為0.1、0.2、0.3、0.4和0.5。

函數 newpnn已經創建了一個準確的概率神經網絡，可以利用該網絡進行故障診斷和分析了。

首先，檢驗網絡對訓練數據的分類：

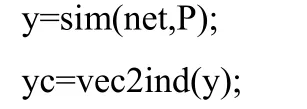
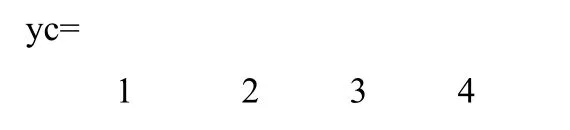
不同的 SPREAD值對應的概率神經網絡的輸出結果都是一樣的，即：由此可見，網絡成功地將故障模式分為了4類。為了進一步檢驗網絡的分類效果，接下來給出了一組測試樣本數據，如表4所示。這組數據都來源于真實的故障信息，因此可以有效地檢驗網絡的分類性能。

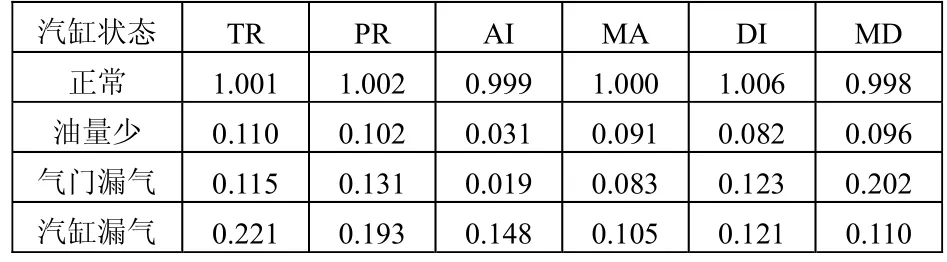
表4 測試樣本數據

同樣的，根據PCA方法對表4所得的測試樣本數據進行分析處理，并得到降維后的數據，如表5所示。

表5 降維后的測試樣本數據

利用表5降維后中測試樣本對概率神經網絡進行測試，代碼為：

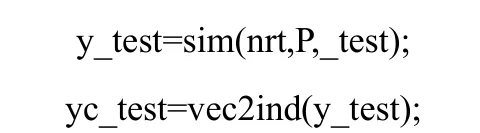
輸出結果為：

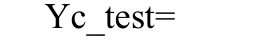
由此可見，網絡的分類是正確的。也就是說，概率神經網絡成功地診斷出了這4種故障。

3 結語

本文提出了一種基于PCA和PNN的汽車發動機的故障檢測與診斷算法。仿真研究結果表明，與傳統的PNN相比，該方法在降低數據維數的同時保證了很高的識別正確率，進一步說明了PCA很好地保留了原始特征信息。在保證較高的分類識別率的前提下，簡化了識別算法、提高了識別算法的推廣能力和運算速度，這對于分類識別系統尤其是實時分類識別系統具有重要意義。

[1] Specht D F.Probabilistic neural network [J].Neural Network.1990.

[2] 李冬輝,劉浩.基于概率神經網絡的故障診斷方法及應用[J].系統工程與電子技術.2004.

[3] 常羽彤,張鵬.基于 PNN 的飛機發動機故障診斷研究[J].微計算機信息.2007.

[4] 邢杰,蕭德云.基于 PCA 的概率神經網絡結構優化[J].清華大學學報(自然科學版).2008.

[5] 李軍梅,胡以華,陶小紅.基于主成分分析與 BP神經網絡的識別方法研究[J].紅外與激光工程.2005.

[6] 楊榮英,苗張木.BP神經網絡主成分分析法在交通需求預測中的應用[J].武漢理工大學學報.2002.

[7] 黃孝彬,劉吉臻,牛玉廣.主元分析方法在火電廠鍋爐過程檢測中的應用[J].動力工程.2004.

[8] 孫文爽,陳蘭祥.多元統計分析[M].北京:高等教育出版社.1994.