制導炸彈連續打擊下混凝土重力壩的破壞效應*
李本平
(第二炮兵指揮學院,湖北 武漢 430012)
1 引 言
未來戰爭中,對重要軍事、民用設施等戰略目標實施多波次重復打擊已成為必然,多彈頭分導技術使得重復打擊具有很強的實戰性[1]。在戰術上,重復打擊分為2個方面:(1)以分布式多彈同時爆炸方式攻擊重要的點目標或面目標;(2)重復連續打擊。連續打擊的實質就是彈藥爆炸相繼作用。關于多彈爆炸相繼作用破壞效應研究,主要集中在空中多點聚集爆炸、淺水中多點爆炸、爆炸應力波相互作用的動態光彈性以及鉆地彈聚集爆炸效應[2-3]等方面。研究制導炸彈連續打擊下混凝土重力壩的破壞效應,可以為大壩的安全評估以及綜合防護提供理論依據和支撐,具有十分重要的軍事價值和現實意義[4]。
本文中選取某制導炸彈作為研究對象,通過對大口徑、高彈重武器的侵徹爆炸的全過程進行3維數值仿真,探討2枚制導炸彈跟進打擊作用下混凝土重力壩的破壞效應。
2 計算模型
選取的研究對象為混凝土重力壩,由泄洪壩段、兩岸廠房壩段、升船機壩段、兩岸非溢流壩段4部分組成。根據壩段的地理位置及重要性,選取泄洪壩段作為計算分析對象。
泄洪壩段高185 m,長483 m,分23個壩段,每個壩段長21 m,壩頂寬40 m。在2個壩段之間布置凈寬8 m的泄洪表孔,表孔底部距壩頂25 m。由于每個壩段彼此獨立,之間為施工縫,計算時,選取1個壩段進行計算。由于泄洪壩段體積龐大,考慮到目前制導炸彈的侵徹深度和彈藥量,制導炸彈侵徹爆炸僅對泄洪壩段產生局部破壞效應,對壩體整體穩定不會構成任何威脅。因此,不考慮壩基的穩定以及壩體與地基間的相互作用。另外,壩后庫水水位一般比壩前水位低得多,而且對壩體的穩定是有利的,按最不利原則,建立計算模型時不考慮壩后庫水。鑒于此,選取大壩計算模型如圖1所示。大壩底部采用約束邊界和無反射邊界。計算水域為壩前10 m,深度為10 m。由于大壩高度比厚度大得多,從目前精確制導炸彈的侵徹深度看,盡管從壩頂豎直入射的概率高,但水平入射跟進打擊相比垂直入射跟進打擊的危害相應要嚴重得多。因此,本文中考慮尺寸和裝藥量完全相同的2枚制導炸彈均從大壩下游水平入射,撞擊點位于大壩下游垂直段的中心,撞擊速度v=240 m/s。一般來說,制導炸彈跟進襲擊相隔一定時間,相隔時間與數值模擬的計算時間相比近似無限大,因此,計算時假設相隔時間很短,在首枚制導炸彈爆炸大壩響應結束后第2枚制導炸彈跟進侵徹,這樣,相隔時間的長短對計算結果沒有影響。除和壩體接觸面以及自由水面外,庫水模型其他4個面均采用無反射邊界。由于侵徹計算對單元網格精度要求加高,因此,制導炸彈侵徹作用一定范圍單元網格加密,即模型中壩體垂直段中部厚度為1 m的范圍進行單元網格加密處理。大壩和彈體劃分Lagrange網格,壩前庫水和彈藥采用ALE網格,模型節點共154 480個,3維實體單元共142 220個,如圖2所示。

圖1 大壩計算模型Fig.1 A calculation model for the dam
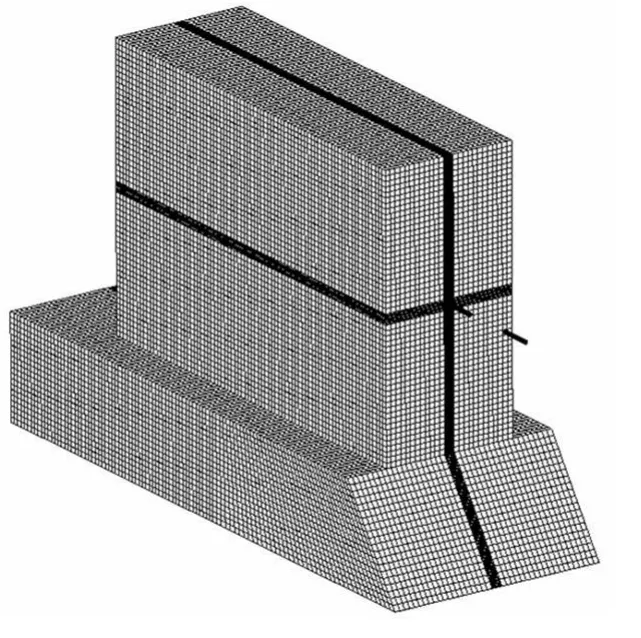
圖2 模型網格Fig.2 Mesh of the model
3 材料模型及計算參數
3.1 大壩材料本構模型
大壩材料為碾壓混凝土,采用塑性隨動硬化材料來模擬碾壓混凝土。這種材料屬于各向同性應變率相關塑性材料中的塑性隨動材料,并且含有失效應變[5]

式中:σy為硬化屈服應力;σ0為初始屈服應力;β為硬化參數,0≤β≤1;Ep為塑性硬化模量為有效塑性應變;k為屈服應力縮比系數,k=1+(˙ε/C)1/P,C、P為應變率參數。大壩材料的計算參數:密度,2.4 t/m3;動態彈性模量,30.0 GPa;泊松比,0.2;屈服強度,24 MPa;硬化參數β,1;切線模量,7.0 GPa;應變率參數C,25;應變率參數P,1.5;失效應變εp,0.002;動態抗拉強度,6.0 MPa。
3.2 爆轟產物狀態方程
制導炸彈裝藥Q=306 kg[6]。高能炸藥起爆后炸藥單元體內的壓力由狀態方程求得,Jones-Wilkens-Lee狀態方程表示為

式中:A、B、R1、R2、ω是材料常數,p是壓力,V是相對體積,E0是初始比內能。
炸藥的計算參數:密度,1 670 kg/m3;爆速,7 km/s;A,371 GPa;B,3.223 GPa;R1,4.2;R2,0.95;ω,0.3;E0,7.0 GPa。
3.3 水的狀態方程
水作為1種流體,采用Grüneisen狀態方程[7],計算參數:密度,998.21 kg/m3;C,1647;S1,1.921;S2,-0.096;S3,0.0;γ0,0.35;A,3.0;E0,2.895;ν0,1.0 。
3.4 彈體模型及計算參數
某制導炸彈質量m=2130 kg,彈長L=5.84 m,炸彈直徑d=370 mm,裝藥Q=306 kg,彈殼厚度δ=1 cm,彈殼為鎢合金材料,彈頭按剛體處理。彈殼材料計算參數[8]:密度,7 896 kg/m3;動態彈性模量,350 GPa;泊松比,0.3;屈服強度,815 MPa;硬化參數β,1;切線模量,21.0 GPa;應變率參數C,40;應變率參數P,5;失效應變εp,0.08;動態抗拉強度,1 350 MPa。
4 計算結果與分析
4.1 振 速
選取壩頂中心節點,整理得出水平方向和豎直方向振動速度時程曲線如圖3所示。由圖可見:侵徹引起的振動很小,引起質點振動的主要是彈藥的爆炸。曲線上有2個明顯的波峰,第2枚制導炸彈爆炸時,首枚制導炸彈爆炸引起的大壩響應已很小,說明計算所取的2枚制導炸彈襲擊時間間隔是可行的。第2枚制導炸彈彈藥中心基本上在該節點正下方,因此引起該節點處垂直向振速峰值比首枚制導炸彈爆炸的大,達15.51 cm/s。

圖3 振動速度時程曲線Fig.3 Vibration velocity against time
4.2 應力云圖
圖4是壩體應力變化云圖,由圖可以看出:制導炸彈在侵徹過程中,僅在撞擊點附近區域的壩體中產生應力集中現象(圖4(a)、圖4(c)),說明制導炸彈的侵徹僅引起壩體局部沖擊破壞。制導炸彈彈藥爆炸對壩體的破壞作用范圍則相應要大得多,從應力等值線的范圍看,爆炸的破壞作用在垂直侵徹方向比平行侵徹方向的大(圖4(b))。t=85 ms時,第2枚制導炸彈開始侵徹壩體,從應力云圖(圖4(c))看,除撞擊點附近區域產生應力集中外,壩體其他部位應力近似為零,說明第2枚制導炸彈開始侵徹壩體時,首枚制導炸彈爆炸使壩體產生的應力基本上已消散,本文中對2枚制導炸彈打擊的時間間隔的設定是合理的。

圖4 大壩第1主應力變化云圖Fig.4 Cloud atlas of the maximum principal stress for the dam
4.3 破壞范圍
圖5是大壩破壞范圍變化圖,圖6是大壩模型對稱面(即大壩軸線方向中心處剖面)破壞范圍圖。由圖可以看出:首枚制導炸彈爆炸壩體破壞范圍在平行彈軸方向約為9 m,垂直彈軸方向約為16 m;由于首枚制導炸彈爆炸形成的“臨空面”的影響,第2枚制導炸彈爆炸壩體破壞范圍在平行彈軸方向約為12 m,垂直彈軸方向約為16 m。2枚制導炸彈爆炸后形成的破壞范圍基本上互相連通。
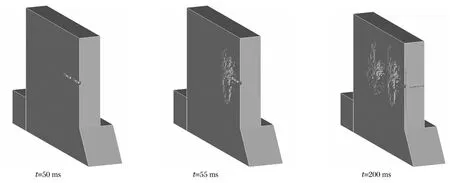
圖5 不同時刻大壩的破壞范圍Fig.5 Damaged range of the dam at different times

圖6 破壞范圍剖面圖Fig.6 Damaged range profile at t=200 ms
5 結 論
通過以上數值模擬和計算成果分析,可以得到以下一些基本結論:
(1)對大口徑、高彈重武器的侵徹爆炸全過程3維數值仿真,可以避免因忽略侵徹過程而直接將炸藥埋設在預定位置的傳統分析方法帶來的誤差,能更加真實地反映制導炸彈的侵徹爆炸破壞作用。通過對相繼打擊武器設置合理間距的簡化處理,可以解決由于相繼打擊間隔時間相對于計算時間過長而帶來計算無法實現的難題。
(2)侵徹引起的振動很小,引起質點振動的主要是彈藥的爆炸。由于相繼打擊間隔時間已遠超過大壩動態響應時間,相繼打擊引起的壩體振動基本上不存在疊加效應。
(3)前枚制導炸彈侵徹爆炸的破壞效應為后繼制導炸彈提供了“臨空面”,使得后繼制導炸彈爆炸破壞效應有所增大。連續打擊下,爆炸后形成的破壞范圍基本上互相連通,對大壩的安全構成威脅。
[1] 李本平.精確制導武器打擊下混凝土重力壩毀傷效應研究[D].武漢:武漢大學,2006:1-2.
[2] 孫百連,顧文彬,蔣建平,等.淺層水中沉底的兩個裝藥爆炸的數值模擬研究[J].爆炸與沖擊,2003,23(5):460-465.
SUN Bai-lian,GU Wen-bin,JIANG Jian-ping,et al.Numerical simulation of explosion shock wave interaction in shallow layer water[J].Explosion and Shock Waves,2003,23(5):460-465.
[3] 鄧國強,周早生,鄭全平.鉆地彈爆炸聚集效應研究現狀及展望[J].解放軍理工大學學報:自然科學版,2002,3(3):45-49.
DENG Guo-qiang,ZHOU Zao-sheng,ZHENG Quan-ping.Study status quo and development of aggregated effect of multipile earth penetration bursts detonated simultaneously[J].Journal of PLA University of Science and Technology:Natural Science Edition,2002,3(3):45-49.
[4] 李本平,黃志鵬.制導炸彈水中爆炸對大壩破壞效應研究[J].防護工程,2008,30(1):13-14.
LI Ben-ping,HUANG Zhi-peng.Study on the damage effect for explosion of precision guided bomb under reservoir water[J].Protective Engineering,2008,30(1):13-14.
[5] 趙海鷗.LS-DYNA動力分析指南[M].北京:兵器工業出版社,2003:25-26.
[6] 張殿臣,王振宇.打擊地下工事的國外高技術武器彈藥參考手冊[M].洛陽:總參工程兵科研三所,1998:1-10.
[7] 張振華,朱錫,白雪飛.水下爆炸沖擊波的數值模擬[J].爆炸與沖擊,2004,24(2):182-188.
ZHANG Zhen-hua,ZHU Xi,BAI Xue-fei.The study on numerical simulation of underwater blast wave[J].Explosion and Shock Waves,2004,24(2):182-188.
[8] Cheng X W,Wang L,Wang F C,et al.Simulation on tungsten alloy PE projectile penetration into targets[C]//International Symposium of Young Scholars on Mechanics and Material Engineering for Science and Experiments.New York:Science Press New York Ltd,2001:367-370.

